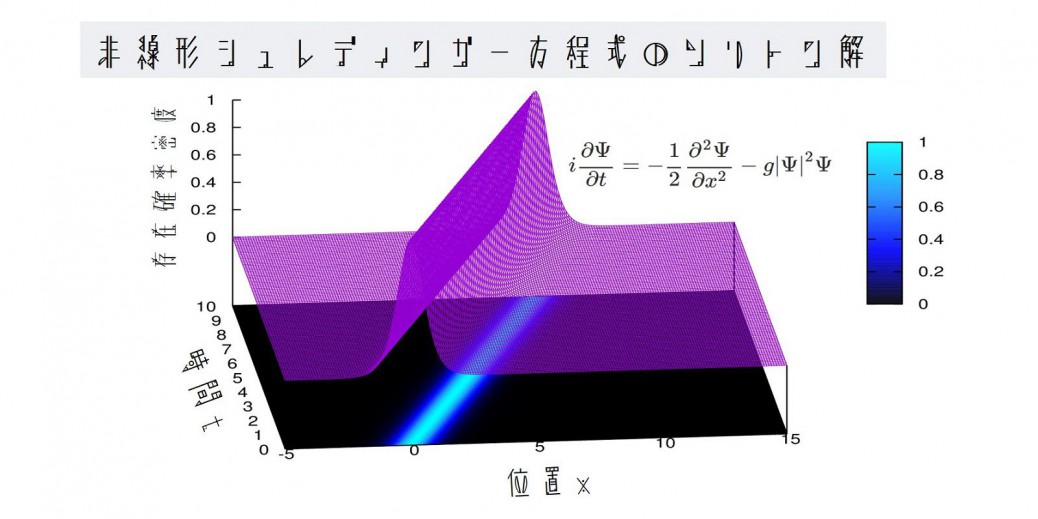
set xr[-5:5]
set yr[-5:5]
set zr[-2.8:2.8]
set view equal xyz
set view 90, 90, 2.5,1
set ticslevel 0
set parametric
set ur[0:1]
set vr[0:1]
set samples 40
set isosamples 10,27
unset xtics
unset ytics
unset ztics
unset key
set palette defined ( 0 '#d0e7ed',1 '#79f0f6')
unset colorbox
rx0=4e0
ry0=5e0
slt=0.3e0
slb=0.1e0
pi2=pi*2e0
q4a=1.0e0 # diamond parameter
q4b=0.6e0 # diamond parameter
q4s=0.4e0 # diamond parameter
dqx(q,u)=q*(cos(u)+0.1e0)**3
dqy(q,u)=q*(sin(u))**3
dqz(qs,q,u)=qs*dqx(q,u)
sizeq=0.8e0
theta=2e0*pi/4e0
rotqx(qx,qy,u,n,theta)=cos(n*theta+pi/4)*sizeq*dqx(qx,u)-sin(n*theta+pi/4)*sizeq*dqy(qy,u)
rotqy(qx,qy,u,n,theta)=sin(n*theta+pi/4)*sizeq*dqx(qx,u)+cos(n*theta+pi/4)*sizeq*dqy(qy,u)
xci=-1.e0
yci=0e0
rci=2.5e0
circlex(n,theta,ph,r)=xci+r*cos(n*theta+ph)
circley(n,theta,ph,r)=yci+r*sin(n*theta+ph)
sloped=-0.25e0
constd=-2e0
Nball=12
dox(q,u)=q*(cos(u))**3
doy(q,u)=q*(sin(u))**3
#---
ball0=rci*0.25e0 # initial radious of balls
ball1=rci # rotating radious of balls
#---
rad=0.1e0
outR=ball1+rad/2
inR=ball1-rad/2
# +--- hypotrochoid ----+
# if h=1 --> hypocycloid
hcyc(n,h,t)=(real(n-1)*cos(t)+h*cos(t*real(n-1)))/real(n)
hcys(n,h,t)=(real(n-1)*sin(t)-h*sin(t*real(n-1)))/real(n)
hc3x(n,h,u,v)=hcys(n,h,u)*hcyc(n,h,v)
hc3y(n,h,u,v)=hcys(n,h,u)*hcys(n,h,v)
hc3z(n,h,u)=hcyc(n,h,u)
hhyp=1e0
nhyp=10
vcr=0.2e0
fth(a,x,x0,f0,x1,f1)=( x < x0 ? f0 : (x > x1 ? f1 : (f0-f1)*tanh(a*(real(x)-(x0+x1)*0.5e0))/(tanh(a*(real(x0)-(x0+x1)*0.5e0))-tanh(a*(real(x1)-(x0+x1)*0.5e0)))+(-f0*tanh(a*(real(x1)-(x0+x1)*0.5e0))+f1*tanh(a*(real(x0)-(x0+x1)*0.5e0)))/(tanh(a*(real(x0)-(x0+x1)*0.5e0))-tanh(a*(real(x1)-(x0+x1)*0.5e0)))))
k0=8 # appaer balls
k1=20 # expand balls and circles to outer circle
k2=20 # rotate balls
k3=20 # rotate balls and superimpose line
k4=20 # expand lines to 3 lines
k5=20 # compose lines to center
k6=20 # expansion center hyptrocoid
k7=40 # make and rotate medjed, make and disappear cascade
k8=30 # medjed come to near
j0=k0
j1=k0+k1
j2=k0+k1+k2
j3=k0+k1+k2+k3
j4=k0+k1+k2+k3+k4
j5=k0+k1+k2+k3+k4+k5
j6=k0+k1+k2+k3+k4+k5+k6
j7=k0+k1+k2+k3+k4+k5+k6+k7
j8=k0+k1+k2+k3+k4+k5+k6+k7+k8
#set term gif animate optimize delay 6 size 500,430
#set output 'fgo.gif'
ht=0.1e0
mint=0e0
maxt=ht*j0
do for[j=0:j0]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(ball0-0.8e0,u*pi2)+xci,doy(ball0-0.8e0,u*pi2)+yci,sloped*(dox(ball0-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(ball0-0.8e0,u*pi2)-doy(ball0-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(ball0-0.8e0,u*pi2)+doy(ball0-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(ball0-0.8e0,u*pi2)-doy(ball0-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,ball0),circley(1,u*pi2,0e0,ball0),sloped*circlex(1,u*pi2,0e0,ball0)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,ball0),circley(1,u*pi2,0e0,ball0),sloped*circlex(1,u*pi2,0e0,ball0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+xci,\
0.1e0*cos(u*pi2)+yci, \
(0.1e0*sin(u*pi2)+xci)*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+xci,\
0.1e0*cos(u*pi2)+yci, \
(0.1e0*sin(u*pi2)+xci)*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,pi2*real(i)/Nball,ball0),\
0.1e0*sin(u*pi)*cos(v*pi2)+circley(1,0e0,pi2*real(i)/Nball,ball0), \
0.1e0*cos(u*pi)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,pi2*real(i)/Nball,ball0))*sloped+constd+fth(1e0,t,mint,0e0,maxt,0.3e0) lw 1 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)**1+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)**1+yci,hc3z(nhyp,hhyp,u*pi)**1 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*(j0+1)
maxt=ht*(j1)
inca=10e0
balla=25e0
do for[j=j0+1:j1]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)+xci,doy(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)+yci,sloped*(dox(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)-doy(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)+doy(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2)-doy(fth(inca,t,mint,ball0,maxt,rci)-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,fth(inca,t,mint,ball0,maxt,rci)),circley(1,u*pi2,0e0,fth(inca,t,mint,ball0,maxt,rci)),sloped*circlex(1,u*pi2,0e0,fth(inca,t,mint,ball0,maxt,rci))+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] fth(40e0,t,mint,0e0,maxt,1e0)*rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,fth(inca,t,mint,ball0,maxt,rci)),\
fth(40e0,t,mint,0e0,maxt,1e0)*rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,fth(inca,t,mint,ball0,maxt,rci)),\
(fth(40e0,t,mint,0e0,maxt,1e0)*rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,fth(inca,t,mint,ball0,maxt,rci)))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*xci+fth(balla,t,mint,0e0,maxt,1e0)*circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*yci+fth(balla,t,mint,0e0,maxt,1e0)*circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*xci+fth(balla,t,mint,0e0,maxt,1e0)*circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*xci+fth(balla,t,mint,0e0,maxt,1e0)*circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*yci+fth(balla,t,mint,0e0,maxt,1e0)*circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+fth(balla,t,mint,1e0,maxt,0e0)*xci+fth(balla,t,mint,0e0,maxt,1e0)*circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,pi2*real(i)/Nball,fth(balla,t,mint,ball0,maxt,ball1)),\
0.1e0*sin(u*pi)*cos(v*pi2)+circley(1,0e0,pi2*real(i)/Nball,fth(balla,t,mint,ball0,maxt,ball1)),\
0.1e0*cos(u*pi)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,pi2*real(i)/Nball,fth(balla,t,mint,ball0,maxt,ball1)))*sloped+constd+0.3e0 lw 1 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)**1+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)**1+yci,hc3z(nhyp,hhyp,u*pi)**1 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*(j1+1)
maxt=ht*(j2)
inca=10e0
balla=25e0
do for[j=j1+1:j2]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1),\
0.1e0*sin(u*pi)*cos(v*pi2)+circley(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1),\
0.1e0*cos(u*pi)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1))*sloped+constd+0.3e0 lw 1 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)**1+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)**1+yci,hc3z(nhyp,hhyp,u*pi)**1 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*(j2+1)
maxt=ht*(j3)
inca=10e0
balla=25e0
do for[j=j2+1:j3]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)*fth(2,t,mint,1e0,maxt,0e0)+circlex(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1),\
0.1e0*sin(u*pi)*cos(v*pi2)*fth(2,t,mint,1e0,maxt,0e0)+circley(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1),\
0.1e0*cos(u*pi)*fth(2,t,mint,1e0,maxt,0e0)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(t-ht*(j1+1))**2+pi2*real(i)/Nball,ball1))*sloped+constd+0.3e0 lw 1 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0)+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0)+yci,hc3z(nhyp,hhyp,u*pi)+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0) lt 1 lc rgb "#79f0f6",\
(cos(v*pi2)*(ball1+fth(2,t,mint,0e0,maxt,1e0)*rad*cos(u*pi2)))+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0)+xci,\
(sin(v*pi2)*(ball1+fth(2,t,mint,0e0,maxt,1e0)*rad*cos(u*pi2)))+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0)+yci,\
(sin(u*pi2)*fth(2,t,mint,0e0,maxt,1e0)*rad)+rand(0)*0.15e0*fth(2,t,mint,0e0,maxt,1e0)+(cos(v*pi2)*(ball1+fth(2,t,mint,0e0,maxt,1e0)*rad*cos(u*pi2))+xci)*sloped+constd+0.3e0 lw 2 lt 1 lc rgb "#d0e7ed"
#------------
}
ht=0.1e0
mint=ht*(j3+1)
maxt=ht*(j4)
inca=10e0
balla=25e0
ball2=9e0
do for[j=j3+1:j4]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
(cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0))+rand(0)*0.15e0+xci,\
(sin(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(sin(v*pi2)*(ball2+rad*cos(u*pi2))))+rand(0)*0.15e0+yci,\
fth(20e0,t,mint,1e0,maxt,0e0)*(sin(u*pi2)*rad)+rand(0)*fth(20e0,t,mint,0.15e0,maxt,0.4e0)+((cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)))*sloped+constd+fth(20e0,t,mint,0.5e0,maxt,1.5e0) lw 2 lt 1 lc rgb "#d0e7ed",\
(cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0))+rand(0)*0.15e0+xci,\
(sin(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(sin(v*pi2)*(ball2+rad*cos(u*pi2))))+rand(0)*0.15e0+yci,\
fth(20e0,t,mint,1e0,maxt,0e0)*(sin(u*pi2)*rad)+rand(0)*fth(20e0,t,mint,0.15e0,maxt,0.2e0)+((cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)))*sloped+constd+fth(20e0,t,mint,0.5e0,maxt,0.5e0) lw 2 lt 1 lc rgb "#d0e7ed",\
(cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0))+rand(0)*0.15e0+xci,\
(sin(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(sin(v*pi2)*(ball2+rad*cos(u*pi2))))+rand(0)*0.15e0+yci,\
fth(20e0,t,mint,1e0,maxt,0e0)*(sin(u*pi2)*rad)+rand(0)*fth(20e0,t,mint,0.15e0,maxt,0.2e0)+((cos(v*pi2)*(ball1+rad*cos(u*pi2))*fth(20e0,t,mint,1e0,maxt,0e0)+fth(20e0,t,mint,0e0,maxt,1e0)*(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)))*(fth(20e0,t,mint,sloped,maxt,-sloped))+constd+fth(20e0,t,mint,0.5e0,maxt,3.8e0) lw 2 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)+rand(0)*fth(20e0,t,mint,0.15e0,maxt,0.3e0)+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.15e0+yci,hc3z(nhyp,hhyp,u*pi)+rand(0)*0.15e0 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*(j4+1)
maxt=ht*(j5)
inca=10e0
balla=25e0
ringa=10e0
ball2=9e0
do for[j=j4+1:j5]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
(((0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)+rand(0)*0.15e0+xci))*fth(ringa,t,mint,1e0,maxt,0e0),\
(((sin(v*pi2)*(ball2+rad*cos(u*pi2))))+rand(0)*0.15e0+yci)*fth(ringa,t,mint,1e0,maxt,0e0),\
(rand(0)*0.4e0+(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)*sloped+constd+1.5e0)*fth(ringa,t,mint,1e0,maxt,0e0) lw 2 lt 1 lc rgb "#d0e7ed",\
((0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)+rand(0)*0.15e0+xci)*fth(ringa,t,mint,1e0,maxt,0e0),\
(((sin(v*pi2)*(ball2+rad*cos(u*pi2))))+rand(0)*0.15e0+yci)*fth(ringa,t,mint,1e0,maxt,0e0),\
(rand(0)*0.2e0+(((0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)))*sloped+constd+0.5e0)*fth(ringa,t,mint,1e0,maxt,0e0) lw 2 lt 1 lc rgb "#d0e7ed",\
((0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)+rand(0)*0.15e0+xci)*fth(ringa,t,mint,1e0,maxt,0e0),\
((sin(v*pi2)*(ball2+rad*cos(u*pi2)))+rand(0)*0.15e0+yci)*fth(ringa,t,mint,1e0,maxt,0e0),\
(rand(0)*0.2e0+(0.5e0*(cos(v*pi2)*(ball2+rad*cos(u*pi2)))+2e0)*(-sloped)+constd+3.8e0)*fth(ringa,t,mint,1e0,maxt,0e0) lw 2 lt 1 lc rgb "#d0e7ed",\
hc3x(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.3e0+xci,hc3y(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.15e0+yci,hc3z(nhyp,hhyp,u*pi)+rand(0)*0.15e0 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*(j5+1)
maxt=ht*(j6)
inca=10e0
balla=25e0
ball2=9e0
do for[j=j5+1:j6]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
fth(20e0,t,mint,0.9e0,maxt,10e0)*hc3x(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.3e0+xci,fth(20e0,t,mint,0.9e0,maxt,10e0)*hc3y(nhyp,hhyp,u*pi,v*pi2)+rand(0)*0.15e0+yci,fth(20e0,t,mint,0.9e0,maxt,10e0)*hc3z(nhyp,hhyp,u*pi)+rand(0)*0.15e0 lt 1 lc rgb "#79f0f6"
#------------
}
ht=0.1e0
mint=ht*real(j6+1)
maxt=ht*real(j7)
inca=10e0
balla=25e0
ball2=9e0
vrt=4e0
do for[j=j6+1:j7]{
t=ht*j
ttx=fth(2e0,t,mint,1e0,maxt,0e0)*vrt*(t-ht*j7)
qt=cos(ttx)
rt=sin(ttx)
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0), \
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(fth(5e0,t,mint,1e0,maxt,1e0)*t-ht*(j1+1))+pi2*real(i)/Nball,ball1),\
0.1e0*sin(u*pi)*cos(v*pi2)+circley(1,0e0,(fth(5e0,t,mint,1e0,maxt,1e0)*t-ht*(j1+1))+pi2*real(i)/Nball,ball1),\
0.1e0*cos(u*pi)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(fth(5e0,t,mint,1e0,maxt,1e0)*t-ht*(j1+1))+pi2*real(i)/Nball,ball1))*sloped+constd+0.3e0 lw 1 lt 1 lc rgb "#d0e7ed",\
"medjed3.png" binary filetype=png array=150x218 flip=y dx=0.01e0 dy=0.01e0 rot=90d center=(xci,yci,0) perp = (qt,rt,0) format="%uchar" u 1:2:3 with rgbimage,\
fth(2e0,t,mint,1e0,(maxt+mint)/2,0e0)*0.6e0*cos(v*pi2)/u+xci,fth(2e0,t,mint,1e0,(maxt+mint)/2e0,0e0)*0.6e0*sin(v*pi2)/u+yci,(abs(fth(2e0,t,mint,1e0,(maxt+mint)/2e0,0e0)) >1e-2 ? u*8e0-8e0/2e0+rand(0)*0.5e0 : 1/0) lw 2 lt 1 lc rgb "#79f0f6"
#------------
}
#
ht=0.1e0
mint=ht*(j7+1)
maxt=ht*(j8)
inca=10e0
balla=25e0
ball2=9e0
vrt=4e0
do for[j=j7+1:j8]{
t=ht*j
#------------
splot \
'background.png' binary filetype=png array=800x452 flip=y dx=0.02 dy=0.02 rot=90d center=(-4.9,yci,0) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage,\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),3.1e0+slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),1e0+slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-2.8e0-slt*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
rx0*cos(u*pi+pi/2),ry0*sin(u*pi+pi/2),-0.7e0-slb*rx0*cos(u*pi+pi/2) lw 1 lt 1 lc rgb "#d0e7ed",\
for[i=10:13] sprintf("fort.%d",i) u (rx0*($1*cos(t*vcr)-$2*sin(t*vcr))):(ry0*($1*sin(t*vcr)+$2*cos(t*vcr))):( $1*cos(t*vcr)-$2*sin(t*vcr) < 0 ? ($3+1.4e0+(slt+slb)*0.5e0*(rx0*($1*cos(t*vcr)-$2*sin(t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette ,\
for[i=50:53] sprintf("fort.%d",i) u (rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr))):(ry0*($1*sin(-t*vcr)+$2*cos(-t*vcr))):( $1*cos(-t*vcr)-$2*sin(-t*vcr) < 0 ? ($3-2.4e0-(slt+slb)*0.5e0*(rx0*($1*cos(-t*vcr)-$2*sin(-t*vcr)))) : 1/0 ):4 w l lw 2 lt 1 lc palette,\
dox(rci-0.8e0,u*pi2)+xci,doy(rci-0.8e0,u*pi2)+yci,sloped*(dox(rci-0.8e0,u*pi2)+xci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
(dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci,(dox(rci-0.8e0,u*pi2)+doy(rci-0.8e0,u*pi2))/sqrt(2e0)+yci,sloped*((dox(rci-0.8e0,u*pi2)-doy(rci-0.8e0,u*pi2))/sqrt(2e0)+xci)+constd lt 1 lw 2 lc rgb "#d0e7ed" ,\
circlex(1,u*pi2,0e0,rci),circley(1,u*pi2,0e0,rci),sloped*circlex(1,u*pi2,0e0,rci)+constd lt 1 lw 2 lc rgb "#79f0f6",\
circlex(1,u*pi2,0e0,rci*0.25e0),circley(1,u*pi2,0e0,rci*0.25e0),sloped*circlex(1,u*pi2,0e0,rci*0.25e0)+constd lw 2 lt 1 lc rgb "#79f0f6",\
for[i=0:3] rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci),\
rotqy(q4a,q4b,u*pi2,i,theta)+circley(i,theta,pi/4,rci),\
(rotqx(q4a,q4b,u*pi2,i,theta)+circlex(i,theta,pi/4,rci))*sloped+constd lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi2*real(i)/4,1.7e0),\
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#79f0f6",\
for[i=0:3] 0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
0.1e0*cos(u*pi2)+circley(1,0e0,pi/4+pi2*real(i)/4,1.7e0),\
(0.1e0*sin(u*pi2)+circlex(1,0e0,pi/4+pi2*real(i)/4,1.7e0))*sloped+constd lw 8 lt 1 lc rgb "#d0e7ed",\
for[i=0:11] 0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(1e0*t-ht*(j1+1))+pi2*real(i)/Nball,ball1),\
0.1e0*sin(u*pi)*cos(v*pi2)+circley(1,0e0,(1e0*t-ht*(j1+1))+pi2*real(i)/Nball,ball1),\
0.1e0*cos(u*pi)+(0.1e0*sin(u*pi)*sin(v*pi2)+circlex(1,0e0,(1e0*t-ht*(j1+1))+pi2*real(i)/Nball,ball1))*sloped+constd+0.3e0 lw 1 lt 1 lc rgb "#d0e7ed",\
'medjed3.png' binary filetype=png array=150x218 flip=y dx=fth(10e0,t,mint,0.01e0,maxt,0.18e0) dy=fth(10e0,t,mint,0.01e0,maxt,0.18e0) rot=90d center=(xci+fth(10e0,t,mint,0e0,maxt,4e0),yci,fth(10e0,t,mint,0e0,maxt,-11e0)) perp = (1,0,0) format='%uchar' u 1:2:3 with rgbimage
#------------
}
#set out
#set terminal wxt enhanced