sikino のすべての投稿

gnuplot

gnuplotで点にラベルを付けて出力

2016年3月20日 sikino コメントする

gnuplotで点とその点の値を付けたいとします。
数点だけならば、

set label "moji" at 4,0.2

とやれば点(4,0.2)に”moji”という文章が書かれます。

複数点の場合を考えます。
ここでは、データ”test.d”として、

1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7

を考えます。gnuplot単体でやることはできないと思います。
若干作業しなければなりません。

ファイル”test.plt”を生成し、中に以下の文を書きます。

unset label

!perl -ane 'print "set label sprintf(\"\%6.4f\",$F[1]) at $F[0]-0.05,$F[1]+0.04\n"' test.d > p.plt

load "p.plt"
plot "test.d" pt 7

とすると各点の位置からx軸方向に-0.05, y軸方向に+0.04ずれた位置にその点のy軸の値が出力されます。gnuplot上で上のファイルを読み込むと以下の出力を得ます。

参考文献
Basic statistics with gnuplot

gnuplot

gnuplotである1つの点のみを表示する

2016年3月20日 sikino コメントする

gnuplotで複数行から成るデータの第n行目だけを点としてプロットしたい場合があります。

例えば、全100行から成るデータ(“data.d”)の第17行目だけをプロットしたいとします。
この時、

plot "data.d" every ::17:0:17:0 u 1:2

とすれば、第17行目だけが点としてプロットされます。

その他、例えばデータではなく、ある関数のf(x)のx=5.7の時だけの値をプロットしたい時は

plot sprintf("< echo ''%f %f''", 5.7,f(5.7))

とすればよいです。

例1

データ”test.d”として

1 0.1
2 0.2
3 0.3
4 0.4
5 0.5
6 0.6
7 0.7

を考えます。この時gnuplot上で、

plot "test.d" every ::5:0:5:0 pt 7

と行うと

というグラフが得られます。

例2

sin(5.7)を考えます。gnuplot上で

plot sprintf("< echo ''%f %f''", 5.7,sin(5.7)) pt 7

とすれば

という画像を得ます。都合上同時にsin(x)も出力しています。

参考文献
　複数のデータファイルのある列の差分表示 -計算機は楽し
 gnuplotのコマンドまとめ(ループとかeveryとか) -Linux, Mac, Emacsについての設定、覚え書き

弾道計算

上下幅が一定の時の軌道と、撃ち上げ撃ち下し時の軌道のずれについて

2016年3月19日 sikino コメントする

今まではゼロインする距離を固定した時の比較を行ってきましたが、
通常軌道を見て適正ホップだ、とか決定するかと思います。
この条件ならば上下幅を一定にしなければ適切な比較とは言えないと思ったのでその場合の結果です。

また、山のフィールドで
斜面の下から上に向かって打つとき、
斜面の上から下へ向かって打つとき
の着弾点は上にずれることを示します。

上下幅が一定の時の軌道

弾道の上下の幅を、0.25gのBB弾で0.9Jで射出した時の弾道の上下幅を基準にして重さを変えた時、弾道がどうなるかを計算すると以下の通りになります。
変更するBB弾の重さは販売されているものを基準とし、
0.12g, 0.20g, 0.21g, 0.23g, 0.25g, 0.28g, 0.30g
にしています。
グラフ中の点は0.05秒ごとの位置をプロットしており、図中の上の数本の線は水平距離のみを見た時のものです。

静止画では

のようになります。

飛距離に対して到達速度は0.12g以外ではほとんど変わりません。
30m付近でおおよそ同じ時間に到達していることが分かります。
それ以降は重いほど早く到達し、かつ遠くまで飛んでいることが分かるかと思います。

やはり銃が許す限り、BB弾は重ければ重いほど良い、ということです。

撃ち上げ、撃ち下し時の軌道のずれについて

山のフィールドにおいて、斜面下から上、または上から下に向かって撃つ時、軌道はどう変わるのでしょうか。
答えは、照準よりも上に飛んでいきます。

以下の画像の状況を考えます。

エネルギーは0.90J, 重さは0.25gを考えます。
下から上に向かって打つときの角度を正にとって$+\theta$
上から下に向かって打つときの角度を負にとって$-\theta$と表すことにします。
また、平坦な場所でゼロイン50mで最小の振れ幅になる軌道で比較します。

それぞれの角度$\theta$の向きで射出した後、撃った角度$\theta$で座標を回転させて主観的な視点で見た時にどうなるかを考えます。

すると、以下の結果を得ます。

横軸は水平の距離ではなく、その角度で見た時の相対的な距離です。
$\theta=0$の時とそれぞれの角度の時を比較すると、角度をつける場合はほとんどの場合で上向きにずれることが分かります。
すなわち、角度がある時はシューティングレンジで合わせた照準よりも上に着弾するのです。

何故でしょうか。ちゃんと理由があります。
上向きにでも下向きにでも、角度があって撃つとき、BB弾に掛かる見かけ上の重力が減少します。

なので角度がある時は重力が小さく感じるので、角度が無いところで調節した時よりも上の方に飛んでいくことになります。
なので、山のフィールドで斜面があるときは、若干下方向を、すなわち相手の膝や腰辺りを狙えばいいのです。

テキストエディタ, プログラミングと数値計算

emacs上で再読み込み

2016年2月20日 sikino コメントする

emacs上でファイルを再読み込みしたいとします。
OSはLinux mint17.1です。

例えば、
emacsであるファイルを開いたまま、sedコマンドでファイルをいじると、そのいじったファイルは現在開いているemacsには反映されません。

これを変更してF5キーを押すだけでemacs上で再読み込みができるようにします。

ホームディレクトリに
.emacs
というファイルを作成し、その中に↓

(defun revert-buffer-no-confirm (&optional force-reverting)
"Interactive call to revert-buffer. Ignoring the auto-save
file and not requesting for confirmation. When the current buffer
is modified, the command refuses to revert it, unless you specify
the optional argument: force-reverting to true."
(interactive "P")
;;(message "force-reverting value is %s" force-reverting)
(if (or force-reverting (not (buffer-modified-p)))
(revert-buffer :ignore-auto :noconfirm)
(error "The buffer has been modified")))

;; reload buffer
(global-set-key (kbd "<f5>") 'revert-buffer-no-confirm)

と入力します。これを記述し、もう一度emacsを立ち上げ,sedコマンド等で外部から編集し、F5キーを押せば更新されます。

参考文献

Emacsで現在開いてるバッファを再読込する

プログラミングと数値計算

sedコマンドによるファイルの書き換え

2016年2月20日 sikino コメントする

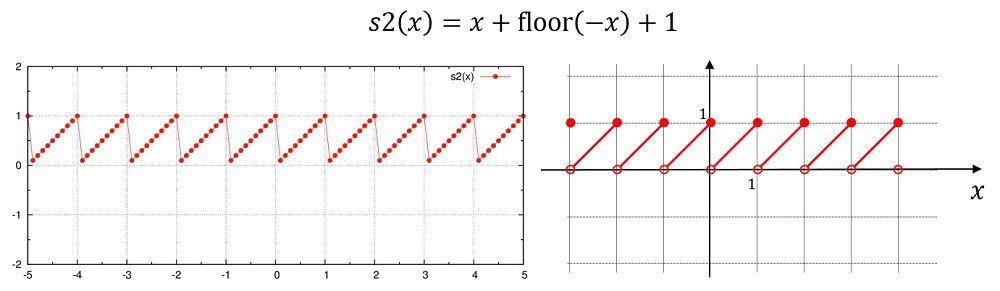
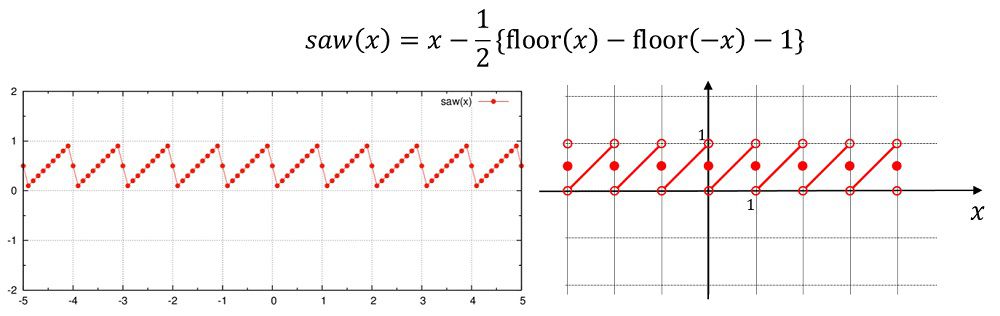
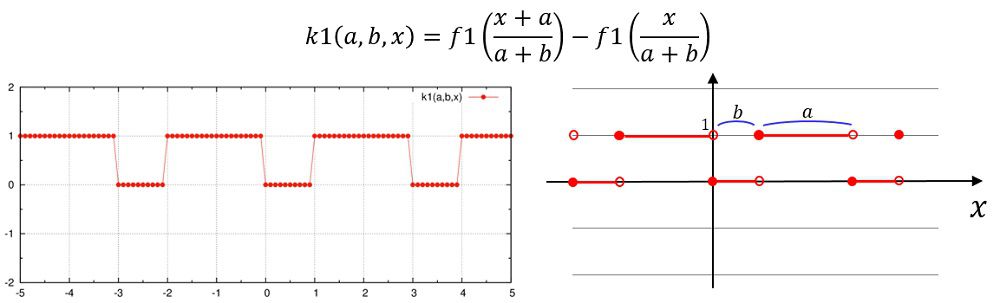
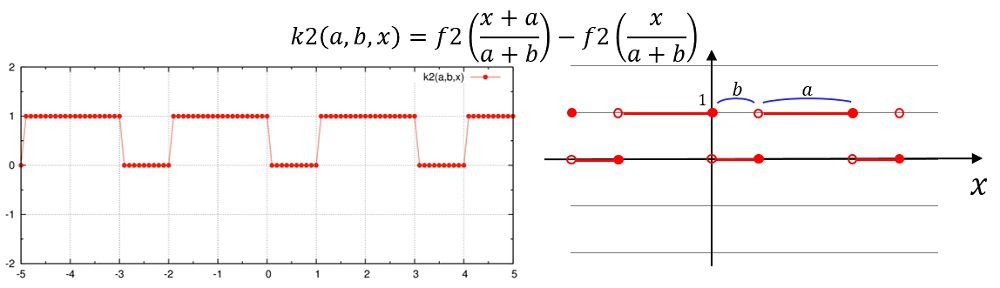
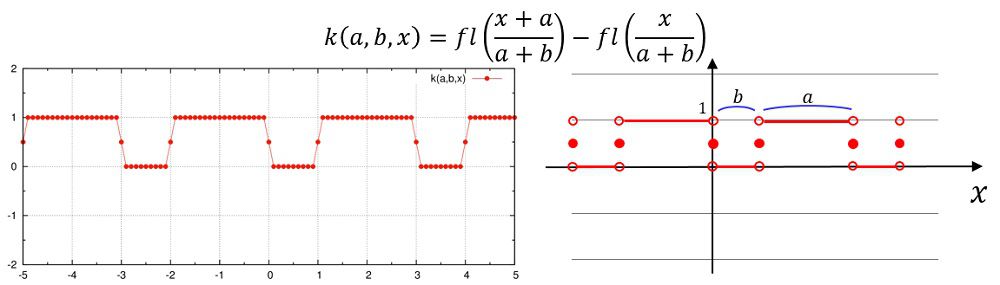
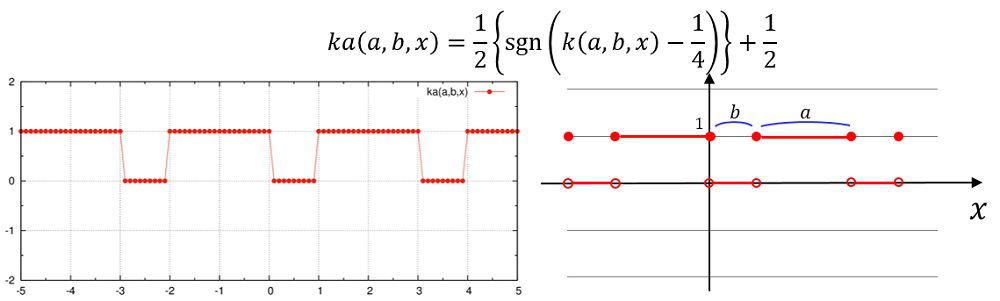
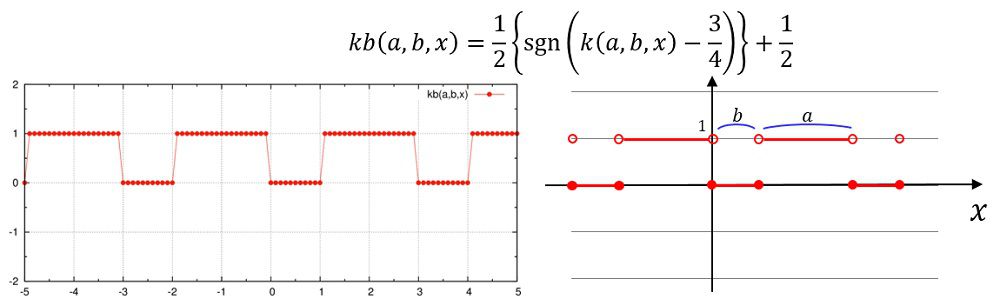
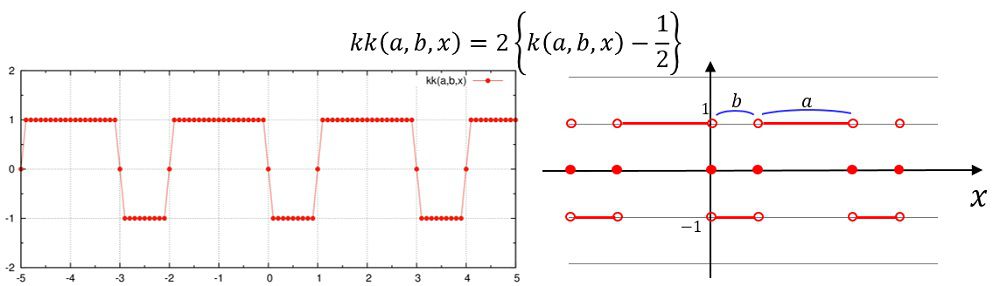
シェルスクリプトによってファイルを書き換えます。

sedコマンドの概要
具体例一覧

sedコマンドの概要

対象とするファイル名”input.ini”の中身に

&input
a=7,
b=13,
c='./dat/',
&end

という文が書いてあるとします。
これのファイルの中身を端末からのコマンドで書き換えるためにはsedコマンドを利用します。

sedコマンドとは、置換用のコマンドです。
例えば、コマンドライン上で

sed -e "s/a=7/a=9/" ./input.ini

と入力すると”input.ini”の中身の”a=7″に一致する場所を”a=9″に置換して出力します。
ここで重要なのが、”a=7″に一致する場所だけなので、後ろにあるコンマは影響されません。
実際に実行してみると

$ sed -e "s/a=7/a=9/" ./input.ini
&input
a=9,
b=13,
c='./dat/',
&end

となってコマンドライン上に出力されます。
この時、書き換わった内容はコマンドラインのみに出力されるため、元のファイル自体に書き換えはされません。

元のファイルの書き換えを行いたければ、出力先を適当なファイル、例えば”tmp”というファイルにし、それを”input.ini”にリネームすればいいです。
すなわち、

sed -e "s/a=7/a=9/" ./input.ini > tmp
mv tmp input.ini

とすればいいのです。実際に実行して中身を見ますと

$ sed -e "s/a=7/a=9/" ./input.ini > tmp
$ mv tmp input.ini
$ cat input.ini
&input
a=9,
b=13,
c='./dat/',
&end

となります。

sedコマンドの概要はここで終了です。
以降は具体例とシェルスクリプトのコード(ファイル名”q.sh”),実行例を載せていきます。

特定の数値を変えたい場合

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
sed -e "s/a=7/a=9/" ./input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=9,
b=13,
c='./dat/',
&end

特殊文字(/等)を含む文字列の変更

sedコマンドを使うために/を使います。ならば/を置換したい場合どうすればいいでしょう。
この時はsedコマンドで使っている区切りを表す/を別の特殊文字(例えば%)に置き換えればよいです。

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
sed -e "s%c='./dat/'%c='./data/'%" input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=7,
b=13,
c='./data/',
&end

置換する数値の変数での指定

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
pr=5
sed -e "s/a=7/a=${pr}/" ./input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=5,
b=13,
c='./dat/',
&ends

ある数値以降を全て変更したい

コンマも含めて消したいとします。
対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
sed -e "s/c=.*/c=12345/" ./input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=7,
b=13,
c=12345
&end

ファイルの空白行の削除

ファイルに含まれる空白行を全て削除します。
対象とするファイル”input.ini”

&input
a=7,

b=13,

c='./dat/',

&end

“q.sh”の中身

#!/bin/sh
sed -e '/^ *$/d' input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=7,
b=13,
c='./dat/',
&end

ファイルの行頭に数値を入れる

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
i=1
while [ ${i} -le 1000 ]
do
sed -e "${i}s/^/${i} /" input.ini > temp
mv temp input.ini

i=`expr $i + 1`
done

実行例

$ sh q.sh
$ cat input.ini
1 &input
2 a=7,
3 b=13,
4 c='./dat/',
5 &end
6

“q.sh”中、1000をファイルに応じて変更してください。

※また、行番号を入れるだけの場合、catコマンドを利用して、

cat -b input.ini > tmp
mv tmp input.ini

とするのが簡単だと思います。
オプション”-b”は空行を含めず行番号を付けるという意味です。空行を含めたい場合は”-n”でできます。

ファイルの最後に改行を入れる

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
sed '$a\\n' input.ini > tmp
mv tmp input.ini

実行例

$ sh q.sh
$ cat input.ini
&input
a=7,
b=13,
c='./dat/',
&end

$

※どうしても2行分改行されてしまうようです。
sedコマンドで1行分の改行は、どうすればよいか分かりませんでした。

苦肉の策ですが、適当なファイル(例えばnn.txt)に改行だけを入力し、catコマンドでファイルを結合すると一応できます。
—nn.txt—

————
を作っておいて、
#!/bin/sh
cat input.ini nn.txt > tmp
mv tmp input.ini
とすれば”input.ini”の後ろに”nn.txt”が結合されるため、1行分の改行が可能です。

do文で何回も変更したい

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
for pr in 0 1 2
do
sed -e "s/a=.*/a=${pr},/" input.ini > tmp
mv tmp input.ini

cat input.ini
done

実行例

$ sh q.sh
&input
a=0,
b=13,
c='./dat/',
&end
&input
a=1,
b=13,
c='./dat/',
&end
&input
a=2,
b=13,
c='./dat/',
&end

全く違う変数を繰り返し代入したい

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
i=1
for j in 3d0 939d0
do
echo "count -> ${i}"
sed -e "s/a=.*/a=${j},/" ./input.ini > tmp
mv tmp input.ini

grep "a=" input.ini

i=`expr $i + 1`
done

実行例

$ sh q.sh
count -> 1
a=3d0,
count -> 2
a=939d0,
$

シェルスクリプトの中の”grep”は”a=”に一致する行を書き出させるものです。

整数の変数を規則的に何回も変更したい

対象とするファイル”input.ini”

&input
a=7,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
i=1
while [ ${i} -le 3 ]
do
echo "count -> ${i}"
sed -e "s/a=.*/a=${i},/" ./input.ini > tmp
mv tmp input.ini

grep "a=" input.ini

i=`expr $i + 1`
done

実行例

$ sh q.sh
count -> 1
a=1,
count -> 2
a=2,
count -> 3
a=3,
$

小数点を含む変数を規則的に何回も変更したい

小数点を含む演算は”expr”コマンドではできません。
シェルスクリプトで数値計算を行う”bc”コマンドを用いましょう。
ここでは、変数$v$に、
$v=i\times0.7,\;\;(i=1,2,3)$
を代入する演算を考えましょう。

対象とするファイル”input.ini”

&input
a=3,
b=13,
c='./dat/',
&end

“q.sh”の中身

#!/bin/sh
i=1
while [ ${i} -le 3 ]
do
echo "count -> ${i}"

v=$(echo "scale=3; $i*0.70 " | bc | sed -e 's/^\./0./g')
echo "$v"

sed -e "s/a=.*/a=${v},/" ./input.ini > tmp
mv tmp input.ini

grep "a=" input.ini

i=`expr $i + 1`
done

実行例

$ sh q.sh
count -> 1
0.70
a=0.70,
count -> 2
1.40
a=1.40,
count -> 3
2.10
a=2.10,
$

あるディレクトリ以下にある全ファイル名を変数にしたい

状況

.
├── a.sh
├── dat
├── data
│   ├── asdfgh.d
│   ├── qwerty.d
│   └── zxcvbn.d
└── input

inputの中身

&input
filename="./data/xxxxx.d",
key = 0,
&end

a.shの中身

#!/bin/sh
i=1
for j in ./data/*
do
sed -e "s%filename=.*%filename="${j}",%" input > tmp
mv tmp ./dat/${j##*/}_ex
echo ${j##*/}
grep "filename=" ./dat/${j##*/}_ex
done

———————-

a.sh実行

$sh a.sh
asdfgh.d
filename="./data/asdfgh.d",
qwerty.d
filename="./data/qwerty.d",
zxcvbn.d
filename="./data/zxcvbn.d",

a.sh実行後の構成

.
├── a.sh
├── dat
│   ├── asdfgh.d_ex
│   ├── qwerty.d_ex
│   └── zxcvbn.d_ex
├── data
│   ├── asdfgh.d
│   ├── qwerty.d
│   └── zxcvbn.d
└── input

例えばdat/asdfgh.d_exの中身

&input
filename="./data/asdfgh.d",
key = 0,
&end

参考先

フィルタを使用した文字列操作 1 -UNIX & Linux コマンド・シェルスクリプトリファレンス
 sed の使い方 -サーバエンジニアの知恵袋
 制御構文 -シェルスクリプト入門
 How to pass results of bc to a variable – Ask Ubuntu
bcによる少数の演算 -SWEng TIPs

物理学

水素原子の解析解1/3 -相対座標と変数分離

2016年2月15日 sikino コメントする

ボーアモデルにおける水素原子の解析解、すなわち電子1個(電荷-e)と陽子1個(電荷+e)の系でスピンを無視する場合を考えます。

戦略1)
この問題をそのまま解こうとすると電子で3次元、陽子で3次元なので、3+3=6次元の問題になります。
私達は今、クーロンポテンシャルが電子–陽子間でしか依存しないことを知っています。
なので、古典力学で知られている通り、相対座標と重心座標を使い分離できそうだ、と考えられます。
やってみましょう。

2体問題における変数分離

2体系を考えます。(参考文献[1])
2つの物体(質量$m_1, m_2$)には2体間の相対距離だけで決まる、時間に依存しないポテンシャル$V({\bf r_1}-{\bf r_2})$で相互作用しています。
よって、この系のハミルトニアン$H$は
$
\displaystyle H=\frac{{\bf p_1}^2}{2m_1}+\frac{{\bf p_2}^2}{2m_2}+V({\bf r_1}-{\bf r_2})
$
となるわけです。それに対応するシュレディンガー方程式は、
$
\displaystyle i\hbar\frac{\partial}{\partial t}\Psi({\bf r_1},{\bf r_2},t)=\left[ -\frac{\hbar^2}{2m_1}\nabla^2_1-\frac{\hbar^2}{2m_2}\nabla^2_2 +V({\bf r_1}-{\bf r_2})\right]\Psi({\bf r_1},{\bf r_2},t)
$
となります。ここで相対座標系
$
\displaystyle {\bf r}={\bf r_1}-{\bf r_2},\;\;\; {\bf R}=\frac{m_1{\bf r_1}+m_2{\bf r_2}}{m_1+m_2}
$
をとります。この座標系ではシュレディンガー方程式は以下のように書き直されます。
$
\displaystyle i\hbar\frac{\partial}{\partial t}\Psi({\bf R},{\bf r},t)=\left[ -\frac{\hbar^2}{2M}\nabla^2_{\bf R}-\frac{\hbar^2}{2\mu}\nabla^2_{\bf r} +V({\bf r})\right]\Psi({\bf R},{\bf r},t)
$
ここで$M=m_1+m_2$は系の全質量、$\mu=\frac{m_1m_2}{m_1+m_2}$は換算質量です。
今、ハミルトニアンが${\bf R}と{\bf r}$のそれぞれの和で書けています。
このことは変数分離が可能であることを示しています。なので波動関数を
$
\Psi({\bf R},{\bf r},t)=\Phi({\bf R})e^{-iE_{CM}t/\hbar}\cdot\psi({\bf r})e^{-iEt/\hbar}
$
として分離し、シュレディンガー方程式に代入、整理すれば$\Phi({\bf R})$と$\psi({\bf r})$に関する方程式
$
\displaystyle -\frac{\hbar^2}{2M}\nabla^2_{\bf R}\Phi({\bf R})=E_{CM}\Phi({\bf R}) \;\;\;\; \ldots(A)
$
$
\displaystyle \left[-\frac{\hbar^2}{2\mu}\nabla^2_{\bf r} +V({\bf r})\right]\psi({\bf r})=E\psi({\bf r})\;\;\;\; \ldots(B)
$
が導けます。
式$(A)$はエネルギー$E_{CM}$の質量$M$の自由粒子に対するシュレディンガー方程式とみなせ、
式$(B)$はポテンシャル$V({\bf r})$中を質量$\mu$を持った粒子に対するシュレディンガー方程式であるとみなせます。
系の全エネルギー$E_{tot}$は
$
E_{tot}=E_{CM}+E
$
です。
適切な座標変換により、2体問題を2つの1体問題に置き換えた。そういう事を今やったのです。

——
水素原子に適応しましょう[2]。
クーロンポテンシャル$V(r)$は
$
\displaystyle V(r)=-\frac{e^2}{4\pi\varepsilon_0 r}
$
と書けます。ここで、$r$は電子–陽子間距離を表します。
電子の質量を$m$, 陽子の質量を$M$と記述します。

重心と共に動く座標系で考えましょう。
今、重心は止まっています(重心の運動量${\bf P}=0$)。
なので、解くべき問題は1体の時間依存しないシュレディンガー方程式だけで、
$
\displaystyle \left[-\frac{\hbar^2}{2\mu}\nabla^2 -\frac{e^2}{4\pi\varepsilon_0 r}\right]\psi({\bf r})=E\psi({\bf r}) \;\;\;\;\; \ldots(1)
$
を解けばよい、ということになりました。$\mu=\frac{mM}{m+M}$はこの系の換算質量を表します。

戦略2)
6次元の問題から重心の自由度を3つ減らして3次元の問題に落とせたわけですが、3次元の問題を解くのはまだまだ大変です。相互作用ポテンシャルが中心力ポテンシャルであることから、3次元極座標で考えればrに関する項は変数分離できて、少なくともrに関する次元が更に1つ落とせそうです。あわよくば、残りの2次元も変数分離出来たら1次元の問題が3つになって嬉しいのですが、果たしてそううまくいくのでしょうか･･･

3次元極座標を用いた変数分離

ここでは3次元極座標、特に球面座標を使って変数分離を試みましょう(実は球面座標以外でも放物座標系と呼ばれる座標を使っても変数分離できます)。

球面座標は、空間を$r,\theta,\phi$を用いて指定する座標です。デカルト座標との間には、

$
\begin{eqnarray}
\left\{
\begin{aligned}
r &=\sqrt{x^2+y^2+z^2} \\
\theta&= \arccos{\frac{z}{r}}\\
\phi&=\tan^{-1}\frac{y}{x}
\end{aligned}
\right.
\;\;\;\;\;\;\;\;
\left\{
\begin{aligned}
x &= r\sin{\theta}\cos{\phi} \\
y &= r\sin{\theta}\sin{\phi} \\
z &= r\cos{\theta}
\end{aligned}
\right.
\end{eqnarray}
$

の関係があり、体積要素$d{\bf V}$は
$
d{\bf V}=r^2\sin{\theta}dr d\theta d\phi
$
と表されます。

波動関数$\psi({\bf r})$を動径方向について分離します。
$
\psi({\bf r})=R(r)Y(\theta,\phi)
$
この座標系でのラプラシアン$\nabla^2$は
$
\displaystyle \nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+\frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial \theta}\left(\sin{\theta}\frac{\partial}{\partial \theta}\right)+\frac{1}{r^2\sin^2{\theta}}\frac{\partial^2}{\partial \phi^2}
$
であるので、これらを式(1)に代入すると、
$
\begin{align}
\displaystyle \left[-\frac{\hbar^2}{2\mu}\left\{\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+\frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial \theta}\left(\sin{\theta}\frac{\partial}{\partial \theta}\right)+\frac{1}{r^2\sin^2{\theta}}\frac{\partial^2}{\partial \phi^2}\right\} -\frac{e^2}{4\pi\varepsilon_0 r}\right]R(r)Y(\theta,\phi)\\
=ER(r)Y(\theta,\phi)
\end{align}
$
を得ます。

調べた限りではここからの解法は2つに分かれます。
①数学的に直接解く
②物理的意味を持つ角運動量演算子を考えながら解く
です。
どちらでも最後は同じになるので構わないと思います。
もしも深く知りたい場合は①を解いてから②を解くことをお勧めします。
長くなるのでページを移します。

①直接解く場合は後ほど

②物理的意味を踏まえながら解く場合は後ほど

参考文献

[1]Physics of Atoms and Molecules 2nd Edition pp.109~111 by B.H. Bransden C.J. Joachain(2003)
[2]Physics of Atoms and Molecules 2nd Edition pp.147~148 by B.H. Bransden C.J. Joachain(2003)
※参考した本はこれです。

Physics of Atoms and Molecules

プログラミングと数値計算

openMPによる並列計算

2016年2月15日 sikino コメントする

まとめ

fortran90では、

program main
implicit none
integer::i,omp_get_thread_num

! number of threads for parallel computation
call omp_set_num_threads(2)

!$omp parallel do
do i=1,100
write(6,*) omp_get_thread_num()
enddo
!$omp end parallel do

stop
end program main

とすれば2個のスレッドで並列計算され、コンパイル時に
intel® fortranでは、

ifort -openmp main.f90

gfortranでは、

gfortran -fopenmp main.f90

とすれば良いです。

fortran90でのお話です。

openMPは複数のCPUを使って並列計算をするインターフェースのことです
C/C++,fortranで対応しています。
何も指定しない場合、計算は基本的に1つのコアのみを使います。
Linuxを使っている場合、恐らくデフォルトで使えるようになっているはずです。

並列計算を行うまでの大まかな手順は2つ。

プログラム内部に文章を書く
コンパイル時にオプションを追加
- intel®fortranコンパイラの場合
- gfortranコンパイラの場合

です。

※今使っているパソコンの並列計算できるCPUの数の確認は、

cat /proc/cpuinfo | grep processor

です。proc/cpuinfoの場所は使っているOSによって違う可能性があります。
”linux mint cpu 確認”
等とgoogle等で検索するのが手っ取り早いでしょう。

プログラム内部に文章を書く

プログラム内でopenMPを使用するdoループを挟むように、

!$omp parallel do
do i=1,100
call test(i)
enddo
!$omp end parallel do

と書きます。基本はこれだけです。
並列計算に使えるスレッドが2個である場合、並列計算というのは

スレッド0

do i=1,50
call test(i)
enddo

スレッド1

do i=51,100
call test(i)
enddo

と割り振る操作なのです。

上記のようにdoループを分割するため、注意しなければならない点として、
doループに用いる変数に対して別々に計算しても計算結果が変わらない事
が挙げられます。
上記例では、i=0から始めて、i=1,2,3,･･･と順次計算する必要は無く、i=5,10,1,3,･･･みたいな乱雑な順番でも計算結果が変わらない状況で使わなければなりません。
特に、i=2を計算したい時にi=1の計算結果を使う場合は並列化することは出来ません。

実際には同期したりとかで、出来なくはないですが面倒くさく、僕はやったことが無いので書きません。

もしも並列計算したいスレッド数を制限したい場合、

!$omp parallel do

を

!$omp parallel do num_threads(2)

のように指定するか(この例ではその部分の並列計算を2つのスレッドで行う)、
並列計算が始まる前のプログラムの初めの方に

call omp_set_num_threads(2)

と書きましょう。これを書くと全ての並列計算箇所が2個のスレッドで行われることになります。

また、関数omp_get_thread_num()はスレッドにつけられた番号を返す事が出来ます。引数は要りません。
なので、これを利用すると何個のスレッドが使われているのか直に確認できます。

補足ですが、MKL(マス・カーネル・ライブラリ)のルーチン内で使われる並列計算のスレッド数は

call mkl_set_num_threads(2)

と書くことで制御できます。

コンパイル時のオプション

intel® fortranでは、

ifort -openmp main.f90

gfortranでは、

gfortran -fopenmp main.f90

としてコンパイル、実行しましょう。

実例

例として

program main
implicit none
integer::i,omp_get_thread_num

! number of threads for parallel computation
call omp_set_num_threads(2)

!$omp parallel do
do i=1,4
write(6,*) omp_get_thread_num()
enddo
!$omp end parallel do

stop
end program main

を動かすと同出力されるか見てみましょう。
gfortranコンパイラで、使えるスレッドの数は2つです。
上記のコードを

gfortran -fopenmp main.f90

としてコンパイルし、実行すると

./a.out
1
0
0
1

という結果が得られます。
ここに出ている数字はスレッドの番号で、0,1と番号付けされたスレッドが確かに出力されている事が分かります。1,0,0,1の順番はどうでも良いです。実行するごとに変わるので、これは同時並行処理されているためでしょう。

call omp_set_num_threads(1)

として計算を行うと、

./a.out
0
0
0
0

と表示されることから、確かに使うスレッド数が制御されていることが分かります。

doループの並列処理を処理が終わった順に行う場合

doループ内で、あるときだけ計算が重くなる場合があります。
この場合、均等にdoループの変数を分けてしまうとCPU1つあたりの処理が大きく異なってしまいます。そこで、doループの変数を終わった順に処理していく指定方法があります。それがschedule構文です。以下のようにすると、i=1から計算が終わった順にiを増やしていきます。

program main
implicit none
integer::i,omp_get_thread_num,N

! number of threads for parallel computation
call omp_set_num_threads(2)

N=100
!$omp parallel do schedule(dynamic,1)
do i=1,N
write(6,*) omp_get_thread_num()
enddo
!$omp end parallel do

stop
end program main

とします。ただし、1回あたり計算時間がほとんどかからない場合、オーバーヘッド時間が無視できなくなるため、使うときは吟味してから使用するべきです。

また、並列化しても共通の変数を使うことができます。以下のようにすると、計算の進み具合がわかります。

program main
implicit none
integer::i,omp_get_thread_num,N,prog

! number of threads for parallel computation
call omp_set_num_threads(2)

N=100
prog=0
!$omp parallel do shared(prog) schedule(dynamic,1)
do i=1,N
write(6,*) omp_get_thread_num()
prog=prog+1
if(mod(prog,50).eq.0)write(6,'(A,i6,A,i6)')" ",prog," / ",N
enddo
!$omp end parallel do

stop
end program main

とします。

経験的に、openmpを使用する際はただ一つのサブルーチンを用いて、並列個所を簡単にするのが良いです。

!$omp parallel do
do i=1,N
a(i)=0
do j=i,N
a(i)=a(i)+1
enddo
a(i)=a(i)*i
enddo
!$omp end parallel do

と、!$~!$につらつらと書くのではなく、

!$omp parallel do
do i=1,N
call test(i,N,a(i))
enddo
!$omp end parallel do

として、サブルーチン１つにするだけの方がバグが出にくいです。

openMPの機能はこれだけではありません。
調べることをお勧めします。ここではこれ以上書きません。

参考文献

インテル® コンパイラーOpenMP*入門

gnuplot, 数学

正多角形とスピログラフの数式

2016年2月14日 sikino 6件のコメント

正多角形とスピログラフの数式です。

正多角形(2次元)
正多角形(3次元)
星型多角形(2次元)
星型多角形(3次元)
トロコイド(2次元)
トロコイド(3次元)
スピログラフ

2016/10/24
幾何学模様を作りたい方は幾何学模様(gnuplot)へどうぞ。

[adsense1]

正多角形の式(2次元)

正n角形の数式は[1]を参考に修正しました。
正n角形の数式は、
$
\begin{equation}
\left\{
\begin{aligned}
x&\displaystyle =\cos t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}\\
y&\displaystyle =\sin t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}
\end{aligned}
\right.
\end{equation}
$
です。ここで、$a_n=\frac{2\pi}{n}$と置きました。また、${\rm floor}(x)$は床関数(床関数と天井関数)を表します。
媒介変数$t$の範囲は($0\le t \lt 2\pi$)です。
グラフを書かせてみますとこうなります。

n=3,4,5,6
n=7,8,9,10の順で、単位円を一緒に記述しています。
線の色の濃さは媒介変数の値に応じて変化させています。

gnuplotのスクリプトはこちら

▼クリックでこの場に展開

多面体の式(3次元)

半径1の多面体は、平面のx,yの媒介変数による正n角形の関数をそれぞれpc(t),ps(t)と置くと、
$
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm ps}(u)\cdot {\rm pc}(v) \\
y& = {\rm ps}(u)\cdot {\rm ps}(v) \\
z& = {\rm pc}(u)
\end{aligned}
\right.
\end{equation}
$
と書けます。
媒介変数$u,v$の範囲は($0\le u \lt \pi, \;\; 0\le v \lt 2\pi$)です。

プロットすると以下のようになります。

n=3,4,5,6
n=7,8,9,10の順です。

gnuplotスクリプトはこちら

▼クリックでこの場に展開

星型多角形(2次元)

$
\begin{equation}
\left\{
\begin{aligned}
x&\displaystyle =\cos t \cdot \frac{\cos a_n}{\cos\left[a_n -\frac{1}{n}\cos^{-1}\{\cos(nt)\}\right]}\\
y&\displaystyle =\sin t \cdot \frac{\cos a_n}{\cos\left[a_n -\frac{1}{n}\cos^{-1}\{\cos(nt)\}\right]}
\end{aligned}
\right.
\end{equation}
$
です($n\ge 5$)。ここで、$a_n=\frac{2\pi}{n}$と置きました。
グラフを書かせてみるとこのようになります。

gnuplotスクリプトはこちら。
※$\cos^{-1}(\cos(x))$は不安定です。
場合により書けなくなることがあります。ここでは上記関数の代わりに、正弦波ではない周期関数の数式
で記述した関数$s(a,x)$を用いています。

▼クリックでこの場に展開

星型多角形(3次元)

3次元の場合は多面体の時と同じように、平面のx,yの媒介変数による星型多角形の関数をそれぞれstpc(t),stps(t)と置くと、
$
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm stps}(u)\cdot {\rm stpc}(v) \\
y& = {\rm stps}(u)\cdot {\rm stps}(v) \\
z& = {\rm stpc}(u)
\end{aligned}
\right.
\end{equation}
$
と書けます。
媒介変数$u,v$の範囲は($0\le u \lt \pi, \;\; 0\le v \lt 2\pi$)です。
グラフはこのようになります。

gnuplotスクリプトはこちら。

▼クリックでこの場に展開

トロコイド(2次元)

トロコイドと呼ばれる曲線があります[2]。
これをgnuplotで書いてみましょう。数式は[2]を参考にして以下の通りです。
$
\begin{equation}
\left\{
\begin{aligned}
x& = \left[(n-1)\cos t +h\cos((n-1)t)\right]/n \\
y& = \left[(n-1)\sin t +h\sin((n-1)t)\right]/n
\end{aligned}
\right.
\end{equation}
$
$h=1$の時、半径が1の円に内接するように決めています。
また、$n$が整数の時、内接する円が外側の円をちょうど一周回った時に元の位置に戻る条件です。
別に整数でなくても構いません。その時はもっと複雑なものになることでしょう。

書いてみますと曲線はこうなります。
自由度$h$を1にしてグラフを書いてみましょう。

自由度hを少し変えてみましょう。

▼クリックでこの場に展開

トロコイド(3次元)

3次元の場合は多面体の時と同じように、平面のx,yの媒介変数によるトロコイドの関数をそれぞれhcyc(t),hcys(t)と置くと、
$
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm hcys}(u)\cdot {\rm hcyc}(v) \\
y& = {\rm hcys}(u)\cdot {\rm hcys}(v) \\
z& = {\rm hcyc}(u)
\end{aligned}
\right.
\end{equation}
$
と書けます。
媒介変数$u,v$の範囲は($0\le u \lt \pi, \;\; 0\le v \lt 2\pi$)です。

n=3,4,5,6
n=7,8,9,10の順です。

gnuplotスクリプトはこちら

▼クリックでこの場に展開

[adsense2]

スピログラフ(2次元)

図示すれば、スピログラフと言うのは

という二つの円からなる軌道です。黄色の点線の長さが等しい、という束縛条件が課せられます。
数式は上のトロコイドと同じで
$
\begin{equation}
\left\{
\begin{aligned}
x& = \left[(n-1)\cos t +h\cos((n-1)t)\right]/n \\
y& = \left[(n-1)\sin t +h\sin((n-1)t)\right]/n
\end{aligned}
\right.
\end{equation}
$
と書けます。

もう少し考えを一般化して、周りを取り囲んでいる形状が円ではない時を考えましょう。その時の数式を考えます。
考え方はトロコイドと一緒ですが、もう少し拡張しましょう。

今、2つの媒介変数による軌道を持っていたとします。１つの媒介変数の軌道上を動かせばスピログラフの考えと同じになります。図で示すと以下のようになります。

スピログラフは両方円であり、滑りが無い(cを決定する条件)場合に対応するわけです。ただ、円である必要性はないので、多角形であろうが、何だろうが数式上では書けるわけです。
興味深い事に、大きな軌道に沿って小さな軌道を動かした、と見ようが小さな軌道に沿って大きな軌道を動かしたとみても数式上では一緒なのです。面白いですね。

いくつか例を挙げます。
五角形上を動かす場合はこうです。

数式として,
$
\begin{equation}
\left\{
\begin{aligned}
x& = f_{1x}(t)+r\cdot f_{2x}(s\cdot t) \\
y& = f_{1y}(t)+r\cdot f_{2y}(s\cdot t)
\end{aligned}
\right.
\end{equation}
$
と書き表すことにします。これを元にgnuplotのスクリプトを書けば以下のようになります。

▼クリックでこの場に展開

色々に変化させた時の色々なときのグラフです。

rを綺麗な数字にしなければもっと複雑な図が得られます。
また、この考え方は3つの媒介変数の軌道、4つの媒介変数の軌道…として容易に拡張できます。
もっと複雑な模様が欲しければ、もう少し増やしてみましょう。

例えば3つの場合はこうなります。

このスクリプトを置いておきます。

▼ここクリックでgnuplotスクリプト展開

この考えを拡張していくと”フーリエ級数の図示化”と言うのができるわけです。

実際にやっている方がいるので紹介しておきますね。

k_1(x)=のところに好きな関数（数列）を入れて遊べるフーリエ級数視覚化マシーンを作りましたhttps://t.co/GmQo5NoZbz pic.twitter.com/vHrQ32FdWw

— 鯵坂もっちょ (@motcho_tw) 2016, 2月 6

参考文献

[1]Is there an equation to describe regular polygons? -MATHEMATICS
[2]Hypotrochoid -Wolfram Mathworld

[3]Is there an equation to describe regular polygons? -Mathematics
2021/11/29追記）滑らかに星と円を遷移する場合、このページが丁寧です。

gnuplot, 数学

アニメーションに便利な関数

2016年2月11日 sikino コメントする

アニメーションに便利な関数、手法です。

点の表示

plot sprintf("< echo ''%f %f''", x0,y0)

とすると点$(x_0,y_0)$が描写されます。

窓関数

窓関数です。関数$W(x)$は、
$
\displaystyle W(x)=\frac{r^{2^n}}{(x-x_c)^{2^n}+r^{2^n}}
$
書かれます。この関数は$r$が窓の横幅を示し、$n$が窓の端の様子を決めるパラメータです。窓の広がりはおよそ$2r$です。

fwi(n,r,i,ic)=(real(r)**(2**n))/((real(i-ic))**(2**n)+real(r)**(2**n))

加速、減速

$
\begin{align}
y(x)&=C_0\tanh(a(x-x_c))+C_1 \\
& C_0 = \frac{f_0-f_1}{t_0-t_1} \\
& C_1 = \frac{-t_1f_0+t_0f_1}{t_0-t_1} \\
& t_0 = \tanh(a(x_0-x_c)) \\
& t_1 = \tanh(a(x_1-x_c)) \\
& x_c = \frac{x_0+x_1}{2}
\end{align}
$
の関数は点$(x_0,y_0)$から点$(x_1,y_1)$に$\tanh(ax)$で与えられる関数で書きます。
関数の中心は$(x_c,y_c)=((x_0+x_1)/2,(y_0+y_1)/2)$になります。
画像の2つの赤い点は$(x_0,y_0)$と$(x_1,y_1)$を表しています。
$a$は変化の度合いを調節するパラメータです。

この関数は非常に使えます。ラミエルを作っている最中にこの関数を考えましたが、想像以上に役立ちます。

fth(a,x,x0,f0,x1,f1)=(f0-f1)*tanh(a*(real(x)-(x0+x1)*0.5e0))/(tanh(a*(real(x0)-(x0+x1)*0.5e0))-tanh(a*(real(x1)-(x0+x1)*0.5e0)))+(-f0*tanh(a*(real(x1)-(x0+x1)*0.5e0))+f1*tanh(a*(real(x0)-(x0+x1)*0.5e0)))/(tanh(a*(real(x0)-(x0+x1)*0.5e0))-tanh(a*(real(x1)-(x0+x1)*0.5e0)))
# x0,f0 --> x1,f1

この関数を用いた応用です。

これはある時間内で高さを反転させるものです。コードはこちら。

set xr[-6:6]
set yr[0.8:2.2]
set size ratio 0.5 1

a=1e0
at=0.4e0
x0=-5e0
f0=1e0
x1=5e0
f1=2e0

#set term gif enhanced animate optimize delay 8 size 800,500
#set output 'extime_tanh.gif'

i0=0
i1=20
do for[i=i0:i1]{
ft0=fth(at,i,i0,f0,i1,f1)
ft1=fth(at,i,i0,f1,i1,f0)
plot fth(a,x,x0,ft0,x1,ft1) w l lt 2 lc 3 lw 5 ti sprintf("a=%3.2f, at=%3.2f, (x_0,f_0)=(%3.2f,%3.2f), (x_1,f_1)=(%3.2f,%3.2f)",a,at,x0,f0,x1,f1), sprintf("< echo ''%f %f''", x0,ft0) pt 7 ps 2 lc 7, sprintf("< echo ''%f %f''", x1,ft1) pt 7 ps 2 lc 7

}

#set out
#set terminal wxt enhanced

数学

Wolfram alphaの便利な使い方

2016年2月3日 sikino コメントする

オンラインで使える数学用の検索エンジン
Wolfram alpha
を使うといろいろな事が出来ます。それらを紹介します。

積分

integral from 0 to infty sin(x)/x

基本中の基本、積分です。複雑な積分でも定積分でも不定積分でも無限大でも受け付けてくれます。
ただし、計算してくれるかは分かりません。
例えば$\rm{sinc}$関数$\left(\rm{sinc}(x)=\frac{sin(x)}{x}\right)$のゼロから無限大までの積分は、

のように出力してくれます。$\pi$で出力されるのは凄いです。

$\rm{sinc}$関数のように有名な関数であれば、

integral sin(x)/x

としたほうがたくさんの情報が得られます。

微分方程式の解

y''(x)+y(x) = sin(x)

と入力すると微分方程式を解いてくれます。また、

y''(x)+y(x) = sin(x), y(0)=1, y'(0)=0

な風にすると、初期条件を与えたうえで解いてくれます。

自分の与えた数式通りに認識しているか、確かめましょう。

行列の対角化

Eigenvectors[{-2,2,4},{-2,4,2},{-2,1,4}]

行列の対角化を行ってくれます。上を入力すると行列
$
\begin{eqnarray}
\left(
\begin{array}{ccc}
-2 & 2 & 4 \\
-2 & 4 & 2 \\
-2 & 1 & 4
\end{array}
\right)
\end{eqnarray}
$を対角化し、その固有値と固有ベクトルを出力してくれます。