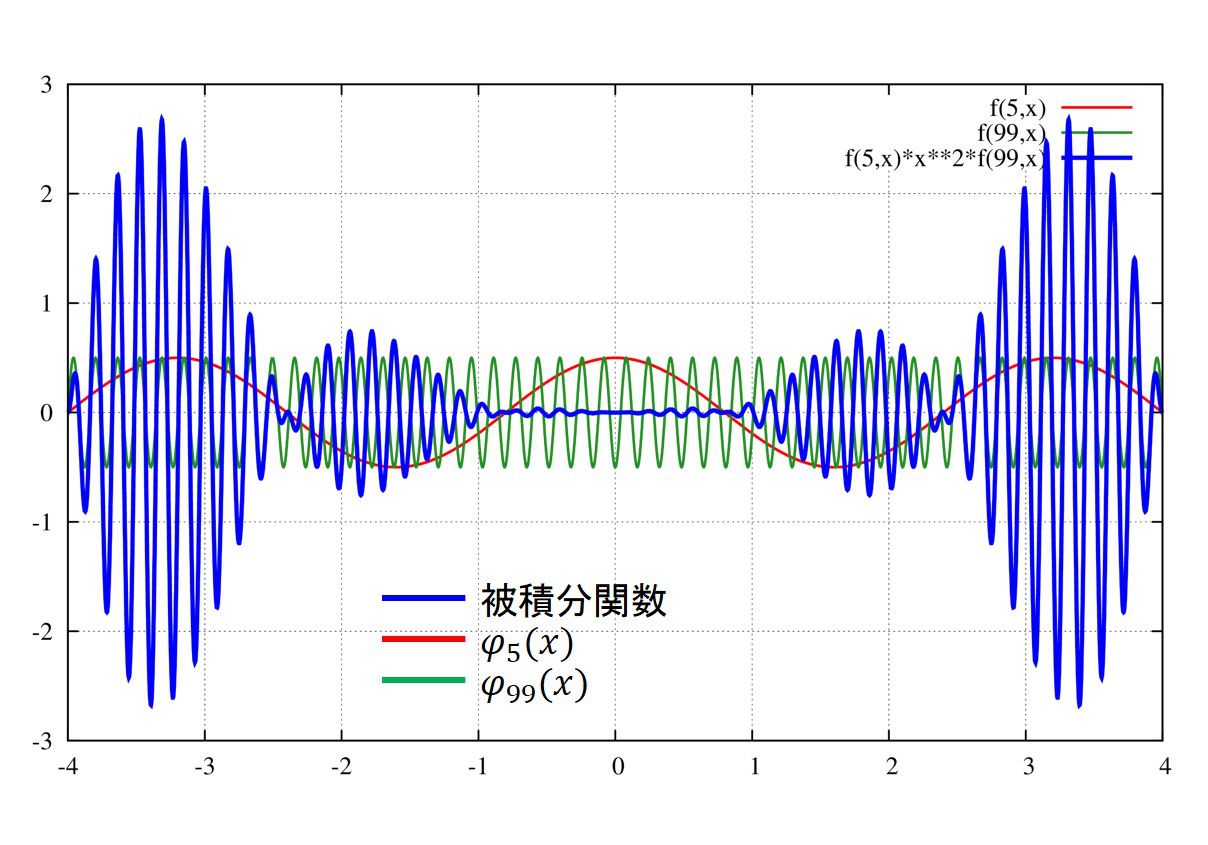
計算例

具体的に適当なポテンシャルの形を考えて解いてみましょう。

プログラムは
時間依存しないシュレーディンガー方程式と変分原理 1/2
にあります。

おさらいですが、間接法による変分原理は、

• 固有値の上限を与える（変分原理によるエネルギー固有値は必ず厳密なエネルギー固有値よりも大きくなる）
• 基底関数の数を増やすほど精度は上がる(完全系の場合)

ということを想定しています。
そして、時間依存しないシュレーディンガー方程式と変分原理 1/2 （計算手法の説明）
では、これから束縛状態のみを考えるので、sin関数系の場合の変分原理について計算を行っていきました。
上に想定した変分原理の想定は、

正しい境界条件の下で誤差なく行列要素が求められ、誤差なく対角化が行われた

場合にのみ成り立ちます。sin関数系の場合の境界条件は固定端条件、つまり区間[a,b]で
\(
\psi(x=a)=\psi(x=b)=0
\)
ということです。

ここでは、解析的な解が存在する

1. 井戸型ポテンシャル
2. 三角量子井戸
3. 調和ポテンシャル
4. F.モースによるポテンシャル[3]
5. \(1/(\cosh^2)\)型ポテンシャル[3]
6. クーロンポテンシャル(動径方向, \(l=0\))

について比較していきます。

シュレーディンガー方程式は全て原子単位系(\(m=1, \hbar=1\))で考え、
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+V(x)\right]\psi(x)=E\psi(x)
\)
の形を考えます。

無限に深い井戸型ポテンシャル

ポテンシャル

\(
V(x)=\left\{
\begin{eqnarray}
0 \hspace{2em}&(& 0\lt x \lt L,)\\
\infty \hspace{2em}&(& x\le 0 \ or\ L\le x)
\end{eqnarray}
\right.
\)
※井戸の区間が\([a,b]\)であっても変数変換\(y=x-a,\;\;L=b-a\)によって上記ポテンシャルの形に変換されます。

固有値

\(
\displaystyle E_n=\frac{(n+1)^2\pi^2}{2 L^2},\;\;(n=0,1,2,\cdots)
\)

固有関数

\(
\psi_n(x)=\left\{
\begin{eqnarray}
\sqrt{\frac{2}{L}}\sin\left(\frac{(n+1)\pi}{L}(x+\frac{L}{2})\right) &(& 0\lt x \lt L,)\\
0 \hspace{6em}&(& x\le 0 \ or\ L\le x)
\end{eqnarray}
\right.
\)

解法

区間\(0\lt x \lt L,\)ではシュレーディンガー方程式の\(V(x)=0\)の解、sin,cosの形をしてなければなりません。
また、\(\psi(x=0)=0,\;\psi(x=L)=0\)では境界条件より、波動関数の値はゼロです。
よって、解はsin,cosの形で、そのゼロ点がちょうど\(x=0,x=L\)にくるような関数となります。

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[0,\(\pi\)]
基底関数の数(N)：200

エネルギー固有値

考察

行列は元々対角です。なので、対角化する前から対角行列です。
誤差は入りようがありません。

三角量子井戸

ポテンシャル

\(
V(x)=\left\{
\begin{eqnarray}
\infty \hspace{2em}&(& x\lt 0)\\
\alpha x \hspace{2em}&(& 0 \lt x)
\end{eqnarray}
\right.
\)

固有値

\(
\displaystyle E_n=-\left(\frac{\alpha^2}{2}\right)^{1/3}a_n
\)
ここで、\(a_n\)はAiry関数[4]のゼロ点です。

固有関数

\(
\displaystyle \psi_n(x)=C\cdot \text{Ai}\left(\left(\frac{2}{\alpha^2}\right)^{1/3}(\alpha x-E_n)\right)
\)
※積分区間がエアリー関数のゼロ点から無限までであり、これは解析的に実行できません。なので規格化定数をあらわに書くことはできません。

解法

区間\(0\lt x \lt \infty,\)ではシュレーディンガー方程式の\(V(x)=\alpha x\)の解、Airy関数の形をしてなければなりません。
また、\(\psi(x=0)=0, \psi(x\to \infty)=0\)の境界条件を満たします。
よって、解はAiry関数の形で、\(x\)が漸近で減衰していく方の解(\(Ai(x),Bi(x)\)のAiの方)で、そのゼロ点がちょうど\(x=0\)にくるような関数となります。

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[0,60]
基底関数の数(N)：200
\(\alpha\)：1

エネルギー固有値

考察

上記計算では基底状態から励起状態までほとんど精度が変わっていません。
また、変分原理が想定したとおり、全ての数値計算解は、厳密な解よりも高い結果を与えています。
厳密な解よりも高い結果を与えていることから、
行列要素は高精度で計算されているが、基底関数が足らない、もしくは計算区間が足らない
事が考えられます。

精度がなぜ良くないのかを考えましょう。
\(x=0\)の境界条件は\(\sin\)関数で良く表現されます。が、\(x\to\infty\)側は指数関数で減少していきます。
(一次の)指数関数で減衰していくことを\(\sin\)関数系ではうまく表現できないのではないか、と思います。
実際、Airy関数の指数関数での減衰は漸近で
\(
\displaystyle \frac{e^{-\frac{2}{3}x^{3/2}}}{x^{1/4}}
\)
と表されます。
この後、調和ポテンシャルとクーロンポテンシャルの場合も考えますが、
調和ポテンシャル(漸近で\(\exp(-x^2)\)、基底状態の精度14,15桁)
↓
三角量子井戸(漸近でおおよそ\(\exp(-x^{2/3})\)、基底状態の精度7,8桁)
↓
クーロンポテンシャル(漸近で\(\exp(-x)\)、基底状態の精度2,3桁)
の順に精度が悪くなっていきます。
指数関数的な減衰が早い≒無限に深い量子井戸
を意味するはずなので、恐らくこうなのではと思います。

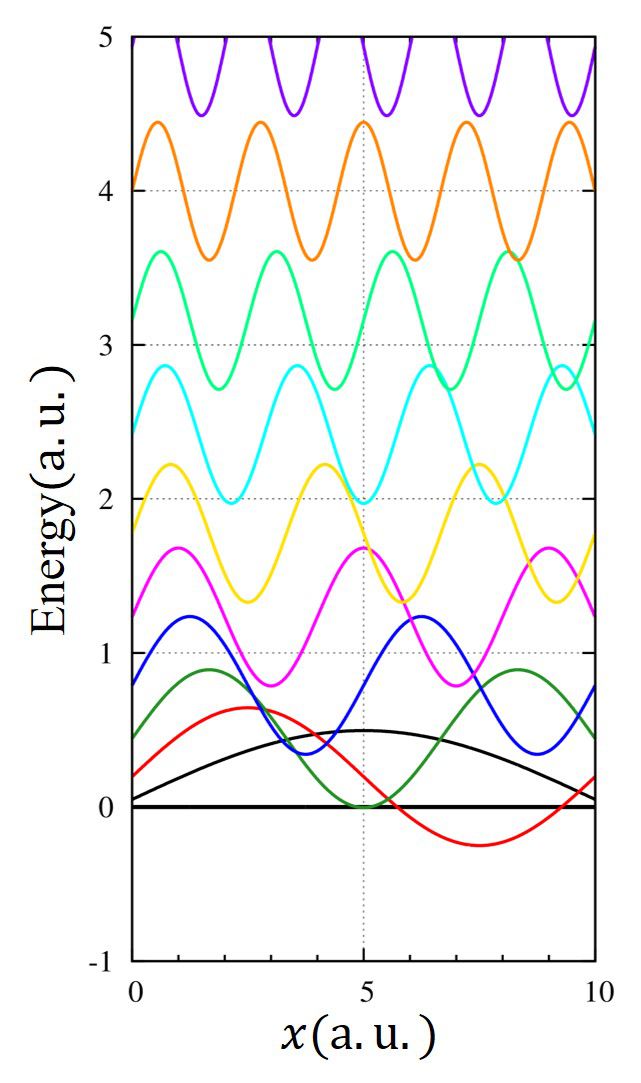
調和ポテンシャル

\(
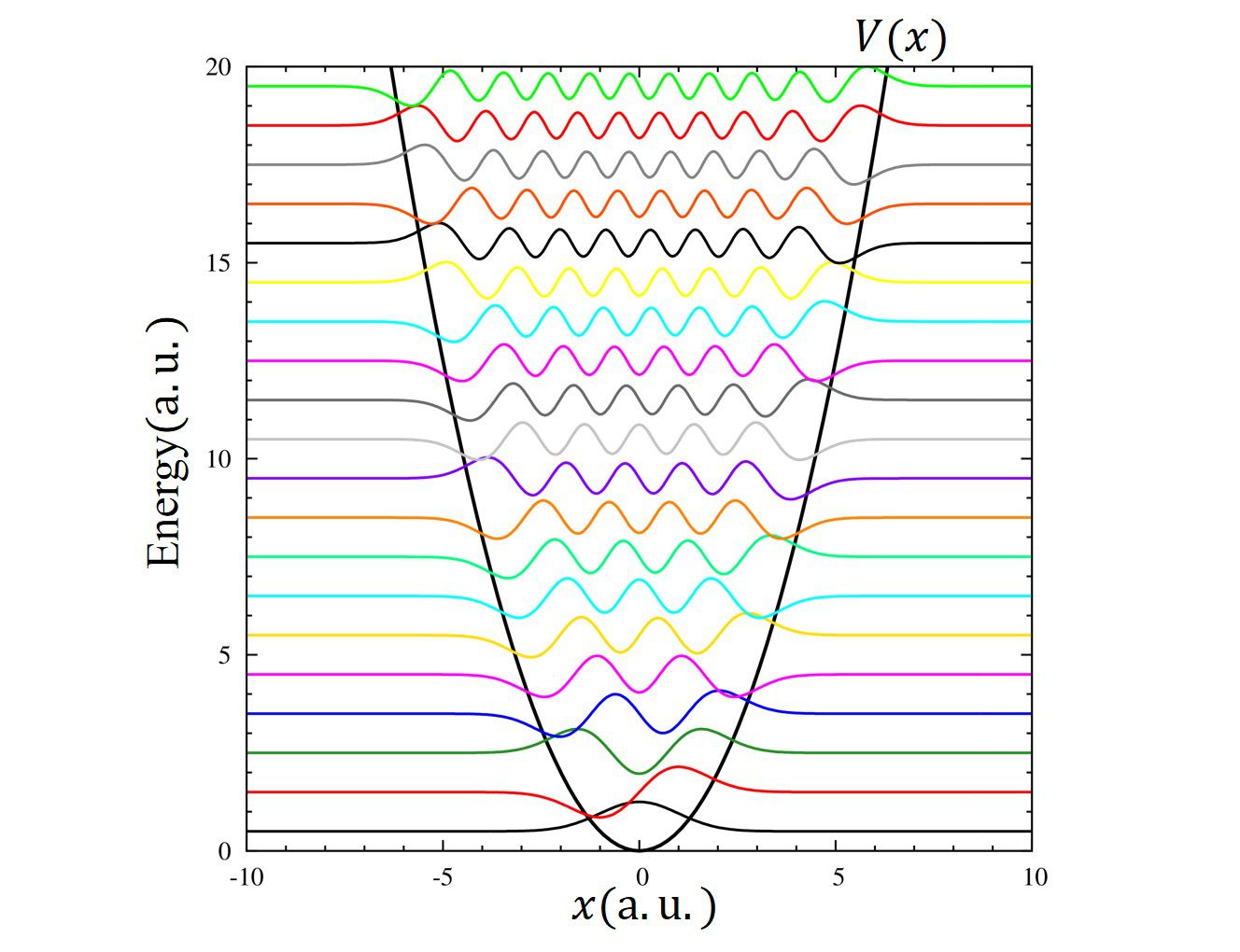
\displaystyle V(x)=\frac{1}{2}x^2
\)

固有値

\(
\displaystyle E_n=n+\frac{1}{2},\;\;(n=0,1,2,\cdots)
\)

固有関数

\(
\displaystyle \psi_n(x)=\frac{\pi^{-1/4}}{\sqrt{2^n n!}}e^{-\frac{x^2}{2}} H_n\left(x\right)
\)
ここで\(H_n(x)\)はエルミート多項式を表します。

解法

1次元調和振動子の直接解法

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[-30,30]
基底関数の数(N)：200

考察

変分原理の典型的な傾向を見せています。というのは高い励起状態になればなるほど精度が悪くなっているためです。
高励起状態になるにつれて精度が悪くなっていくのは基底関数が足らない為でしょう。計算区間に関してはポテンシャルは境界で高いまま(\(V(a)=V(b)=450\))であり、求められたエネルギー固有値の値\(E_{50}\approx 50\)と比べても十分大きいです。なので、計算区間は足りています。

また、変分原理の固有値の上限を与えるに関しては必ずしも満たしているわけでは無いことに気が付きます。これは行列要素を求める際の誤差や丸め誤差に起因するものであると考えられます。なので、原理が破られているのではなく、数値計算上の問題に起因しています。\(n=30,40,50\)では厳密解よりも大きな値を与えています。これは、数値計算上の誤差よりも変分原理の原理的な値の方が大きくなっているためです。

F.モースによるポテンシャル[3]

\(
\displaystyle V(x)=A\left(e^{-2\alpha x}-2e^{-\alpha x}\right)
\)

固有値

\(
\displaystyle E_n=-A\left[1-\frac{\alpha}{\sqrt{2A}}\left(n+\frac{1}{2}\right)\right]^2
\)
ここで、\(n\)は正の整数で、ゼロから始まり、
\(
\displaystyle\frac{\sqrt{2A}}{\alpha}\gt n+\frac{1}{2}
\)
を満足する最大値\(n_{\text{max}}\)まで。

固有関数

\(
\begin{align}
\psi(x)&=e^{-\xi/2} \xi^s w(\xi) \\
& w(\xi)=F(-n,2s+1,\xi) \\
& \xi=\frac{2\sqrt{2A}}{\alpha}e^{-\alpha x} \\
& s=\frac{\sqrt{-2E}}{\alpha}
\end{align}
\)
ここで\(F(a,b,x)\)は合流型超幾何関数です。

この問題では離散スペクトルは有限個だけ存在します。もしも
\(
\displaystyle\frac{\sqrt{2A}}{\alpha}\gt n+\frac{1}{2}
\)
であれば、離散スペクトルは一般に存在しません。

解法

[3]を参照してください

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[-3,80]
基底関数の数(N)：200
\(A\)：5
\(\alpha\)：1

エネルギー固有値

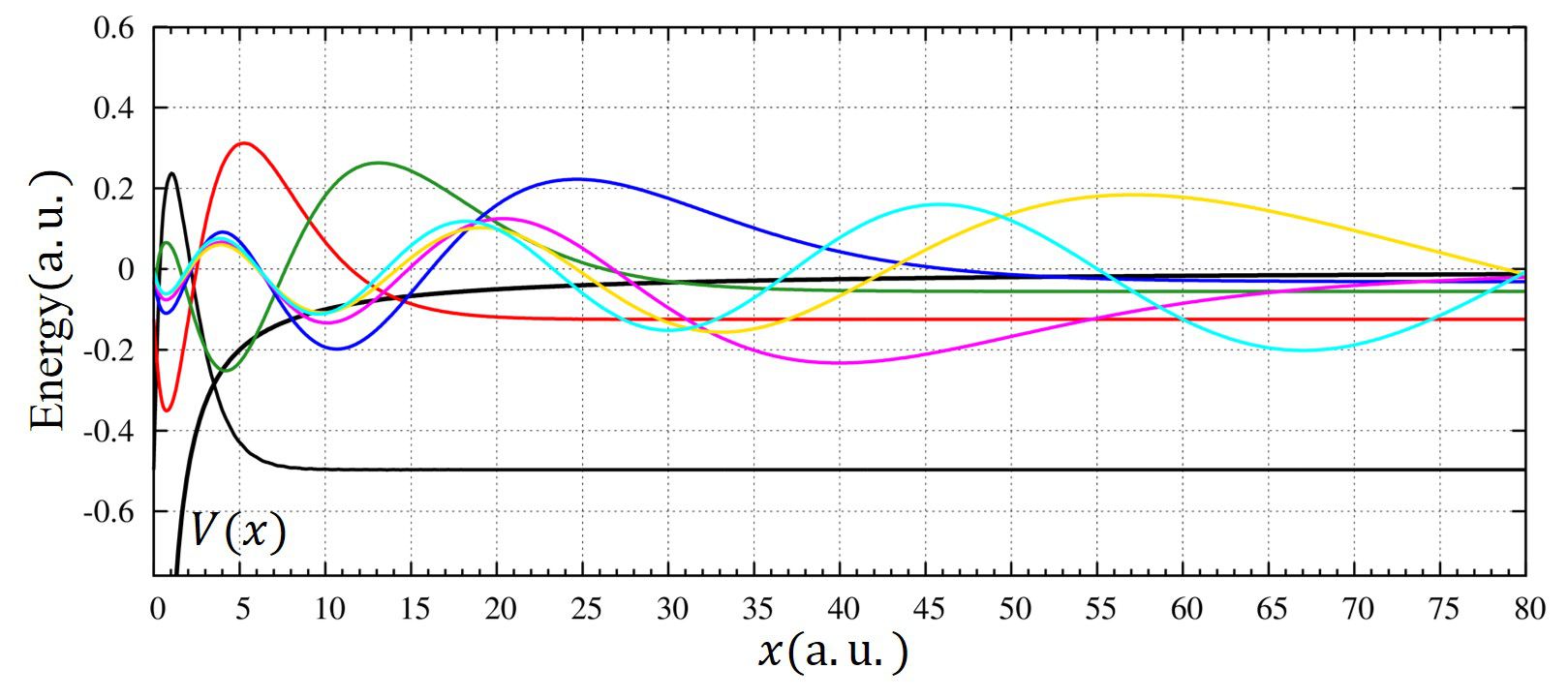
考察

厳密解は3つしか存在しません。この3つの状態に対しては数値計算解の方が厳密解よりも大きくなり、想定通りです。
しかし精度があまり良くありません。これはポテンシャルが\(V(x\to\infty)=0\)であり、波動関数が速やかにゼロに向かわないためだろうと考えられます。
また、基底状態でもあまり良い結果が得られていません。上記ポテンシャルの閉じ込めが強くなく、多くの基底関数が必要となり、数値計算で用いた200個では十分ではないのでしょう。

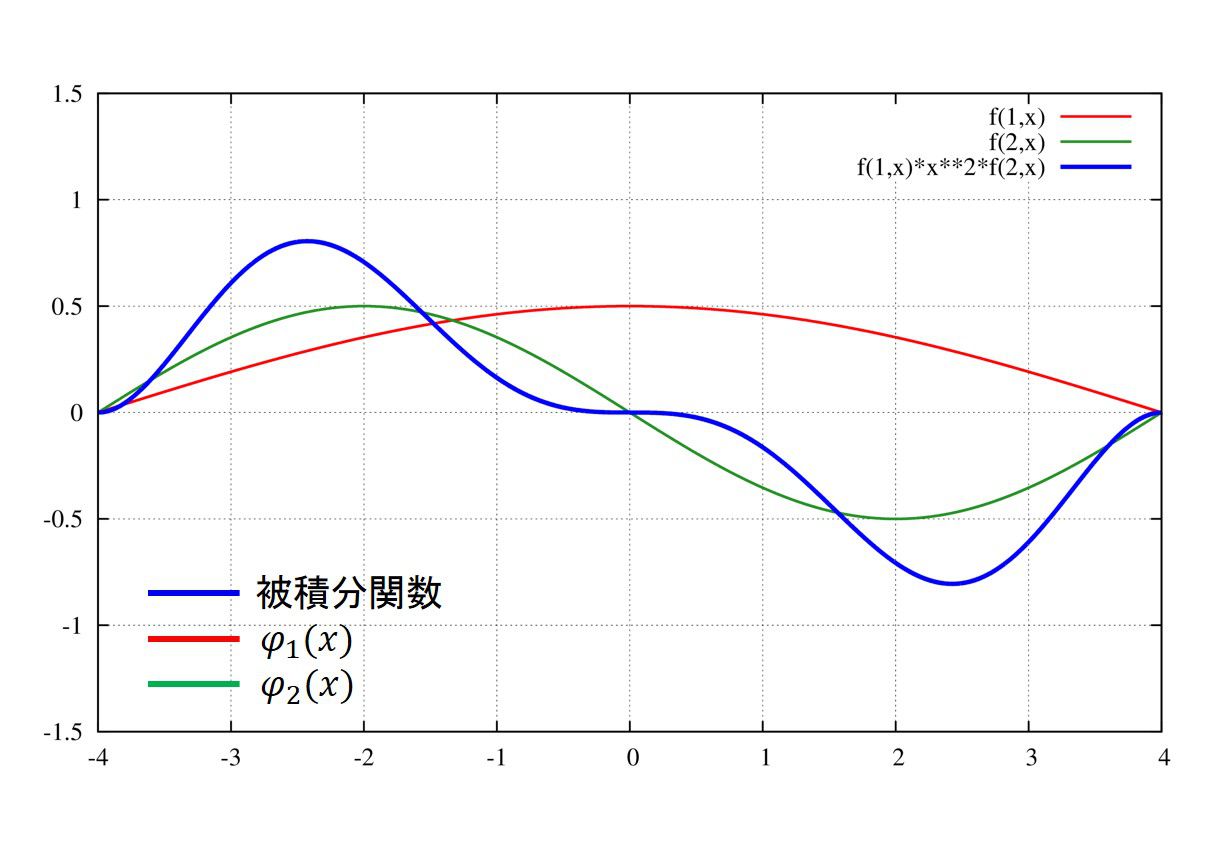
4つ目の解に注目しましょう。厳密解は存在しないのに数値計算ではあたかも解が存在するように見えます(\(E\le 0\))。また、変分原理は上限を与えるため、4つ目の解が存在すると考えてしまうかもしれません。しかし、これは違います。明らかにするために4つ目の解の波動関数の形(青色の線)を拡大してみますと、

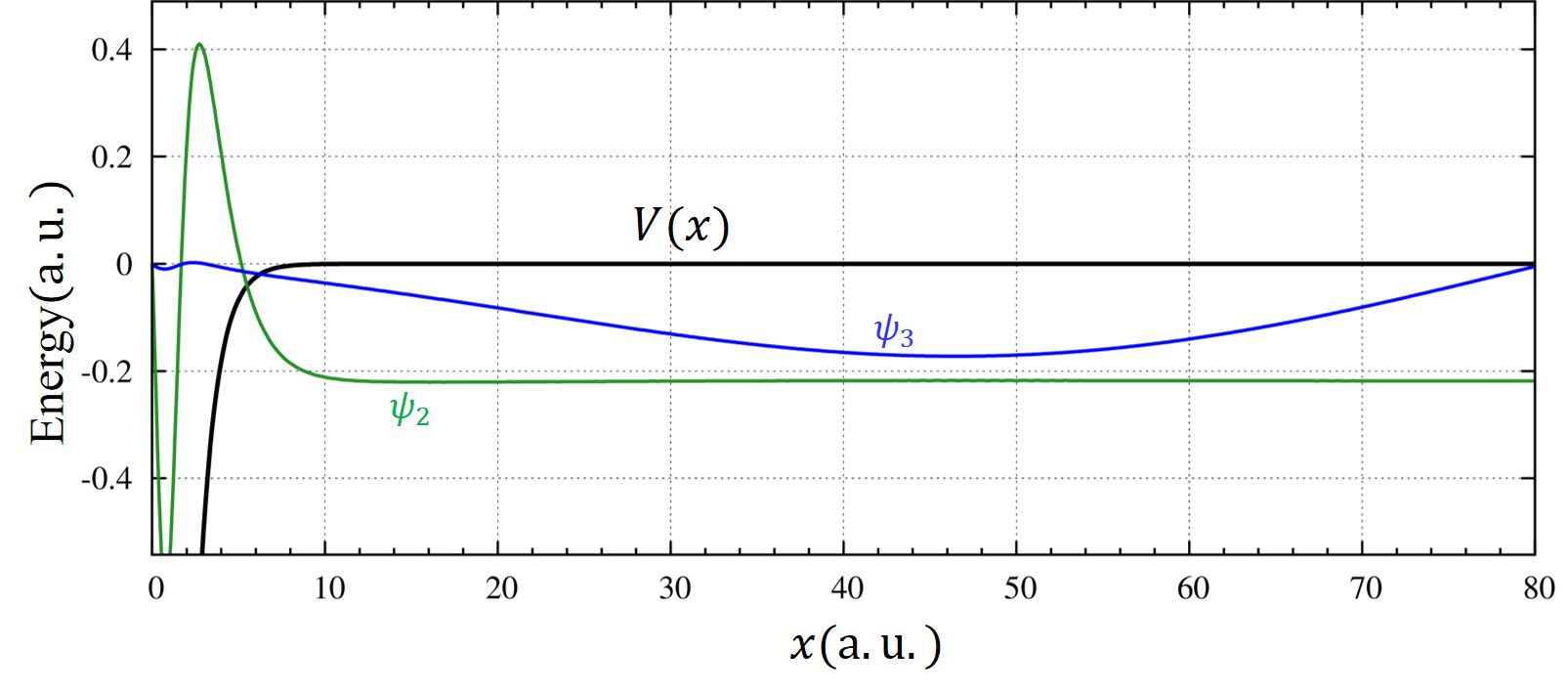
となり、物理的に意味を成していないことが分かります。なぜなら、波動関数は\(x\to\infty\)に向かうにつれて徐々に小さくなっていかなければなりません。もしもこれが正しければ、\(x=80\)で節を持っている解ということになり、これは束縛状態の解としては適しません。

エネルギー固有値だけを考えては求められないものだったということですね。

さらに、束縛状態以上ではすべて連続状態です。それにもかかわらず\(E\gt 0\)でも離散的に固有値が得られているのは基底関数に固定端の境界条件を課しているためです。これらに物理的な意味は無いので評価する際には気を付けましょう。

\(1/(\cosh^2)\)型ポテンシャル[3]

\(
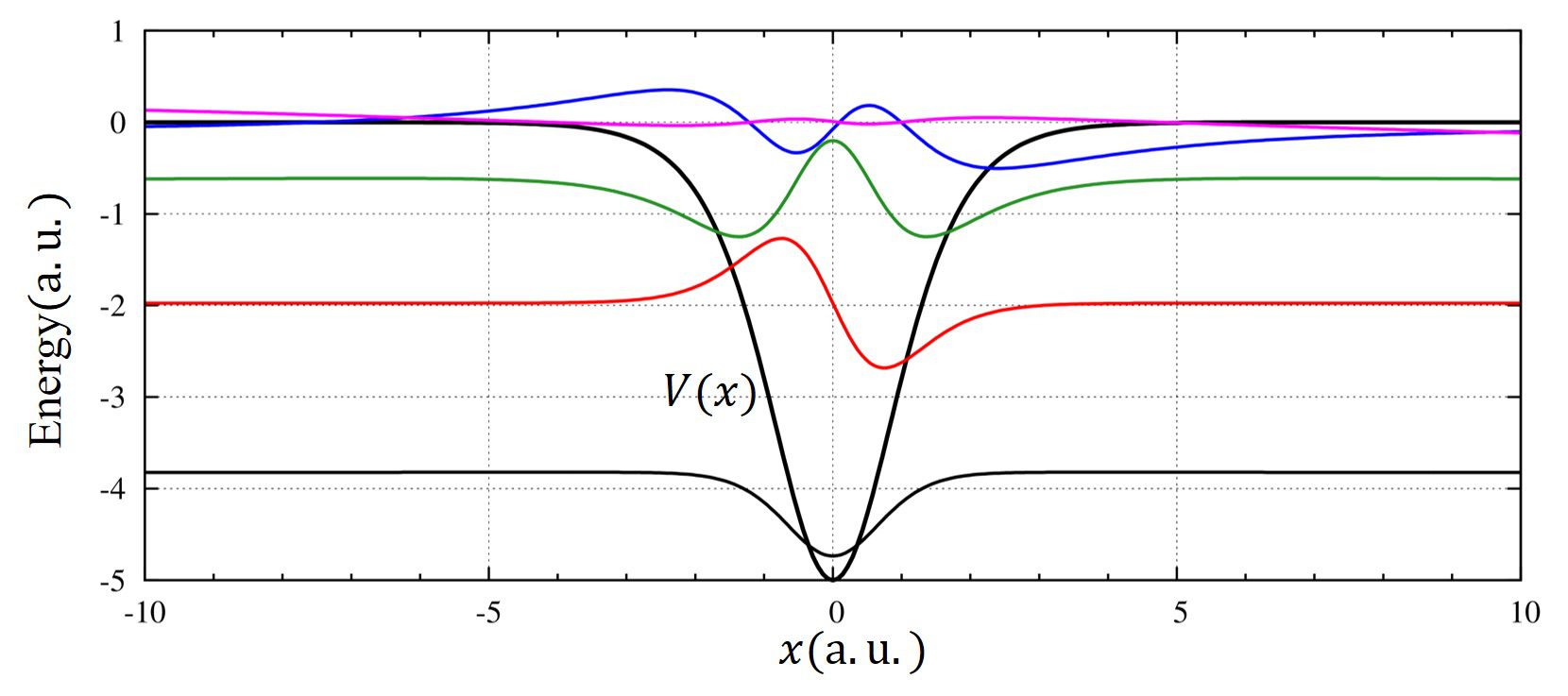
\displaystyle V(x)=-\frac{V_0}{\cosh^2 \alpha x}
\)

固有値

\(
\displaystyle E_n=-\frac{\alpha^2}{8}\left[-(1+2n)+\sqrt{1+\frac{8V_0}{\alpha^2}}\right]^2
\)
で、\(n\)は
\(
\displaystyle n\lt s = \frac{1}{2}\left(-1+\sqrt{1+\frac{8V_0}{\alpha^2}}\right)
\)
から有限個の準位が決まります。

固有関数

\(
\begin{align}
\psi(x)&=(1-\xi^2)^{\xi/2}F\left[\varepsilon-s, \varepsilon+s+1, \varepsilon+1, \frac{1-\xi}{2}\right]\\
& \varepsilon=\frac{\sqrt{-2E}}{\alpha}\\
& \xi=\tanh \alpha x
\end{align}
\)
ここでの\(F(a,b,c,x)\)は超幾何関数です。

解法

[3]を参照してください

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[-30,30]
基底関数の数(N)：200

エネルギー固有値

考察

エネルギー固有値の上限を確かに与えています。そのほかはおおよそF.モースによるポテンシャルと同じような結果を与えています。

精度に関して、エネルギー固有値の精度は\(n=0,2\)の時、1~2桁程度の精度ですが、\(n=1,3\)の時、は6~7桁一致と著しく精度が上がっています。計算区間を変えたりしたのですが、この傾向は変わりません。
なぜなのか…詳しくは分かりません。偶関数、奇関数の問題だと思います。すなわち、奇関数の場合はなにか\(x\gt 0\)の領域に誤差があっても同じ量の誤差で\(x\lt 0\)で打ち消し合ってくれるのですが、偶関数の場合は打ち消し合いが起きないのではないか、ということです。
ただ、これが行列要素の精度からくるものなのかは詳しく見ていないので分かりません…

クーロンポテンシャル(動径方向, \(l=0\))

ポテンシャル

\(
\displaystyle V(x)=-\frac{1}{x}
\)
※ここでは、一階微分の存在しない形にした時のシュレーディンガー方程式を考えています。

固有値

\(
\displaystyle E_n=-\frac{1}{2n^2},\;\;(n=1,2,\cdots,)
\)
です。

固有関数

\(
\begin{align}
\psi(x)=C \cdot e^{-x/n} x^l L_{n-1}^{(1)}(x)
\end{align}
\)
ここで,\(C\)は規格化定数, \(L_n^k(x)\)はラゲール倍多項式[5]で
\(
\begin{align}
L_0^k(x)&=1 \\
L_1^k(x)&=-x+k+1 \\
L_2^k(x)&=\frac{1}{2}[x^2-2(k+2)x+(k+1)(k+2)] \\
L_3^k(x)&=\frac{1}{6}[-x^3+3(k+3)x^2-3(k+2)(k+3)x+(k+1)(k+2)(k+3)]
\end{align}
\)
です。もちろん規格化定数をあらわに決めることが出来ますが、通常、この問題は3次元のシュレーディンガー方程式を解いた時の動径方向として出てくるので、その時の規格化は
\(
\displaystyle \int_0^\infty x^2 \psi(x)^2 dx =1
\)
で規格化されます。しかし、本稿の規格化は\(\displaystyle \int_0^\infty \psi(x)^2 dx =1\)
で規格化しているので、エネルギー固有値のみの比較を行います。

解法

\(x=0, x\to infty\)の漸近形を考えて、本当の解を
(\(x=0\)の漸近形)×(\(x=\infty\)の漸近形)×(未知関数)
と仮定します。これをシュレーディンガー方程式に代入すると未知関数がラゲール陪多項式だと分かります。

数値計算解と解析解との比較

数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[0,80]
基底関数の数(N)：200

エネルギー固有値

考察

クーロンポテンシャルの場合、\(x=\infty\)では波動関数は指数関数で減衰していきます。
このため、減衰がゆっくりになってしまい、sin関数でうまく表現できないために精度が落ちているのだと推測できます。
また、計算区間を十分に大きく取ると励起状態の表現はうまくいきますが、反対に基底状態の表現ができなくなります。なぜなら、多くの区間で波動関数はゼロですが、\(x=0\)の近傍だけに大きなピークを持つため、sin関数ではうまく表現できません。その兆候は上の数値計算でも見えてます。基底状態は2桁程度ですが、量子数の増加と共に1桁くらい精度が上がっています。
クーロンの場合、ラゲール関数を基底関数としてとる方が良いでしょう。

参考文献

[1]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, Gauss-Lobatto求積法 p.88
[2]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, ゼロ点に挟まれる区間の積分 p.131
[3]ランダウ＝リフシッツ,「量子力学１」第3刷, p81-84
[4]Abramowitz and Stegun, HANDBOOK OF MATHEMATICAL FUNCTIONS, p.446,478 http://people.math.sfu.ca/~cbm/aands/page_446.htm

Airy関数のゼロ点は
エアリー関数 Ai, Bi（ゼロ点）-Keisan
より22桁の精度で求めたものを用いています。
ちなみにそれらの値(Airy関数のゼロ点)は、

です。ゼロ点を0,1,2,…と、今回の計算の都合上0からインデックスを付けています。
もしかすると最後の1~2桁はあってないかもしれませんが、本稿では16桁まであっていればいいので、問題ありません。

[5]
Associated Laguerre Polynomial -wolfram mathworld式(22)-(25)

時間依存しないシュレーディンガー方程式を数値的に解くための、変分原理について述べていきます。
変分原理はエネルギー固有値の上限を与えます(厳密な解よりも変分原理で求めた解は必ず大きくなる)。
基底関数を適切に選べば高精度の結果が与えられます。ですが、基底関数をどのように選べばよいか？の指標は無く、経験則に頼らざるを得ない状況が出てきます。

ここでは、変分原理によってなぜエネルギー固有値が求まるのかを述べて行きます。

もしも変分原理より正しい解を得たければ、shooting methodと呼ばれる方法も推奨します。
恐らくこちらの方が色々なポテンシャルに対して有効ですが、
・計算速度が遅い
・発散の可能性がある
・変分原理よりも経験値が必要
です。

まとめ

区間[a,b]で定義された時間依存しないシュレーディンガー方程式
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+V(x)\right]\psi(x)=E\psi(x)
\)
の解である固有関数を
\(
\displaystyle \psi(x)=\sum_n c_n \varphi_n(x) \ \ …(6)
\)
の形で固定端条件(\(\psi(a)=\psi(b)=0\))の下で探します。
ここで、\(\varphi_n(x)\)は区間\([a,b]\)で正規直交化されたsin関数系
\(
\displaystyle \varphi_n(x)=\sqrt{\frac{2}{b-a}}\sin\left(\frac{n\pi}{b-a}(x-a)\right),\;\;\;(n=1,2,\cdots,N)
\)
です。この時、行列要素\(H_{ij}=\langle\varphi_i|-\frac{1}{2}\frac{d^2}{dx^2}+V(x)|\varphi_j\rangle\)は
\(
\begin{align}
H_{ij}&=K_{ij}+V_{ij} \\
&\hspace{1em}K_{ij}=\frac{1}{2}\left(\frac{j\pi}{b-a}\right)^2\delta_{ij} \\
&\hspace{1em}V_{ij}=\frac{1}{j}\sum_{m=2}^{M-1}\omega_m^{(GL)} \cos\left(\frac{\pi}{2}x_m^{(GL)}\right)
\sum_{n=0}^{j-1}(-1)^n \sin\left(\frac{i\pi}{2j}(x_m^{GL}+2n+1)\right)V(X_n^{(m)}) \\
&\hspace{2em}X_{n}^{(m)}=\frac{h}{2}(x_m^{(GL)}+2n+1)+a,\;\;h=\frac{b-a}{j}
\end{align}
\)
と求められます(\(j\ge i\)を推奨)。ここで、\(\omega_m^{(GL)},\ x_m^{(GL)}\)はM点のGauss-Lobatto求積法の区間[-1,1]における重みと求積点で、
\(
\displaystyle \omega_m=\frac{2}{M(M-1)[P_{M-1}(x_m)]^2},\ \ x_m\ne \pm 1
\)
であり、求積点は関数
\(
\displaystyle \frac{P_{M-1}(x)+P_{M}(x)}{x-1}
\)
のゼロ点です。\(P_{n}(x)\)は\(n\)次Legendre多項式を表します。

1. 解説
2. 時間依存から時間依存しないシュレーディンガー方程式へ
3. 間接法
   1. 行列要素の計算
   2. K_{nm}の計算
   3. V_{nm}の計算
   4. Gauss-Lobatto求積法による積分の計算
   5. ゼロ点に挟まれる区間の積分
4. 数値計算プログラム
5. 正規直交系を用いない場合
6. 研究分野での数値計算法について
7. 参考文献

計算の具体例は
時間依存しないシュレーディンガー方程式と変分原理 2/2 （計算例）をご覧ください。

[adsense1]

解説

対象とする問題を導出します。何はともあれ、時間依存シュレーディンガー方程式から出発します。

時間依存から時間依存しないシュレーディンガー方程式へ

時間依存シュレーディンガー方程式は
\(
\displaystyle i\frac{\partial \Psi(x,t)}{\partial t}=\hat{H}(x)\Psi(x,t)
\)
と記述されます。ここで、簡単ために原子単位系(\(\hbar=1, m=1\))を考えます。
変数分離の形で解を仮定します。
\(
\displaystyle \Psi(x,t)=\psi(x)U(t)
\)
代入して移行すると以下の式を得ます。

2番目の式の右辺\(E\)は何らかの定数です。
左辺は時間のみを含む式、真ん中の式は位置のみを含む式なので、いつどんな時でもこの関係式が成り立っていないといけないという条件からこれらはなんらかの定数でなければなりません。その定数を\(E\)と置きました。

すなわち、２つの式
\(
\begin{align}
i\frac{\partial U(t)}{\partial t}=E U(t)\;\;\; \cdots(1)\\
\hat{H}\psi(x) = E\psi(x)\;\;\; \cdots(2)
\end{align}
\)
が導けます。

\(t\)に関する式は\(\hat{H}(x)\)に依らず解けてしまい、
\(U(t)=e^{-i E t}\)(1)
です。位置に関する式は
\(
\hat{H}\psi(x) = E\psi(x)
\)(2)
を満たさなければなりません。この(2)が時間依存しないシュレーディンガー方程式と呼ばれているものです。
これを数値計算で解いていくことを考えます。

左から\(\psi^*\)を掛けて全空間で積分しますと、
\(
\begin{align}
\int \psi^* \hat{H} \psi dx – E \int \psi^* \psi dx = 0\;\;\; \cdots(3)
\end{align}
\)
という式を得ます。この問題は
条件\(\int \psi^* \psi dx=1\)の下で、\(\int \psi^* \hat{H} \psi dx\)の極値を求めよ、
という問いになります。
上記問題を考えた時、(3)と同一の式になります。

すなわち、原理的にはどんな\(\psi(x)\)を与えても\(E(=E[\psi])\)の値を計算できるわけです。
その無数に考えられる\(\psi\)の中で、特に(3)の解が停留する\(\psi\)、すなわち
\(
\displaystyle \delta \int \psi^* (\hat{H}-E) \psi dx = 0
\)
となる\(\psi\)を探せ、という問題になります。

↑がもしも停留する\(\psi\)が見付かれば、それはシュレーディンガー方程式と同一になるということは以下の通りに示せます。

\(
\displaystyle \delta \int \psi^* (\hat{H}-E) \psi dx =0 \;\;\;\cdots (4)
\)
厳密な\(\psi\)の変分に対して停留、すなわち\(\psi\to \psi+\delta \psi\)、もしくは複素平面で\(\frac{\pi}{2}\)ずれた方向\(\psi\to \psi+i\delta \psi\)に対して0でなければなりません。
(4)に対して２つの方向に対して変分を取ると、
\(
\begin{align}
\int (\delta \psi)^* (\hat{H}-E)\psi dx &+ \int \psi^* (\hat{H}-E)(\delta\psi) dx =0 \\
-i\int (\delta \psi)^* (\hat{H}-E)\psi dx &+ i\int \psi^* (\hat{H}-E)(\delta\psi) dx =0
\end{align}
\)
と2式が導けます。2式は変分をとった方向にかかわらず同時に満たされていなければなりません。同時に成立するためには
\(
(\hat{H}-E)\psi=0,\;\; \text{or}\;\; \psi^*(\hat{H}^{\dagger}-E^*)=0
\)
を満たしている必要があります。これは時間依存しないシュレーディンガー方程式と一致します。

以上をまとめますと、

厳密な\(\psi\)の変分はシュレーディンガー方程式に一致する
↓
近似的に\(\psi\)を変分するとシュレーディンガー方程式の近似的な解に帰着されるだろう
↓
近似的に\(\psi\)を構成し、変分問題を解く

代表的な方法として、
手法1)直接法…\(\psi\)の具体的な形を変分パラメータと共に与える
手法2)間接法…変分パラメータとしてある正規直交基底関数系を採用する
の２つがありますが、数値計算で使われる間接法を説明します。

間接法

間接法による変分原理は、

• 固有値の上限を与える（変分原理によるエネルギー固有値は必ず厳密なエネルギー固有値よりも大きくなる）
• 基底関数の数を増やすほど精度は上がる(完全系の場合)

という特性があります。

さて、今解きたい問題は
条件
\(
\displaystyle \int \psi^* \psi dx =1
\)
の下で
\(
\displaystyle \int \psi^* \hat{H} \psi dx
\)
の極値を与える\(\psi\)を探すこと、です。

すなわち
\(
\displaystyle \int \psi^* \hat{H} \psi dx – E \int \psi^* \psi dx =0 \ \ …(5)
\)
を考えて変分します。求めたい波動関数は
\(
\displaystyle \psi(x)=\sum_n c_n \varphi_n(x) \ \ …(6)
\)
と展開できる、と考えます。ここで、\(c_n\)は変分パラメータ、\(\varphi_n(x)\)は区間[a,b]で定義されている正規直交関数系です。正規直交関数系\(\{\varphi_n(x)\}\)は以下の性質を持ちます。
\(
\displaystyle \int_a^b \varphi_n(x) \varphi_m(x)dx =\delta_{nm}
\)
この制約が無くても変分は可能ですが、以降の式が簡略になるので、正規直交関数だけを考えます。

(6)を(5)に代入すると、
\(
\begin{align}
\sum_{n}\sum_{m} c_n^* c_m \left[H_{nm}-E \delta_{nm}\right]=0 \\
\end{align}\ \ …(7)
\)
なります。ここで、
\(
\begin{align}
H_{nm}&=\int_a^b \varphi_n(x) \hat{H} \varphi_m(x)dx
\end{align}
\)
とおきました。(7)式を満たす係数\(\{c_n\}\)の内、自明な解(\(c_n=0\ (for\ all\ n)\))はすぐ見つかります。しかし、この解は\(\psi(x)=0\)であり、条件\(
\displaystyle \int \psi^* \psi dx =1\)を満たしません。なので解としては不適切です。

では非自明な解を見つけましょう。(7)式の解を探すため、極値を探します。今、係数の組を変分パラメータとみなしているので、(変分パラメータで微分したもの)=0を計算します。すなわち
\(
\displaystyle \frac{\partial}{\partial c_n^*} (for\ all\ n)
\)
を(7)式に作用させます。すると、
\(
\begin{align}
\sum_{n}\sum_{m} \left[H_{nm}-E\delta_{nm}\right]c_m=0
\end{align}
\)
となります。\(n,m\)を行列の行、列ととらえれば、

\(
\begin{align}
\left(
\begin{array}{cccc}
H_{11} & H_{12} & \cdots & H_{1N}\\
H_{21} & H_{22} & \cdots & H_{2N}\\
\ddots & \ddots & \ldots & \ddots \\
H_{N1} & H_{N2} & \cdots & H_{NN}
\end{array}
\right)
\left(
\begin{array}{c}
c_{1} \\
c_{2} \\
\ddots \\
c_{N}
\end{array}
\right)
=
E
\left(
\begin{array}{c}
c_{1} \\
c_{2} \\
\ddots \\
c_{N}
\end{array}
\right)
\end{align}
\)

となるわけです。ということは、左辺の正方行列を対角化すれば右辺のE,すなわち固有値が求まる、という事になります。

行列要素の計算

行列を対角化するためには行列要素\(H_{nm}\)が分かっていないとなりません。
これからこの行列要素を計算していきます。

ハミルトニアンが
\(
\displaystyle \hat{H}=-\frac{1}{2}\frac{d^2 }{d x^2} + V(x)
\)
として表現されている場合、行列要素は
\(
\begin{align}
H_{nm}&=K_{nm}+V_{nm} \\
&\hspace{3em} K_{nm}=-\frac{1}{2}\int_a^b \varphi_n(x)\frac{d^2}{dx^2} \varphi_m(x)dx \\
&\hspace{3em} V_{nm}=\int_a^b \varphi_n(x)V(x) \varphi_m(x)dx
\end{align}
\)
と書き表され、これらを数値計算で求めます。

\(K_{nm}\)の計算

まず、微分を含んだ
\(
\displaystyle K_{nm}=-\frac{1}{2}\int_a^b \varphi_n(x)\frac{d^2}{dx^2} \varphi_m(x)dx
\)
の項を考えます。微分は数値計算で行いません。
というのも正規直交関数系はこちらで用意する知っている関数系なので、求めることが出来てしまうからです。
多くの正規直交関数系には漸化式と微分方程式が存在します。一番簡単な基底としてsin関数系を考えてみましょう。
区間\([a,b]\)で正規直交化されたsin関数系は
\(
\displaystyle \varphi_n(x)=\sqrt{\frac{2}{b-a}}\sin\left(\frac{n\pi}{b-a}(x-a)\right),\;\;\;(n=1,2,\cdots,N)
\)
と書き表せます。sin関数なので、2階微分はもちろん
\(
\displaystyle \frac{d^2}{dx^2}\varphi_n(x)=-\left(\frac{n\pi}{b-a}\right)^2\varphi_n(x)
\)
を満たします。これを積分の中に代入して、
\(
\begin{align}
K_{nm}&=-\frac{1}{2}\int_a^b \varphi_n(x)\frac{d^2}{dx^2} \varphi_m(x)dx \\
&=\frac{1}{2}\left(\frac{n\pi}{b-a}\right)^2\int_a^b \varphi_n(x) \varphi_m(x)dx \\
&=\frac{1}{2}\left(\frac{n\pi}{b-a}\right)^2\delta_nm
\end{align}
\)
となります。積分を計算することなく求める事が出来ました。

より一般には一回微分の存在しない形、もしくは漸化式によって手計算で微分を含む積分を片付けてしまったり、部分積分を用いて何とか計算します。
正規直交系であれば、うまく整理することによって誤差が全く入らず、かつ高速に計算できます。

\(V_{nm}\)の計算

さて、残る問題は
\(
\displaystyle V_{nm}=\int_a^b \varphi_n(x)V(x) \varphi_m(x)dx
\)
の計算です。基底関数の次数が低い場合、この計算は何も問題がありません。
調和ポテンシャル\(V(x)=x^2\)の時、\(n=1,m=2\)の時の被積分関数は

と非常になだらかですが、\(n=5,m=99\)の時の被積分関数は

となります。なので細かい分点をとることになり、非常に積分が難しいです。

離散フーリエ変換によって求められそうな気もしますが、周期境界条件が満たされていないことは明らかなのであきらめましょう。
有限区間で早く振動する関数の積分は難しいです。二重指数関数型数値積分も振動する関数は苦手です。

こういった場合の計算方法として、
・ゼロ点の位置が分かっている場合、そこで区間を分割して積分する
という直観的な方法があります[2]。
ゼロ点の位置が分かっていれば、その間の被積分関数の振る舞いはシンプルな形になるので滑らかな関数として考えられます。

また、端点での値がゼロだと分かっている場合、Gauss-Lobatto求積法が非常に有用です。

Gauss-Lobatto求積法による積分の計算

Gauss-Lobatto求積法はGauss-Legendre求積法と同じく被積分関数を多項式で近似します[1]。
Gauss-Legendre求積法と異なる点は端点で分点を持つということです。端点を明示的に書けば、積分は
\(
\displaystyle \int_{-1}^1 f(x)dx\sim \frac{2}{N(N-1)}(f(-1)+f(1))+\sum_{i=2}^{N-1}\omega_i f(x_i)
\)
と書けます。ここで、\(\omega_i,x_i\)はGauss-Lobatto求積法における重み、求積点です。
Gauss-Lobatto求積法の重みは
\(
\displaystyle \omega_i=\frac{2}{N(N-1)[P_{N-1}(x_i)]^2},\ \ x_i\ne \pm 1
\)
であり、求積点は
\(
\displaystyle \frac{P_{N-1}(x)+P_{N}(x)}{x-1}
\)
のゼロ点です。\(P_{n}(x)\)は\(n\)次Legendre多項式を表します。

Gauss-Lobatto求積法は
\(f(\pm 1)\)が既知の値(特に0)を持つ場合
に便利なことが分かります。
関数\(f(\pm 1)\)がゼロであれば、その点を計算する必要性がなくなりますし、見かけ上の特異点であってもこちらで値を指定すれば参照されることはなく、計算できないという状況に陥りません。

ゼロ点に挟まれる区間の積分

ゼロ点に挟まれる区間の積分は、結局以下の式になります[2]。
\(
\displaystyle \varphi_j(x)=\sqrt{\frac{2}{b-a}}\sin\left(\frac{j\pi}{b-a}\right)
\)
とすると、積分は
\(
\begin{align}
&\int_a^b \varphi_i(x) V(x) \varphi_j(x) dx \\
&=\sum_{n=0}^{j-1} \int_{x_n}^{x_{n+1}} \varphi_i(x) V(x) \varphi_j(x)dx \\
&\approx \sum_{n=0}^{j-1}\sum_{m=2}^{M-1}\frac{h}{2} \omega_m^{(GL)}\varphi_i(X_n^{(m)}) V(X_n^{(m)}) \varphi_j(X_n^{(m)}) \\
&=\frac{h}{2}\sum_{m=2}^{M-1}\omega_m^{(GL)}\varphi_j(X_0^{(m)})S_j^{(m)} \\
\end{align}
\)
ここで、
\(
\begin{align}
&x_n=nh+a,\ h=\frac{b-a}{j},\ (n=0,1,\cdots,j) \\
&X_n^{(m)}=\frac{h}{2}x_m^{(GL)}+\frac{x_{n+1}+x_n}{2} \\
&X_{n+1}^{(m)}=X_n^{(m)}+h \\
&S_j^{(m)}=\sum_{n=0}^{j-1}(-1)^n \varphi_i(X_n^{(m)})V(X_n^{(m)})
\end{align}
\)
と置きました。
\(x_m^{(GL)},\ \omega_m^{(GL)}\)は区間\([-1,1]\)でのM点Gauss-Lobatto求積法の求積点と重みです。
計算を可能な限り減らすため、\(\varphi_j(x)\)の周期性を用いています。

数値計算プログラム

行列要素を組み立てた後は適当なルーチンを用いて対角化します。
今回の場合、基底関数をsin関数に選んだため、強制的に固定端条件が課されます。
なので、この基底関数系を用いるといかなる問題も端点\(a,b\)に無限に高いポテンシャルの壁がある、と読み替えることが出来ます。
よって行列は対称行列、エルミートです。故に固有値は必ず実数です。

この問題を解く場合、実対称行列を対角化するルーチン、lapackのdsyevdを用いるのが良いでしょう。
対角化のプログラムに関する詳細は対角化へどうぞ。

以下のプログラムは行列要素を上記手法で作り、対角化し、得られた波動関数を規格化し、出力するものです。

[adsense2]

コンパイルと実行は

などとしてください。lapackを用いますので、それと一緒にコンパイルしてください。

ラグランジュの未定乗数について

ラグランジュの未定乗数は特に物理的な意味を持たない魔法の変数、として置きますが、今回の場合は未定乗数がエネルギー固有値というちゃんとした意味を持つのです。

正規直交系を用いない場合

\(
\begin{align}
\sum_{n}\sum_{m} c_n^* c_m \left[H_{nm}-E I_{nm}\right]=0 \\
\sum_{n}\sum_{m} c_n^* c_m \left[J_{nm} H_{nm}-E \right]=0
\end{align}\ \ …(7)
\)
となります。ここで、
\(
\begin{align}
H_{nm}&=\int_a^b \varphi_n(x) \hat{H} \varphi_m(x)dx\\
J_{nm}&=I_{nm}^{-1}\\
I_{nm}&=\int_a^b \varphi_n(x) \varphi_m(x)dx
\end{align}
\)
と置きました。行列の形では、
\(
\begin{align}
\left(
\begin{array}{cccc}
J_{11}H_{11} & J_{12}H_{12} & \cdots & J_{1N}H_{1N}\\
J_{21}H_{21} & J_{22}H_{22} & \cdots & J_{2N}H_{2N}\\
\ddots & \ddots & \ldots & \ddots \\
J_{N1}H_{N1} & J_{N2}H_{N2} & \cdots & J_{NN}H_{NN}
\end{array}
\right)
\left(
\begin{array}{c}
c_{1} \\
c_{2} \\
\ddots \\
c_{N}
\end{array}
\right)
=
E
\left(
\begin{array}{cccc}
1 & 0 & \cdots & 0\\
0 & 1 & \cdots & 0\\
\ddots & \ddots & \ldots & \ddots \\
0 & 0 & \cdots & 1
\end{array}
\right)
\left(
\begin{array}{c}
c_{1} \\
c_{2} \\
\ddots \\
c_{N}
\end{array}
\right)
\end{align}
\)
と書けます。

\(
\begin{align}
\sum_{n}\sum_{m} c_n^* c_m \left[H_{nm}-E I_{nm}\right]=0 \\
\sum_{n}\sum_{m} c_n^* c_m \left[I_{nm}^{-1} H_{nm}-E \right]=0
\end{align}
\)

研究分野での数値計算法について

実際の研究の場では対角化はしますが、上記方法によって行列要素を作ることはしません。遅いからです。
特別な基底関数を用いると行列要素\(H_{nm}\)が1~2項、しかも非常に簡単な式に置き換えることが出来ます。精度も速度も上記方法以上です。
この計算方法に関してはこれ以上は述べることはしませんが、こういった方法も存在する、とだけ述べておきます。

参考文献

[1]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, Gauss-Lobatto求積法 p.88
[2]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, ゼロ点に挟まれる区間の積分 p.131
[3]ランダウ＝リフシッツ,「量子力学１」第3刷, p81-84