シンプルQUADPACK

QUADPACKのコード(http://www.netlib.org/quadpack/)は優秀ですが、2000行近くあって色々いじる際に面倒です(最速・高精度の数値積分)。

コードを覗くと、求積法の点数だけが違うプログラムがあるので長いことに気が付きます。
なのでコード量を減らしましょう。

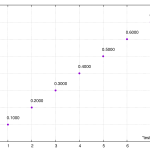
使用する積分方法を20-41点ガウス求積法(key=4)に限定しました。key=4を選んだ理由は、最速・高精度の数値積分の結果から推測しました。

key=2の低次の方法(10-21点)であると滑らかな関数でも評価回数が多くなる反面、不連続点があっても少なく済みます。
key=6の高次の方法(30-61点)であると滑らかな関数で評価回数が少なくなる反面、不連続点があると多くなります。

QUADPACKにはkey=1,2,3,4,5,6のどれかを選べますが、基本的に滑らかな関数の積分を行うことが多いので若干高次のkey=4を選びました。

350行程度にまで減らし、ルーチンを一つ無くました。変更箇所が怖い方は、オリジナルのものを使用してください。

コードの変更をした結果、計算結果が違くなるなど問題が起こる場合、原因は私にあります。
著作者とは関係ありませんので、その点はよろしくお願いします。

program main
implicit none
double precision::a,b,err,Rtol,Atol
double precision::s
double precision,external::f

a=0d0
b=1d0
Rtol=1d-4
Atol=1d-16
call dqag4(f,a,b,Rtol,Atol,s,err)
write(6,*)s,err

stop
end program main

function f(x)
implicit none
double precision::x
double precision::f

f=sqrt(x)

return
end function f

!===================================

subroutine dqag4(f,a,b,Rtol,Atol,s,abserr)
implicit none
double precision,intent(in)::a,b,Rtol,Atol
double precision,intent(out)::abserr
double precision,intent(out)::s
double precision,external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
! f : Function
! a,b : Integration range [a,b]
! Rtol : Require relative error
! Atol : Require absolute error
! s : Numerical integration result
! abserr : Estimated error of integration
!
integer::neval,limit,lenw,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
double precision,allocatable::rlist(:)

!=============
limit=1000
! limit increase --> converge
!=============

s=0d0
lenw=limit*4
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit))
allocate(elist(1:limit),rlist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=0d0

ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

call dqage(f,a,b,Atol,Rtol,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork,alist,blist,rlist,elist)
return
end subroutine dqag4

subroutine dqage(f,a,b,Atol,Rtol,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
implicit none
integer,intent(in)::limit
integer,intent(inout)::count
double precision,intent(in)::a,b,Atol,Rtol
double precision,intent(inout)::alist(1:limit),blist(1:limit),elist(1:limit)
double precision,intent(inout)::rlist(1:limit)
integer,intent(out)::ier,neval,last,iord(1:limit)
double precision,intent(out)::abserr
double precision,intent(out)::result
double precision,external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/07/07 modified by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

integer iroff1,iroff2,k,maxerr,nrmax,igt,igk
double precision::a1,a2,b1,b2,defabs,&
defab1,defab2,dmax1,epmach,errbnd,errmax,&
error1,error2,erro12,errsum,uflow,resabs
double precision::area,area1,area12,area2

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = 0d0
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = 0d0
elist(1) = 0.0d+00
iord(1) = 0
if(Atol.le.0.0d+00.and.&
Rtol.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41(f,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(Atol,Rtol*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41(f,a1,b1,area1,error1,resabs,defab1,count)
call dqk41(f,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(Atol,Rtol*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage

subroutine dqk41(f,a,b,result,abserr,resabs,resasc,count)
implicit none
double precision,intent(in)::a,b
integer,intent(inout)::count
double precision,intent(out)::abserr,resabs,resasc
double precision,intent(out)::result
double precision,external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/07/07 modified by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

double precision::absc,centr,dhlgth,dmax1,dmin1,&
epmach,hlgth,uflow
double precision::resg,resk,reskh,fval1,fval2,fc,fsum
integer::j,jtw,jtwm1
double precision::fv1(1:20),fv2(1:20)
double precision::xgk(1:21),wgk(1:21),wg(1:10)

data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /

data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /

data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
fc = f(centr) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
fval1 = f(centr-absc) ! *************
fval2 = f(centr+absc) ! *************
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
fval1 = f(centr-absc) ! *************
fval2 = f(centr+absc) ! *************
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine dqk41

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
implicit none
integer,intent(in)::limit,last
integer,intent(inout)::maxerr,iord(1:limit),nrmax
double precision,intent(inout)::elist(1:limit)
double precision::ermax,errmax,errmin
integer::i,ibeg,ido,isucc,j,jbnd,jupbn,k,igt,igt1,igt2
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer,intent(in)::level,nerr,nmess
character ( len = * ),intent(in)::xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————

実軸上、複素関数でkey=4の場合

▼ここクリックでこの場に展開

program main
implicit none
double precision::a,b,err,Rtol,Atol
complex(kind(0d0))::s
complex(kind(0d0)),external::f

a=0d0
b=1d0
Rtol=1d-10
Atol=1d-16
call cqag4(f,a,b,Rtol,Atol,s,err)
write(6,*)s,err

stop
end program main

function f(x)
implicit none
double precision::x
complex(kind(0d0))::f

!f=exp(dcmplx(0d0,1d0)*100d0*x)
f=sqrt(x)+dcmplx(0d0,1d0)*x*x

return
end function f

!===================================

subroutine cqag4(f,a,b,Rtol,Atol,s,abserr)
implicit none
double precision,intent(in)::a,b,Rtol,Atol
double precision,intent(out)::abserr
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
! f : Function
! a,b : Integration range [a,b]
! Rtol : Require relative error
! Atol : Require absolute error
! s : Numerical integration result
! abserr : Estimated error of integration
!
integer::neval,limit,lenw,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)
lenw=limit*4
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit))
allocate(elist(1:limit),rlist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

call cqage(f,a,b,Atol,Rtol,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork,alist,blist,rlist,elist)
return
end subroutine cqag4

subroutine cqage(f,a,b,Atol,Rtol,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
implicit none
integer,intent(in)::limit
integer,intent(inout)::count
double precision,intent(in)::a,b,Atol,Rtol
double precision,intent(inout)::alist(1:limit),blist(1:limit),elist(1:limit)
complex(kind(0d0)),intent(inout)::rlist(1:limit)
integer,intent(out)::ier,neval,last,iord(1:limit)
double precision,intent(out)::abserr
complex(kind(0d0)),intent(out)::result
complex(kind(0d0)),external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/07/07 modified by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

integer::iroff1,iroff2,k,maxerr,nrmax,igt,igk
double precision::a1,a2,b1,b2,defabs,&
defab1,defab2,dmax1,epmach,errbnd,errmax,&
error1,error2,erro12,errsum,uflow,resabs
complex(kind(0d0))::area,area1,area12,area2

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(Atol.le.0.0d+00.and.&
Rtol.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call cqk41(f,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(Atol,Rtol*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call cqk41(f,a1,b1,area1,error1,resabs,defab1,count)
call cqk41(f,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(Atol,Rtol*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine cqage

subroutine cqk41(f,a,b,result,abserr,resabs,resasc,count)
implicit none
double precision,intent(in)::a,b
integer,intent(inout)::count
double precision,intent(out)::abserr,resabs,resasc
complex(kind(0d0)),intent(out)::result
complex(kind(0d0)),external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/07/07 modified by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

double precision::absc,centr,dhlgth,dmax1,dmin1,&
epmach,hlgth,uflow
complex(kind(0d0))::resg,resk,reskh,fval1,fval2,fc,fsum
integer::j,jtw,jtwm1
complex(kind(0d0))::fv1(1:20),fv2(1:20)
double precision::xgk(1:21),wgk(1:21),wg(1:10)

data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /

data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /

data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
fc = f(centr) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
fval1 = f(centr-absc) ! *************
fval2 = f(centr+absc) ! *************
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
fval1 = f(centr-absc) ! *************
fval2 = f(centr+absc) ! *************
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine cqk41

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
implicit none
integer,intent(in)::limit,last
integer,intent(inout)::maxerr,iord(1:limit),nrmax
double precision,intent(inout)::elist(1:limit)
double precision::ermax,errmax,errmin
integer::i,ibeg,ido,isucc,j,jbnd,jupbn,k,igt,igt1,igt2
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer,intent(in)::level,nerr,nmess
character ( len = * ),intent(in)::xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————

２次元実軸上、複素関数でkey=4の場合

▼ここクリックでこの場に展開

program main
implicit none
double precision::xa,xb,ya,yb,xeps,yeps
complex(kind(0d0))::s
complex(kind(0d0)),external::f

xa=1d0
xb=5d0
ya=1d0
yb=3d0
xeps=1d-10
yeps=1d-10
call dqag42(f,xa,xb,ya,yb,xeps,yeps,s)
write(6,*)s

stop
end program main

function f(x,y)
implicit none
double precision::x,y
complex(kind(0d0))::f

f=exp(-dcmplx(0d0,1d0)*sqrt(x)*y)+sin(50d0*y)

return
end function f

!===================================

subroutine dqag42(f,a,b,ya,yb,eps,yeps,s)
implicit none
double precision,intent(in)::a,b,eps,ya,yb,yeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

call dqage2(f,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,ya,yb,yeps)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

! write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag42

subroutine dqage2(f,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,ya,yb,yeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/29 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,ya,yb,yeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk412(f,a,b,result,abserr,defabs,resabs,count,ya,yb,yeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk412(f,a1,b1,area1,error1,resabs,defab1,count,ya,yb,yeps)
call dqk412(f,a2,b2,area2,error2,resabs,defab2,count,ya,yb,yeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage2

subroutine dqk412(f,a,b,result,abserr,resabs,resasc,count,ya,yb,yeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,ya,yb,yeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
call dqag4y(f,centr,ya,yb,yeps,fc,count)
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4y(f,centr-absc,ya,yb,yeps,fval1,count)
call dqag4y(f,centr+absc,ya,yb,yeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4y(f,centr-absc,ya,yb,yeps,fval1,count)
call dqag4y(f,centr+absc,ya,yb,yeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)

return
end subroutine dqk412

subroutine dqag4y(f,x,a,b,eps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,a,b,eps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
!count = 0

call dqagey(f,x,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

!write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag4y

subroutine dqagey(f,x,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41y(f,x,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41y(f,x,a1,b1,area1,error1,resabs,defab1,count)
call dqk41y(f,x,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqagey

subroutine dqk41y(f,x,a,b,result,abserr,resabs,resasc,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
fc = f(x,centr) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,centr-absc)
fval2 = f(x,centr+absc)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,centr-absc)
fval2 = f(x,centr+absc)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine dqk41y

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
double precision elist,ermax,errmax,errmin
integer i,ibeg,ido,iord,isucc,j,jbnd,jupbn,k,last,limit,maxerr,&
nrmax,igt,igt1,igt2
dimension elist(last),iord(last)
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer::level,nerr,nmess
character ( len = * ) xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————

３次元実軸上、複素関数でkey=4の場合

▼ここクリックでこの場に展開

program main
implicit none
double precision::xa,xb,ya,yb,za,zb,xeps,yeps,zeps
complex(kind(0d0))::s
complex(kind(0d0)),external::f

xa=1d0
xb=5d0
ya=1d0
yb=3d0
za=0d0
zb=2d0
xeps=1d-10
yeps=1d-10
zeps=1d-10
call dqag43(f,xa,xb,ya,yb,za,zb,xeps,yeps,zeps,s)
write(6,*)s

stop
end program main

function f(x,y,z)
implicit none
double precision::x,y,z
complex(kind(0d0))::f

f=(exp(-dcmplx(0d0,1d0)*sqrt(x)*y)+sin(5d0*y))*exp(dcmplx(0d0,1d0)*z*z)

return
end function f

!===================================

subroutine dqag43(f,a,b,ya,yb,za,zb,eps,yeps,zeps,s)
implicit none
double precision,intent(in)::a,b,eps,ya,yb,yeps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

call dqage3(f,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,ya,yb,yeps,za,zb,zeps)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag43

subroutine dqage3(f,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,ya,yb,yeps,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk413(f,a,b,result,abserr,defabs,resabs,count,ya,yb,yeps,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk413(f,a1,b1,area1,error1,resabs,defab1,count,ya,yb,yeps,za,zb,zeps)
call dqk413(f,a2,b2,area2,error2,resabs,defab2,count,ya,yb,yeps,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage3

subroutine dqk413(f,a,b,result,abserr,resabs,resasc,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,ya,yb,yeps,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
call dqag4yz(f,centr,ya,yb,yeps,za,zb,zeps,fc,count)
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag4yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag4yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)

return
end subroutine dqk413

subroutine dqag4yz(f,x,a,b,eps,za,zb,zeps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,a,b,eps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
!count = 0

call dqageyz(f,x,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,za,zb,zeps)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

!write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag4yz

subroutine dqageyz(f,x,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41yz(f,x,a,b,result,abserr,defabs,resabs,count,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41yz(f,x,a1,b1,area1,error1,resabs,defab1,count,za,zb,zeps)
call dqk41yz(f,x,a2,b2,area2,error2,resabs,defab2,count,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqageyz

subroutine dqk41yz(f,x,a,b,result,abserr,resabs,resasc,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
!fc = f(x,centr) ! *************
call dqag4z(f,x,centr,za,zb,zeps,fc,count)

resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
!fval1 = f(x,centr-absc)
!fval2 = f(x,centr+absc)
call dqag4z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag4z(f,x,centr+absc,za,zb,zeps,fval2,count)

fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
!fval1 = f(x,centr-absc)
!fval2 = f(x,centr+absc)
call dqag4z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag4z(f,x,centr+absc,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
!count=count+41
return
end subroutine dqk41yz

subroutine dqag4z(f,x,y,a,b,eps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,y,a,b,eps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
!count = 0

call dqagez(f,x,y,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

!write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag4z

subroutine dqagez(f,x,y,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,y
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41z(f,x,y,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41z(f,x,y,a1,b1,area1,error1,resabs,defab1,count)
call dqk41z(f,x,y,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqagez

subroutine dqk41z(f,x,y,a,b,result,abserr,resabs,resasc,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,y
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
fc = f(x,y,centr) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,y,centr-absc)
fval2 = f(x,y,centr+absc)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,y,centr-absc)
fval2 = f(x,y,centr+absc)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine dqk41z

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
double precision elist,ermax,errmax,errmin
integer i,ibeg,ido,iord,isucc,j,jbnd,jupbn,k,last,limit,maxerr,&
nrmax,igt,igt1,igt2
dimension elist(last),iord(last)
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer::level,nerr,nmess
character ( len = * ) xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————

key=4, 複素平面上の積分

▼ここクリックでこの場に展開

program main
implicit none
double precision::Rtol,Atol,err
complex(kind(0d0))::a,b,s
complex(kind(0d0)),external::f

a=dcmplx(0d0,0d0)
b=dcmplx(1d0,1d0)
Rtol=1d-12
Atol=1d-16
call zqag4(f,a,b,Rtol,Atol,s,err)
write(6,*)s,err

stop
end program main

function f(x)
implicit nonex
complex(kind(0d0))::x
complex(kind(0d0))::f

f=x**(-0.5d0)

return
end function f

!===================================

subroutine zqag4(f,a,b,Rtol,Atol,s,abserr)
implicit none
complex(kind(0d0)),intent(in)::a,b
double precision,intent(in)::Rtol,Atol
double precision,intent(out)::abserr
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
! f : Function
! a,b : Integration range [a,b]
! Rtol : Require relative error
! Atol : Require absolute error
! s : Numerical integration result
! abserr : Estimated error of integration
!
integer::neval,limit,lenw,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
complex(kind(0d0))::eth,d
double precision::rmax

!=============
limit=1000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)
lenw=limit*4
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit))
allocate(elist(1:limit),rlist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

d=b-a
eth=exp(dcmplx(0d0,1d0)*atan2(imag(d),dble(d)))
rmax=abs(d)
call zqage(f,0d0,rmax,eth,a,Atol,Rtol,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)
s=s*eth

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork,alist,blist,rlist,elist)
return
end subroutine zqag4

subroutine zqage(f,a,b,eth,z0,Atol,Rtol,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
implicit none
integer,intent(in)::limit
integer,intent(inout)::count
double precision,intent(in)::a,b,Atol,Rtol
complex(kind(0d0)),intent(in)::eth,z0
double precision,intent(inout)::alist(1:limit),blist(1:limit),elist(1:limit)
complex(kind(0d0)),intent(inout)::rlist(1:limit)
integer,intent(out)::ier,neval,last,iord(1:limit)
double precision,intent(out)::abserr
complex(kind(0d0)),intent(out)::result
complex(kind(0d0)),external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/08/21 edited by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

integer::iroff1,iroff2,k,maxerr,nrmax,igt,igk
double precision::a1,a2,b1,b2,defabs,&
defab1,defab2,dmax1,epmach,errbnd,errmax,&
error1,error2,erro12,errsum,resabs,uflow
complex(kind(0d0))::area,area1,area12,area2

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(Atol.le.0.0d+00.and.&
Rtol.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call zqk41(f,a,b,eth,z0,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(Atol,Rtol*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call zqk41(f,a1,b1,eth,z0,area1,error1,resabs,defab1,count)
call zqk41(f,a2,b2,eth,z0,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(Atol,Rtol*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine zqage

subroutine zqk41(f,a,b,eth,z0,result,abserr,resabs,resasc,count)
implicit none
double precision,intent(in)::a,b
integer,intent(inout)::count
complex(kind(0d0)),intent(in)::eth,z0
double precision,intent(out)::abserr,resabs,resasc
complex(kind(0d0)),intent(out)::result
complex(kind(0d0)),external::f

!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2018/08/21 edited by sikino, http://slpr.sakura.ne.jp/qp/
! 2019/02/10 modified by sikino

double precision::absc,centr,dhlgth,dmax1,dmin1,&
epmach,hlgth,uflow
complex(kind(0d0))::resg,resk,reskh,fval1,fval2,fc,fsum
integer::j,jtw,jtwm1
complex(kind(0d0))::fv1(1:20),fv2(1:20)
double precision::xgk(1:21),wgk(1:21),wg(1:10)

data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
fc = f((centr)*eth+z0) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
fval1 = f((centr-absc)*eth+z0) ! *************
fval2 = f((centr+absc)*eth+z0) ! *************
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
fval1 = f((centr-absc)*eth+z0) ! *************
fval2 = f((centr+absc)*eth+z0) ! *************
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine zqk41

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
implicit none
integer,intent(in)::limit,last
integer,intent(inout)::maxerr,iord(1:limit),nrmax
double precision,intent(inout)::elist(1:limit)
double precision::ermax,errmax,errmin
integer::i,ibeg,ido,isucc,j,jbnd,jupbn,k,igt,igt1,igt2
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer,intent(in)::level,nerr,nmess
character ( len = * ),intent(in)::xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————
Key=1の場合
（7-15点ガウス求積法）
・不連続性や、端点特異性がある時に有利です。

▼ここクリックでこの場に展開

program main
implicit none
double precision::a,b,s,eps
double precision,external::f

a=0d0
b=1d0
eps=1d-10
call dqag1(f,a,b,eps,s)
write(6,*)s

stop
end program main

function f(x)
implicit none
double precision::f,x

f=x**(-0.5d0)

return
end function f

!============================

subroutine dqag1(f,a,b,eps,s)
implicit none
double precision,intent(in)::a,b,eps
double precision,intent(out)::s
double precision,external::f
!
! Quadpack integration package, using key=1
! (Gauss quadrature with 7-15 points)
!
integer::neval,limit,lenw,last,ier,l1,l2,l3,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::work(:)
double precision::epsabs,abserr

!=============
limit=1000
! limit increase --> converge
!=============

s=0d0
lenw=limit*4
allocate(iwork(1:limit),work(1:lenw))
epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

l1 = limit+1
l2 = limit+l1
l3 = limit+l2
call dqage(f,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,work(1),work(l1),work(l2),work(l3),iwork,last,count)
lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail
write(6,*)count,ier ! Number of times called integrand function
if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork,work)
return
end subroutine dqag1

subroutine dqage(f,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
!***author piessens,robert,appl. math. & progr. div. - k.u.leuven
! de doncker,elise,appl. math. & progr. div - k.u.leuven
! modified by sikino, 2018/07/09 yyyy/mm/dd
! (http://slpr.sakura.ne.jp/qp)
double precision a,abserr,alist,area,area1,area12,area2,a1,a2,b,&
blist,b1,b2,dabs,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,f,&
resabs,result,rlist,uflow
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit),&
rlist(limit)
external f
epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = 0.0d+00
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = 0.0d+00
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk15(f,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*dabs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk15(f,a1,b1,area1,error1,resabs,defab1,count)
call dqk15(f,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(dabs(rlist(maxerr)-area12).le.0.1d-04*dabs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*dabs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(dabs(a1),dabs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(dabs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage

subroutine dqk15(f,a,b,result,abserr,resabs,resasc,count)
!***author piessens,robert,appl. math. & progr. div. - k.u.leuven
! de doncker,elise,appl. math. & progr. div - k.u.leuven
! modified by sikino, 2018/07/09 yyyy/mm/dd
! (http://slpr.sakura.ne.jp/qp)
double precision a,absc,abserr,b,centr,dabs,dhlgth,dmax1,dmin1,&
epmach,f,fc,fsum,fval1,fval2,fv1,fv2,hlgth,resabs,resasc,&
resg,resk,reskh,result,uflow,wg,wgk,xgk
integer j,jtw,jtwm1,count
external f
!
dimension fv1(7),fv2(7),wg(4),wgk(8),xgk(8)
data wg ( 1) / 0.129484966168869693270611432679082d0 /
data wg ( 2) / 0.279705391489276667901467771423780d0 /
data wg ( 3) / 0.381830050505118944950369775488975d0 /
data wg ( 4) / 0.417959183673469387755102040816327d0 /
!
data xgk ( 1) / 0.991455371120812639206854697526329d0 /
data xgk ( 2) / 0.949107912342758524526189684047851d0 /
data xgk ( 3) / 0.864864423359769072789712788640926d0 /
data xgk ( 4) / 0.741531185599394439863864773280788d0 /
data xgk ( 5) / 0.586087235467691130294144838258730d0 /
data xgk ( 6) / 0.405845151377397166906606412076961d0 /
data xgk ( 7) / 0.207784955007898467600689403773245d0 /
data xgk ( 8) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.022935322010529224963732008058970d0 /
data wgk ( 2) / 0.063092092629978553290700663189204d0 /
data wgk ( 3) / 0.104790010322250183839876322541518d0 /
data wgk ( 4) / 0.140653259715525918745189590510238d0 /
data wgk ( 5) / 0.169004726639267902826583426598550d0 /
data wgk ( 6) / 0.190350578064785409913256402421014d0 /
data wgk ( 7) / 0.204432940075298892414161999234649d0 /
data wgk ( 8) / 0.209482141084727828012999174891714d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = dabs(hlgth)
fc = f(centr) !****************
resg = fc*wg(4)
resk = fc*wgk(8)
resabs = dabs(resk)
do j=1,3
jtw = j*2
absc = hlgth*xgk(jtw)
fval1 = f(centr-absc) !****************
fval2 = f(centr+absc) !****************
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(dabs(fval1)+dabs(fval2))
enddo
do j = 1,4
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
fval1 = f(centr-absc) !****************
fval2 = f(centr+absc) !****************
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(dabs(fval1)+dabs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(8)*dabs(fc-reskh)
do j=1,7
resasc = resasc+wgk(j)*(dabs(fv1(j)-reskh)+dabs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = dabs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.0d+00) &
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1 &
((epmach*0.5d+02)*resabs,abserr)
count=count+15
return
end subroutine dqk15

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
double precision elist,ermax,errmax,errmin
integer i,ibeg,ido,iord,isucc,j,jbnd,jupbn,k,last,limit,maxerr,&
nrmax,igt,igt1,igt2
dimension elist(last),iord(last)
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer::level,nerr,nmess
character ( len = * ) xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror

——————————————
Key=1の場合, 実軸上3次元の複素函数
（7-15点ガウス求積法）

▼ここクリックでこの場に展開

program main
implicit none
double precision::xa,xb,ya,yb,za,zb,xeps,yeps,zeps
complex(kind(0d0))::s
complex(kind(0d0)),external::f
double precision,parameter::pi=dacos(-1d0)

xa=0d0
xb=pi
ya=0d0
yb=pi
za=0d0
zb=pi
xeps=1d-2
yeps=1d-2
zeps=1d-2
call dqag13(f,xa,xb,ya,yb,za,zb,xeps,yeps,zeps,s)
write(6,*)s

stop
end program main

function f(x,y,z)
implicit none
double precision::x,y,z
complex(kind(0d0))::f

f=(exp(-dcmplx(0d0,1d0)*sqrt(x)*y))*exp(dcmplx(0d0,1d0)*z*z)*sqrt(y)
! f=1d0/(1d0-cos(x)*cos(y)*cos(z))/((2d0*dacos(-1d0))**3)
! f=1d0/(1d0-cos(x))/((2d0*dacos(-1d0))**3)

return
end function f

!===================================

subroutine dqag13(f,a,b,ya,yb,za,zb,eps,yeps,zeps,s)
implicit none
double precision,intent(in)::a,b,eps,ya,yb,yeps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=1
! (Gauss quadrature with 7-15 points)
!
integer::neval,limit,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=10000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0

call dqage13(f,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,ya,yb,yeps,za,zb,zeps)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

write(6,*)count,ier ! Number of times called integrand function

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag13

subroutine dqage13(f,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,ya,yb,yeps,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk153(f,a,b,result,abserr,defabs,resabs,count,ya,yb,yeps,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk153(f,a1,b1,area1,error1,resabs,defab1,count,ya,yb,yeps,za,zb,zeps)
call dqk153(f,a2,b2,area2,error2,resabs,defab2,count,ya,yb,yeps,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage13

subroutine dqk153(f,a,b,result,abserr,resabs,resasc,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,ya,yb,yeps,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(7),fv2(7),wg(4),wgk(8),xgk(8)
data wg ( 1) / 0.129484966168869693270611432679082d0 /
data wg ( 2) / 0.279705391489276667901467771423780d0 /
data wg ( 3) / 0.381830050505118944950369775488975d0 /
data wg ( 4) / 0.417959183673469387755102040816327d0 /
!
data xgk ( 1) / 0.991455371120812639206854697526329d0 /
data xgk ( 2) / 0.949107912342758524526189684047851d0 /
data xgk ( 3) / 0.864864423359769072789712788640926d0 /
data xgk ( 4) / 0.741531185599394439863864773280788d0 /
data xgk ( 5) / 0.586087235467691130294144838258730d0 /
data xgk ( 6) / 0.405845151377397166906606412076961d0 /
data xgk ( 7) / 0.207784955007898467600689403773245d0 /
data xgk ( 8) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.022935322010529224963732008058970d0 /
data wgk ( 2) / 0.063092092629978553290700663189204d0 /
data wgk ( 3) / 0.104790010322250183839876322541518d0 /
data wgk ( 4) / 0.140653259715525918745189590510238d0 /
data wgk ( 5) / 0.169004726639267902826583426598550d0 /
data wgk ( 6) / 0.190350578064785409913256402421014d0 /
data wgk ( 7) / 0.204432940075298892414161999234649d0 /
data wgk ( 8) / 0.209482141084727828012999174891714d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
call dqag1yz(f,centr,ya,yb,yeps,za,zb,zeps,fc,count)
resg = fc*wg(4)
resk = fc*wgk(8)
resabs = abs(resk)

do j=1,3
jtw = j*2
absc = hlgth*xgk(jtw)
call dqag1yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag1yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,4
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
call dqag1yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag1yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(8)*abs(fc-reskh)
do j=1,7
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)

return
end subroutine dqk153

subroutine dqag1yz(f,x,a,b,eps,za,zb,zeps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,a,b,eps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=1
! (Gauss quadrature with 7-15 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=10000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
call dqage1yz(f,x,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,za,zb,zeps)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag1yz

subroutine dqage1yz(f,x,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk15yz(f,x,a,b,result,abserr,defabs,resabs,count,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk15yz(f,x,a1,b1,area1,error1,resabs,defab1,count,za,zb,zeps)
call dqk15yz(f,x,a2,b2,area2,error2,resabs,defab2,count,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage1yz

subroutine dqk15yz(f,x,a,b,result,abserr,resabs,resasc,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(7),fv2(7),wg(4),wgk(8),xgk(8)
data wg ( 1) / 0.129484966168869693270611432679082d0 /
data wg ( 2) / 0.279705391489276667901467771423780d0 /
data wg ( 3) / 0.381830050505118944950369775488975d0 /
data wg ( 4) / 0.417959183673469387755102040816327d0 /
!
data xgk ( 1) / 0.991455371120812639206854697526329d0 /
data xgk ( 2) / 0.949107912342758524526189684047851d0 /
data xgk ( 3) / 0.864864423359769072789712788640926d0 /
data xgk ( 4) / 0.741531185599394439863864773280788d0 /
data xgk ( 5) / 0.586087235467691130294144838258730d0 /
data xgk ( 6) / 0.405845151377397166906606412076961d0 /
data xgk ( 7) / 0.207784955007898467600689403773245d0 /
data xgk ( 8) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.022935322010529224963732008058970d0 /
data wgk ( 2) / 0.063092092629978553290700663189204d0 /
data wgk ( 3) / 0.104790010322250183839876322541518d0 /
data wgk ( 4) / 0.140653259715525918745189590510238d0 /
data wgk ( 5) / 0.169004726639267902826583426598550d0 /
data wgk ( 6) / 0.190350578064785409913256402421014d0 /
data wgk ( 7) / 0.204432940075298892414161999234649d0 /
data wgk ( 8) / 0.209482141084727828012999174891714d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
call dqag1z(f,x,centr,za,zb,zeps,fc,count)
resg = fc*wg(4)
resk = fc*wgk(8)
resabs = abs(resk)

do j=1,3
jtw = j*2
absc = hlgth*xgk(jtw)
call dqag1z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag1z(f,x,centr+absc,za,zb,zeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,4
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
call dqag1z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag1z(f,x,centr+absc,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(8)*abs(fc-reskh)
do j=1,7
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+15
return
end subroutine dqk15yz

subroutine dqag1z(f,x,y,a,b,eps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,y,a,b,eps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=1
! (Gauss quadrature with 7-15 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr

!=============
limit=10000
! limit increase --> converge
!=============

s=dcmplx(0d0,0d0)

allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)

epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0

call dqage1z(f,x,y,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)

lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)

! ier = 0 : success, converged.
! ier > 0 : fail

if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif

deallocate(iwork)
return
end subroutine dqag1z

subroutine dqage1z(f,x,y,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,y
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f

epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk15z(f,x,y,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk15z(f,x,y,a1,b1,area1,error1,resabs,defab1,count)
call dqk15z(f,x,y,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage1z

subroutine dqk15z(f,x,y,a,b,result,abserr,resabs,resasc,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,y
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(7),fv2(7),wg(4),wgk(8),xgk(8)
data wg ( 1) / 0.129484966168869693270611432679082d0 /
data wg ( 2) / 0.279705391489276667901467771423780d0 /
data wg ( 3) / 0.381830050505118944950369775488975d0 /
data wg ( 4) / 0.417959183673469387755102040816327d0 /
!
data xgk ( 1) / 0.991455371120812639206854697526329d0 /
data xgk ( 2) / 0.949107912342758524526189684047851d0 /
data xgk ( 3) / 0.864864423359769072789712788640926d0 /
data xgk ( 4) / 0.741531185599394439863864773280788d0 /
data xgk ( 5) / 0.586087235467691130294144838258730d0 /
data xgk ( 6) / 0.405845151377397166906606412076961d0 /
data xgk ( 7) / 0.207784955007898467600689403773245d0 /
data xgk ( 8) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.022935322010529224963732008058970d0 /
data wgk ( 2) / 0.063092092629978553290700663189204d0 /
data wgk ( 3) / 0.104790010322250183839876322541518d0 /
data wgk ( 4) / 0.140653259715525918745189590510238d0 /
data wgk ( 5) / 0.169004726639267902826583426598550d0 /
data wgk ( 6) / 0.190350578064785409913256402421014d0 /
data wgk ( 7) / 0.204432940075298892414161999234649d0 /
data wgk ( 8) / 0.209482141084727828012999174891714d0 /

epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
fc = f(x,y,centr) ! *************
resg = fc*wg(4)
resk = fc*wgk(8)
resabs = abs(resk)

do j=1,3
jtw = j*2
absc = hlgth*xgk(jtw)
fval1 = f(x,y,centr-absc) ! *************
fval2 = f(x,y,centr+absc) ! *************
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,4
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
fval1 = f(x,y,centr-absc) ! *************
fval2 = f(x,y,centr+absc) ! *************
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(8)*abs(fc-reskh)
do j=1,7
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+15
return
end subroutine dqk15z

subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
double precision elist,ermax,errmax,errmin
integer i,ibeg,ido,iord,isucc,j,jbnd,jupbn,k,last,limit,maxerr,&
nrmax,igt,igt1,igt2
dimension elist(last),iord(last)
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt

subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer::level,nerr,nmess
character ( len = * ) xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror