こちらのページは後程消去いたします。
以下のページに統合しますので、ご参照ください。
https://slpr.sakura.ne.jp/qp/dft-for-numerical-calculation/
本ページにはミスもあり、上の方が正しいですのでご参照ください。
数値計算で離散フーリエ変換を行う方法です。
言語は
fortran90
で
intelのMKL(マス・カーネル・ライブラリー)
を用いて離散フーリエ変換を行いたいと考えます。
高速フーリエ変換は離散フーリエ変換を高速に行う手法のことです。
通常の離散フーリエの計算量のオーダーは、\(O(N^2)\)であり、
基数2の高速フーリエの計算量のオーダーは、\(O(Nlog_2 N)\)です。
基数2は良く言われる通常の配列の個数\(2^m\)個のことを表しています。
離散フーリエ変換を行う際には周期境界条件が課されます。
分点の端で周期境界条件が満たされていない場合、それはその点でステップ関数が含まれることを意味します。
依って予期しない高周波成分が出現するので、注意してください。
一番良い判定方法は関数の対数微分が一致するかどうかを判定するのが良いでしょう。
MKLの離散フーリエ変換ルーチンの概要1
MKLの離散フーリエ変換ルーチンは非常に優秀です。
渡す配列サイズによってプログラムが自動的に判断し、最適な手法で離散フーリエ変換を行います。
MKLのマニュアルによると、
注 : DFT関数は任意の長さをサポートしている。
これらのルーチンは、基数 2 だけでなく、基数 3、5、7、11 に対しても高
性能で広範な機能性を提供する。対応する基数の一覧は、使用しているラ
イブラリー・バージョンの「インテルMKLテクニカル・ユーザー・ノー
ト」を参照のこと。
とあります。
高速フーリエ変換の考え方は\(2^m\)の時だけでなく、\(3^m, 5^m, 7^m, 11^m, \cdots\)の時にも同様に考えることができます。
この時、何の整数乗にするかを区別するために “基数” という言葉を使います。
プログラムを作る場合、通常は一番シンプルな基数”2″が選ばれます。
具体的に配列サイズ\(N\)が
\(N= 2^m\)、ただしmは正の整数(配列をAとするとサイズ\(A(0:2^m-1)\))の時に基数2の高速フーリエ変換が行われます。
それ以外の時は通常の離散フーリエ変換が行われているはずです。
余り自信が無いのではっきりとしたことは言えませんが、分点量(2~20000程度まで)に対するMKLのフーリエ変換の計算速度はほとんどわからないくらいでした。特定の基数の時だけ早いんだろうと予想していましたが、そんなことはなく、それだけ優秀であるという事でしょう。
もう6年前に書かれている記事ですので今はどうなっているかわかりませんが、FFTWと計算速度を比較したページがありましたので載せておきます。
一言でいえば、MKLによる離散フーリエ変換はFFTWよりも早いよ、ということです。
インテル謹製の数値演算ライブラリ「MKL」を使ってプログラムを高速化 3ページ -OSDN, (2009)
MKLの離散フーリエ変換ルーチンの概要2
MKLでの1次元、長さnの順方向離散フーリエ変換は、
\(
\displaystyle z_k=\sum_{j=0}^{n-1}w_je^{-i2\pi jk/n}
\)
に従い行われます(MKLリファレンスマニュアル、11-26)。
数値計算の世界では、余分な係数\(\frac{1}{2\pi}\)をなくすため、指数関数の肩に\(2\pi\)が掛けられたものが良く使用されます。
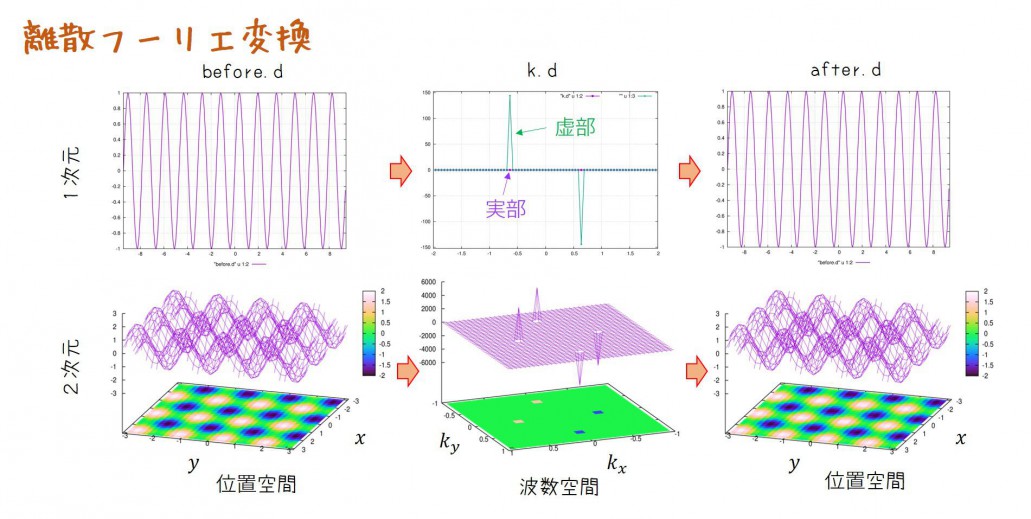
※ここでは、フーリエ変換前の空間を”位置空間“と呼び、フーリエ変換後の空間を”波数空間“と呼ぶことにします。
位置⇔波数ではなく、時間⇔周波数としても同じことなのでどちらでもいいのですが、ここでは、位置⇔波数の呼び方に統一いたします。
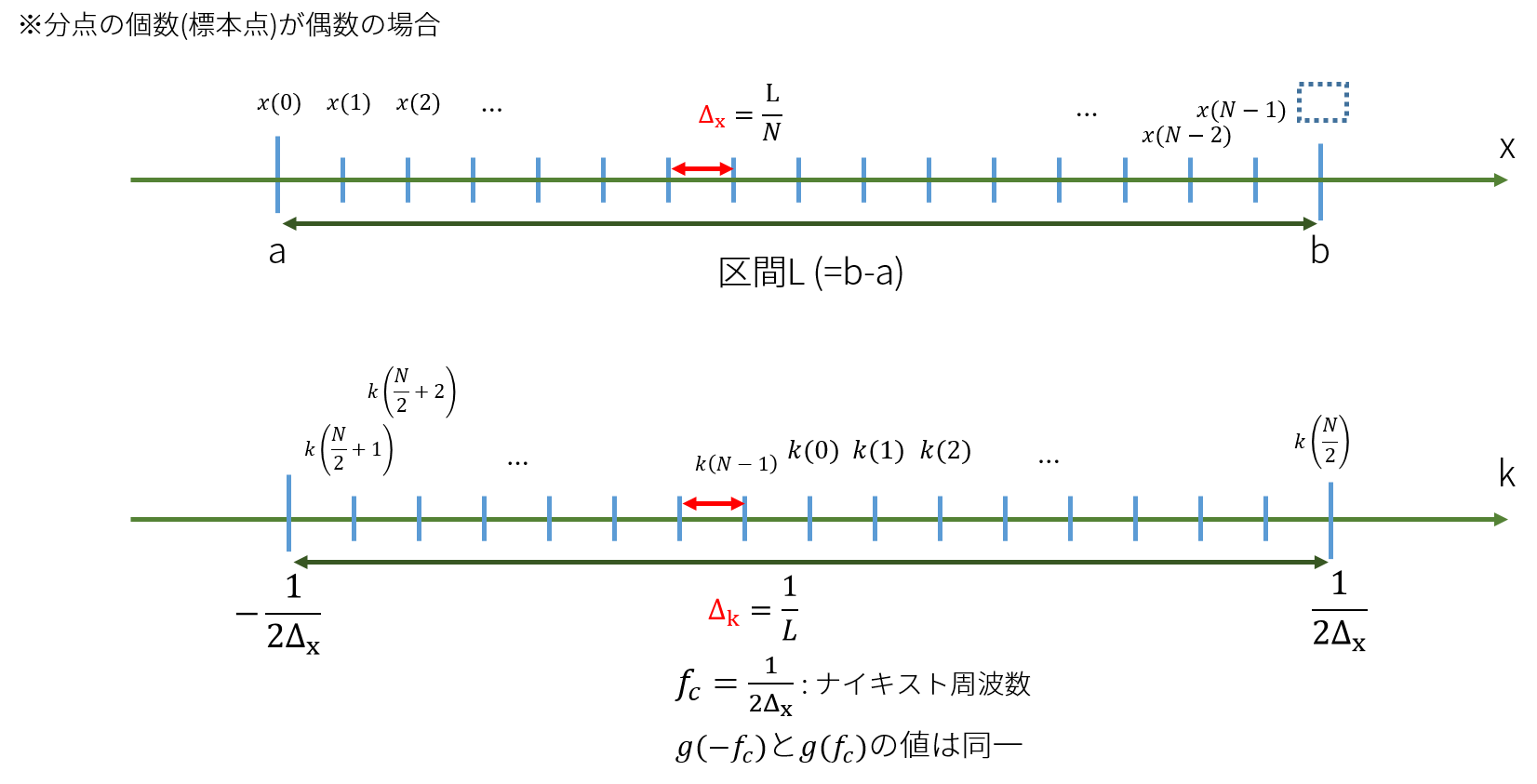
上図のように位置空間上で区間\(L\)の領域で\(N\)個に分割します。
上図はNが偶数の場合です。
MKLの離散フーリエ変換ルーチンはいかなるNに対してもフーリエ変換が可能ですが、奇数の場合、以下のように波数成分の格納が変わります。

\(
f(x)=\sin(\alpha x)
\)
を離散フーリエ変換した場合、
波数空間でのフーリエ変換後のピークは\(k=\frac{\alpha}{2\pi}\)に現れます。
この時、f(x)のフーリエ変換後の関数\(g(k)=F_{[f(x)]}\)は複素数として格納され、上記の場合では
\(
\displaystyle g(k)=i\left\{\frac{N}{2}\delta(k-\frac{\alpha}{2\pi})+\frac{N}{2}\delta(k+\frac{\alpha}{2\pi})\right\}
\)
となります。ここで\(i\)は虚数単位を表し、\(\delta(k)\)はデルタ関数を表します。
波数空間での最大の周波数値\(f_c\)はナイキストの定理より、
\(
\begin{align}
f_c = \frac{1}{2\Delta}, \Delta=\frac{L}{N}
\end{align}
\)
と表されます。これは、波数空間では\(\pm f_c\)までサンプリング可能であることを示しています。
フーリエ変換後の値\(g(k)\)の分点上の和\(S\)、すなわち
\(
\displaystyle S=\sum_{j=0}^{N-1}g(k_j)
\)
は離散フーリエ変換の性質により、\(S\)は分点の総数\(N\)に等しくなります。
逆離散フーリエ変換によって元の空間に戻る場合、規格化因子\(N\)で割らなければなりません。
MKLの1次元離散フーリエ変換ルーチンのプログラム例
使い方はFFT Code Examples -Intel®Developer Zone を参考としました。
例として
関数
\(
f(x)=\sin(4x)
\)
をフーリエ変換し、元に戻すプログラムを書きましょう。
プログラムの流れとしては、
関数\(f(x)\)の位置空間での書き出し(ファイル”before.d”に書き出し、横軸:位置\(x\), 縦軸\(f(x)\))
↓ 順方向フーリエ変換(規格化因子で割られない)
関数\(g(k)=F_{[f(x)]}\)の書き出し(ファイル”k.d”に書き出し、横軸:\(k/(2\pi)\), 縦軸\(g(k)\))
↓ 逆方向フーリエ変換(規格化因子Nで割られる)
関数\(f(x)=F^{-1}_{[g(k)]}\)の書き出し(ファイル”after.d”に書き出し、横軸:x, 縦軸f(x))
になっています。
コンパイルを行うにあたり重要な事が2点あります。
1, MKLを使う事
2, fftサブルーチンの上にinclude文を付け加える事(かも?)
このincludeは、MKLにある離散フーリエ変換ルーチンを使いますよーというサインであり、パスはMKLのバージョンや、インストールした状況によって変わります。
うまく、ファイル”mkl_dfti.f90″を見つけてください。パスを上から辿っていくのがいいと思います。
※2016/02/27時点での最新バージョン(ifort –version で確認できます)
ifort (IFORT) 16.0.2 20160204
において、mkl_dfti.fのデフォルトでの場所は、
“/opt/intel/compilers_and_libraries_2016/linux/mkl/include/mkl_dfti.f90”
です。また、このバージョンだけかどうかわかりませんが、include文が無くてもどうやら動くようです。
プログラムのコンパイルと実行は
$ ifort -mkl main.f90
$ ./a.out
で良いでしょう。
サブルーチンのコンセプトは、
ただ順/逆方向離散フーリエ変換をしてくれるサブルーチンです。速度は追求していません。
速度を追及する書き方をしているのは下のベンチマークの項目です。プログラムの可読性が悪くなるので、中身を知らないと調整が出来ません。
ベンチマークに書いてあるように、サブルーチンdftの中身の
Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,n)
Status = DftiCommitDescriptor(hand)
Status = DftiFreeDescriptor(hand)
はFFTを使うための準備で、これは配列の大きさが変わらない限り1度実行するだけで良いのです。
これを排除すると3-4倍ほど速くなります。
include "/opt/intel/mkl/include/mkl_dfti.f90"
program main
implicit none
integer::i,n
double precision,allocatable::x(:),k(:),mk(:)
complex(kind(0d0)),allocatable::z(:),mz(:)
double precision::hx,xmin,xmax
double precision,parameter::pi=dacos(-1.d0)
complex(kind(0d0))::func
external::func
n=130
allocate(x(0:n-1),k(0:n-1),z(0:n-1))
x=0d0; k=0d0; z=dcmplx(0d0,0d0)
allocate(mk(0:n-1),mz(0:n-1))
mk=0d0; mz=dcmplx(0d0,0d0)
xmin=-3d0*pi
xmax=3d0*pi
hx=(xmax-xmin)/dble(n)
do i=0,n-1
x(i)=xmin+dble(i)*hx
z(i)=func(x(i))
enddo
open(21,file="before.d")
do i=0,n-1
write(21,'(3e20.10e3)')x(i),dble(z(i)),dimag(z(i))
enddo
close(21)
call dftf(n,k,hx) ! Get frequency k
call dft(n,z,"forward") ! forward dft
call dfts(n,k,z,mk,mz) !sort frequency
open(21,file="k.d")
do i=0,n-1
write(21,'(3e20.10e3)')mk(i),dble(mz(i)),dimag(mz(i))
enddo
close(21)
call dft(n,z,"backward") ! backward dft
open(21,file="after.d")
do i=0,n-1
write(21,'(3e20.10e3)')x(i),dble(z(i)),dimag(z(i))
enddo
close(21)
stop
end program main
function func(x)
implicit none
double precision::x
complex(kind(0d0))::func
func=dcmplx(dsin(4d0*x),0d0)
return
end function func
!-------------------------------
subroutine dft(n,z,FB)
!sikinote
! developer : sikino
! date : 2015/09/20
use MKL_DFTI
implicit none
integer,intent(in)::n
complex(kind(0d0)),intent(inout)::z(0:n-1)
character(*)::FB
integer::Status
TYPE(DFTI_DESCRIPTOR),POINTER::hand
!DFT : Discrete Fourier Transform
!
!n --> number of data.
!z(i) --> value of data at x(i)
!FB --> "forward" : Forward DFT
! --> "backward" : Backward DFT
Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,n)
Status = DftiCommitDescriptor(hand)
if(trim(FB).eq."forward")then
Status = DftiComputeForward(hand,z)
elseif(trim(FB).eq."backward")then
Status = DftiComputeBackward(hand,z)
else
write(6,*)"DFT string different"
stop
endif
Status = DftiFreeDescriptor(hand)
if(trim(FB).eq."backward")then
z=z/dble(n)
end if
return
end subroutine dft
subroutine dfts(N,f,z,mf,mz)
!sikinote
! developer : sikino
! date : 2015/09/20
implicit none
integer,intent(in)::N
double precision,intent(in)::f(0:N-1)
double precision,intent(out)::mf(0:N-1)
complex(kind(0d0)),intent(in)::z(0:N-1)
complex(kind(0d0)),intent(out)::mz(0:N-1)
integer::i,j
if(mod(n,2).eq.0)then
do i=0,N-1
if(i.le.N/2)then
j=i+N/2-1
mf(j)=f(i)
mz(j)=z(i)
else
j=i-N/2-1
mf(j)=f(i)
mz(j)=z(i)
endif
enddo
else
do i=0,N-1
if(i.le.(N-1)/2)then
j=i+(N-1)/2
mf(j)=f(i)
mz(j)=z(i)
else
j=i-(N-1)/2-1
mf(j)=f(i)
mz(j)=z(i)
endif
enddo
endif
return
end subroutine dfts
subroutine dftf(N,f,h)
!sikinote
! developer : sikino
! date : 2015/09/20
implicit none
integer,intent(in)::N
double precision,intent(in)::h
double precision,intent(out)::f(0:N-1)
integer::i
double precision::mf(0:N-1)
if(mod(N,2).eq.0)then
do i=0,N-1
mf(i)=(dble(i+1)-dble(N)*0.5d0)/(dble(N)*h)
enddo
do i=0,N-1
if(i.le.N/2-2)then
f(i+N/2+1)=mf(i)
else
f(i-N/2+1)=mf(i)
endif
enddo
else
do i=0,N-1
mf(i)=(dble(i)-dble(N-1)*0.5d0)/(dble(N)*h)
enddo
do i=0,N-1
if(i.le.(N-1)/2-1)then
f(i+(N-1)/2+1)=mf(i)
else
f(i-(N-1)/2)=mf(i)
endif
enddo
endif
return
end subroutine dftf
上で用いているサブルーチン
dft,dfts,dftfはそれぞれフーリエ変換、フーリエ変換後の空間の値、ソート用のルーチンであることを意味し、その中身は以下のようなものです。例のごとく、MKLのルーチンはそのままでは使いにくいので1クッション挟みます。
ここ↑に書いてあるサブルーチン
- dft(N,z,FB)
- dftf(N,f,h)
- dfts(N,f,z,mf,mz)
を説明します。
-
dft(N,z,FB)
このルーチンによって順/逆方向フーリエ変換が行われます。
引数はそれぞれ
- (入力) N : integer, データ配列のサイズ
- (入出力) z : complex(kind(0d0)), データ配列z(0:N-1)
- (入力) FB : character, 順方向(“forward”)、逆方向(“backward”)の指定
です。データ配列に上書きして値が返ってきます。
サイズNのデータ配列z,順方向の離散フーリエ変換をしたい場合は、
call dft(size(z,1),z,"forward")
とするのがいいでしょう。
規格化は順方向の時には行わず、逆方向の時にだけ\(1/N\)を掛けています。
-
dftf(N,f,h)
このルーチンは波数空間での横軸の値f(0:N-1)を与えます。
引数はそれぞれ
- (入力) N : integer, データ配列のサイズ
- (出力) f : double precision, 波数空間の横軸の値f(0:N-1)
- (入力) h : double precision, 位置空間でのサンプルレート(刻み幅)
です。
波数fの順番は少しややこしく、

となっています。
また、ここで出力されるfは波数を\(2\pi\)で割ったものが出力されます。
具体的には、\(\sin(x)\)をMKLのフーリエ変換を行いグラフを書くとフーリエ変換後の空間(波数空間)で、ピークの位置は\(\pm 0.159115494309\cdots (\sim \frac{1}{2\pi})\)に表れることを意味します。
また、変換先の空間をグラフで描画したい時に値を小さい順に並べ替えたい必要が出てきたときは並べ替え用のルーチンdftsを使用してください。
-
dfts(N,f,z,mf,mz)
このルーチンは変換先の波数空間でグラフを描画したい時に、順番を値を小さい順に並べ替えます。
引数はそれぞれ
- (入力) N : integer, データ配列のサイズ
- (入力) f : double precision, 波数空間の横軸の値f(0:N-1)
- (入力) z : complex(kind(0d0)), 波数空間でのデータ配列z(0:N-1)
- (出力) mf : double precision, 並び替えられた波数空間の横軸の値mf(0:N-1)
- (出力) mz : complex(kind(0d0)), 並び替えられた波数空間でのデータ配列z(0:N-1)
です。上書きして引数を返す必要性がないだろう、と判断して別の配列に書き出させています。
もしもメモリが足らないとか、気に食わない人は書き換えてください。
[adsense1]
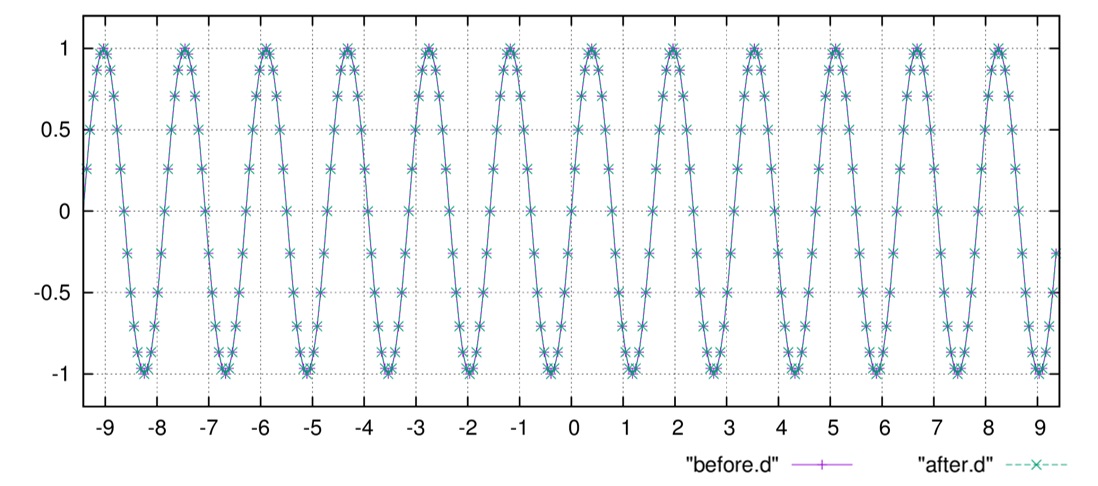
出力ファイル”before.d”, “k.d”, “after.d”を書いてみます。
位置空間での区間\([-3\pi\sim3\pi]\)で、分点数\(N=288\)で行った場合、
位置空間での波形、この場合は\(\sin(4x)\)が描かれます。
波数空間では
\(
\displaystyle g(k)=i\left\{\frac{288}{2}\delta(k-\frac{4}{2\pi})+\frac{288}{2}\delta(k+\frac{4}{2\pi})\right\}
\)
が得られるはずで、実際にプロットして確かめてみると
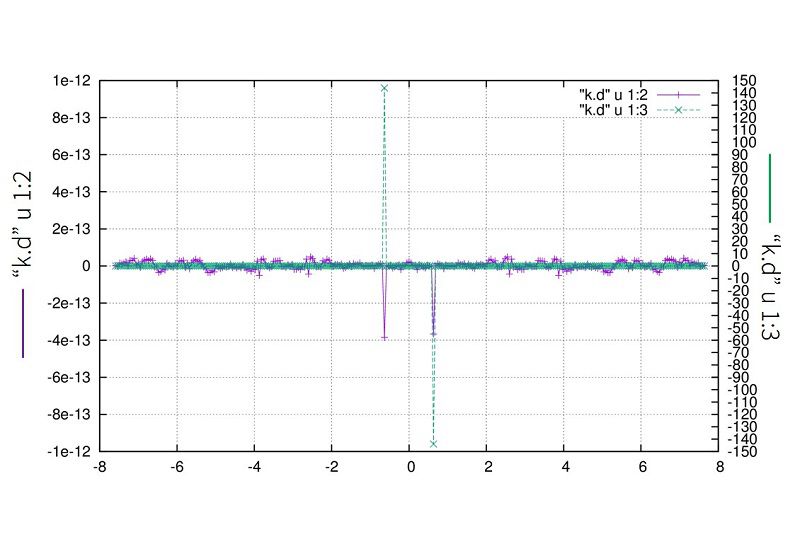
となります。
※Nは2以上のどんな整数でもokです。偶数、奇数、素数であっても。
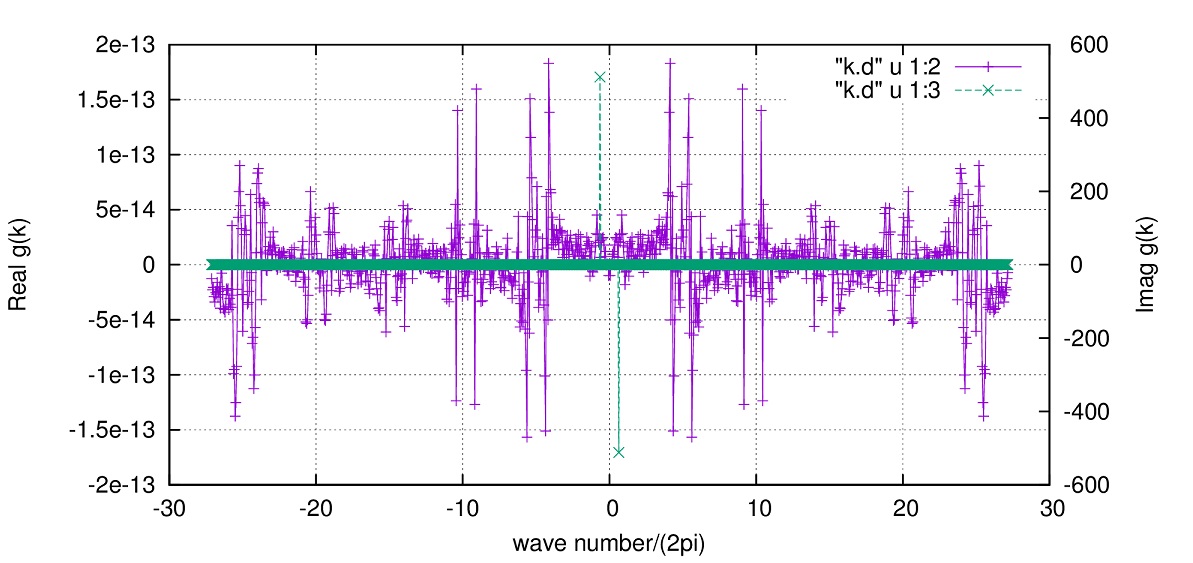
※実部に現れる小さなピークに関して
原因はよくわかりません。\(N=2^m\)ではない時になんかこれが出てきます。
不安な人は\(N=2^m\)に固定して使ってください。
N=1024で行うとこうなります。
ベンチマーク
同じ計算機上でのベンチマーク結果を載せます。
コンパイラ:ifort (IFORT) 16.0.2 20160204
MKL:/opt/intel/compilers_and_libraries_2016.2.181
計算スレッド数1
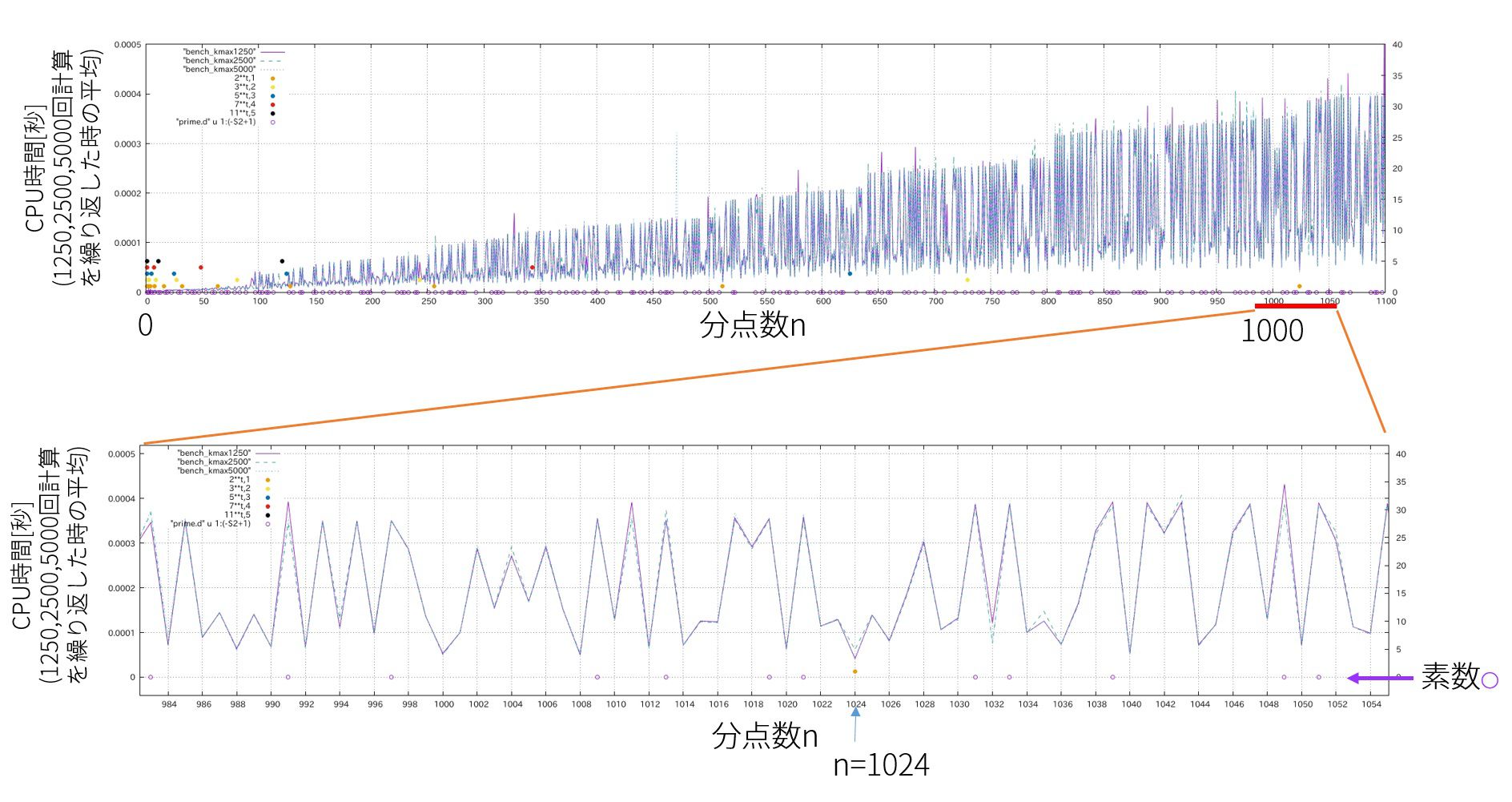
ベンチマーク用プログラムはこちら↓
program main
implicit none
integer::i,n
double precision,allocatable::x(:)
complex(kind(0d0)),allocatable::z(:)
double precision::hx,xmin,xmax
double precision,parameter::pi=dacos(-1.d0)
complex(kind(0d0))::func
external::func
call mkl_set_num_threads(1)
do n=2,1100
if(mod(n,50).eq.0)write(6,*)”n –> “,n
allocate(x(0:n-1),z(0:n-1))
z=dcmplx(0d0,0d0)
xmin=-3d0*pi
xmax=3d0*pi
hx=(xmax-xmin)/dble(n)
do i=0,n-1
x(i)=xmin+dble(i)*hx
z(i)=func(x(i))
enddo
call benchm(n,z)
deallocate(x,z)
enddo
stop
end program main
function func(x)
implicit none
double precision::x
complex(kind(0d0))::func
func=dcmplx(dsin(4d0*x),0d0)
return
end function func
subroutine benchm(n,z)
implicit none
integer::n,k,kmax
double precision::t0,t1
complex(kind(0d0))::z(0:n-1)
kmax=1250
call cpu_time(t0)
do k=1,kmax
call dft(n,z,”forward”) ! forward dft
call dft(n,z,”backward”) ! backward dft
enddo
call cpu_time(t1)
write(10,'(i5,e20.10e4,A)’)n,(t1-t0)/dble(kmax)
return
end subroutine benchm
subroutine dft(n,z,FB)
!sikinote
! developer : sikino
! date : 2015/09/20
use MKL_DFTI
implicit none
integer,intent(in)::n
complex(kind(0d0)),intent(inout)::z(0:n-1)
character(*)::FB
integer::Status
TYPE(DFTI_DESCRIPTOR),POINTER::hand
!DFT : Discrete Fourier Transform
!
!n –> number of data.
!z(i) –> value of data at x(i)
!FB –> “forward” : Forward DFT
! –> “backward” : Backward DFT
Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,n)
Status = DftiCommitDescriptor(hand)
if(trim(FB).eq.”forward”)then
Status = DftiComputeForward(hand,z)
elseif(trim(FB).eq.”backward”)then
Status = DftiComputeBackward(hand,z)
else
write(6,*)”DFT string different”
stop
endif
Status = DftiFreeDescriptor(hand)
if(trim(FB).eq.”backward”)then
z=z/dble(n)
end if
return
end subroutine dft
subroutine dfts(N,f,z,mf,mz)
!sikinote
! developer : sikino
! date : 2015/09/20
implicit none
integer,intent(in)::N
double precision,intent(in)::f(0:N-1)
double precision,intent(out)::mf(0:N-1)
complex(kind(0d0)),intent(in)::z(0:N-1)
complex(kind(0d0)),intent(out)::mz(0:N-1)
integer::i,j
if(mod(n,2).eq.0)then
do i=0,N-1
if(i.le.N/2)then
j=i+N/2-1
mf(j)=f(i)
mz(j)=z(i)
else
j=i-N/2-1
mf(j)=f(i)
mz(j)=z(i)
endif
enddo
else
do i=0,N-1
if(i.le.(N-1)/2)then
j=i+(N-1)/2
mf(j)=f(i)
mz(j)=z(i)
else
j=i-(N-1)/2-1
mf(j)=f(i)
mz(j)=z(i)
endif
enddo
endif
return
end subroutine dfts
subroutine dftf(N,f,h)
!sikinote
! developer : sikino
! date : 2015/09/20
implicit none
integer,intent(in)::N
double precision,intent(in)::h
double precision,intent(out)::f(0:N-1)
integer::i
double precision::mf(0:N-1)
if(mod(N,2).eq.0)then
do i=0,N-1
mf(i)=(dble(i+1)-dble(N)*0.5d0)/(dble(N)*h)
enddo
do i=0,N-1
if(i.le.N/2-2)then
f(i+N/2+1)=mf(i)
else
f(i-N/2+1)=mf(i)
endif
enddo
else
do i=0,N-1
mf(i)=(dble(i)-dble(N-1)*0.5d0)/(dble(N)*h)
enddo
do i=0,N-1
if(i.le.(N-1)/2-1)then
f(i+(N-1)/2+1)=mf(i)
else
f(i-(N-1)/2)=mf(i)
endif
enddo
endif
return
end subroutine dftf
並列計算時の計算速度
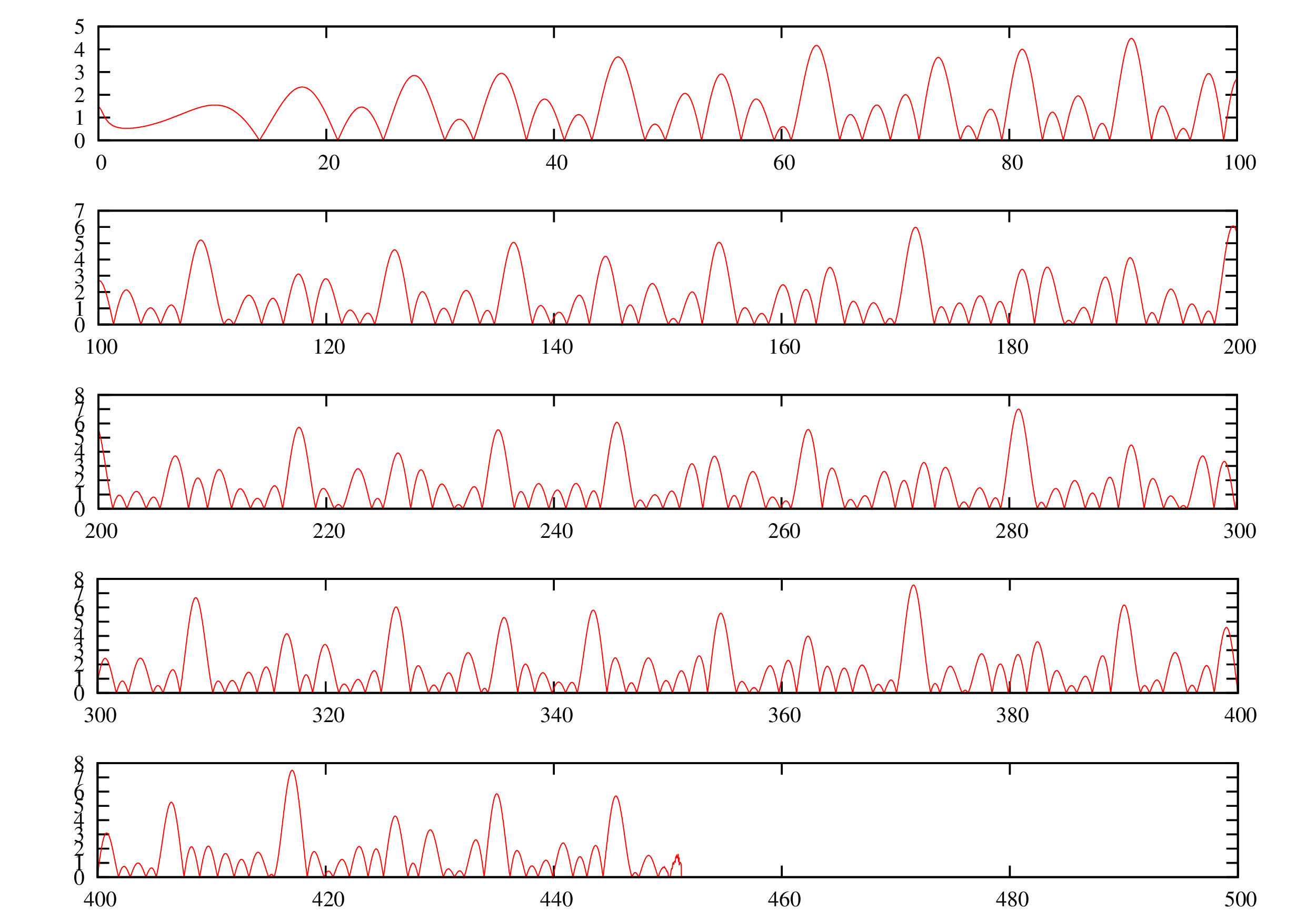
call mkl_set_num_threads(Ncpu)
を用いてFFTを並列計算で行った時、計算時間のCPU個数(8コア16スレッド)と配列の要素数依存性を調べます。
フーリエ変換するのはガウス関数とします。
結果はこのようになりました。
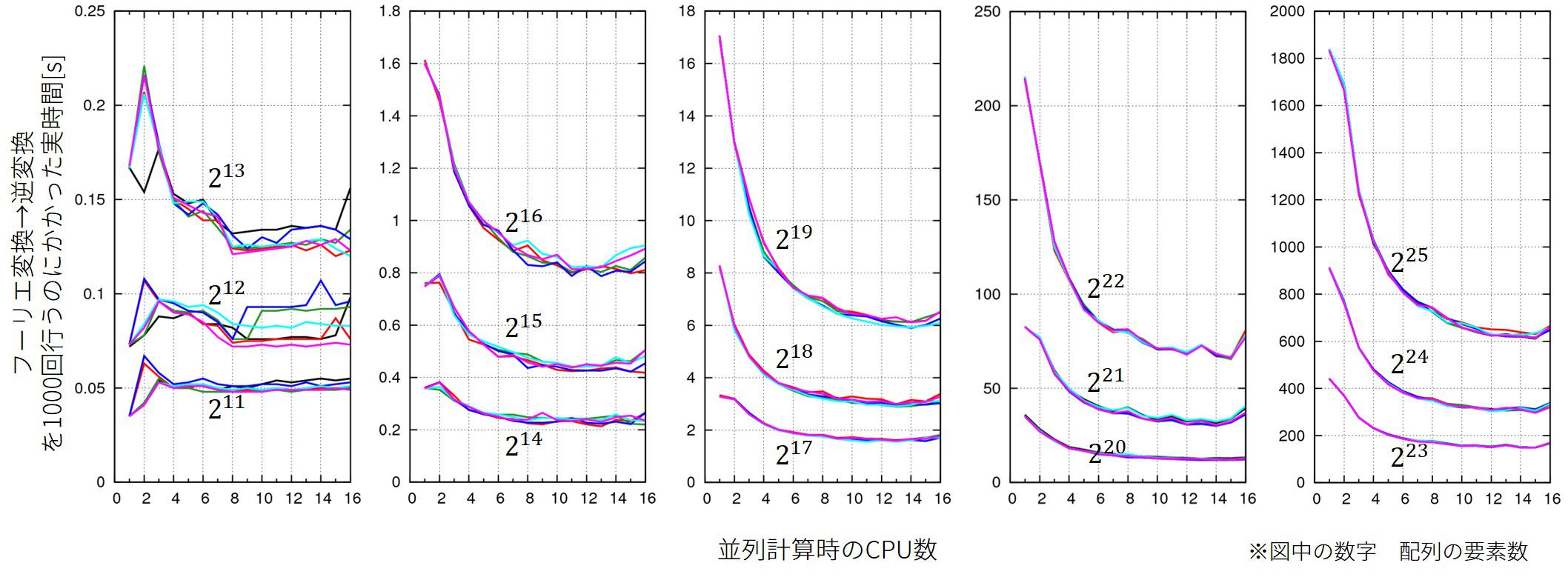
複数の線は試行回数を表しています。プログラムは全く同じで、実行した時刻だけが違います。
”計算1回”とは(順方向→逆方向フーリエ変換)の1セットを”1回”としています。
8コア16スレッドの環境で実行したので、物理的なCPUの個数8個で計算速度はおおよそ打ち止めになっています。
計算に用いたコードはこちら
program main
implicit none
integer::i,n,j,Nr,l,Ntry,jx
double precision,allocatable::x(:),k(:),mk(:)
complex(kind(0d0)),allocatable::z(:),mz(:)
double precision::hx,xmin,xmax
character(48)::fname
integer::ti,tf,tr
double precision,parameter::pi=dacos(-1.d0)
complex(kind(0d0))::func
external::func
xmin=-3d0*pi
xmax=3d0*pi
Ntry=10
do l=1,Ntry
write(fname,'(A,i0,A)')"ffttime_",l,".d"
open(11,file=trim(fname))
do jx=5,25
n=2**jx
allocate(x(0:n-1),k(0:n-1),z(0:n-1))
x=0d0; k=0d0; z=dcmplx(0d0,0d0)
hx=(xmax-xmin)/dble(n)
do i=0,n-1
x(i)=xmin+dble(i)*hx
z(i)=func(x(i))
enddo
Nr=1000
do j=1,16
call mkl_set_num_threads(j)
call system_clock(ti)
call fft(n,z,0,Nr)
call system_clock(tf,tr)
write(11,'(i6,i8,f10.3,2i6)')j,jx,(tf-ti)/dble(tr),Nr
write(6,'(i6,i8,f10.3,2i6)')j,jx,(tf-ti)/dble(tr),Nr
enddo
write(11,*)
deallocate(x,k,z)
enddo
close(11)
enddo
stop
end program main
function func(x)
implicit none
double precision::x
complex(kind(0d0))::func
func=exp(-0.5d0*x*x)
return
end function func
include "/opt/intel/mkl/include/mkl_dfti.f90"
subroutine fft(N,z,ifb,Ncycle)
use MKL_DFTI
implicit none
integer,intent(in)::N,ifb,Ncycle
complex(kind(0d0)),intent(inout)::z(0:N-1)
integer::Status,i
TYPE(DFTI_DESCRIPTOR),POINTER::hand
Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,N)
Status = DftiCommitDescriptor(hand)
!if(ifb.eq.1)Status = DftiComputeForward(hand,z)
!if(ifb.eq.-1)Status = DftiComputeBackward(hand,z)
do i=1,Ncycle
Status = DftiComputeForward(hand,z)
Status = DftiComputeBackward(hand,z)
z=z/n
enddo
Status = DftiFreeDescriptor(hand)
return
end subroutine fft
2次元のフーリエ変換について
ルーチン等々はほぼ同じです。
下のプログラムは
\(
f(x,y)=\sin(4x)+\sin(3y)
\)
をフーリエ変換するものです。
フーリエ変換実行前の,位置空間での関数の形(“before.d”, x軸:\(x\), y軸:\(y\), z軸\(f(x,y)\)),
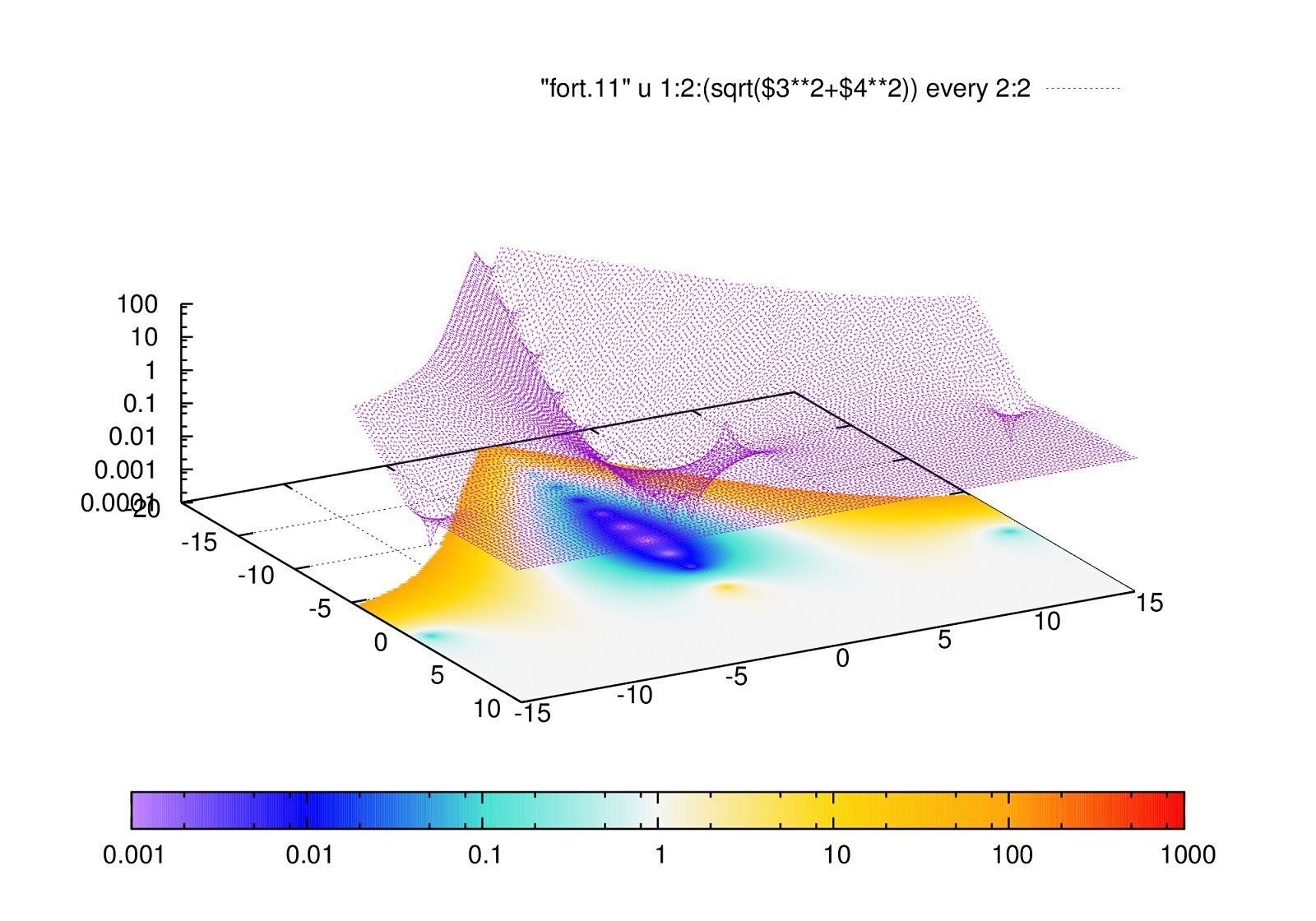
フーリエ変換し、波数空間で見た関数の形(“k.d”, x軸:\(k_x/(2\pi)\), y軸:\(k_y/(2\pi)\), z軸\(Imag\{g(k_x,k_y)\}\)),
逆フーリエ変換した後の関数の形(“after.d”, x軸:\(x\), y軸:\(y\), z軸\(f(x,y)\))は
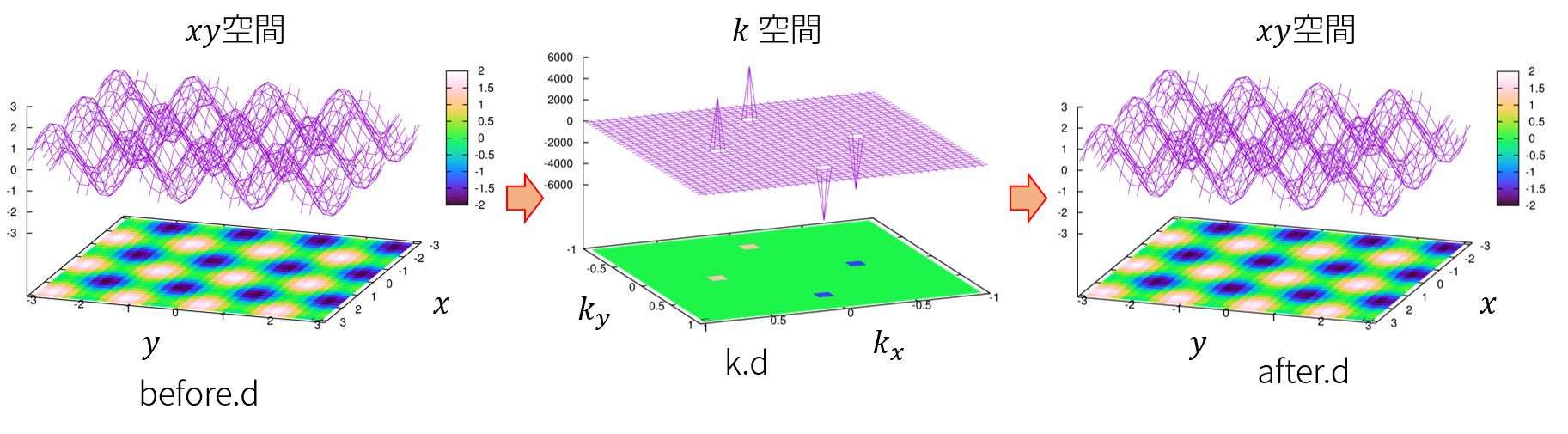
となります。
波数空間で\(k_x\)だけを見た時,\(k_x=0\)にあたかもピークが見えます。
これはy成分があるために出てくるもので、証明は以下のようにできます。
関数\(f(x,y)\)は
\(
\begin{align}
f(x,y)&=\sin(4x)+\sin(3y)\\
&=i\left\{-\frac{1}{2}e^{i4x}+\frac{1}{2}e^{-i4x}-\frac{1}{2}e^{i3y}+\frac{1}{2}e^{-i3y}\right\}
\end{align}
\)
なので、連続のフーリエ変換を考えるとすると、
\(
\begin{align}
&\int f(x,y)e^{-ik_x x}e^{-ik_y y}dxdy\\
&=i\left\{-\frac{1}{2}\int e^{i(4-k_x)x} dx \int e^{-ik_y y} dy+\frac{1}{2}\int e^{-i(4+k_x)x} dx \int e^{-ik_y y} dy \right. \\
&\;\;\;\;\;\;\;\;\;\;\;\; \left.-\frac{1}{2}\int e^{-ik_x x} dx \int e^{i(3-k_y)y} dy+\frac{1}{2}\int e^{-ik_x x} dx \int e^{-i(3+k_y)y} dy\right\} \\
&=i\pi\left\{-\delta(k_x-4)\delta(k_y)+\delta(k_x+4)\delta(k_y)-\delta(k_x)\delta(k_y-3)+\delta(k_x)\delta(k_y+3)\right\}
\end{align}
\)
となります。なので、フーリエ変換によってピークが出てくる位置というのは、
\((k_x,k_y)=(4,0), (-4,0), (0,3), (0,-3)\)
の4点となります。なので、y成分がいるために\(k_x=0\)にあたかもピークがあるように見えてしまうんですね。(証明終わり)
2次元のフーリエ変換はそのまま2次元データの配列を渡すことは出来ないため、一度、1次元配列への変換(サブルーチンswap1d2d)を呼び出しています。本来は2次元データと1次元データの間の関係ではEquivalenceを使うべきなのですが、何をしているのかの(個人的な)見やすさを考慮してわざわざ別の配列を用意して格納しています。
include "/opt/intel/mkl/include/mkl_dfti.f90"
program main
implicit none
integer::i,j,Nx,Ny
double precision,allocatable::x(:),kx(:),mkx(:)
double precision,allocatable::y(:),ky(:),mky(:)
double precision::hx,xmin,xmax
double precision::hy,ymin,ymax
complex(kind(0d0)),allocatable::z(:,:),mz(:,:)
double precision,parameter::pi=dacos(-1.d0)
complex(kind(0d0))::func
external::func
Nx=100; Ny=100
allocate(x(0:Nx-1),kx(0:Nx-1),mkx(0:Nx-1))
x=0d0; kx=0d0; mkx=0d0
allocate(y(0:Ny-1),ky(0:Ny-1),mky(0:Ny-1))
y=0d0; ky=0d0; mky=0d0
allocate(z(0:Nx-1,0:Ny-1),mz(0:Nx-1,0:Ny-1))
z=dcmplx(0d0,0d0); mz=dcmplx(0d0,0d0)
xmin=-3d0<em>pi
xmax=3d0</em>pi
hx=(xmax-xmin)/dble(Nx)
ymin=-3d0<em>pi
ymax=3d0</em>pi
hy=(ymax-ymin)/dble(Ny)
do i=0,Nx-1
x(i)=xmin+dble(i)<em>hx
enddo
do j=0,Ny-1
y(j)=ymin+dble(j)</em>hy
enddo
do i=0,Nx-1
do j=0,Ny-1
z(i,j)=func(x(i),y(j))<br />
enddo
enddo
open(21,file="before.d")
do i=0,Nx-1
do j=0,Ny-1
write(21,'(4e20.10e3)')x(i),y(j),dble(z(i,j)),dimag(z(i,j))
enddo
write(21,*)
enddo
close(21)
call dftf(Nx,kx,hx); call dftf(Ny,ky,hy) ! get frequency
call dft2d(Nx,Ny,z,"forward") ! forward dft
call dfts2d(Nx,Ny,kx,ky,z,mkx,mky,mz) !sort frequency
open(21,file="k.d")
do i=0,Nx-1
do j=0,Ny-1
write(21,'(4e20.10e3)')mkx(i),mky(j),dble(mz(i,j)),dimag(mz(i,j))
enddo
write(21,*)
enddo
close(21)
call dft2d(Nx,Ny,z,"backward") ! backward dft
open(21,file="after.d")
do i=0,Nx-1
do j=0,Ny-1
write(21,'(4e20.10e3)')x(i),y(j),dble(z(i,j)),dimag(z(i,j))
enddo
write(21,*)
enddo
close(21)
stop
end program main
function func(x,y)
implicit none
double precision::x,y
complex(kind(0d0))::func
func=dcmplx(dsin(4d0<em>y)+dsin(3d0</em>x),0d0)
return
end function func
がメインのプログラムで、以下が上で呼び出しているサブルーチンの中身です。
subroutine dftf(N,f,h)
implicit none
integer,intent(in)::N
double precision,intent(in)::h
double precision,intent(out)::f(0:N-1)
integer::i
double precision::mf(0:N-1)
if(mod(N,2).eq.0)then
do i=0,N-1
mf(i)=(dble(i+1)-dble(N)<em>0.5d0)/(dble(N)</em>h)
enddo
<pre><code> do i=0,N-1
if(i.le.N/2-2)then
f(i+N/2+1)=mf(i)
else
f(i-N/2+1)=mf(i)
endif
enddo
else
do i=0,N-1
mf(i)=(dble(i)-dble(N-1)0.5d0)/(dble(N)h)
enddo
do i=0,N-1
if(i.le.(N-1)/2-1)then
f(i+(N-1)/2+1)=mf(i)
else
f(i-(N-1)/2)=mf(i)
endif
enddo
endif
return
end subroutine dftf
!——————————–
subroutine dft2d(Nx,Ny,z,FB)
!sikinote
!date : 2015/12/29
!developer : sikino
!CC BY 4.0 (http://creativecommons.org/licenses/by/4.0/deed.ja)
use MKL_DFTI
implicit none
integer,intent(in)::Nx,Ny
complex(kind(0d0)),intent(inout)::z(0:Nx-1,0:Ny-1)
character(*),intent(in)::FB
complex(kind(0d0))::z1(0:Nx*Ny-1)
integer::Status
TYPE(DFTI_DESCRIPTOR),POINTER::hand
integer::id(1:2)
!DFT : Discrete Fourier Transform
!
!n –> number of data.
!z(i,j) –> value of data at x and y
!FB –> “forward” : Forward DFT
! –> “backward” : Backward DFT
call swap1d2d(nx,ny,z,z1,1)
id(1)=nx; id(2)=ny
Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,2,id)
Status = DftiCommitDescriptor(hand)
if(trim(FB).eq.”forward”)then
Status = DftiComputeForward(hand,z1)
elseif(trim(FB).eq.”backward”)then
Status = DftiComputeBackward(hand,z1)
else
write(6,*)”DFT string different”
stop
endif
Status = DftiFreeDescriptor(hand)
call swap1d2d(nx,ny,z,z1,-1)
if(trim(FB).eq.”backward”)then
z=z/dble(nx*ny)
end if
return
end subroutine dft2d
!———————————————
subroutine swap1d2d(nx,ny,z2,z1,isign)
!change array matrix between 1D and 2D
! if isign == 1 –> from 2D to 1D
! if isign == -1 –> from 1D to 2D
implicit none
integer,intent(in)::nx,ny,isign
complex(kind(0d0)),dimension(0:nx-1,0:ny-1),intent(inout)::z2
complex(kind(0d0)),dimension(0:nx*ny-1),intent(inout)::z1
integer::j1,j2,k
if(isign.eq.1)then
do j2=0,ny-1
do j1=0,nx-1
k=j2nx+j1
z1(k)=z2(j1,j2)
enddo
enddo
elseif(isign.eq.-1)then
do j2=0,ny-1
do j1=0,nx-1
k=j2nx+j1
z2(j1,j2)=z1(k)
enddo
enddo
endif
return
end subroutine swap1d2d
!—————————-
subroutine dfts2d(Nx,Ny,fx,fy,z,mfx,mfy,mz)
implicit none
integer,intent(in)::Nx,Ny
double precision,intent(in)::fx(0:Nx-1),fy(0:Ny-1)
complex(kind(0d0))::z(0:Nx-1,0:Ny-1)
double precision,intent(out)::mfx(0:Nx-1),mfy(0:Ny-1)
complex(kind(0d0)),intent(out)::mz(0:Nx-1,0:Ny-1)
complex(kind(0d0))::mmz(0:Nx-1,0:Ny-1)
integer::i,j,k,l
if(mod(Ny,2).eq.0)then
do i=0,Ny-1
if(i.le.Ny/2)then
j=i+Ny/2-1
mfy(j)=fy(i)
mz(0:Nx-1,j)=z(0:Nx-1,i)
else
j=i-Ny/2-1
mfy(j)=fy(i)
mz(0:Nx-1,j)=z(0:Nx-1,i)
endif
enddo
else
do i=0,Ny-1
if(i.le.(Ny-1)/2)then
j=i+(Ny-1)/2
mfy(j)=fy(i)
mz(0:Nx-1,j)=z(0:Nx-1,i)
else
j=i-(Ny-1)/2-1
mfy(j)=fy(i)
mz(0:Nx-1,j)=z(0:Nx-1,i)
endif
enddo
endif
mmz=mz
if(mod(Nx,2).eq.0)then
do k=0,Nx-1
if(k.le.Nx/2)then
l=k+Nx/2-1
mfx(l)=fx(k)
mz(l,0:Ny-1)=mmz(k,0:Ny-1)
else
l=k-Nx/2-1
mfx(l)=fx(k)
mz(l,0:Ny-1)=mmz(k,0:Ny-1)
endif
enddo
else
do k=0,Nx-1
if(k.le.(Nx-1)/2)then
l=k+(Nx-1)/2
mfx(l)=fx(k)
mz(l,0:Ny-1)=mmz(k,0:Ny-1)
else
l=k-(Nx-1)/2-1
mfx(l)=fx(k)
mz(l,0:Ny-1)=mmz(k,0:Ny-1)
endif
enddo
endif
return
end subroutine dfts2d
昔のMKLの離散フーリエ変換ルーチンについて
MKLは汎用性を高くするために仕様変更が行われ、
以前は
とするだけで順/逆方向フーリエ変換は使えていたようですが、いつからか(2004~2006年辺り?)廃止され、使えなくなっています。
間違い、勘違いがあると思います。
いかなる問題が発生しても私は責任を一切負いません。
それを念頭に置いたうえ使用してください。
参考文献
インテル®マス・カーネル・ライブラリーリファレンスマニュアル(2006年)
ニューメリカルレシピinC
[adsense2]