【重要なお知らせ】
いつもシキノートをご覧いただき、誠にありがとうございます。
7年近くに渡り本ページを更新してきましたが、さまざまな事情により本ページの更新を停止し、別のページに移行することにいたしました。
これまでのご支援、ご理解、そして何よりも貴重なご意見やフィードバックをいただいたこと、深く感謝いたします。
新しいウェブサイトは、下記リンク先になります。
https://slpr.sakura.ne.jp/sikinote/
今後とも、ご指導ご鞭撻のほど、宜しくお願い申し上げます。
sikino のすべての投稿
一般固有値問題の対角化のプログラム（実対称行列、Fortran90）
intel Math Karnel Library (以降MKL)を用いて、一般固有値問題の対角化を行います。
特に、登場する行列が実対称行列である場合について考えます。
PDF版はこちらをどうぞ。
https://slpr.sakura.ne.jp/qp/supplement_data/diagonalize/GeneralizedEVP_symmetrixMatrix.pdf
概要
本稿で取り扱う一般固有値問題は、下記の固有値問題です。
\(\displaystyle
A\mathbf{x}=\lambda B \mathbf{x}
\)
ここで、\(A\)は\(N\times N\)の実対称行列、\(B\)は\(N\times N\)の実対称正定値行列（行列式がゼロではない）、\(\lambda, \mathbf{x}\)はこの問題の解であり、固有値、固有ベクトルを意味します。
MKLでは、下記の順で一般固有値問題の固有値・固有ベクトルを得ます。
- 一般固有値問題を標準形式の固有値問題に縮退（変形）
- 標準形式の固有値問題を解く
ここでいう標準形式の固有値問題とは、下記の形を持つ固有値問題です。
\(\displaystyle
A\mathbf{x}=\lambda \mathbf{x}
\)
ここで、\(A\)は\(N\times N\)の実対称行列です。
一般固有値問題から標準形式の固有値問題への式変形は、単純には両辺に左から\(B\)の逆行列\(B^{-1}\)を書ければ良いです。
ただし対称行列の逆行列は対称行列となりますが、この方法では\(B^{-1}A\)の計算を実施すると対称行列では無くなってしまうので、あまり良い方法ではありません。
また、数値計算においては逆行列をあらわに求めることはあまり意味がなく、内部的には例えばコレスキー因子分解を利用して標準形式の固有値問題に焼き直しています。
詳細は本稿のpdf、または
桂田祐史著, 『一般化固有値問題』http://nalab.mind.meiji.ac.jp/~mk/labo/text/generalized-eigenvalue-problem.pdf
をご参照ください
プログラム
MKLを使用して実対称行列を対象にする場合、?potrfと?sygstを用いて、一般固有値問題から標準形式に変形します。
変形後、通常の固有値問題となりますので、?syevdなりで得れば良いです。
下記のプログラムで一般固有値問題を解くことができます。
https://slpr.sakura.ne.jp/qp/supplement_data/diagonalize/main.f90
MKLにリンクして実行すると下記の結果を得ます。
$ ./a.out
-1.1521485211112101
1 -0.58476768299560977
1 -0.80775482423872369
1 1.0000000000000000
-0.33168880188026734
2 -12.704343950958979
2 9.0124895755548664
2 1.0000000000000000
1.2162316891886606
3 1.2579365740025481
3 0.69934198729297192
3 1.0000000000000000
$
-1.1521485211112101
1 -0.58476768299560977
1 -0.80775482423872369
1 1.0000000000000000
-0.33168880188026734
2 -12.704343950958979
2 9.0124895755548664
2 1.0000000000000000
1.2162316891886606
3 1.2579365740025481
3 0.69934198729297192
3 1.0000000000000000
$
信号と窓関数
以下のPDFにまとめました。
https://slpr.sakura.ne.jp/qp/supplement_data/signal/signal.pdf
周期的な信号に含まれるエネルギーは無限となってしまいます。
これは信号が無限続くためであり、意味がある量は時間当たりのエネルギー、すなわちパワーが重要な指標となります。
また、パワーを測定するためには無限の時間測定を実施しなければなりませんが、現実で測定を行う場合、必ず有限の時間で行われます。
そのため、有限の時間で行われた測定結果を無限に続く信号の結果に焼き直す必要があります。
無限の信号を切り出す操作を、信号に窓関数を掛ける、と表現します。
有限の時間の場合、歪められることを意味するため、この両者の関係は正確に対応付けなければなりません。
本稿はこの対応付けについて言及いたします。
また、窓関数の選び方によって本来の信号の歪められ方が変わってきます。何かの特徴が無限の信号を測定した場合に限りなく近くなる窓関数や、別の特徴が近づく窓関数などがあります。
上記のPDF内に示したFortran90によるプログラムは、以下においてあります。
https://slpr.sakura.ne.jp/qp/supplement_data/signal/signal_spectrum.tar.gz
（以下、PDF内の抜粋です。）
thinkpadとeGPUの接続が途切れる現象
現象
ThinkPadをWorkstationドック2を利用してThunderbolt3でeGPUを接続し、外部ディスプレイに出力しています。
1~5時間程度はeGPUを認識して正しく動作します。
その後突然、外部ディスプレイが数秒固まり『外部GPUは未接続です』と通知が鳴り、Thinkpad本体のみに画面出力がされます。
この時、外部ディスプレイには固まった瞬間の画面が表示されたままになりますが、外部ディスプレイは全く操作ができません。
固まった状態で、eGPU-Workstation ドック 2の間のケーブルを抜き差しすると再び外部接続は戻りますが、数分で同様の現象が発生し固まります。
固まった状態で放置すると、数分後に勢いよくeGPUファンが回り始めます。
PCの再起動をすると、再び1~5時間程度はeGPUを認識して正しく動作しますが同様の現象が起こります。
固まった状態では、デバイスマネージャー上でもeGPUに搭載されているGPUの項目が存在しません。内部グラフィックスしかありません。
解決方法
ThinkPad Thunderbolt 3 Workstation ドック 2のファームウェアをアップデートすると治るっぽいです。
毎日必ず１回は突然接続され無くなる現象が、ファームウェアアップデートした2022/10/14からぱったりと無くなりました。
母数は１です。
環境と状況
環境
品名： ThinkPad X1 Carbon (2019)
OS: Windows 11 Pro 64-bit
eGPU Box: Razer Core X
GPU: GeForce RTX 3060 Ti VENTUS 2X 8G OCV1
接続: ThinkPad Thunderbolt 3 Workstation ドック 2を利用したThunderbolt接続
出力: eGPU BoxのGPUから外部ディスプレイに出力
調査・試したこと
どうやら調べていくと、eGPUの電源周りが原因だよーみたいな記述はありましたが、同時にそれでは治らないという情報もありました。
ケーブルに触らずとも再起動でeGPUを再び認識してくれることから、Thunderbolt3周りを疑いました。
eGPU-Workstation ドック 2の間のThunderboltケーブルを変える
ケーブルが破損しており、時々通信がうまくいかなくなるのかな、と思いましたが全く変わりませんでした。
windowsの電源オプションを高パフォーマンス設定にする
高パフォーマンスモードは隠されているので、レジストリをいじって変更しましたが変わりませんでした。
windowsの電源オプションの詳細で、設定を変える
何かしらの原因で、eGPUがスリープモードに入るように信号が送られているのかと思いましたが、違いました。
これも隠されているので、レジストリをいじって項目を出現させ、
・『USBのセレクティブサスペンドの設定』を無効
・『PCI Express』→『リンク状態の電源管理』をオフ
にしましたが変わりませんでした。
振動関数のphase unwrappnig
phase unwrapping
phase unwrappingという処理があります。
これは、振動関数から位相を抽出しよう、ということを実現する処理です。
具体的に問題を書けば、関数
\(\displaystyle
y(x)=\sin(\phi(x))
\)
があり、\(y(x)\)だけが分かっているときに、\(\phi(x)\)を求める、という問題です。
仮定として、\(\phi(x)\)は滑らかな関数であるとします。
逆関数を作用させれば良いということはすぐに思いつきます。つまり、\(\sin\)の逆関数である\(\sin^{-1}\)を作用させればよく、
\(\displaystyle
\begin{align}
\sin^{-1}y(x)&=\sin^{-1}\sin(\phi(x)) \\
&=\phi(x)
\end{align}
\)
を期待します。
しかしながら、ここで問題が生じます。
それは、\(\sin^{-1}(x)\)の値域は\([-\pi/2,\pi/2]\)ですので、この範囲に押し込まれてしまうということです。
もし\(\phi(x)\)が\([-\pi/2,\pi/2]\)の範囲以外にはない、という仮定があるならば話は別ですが、
通常は\(\phi(x)=[-\infty, \infty]\)ですので、\(\sin^{-1}(x)\)を作用させた場合、値域の端で位相に不連続が生じることになります。
つまり、ただ単に\(\sin^{-1}\)を作用させただけでは、\(\phi(x)\)が滑らかである、という条件に矛盾することになります。
しかしながら、\(\sin^{-1}\sin(\phi(x))\)と\(\phi(x)\)は全く無関係なもの、というわけではありません。
\(
\begin{align}
\sin(\theta)&=-\sin(-\theta) \\
\sin(\theta)&=\sin(\theta+2n\pi), ~~~(n=0,\pm 1,\pm 2,\cdots)
\end{align}
\)
の性質があるため、\(\sin^{-1}\cos(\phi(x))\)の角度を負に取ったり、適当に\(2n\pi\)を足したり引いたりすれば、どこかに元の\(\phi(x)\)と一致する組み合わせが見つかるはずです。
このように、関数の自由度を一つに決めて、制限された関数の値域を元に戻すことをunwrappingと言います。
位相の場合は特にphase unwrappingと呼ばれます。
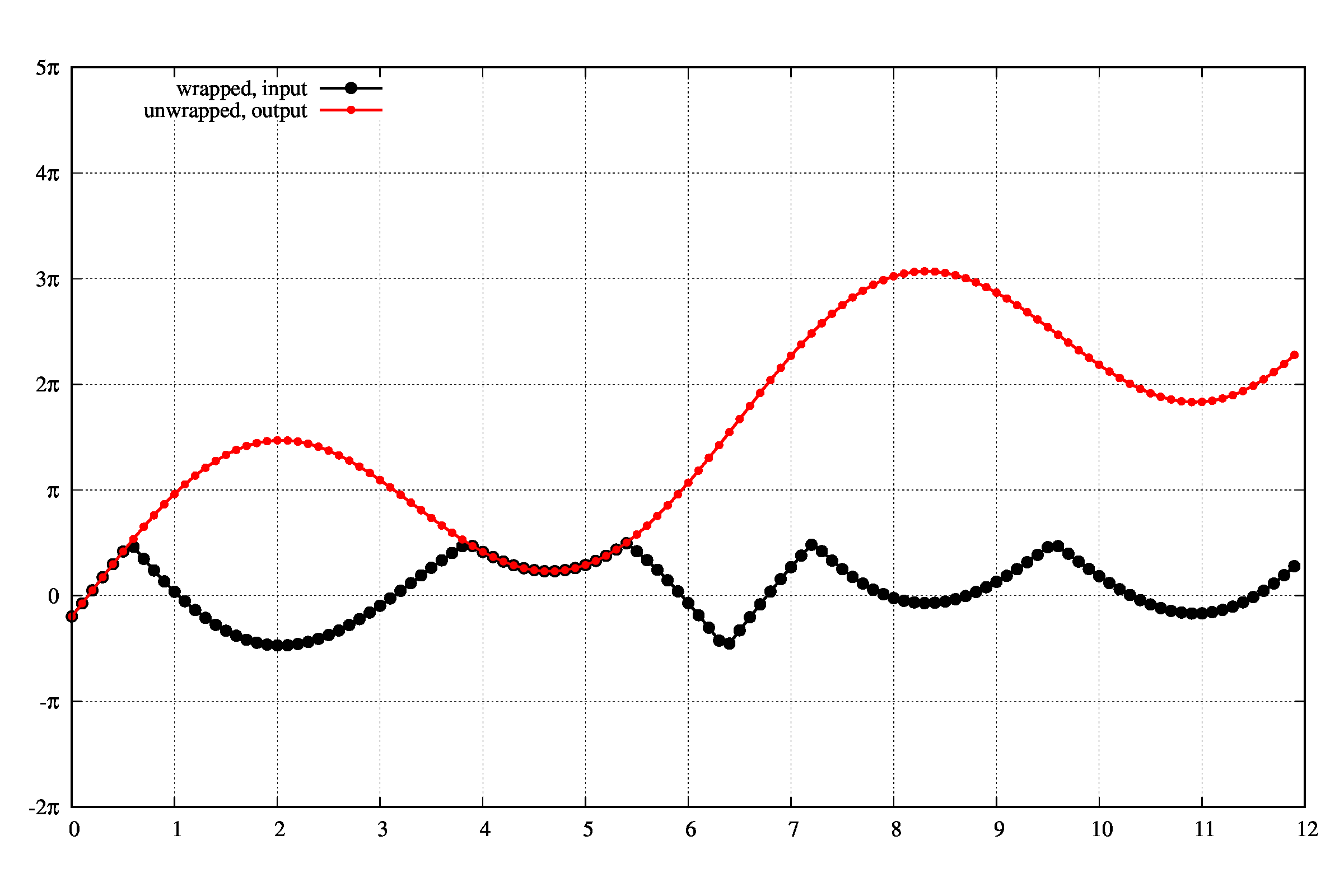
先にどのようなことを考えるか図示してみます。
入力は下の図の黒線で、ここから赤線を復元できるか？という問題です。
どのように\(\phi(x)\)と一致する組み合わせ見つけるかは様々な方法が考えられますが、愚直な方法で実装しましょう。
ここでは一例として、\(\phi(x)\)は滑らかである場合を考えて、補外によってphase unwrappingを行う方法を実装してみます。
方針
滑らかに接続できたことを考えたとしても、絶対的な位相の量は分からないので、適当な\(x_0\)における位相の値\(\sin^{-1}\sin(\phi(x_0))\)を基準として、その位置から滑らかにつながることを想定します。
以下の仮定の下で考えます。
- 離散的な\(y(x_n)=\sin^{-1}\sin(\phi(x_n)), (n=1,2,\cdots,N)\)が等間隔で与えられている。
- 入力\(y(x_n)\)の値域は\([0,\pi]\)または\([-\pi/2,\pi/2]\)
- \(\phi(x)\)は滑らかであること
- \(\phi(x)\)が局所的には2次程度の多項式で書けること
まず、基準点より一つ進んだ点の候補(\(\sin(\theta)=-\sin(-\theta), \sin(\theta)=\sin(\theta+2n\pi)\)の関係から考えられるもの)を挙げ、その中から期待されるであろう補外の値に最も近い点がunwrappingされた点だ、と考えます。
unwrapされる候補の点を挙げる
左側の元の関数\(y(x_n)\)から、右のように候補を生成します。候補は、これまでにunwrapされた関数を値の周辺のみを候補とします。
補外と上手くいかない場合
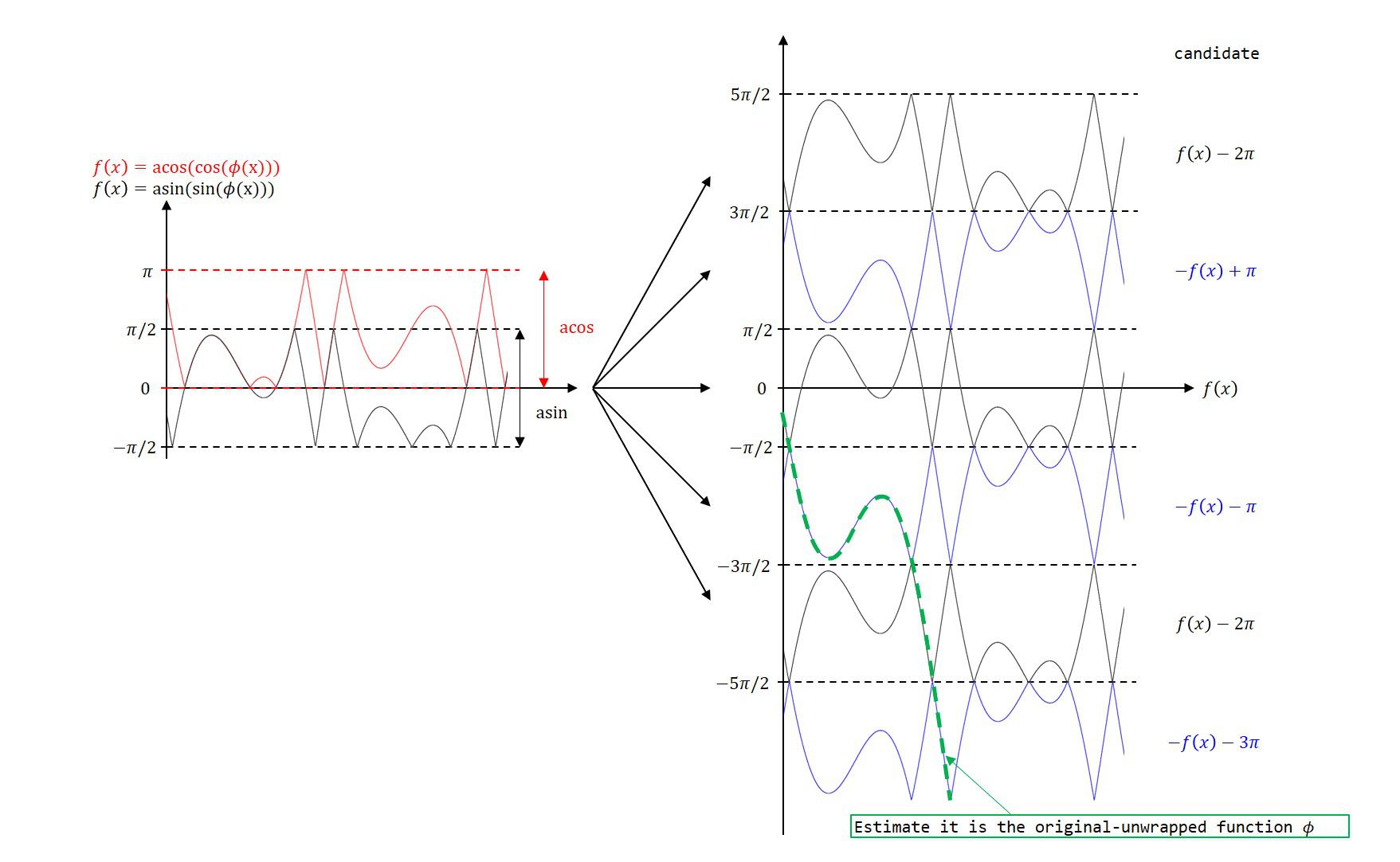
基本的なアイデアは下図左側で、これまでにunwrapされた点を元に次の点を予測し、それに最も近い候補点がunwrapの値とします。この補外によって、\([-\pi/2,\pi/2]\)ないし\([0,\pi]\)から\([-\infty, \infty]\)の領域に拡張できます。
また、異なる候補と接近する境界付近では間違えて予測する可能性があります。それは右のような状況です。
これは補外が正しく行われないことが理由なので、逆向きにも次の点を予測し、その平均を取ることで精度が上がることを期待します。
コード
Fortran90のコードです。
失敗する場合
離散した点と点の間隔が広い場合
本アルゴリズムの場合、どうしても境界付近で曲がる場合、別の領域のものをトレースしてしまう可能性があります。
厳密に傾きがゼロになり、候補が複数ある場合に正解を選び出すのは不可能です。本アルゴリズムの適用を諦めましょう。
しかしながら、元のデータ点を補間なり何かをしてマシにすることはできますので、データ点を増やして再度実行すると成功するかもしれません。
具体的に例を挙げてみます。
関数
\(\displaystyle
\begin{align}
y(x)&=acos(cos(\phi(x))) \\
& phi(x)=3.1cos(2*x)**2+exp(-0.2x)-0.8
\end{align}
\)
を考えます（適当に試していた時に失敗した関数なので、これより単純な関数でも細かく離散化されていなければ失敗するはずです）。
離散化する間隔\(\Delta x\)を\(\Delta x=0.1\)でとり、unwrapすると失敗します。
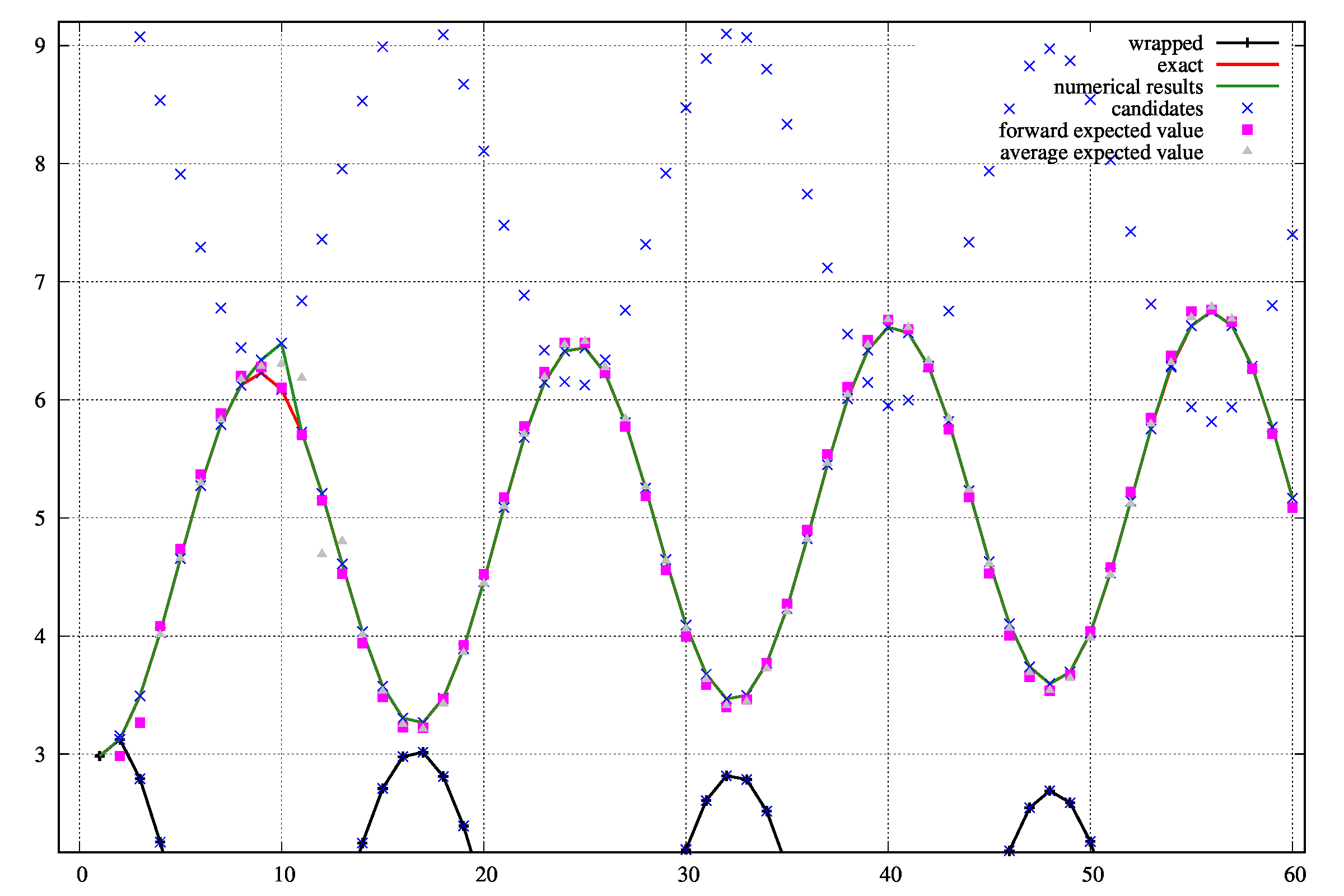
上図の横軸は離散点のインデックス、縦軸は候補やその他の情報を示しています。\(cos(x)\)の任意性は無視しています。
数値的な解は緑線であり、9,10番目の離散点（\(x=0.9, 1.0\)）で失敗しており、本来の解（赤線）とは異なる点を結んでしまっています。
しかしながら、離散化する間隔\(\Delta x\)を\(\Delta x=0.05\)でとり、unwrapすると成功します。
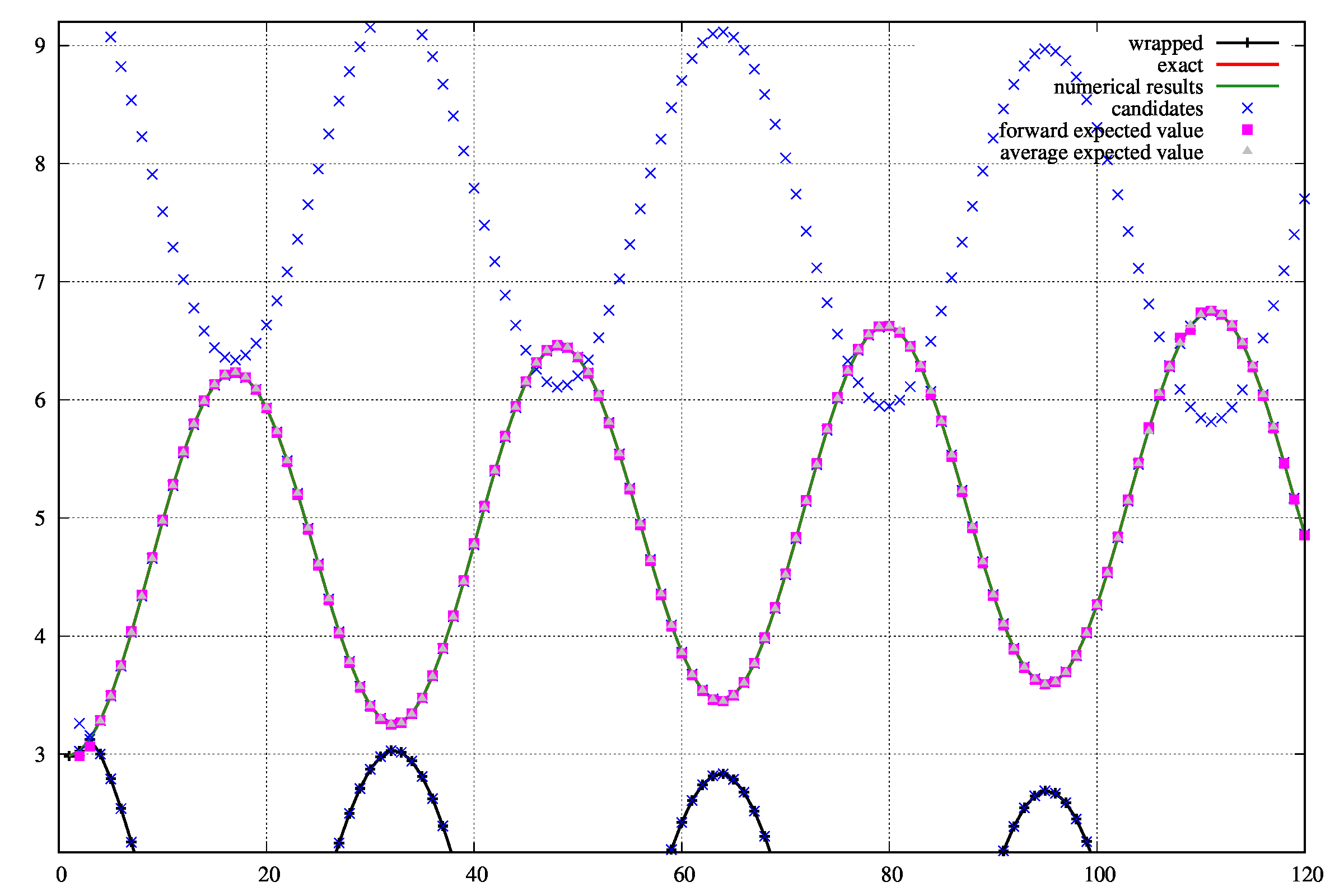
成功させるためには、できるだけ細かい間隔で離散化しましょう。
Wi-Fi接続時に、ページが開くまで数秒かかる問題の対処
事象
Wi-Fi接続時に検索、更新、リロードなど外のサーバー(www.google.comなど)にアクセスして表示するまでに5～10秒かかる。
環境
自PC --(Wi-Fi)-- ルーター --(有線)-- モデム、光回線へ
状況
- Wi-Fi接続時に発生。スマホからテザリングしても発生する
- 同ルーターの2.4GHz, 5GHzのどちらの帯域を使用しても本事象は発生する
- 同ルーターに接続している別のスマホ、別のPCでは本事象は発生しない
- 同ルーターに有線でPCに接続すると本事象は発生しない
- 接続できてからすぐに別のページを開くと数秒の間だけ本事象は発生しない
- スピードテストが実行できると高速（100Mbps前後）。pingは10ms以下で早い。
-
tracert www.google.com
を実行すると、初っ端のntt.setup (192.168.1.1)などが表示されるまでに異様に時間が掛かる(10-20秒)。
ただし、画面に表示される時間自体は10ms以下で安定している。一方でtracert -d www.google.comを実行すると、初っ端のntt.setupは一瞬で通過する。-dは名前解決を実施しないオプション。
→名前解決がうまくいっていない？
→自PCのWi-Fiアダプタに原因？
疑い
- 自PCのwifiアダプタに原因がありそう
- DNSサーバーの名前解決がうまくいっていない可能性
試したこと
PCの再起動→変化なし
PCの再起動→変化なし
Wi-Fiアダプターの更新、再インストール→変化なし
デバイスマネージャー
>ネットワークアダプター
>”Intel(R) Wireless-AC 9560 160MHz”を右クリック
>ドライバー
>ドライバーの更新、デバイスのアンインストール・インストール
PCを再起動→変化なし
Wi-Fiバンド帯の変更→変化なし
デバイスマネージャー
>ネットワークアダプター
>”Intel(R) Wireless-AC 9560 160MHz”を右クリック
>詳細設定
・802.11a/b/g ワイヤレスモード
・802.11n/ac ワイヤレスモード
の値を全通り試す。→変化なし
dns履歴のクリア→変化なし
コマンドプロンプトで以下のコマンドを実行
ipconfig /flushdns
後にPCを再起動→変化なし
IPアドレスの自動取得(DHCP)を手動で設定する→変化なし
特に変化有りませんでした.IPv4, IPv6にそれぞれ設定しましたが、本事象は改善しませんでした。
ネットワークのリセット→解決!!!
windowsの設定
>ネットワークとインターネット
>ネットワークの詳細設定
>ネットワークのリセット
>今すぐリセット
を実行→解決!!!
名前解決の手段が分からなかったので、とりあえずリセットできれば勝手に解決してくれるだろうと考えて実施しました。
※一度目にリセットを実行したとき、画面右下のWi-Fiアイコンが消えました。
しかし、デバイスマネージャーには”Intel(R) Wireless-AC 9560 160MHz”は存在していました。
再度リセット→再起動をすると元通りアイコンが復活し、本事象が解決していました。
群速度・位相速度と群遅延・位相遅延
本稿では簡単にまとめのみを載せます。
詳細は以下のPDFにまとめていますので、ご参照ください。
https://slpr.sakura.ne.jp/qp/supplement_data/groupphase_velocitydelay/group_phase_velocity_delay.pdf
本編では、なぜインパルス応答と初期状態の畳み込みが応答になるのか、なぜ畳み込みが出てくるのかを数式でおおよそ説明しています。
まとめ
分散関係\(\omega = \omega(k)\)を満たす媒質中で、波\(f\)が位置\(x\)と時間\(t\)の変数として書けている場合、
波\(f(x,t)\)は
\(\displaystyle
f(x,t)=\int \frac{dk}{2\pi} f(k) e^{ikx} e^{-i\omega(k) t}
\)
と書けます。特に\(k=k_0\)周りしか波が存在しない場合、波は
\(\displaystyle
f(x,t)=A(x-v_g t)e^{ik_0 (x-v_p t)}
\)
と書けます。ここで、\(A(x)\)は波数\(k\ll k_0\)でしか値を持たないゆっくり振動する波です。また\(v_g, v_p\)はそれぞれ群速度、位相速度を表し、以下の式で表されます。
\(\displaystyle
v_g\equiv \omega'(k_0)=\frac{d\omega}{dk}\biggr|_{k=k_0},~~~v_p\equiv \frac{\omega(k_0)}{k_0}
\)
均一な媒質中の一部に存在する別の媒質の特徴が、インパルス応答\(G(k)\)で書かれるとします。
すると、別の媒質に入射する波\(f_0(x,t)\)が、透過すると波$g(x,t)$は
\(\displaystyle
g(x,t)\Bigr|_{t\to\infty}=|G_0|A\left(x- v_g t+\varphi’_0\right)
e^{ik_0 x -i\omega_0 t + i\varphi_0}
\)
と書けます。ここで、\(G(k)=|G(k)|e^{i\varphi(k)}\)であり、
\(\displaystyle
|G_0|\equiv G(k_0),~~\varphi_0\equiv \varphi(k_0),~~\varphi’_0\equiv \frac{d \varphi(k)}{d k}\biggr|_{k=k_0}
\)
と定義しています。
ある位置でしか波形を見ない場合、相互作用の影響は時間的な遅れとして観測され、
これらを群遅延、位相遅延と呼び、次の通り定義されます。
\(\displaystyle
\begin{align}
t_g&=\frac{1}{v_g}\varphi’_0 = -\frac{d\varphi(\omega)}{d\omega}\Bigr|_{\omega=\omega_0} \\
t_p&=\frac{1}{v_p}\varphi_0 = -\frac{\varphi(\omega_0)}{\omega_0}
\end{align}
\)
別の媒質に侵入すると、波の形が崩れてしまいます。その効果は\(\varphi”(k)\)で表現することができます。
\(A(x)=e^{-(x/a)^2}\)で書かれる場合、透過した波\(g(x,t)\)は
\(\displaystyle
g(x,t)\Bigr|_{t\to\infty}=|G_0| e^{ik_0x-i\omega_0 t +i\varphi_0} \cdot
\frac{a}{(a^2-2i\varphi”_0)^{1/2}}e^{-\frac{(x- v_g t+\varphi’_0)^2}{a^2-2i\varphi”_0}}
\)
と書かれ、波の形が崩れていることが分かります。
電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式から双極子近似まで
本稿では電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式から双極子近似についてまで説明を行います.
ここでは目的と結論しか載せませんので、詳しくは以下のPDFをご覧ください。
https://slpr.sakura.ne.jp/qp/supplement_data/nrtdse_in_electromagneticfields/oneElectronAtom_electricField.pdf
目的と結論
自由粒子に対する非相対論的シュレーディンガー方程式
からスタートして, 電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式
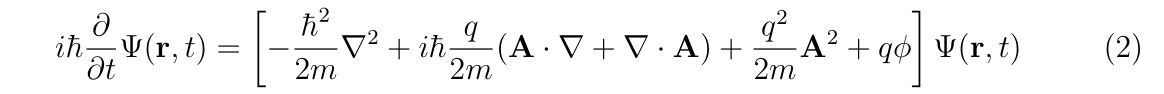
を導きます\((\mathbf{A}=\mathbf{A}(\mathbf{r},t), \phi=\phi(\mathbf{r},t))\).
その後, クーロンゲージ\((\nabla\cdot \mathbf{A}=0)\)を満たす\(\chi(\mathbf{r},t)\)を選び, かつ双極子近似\((\mathbf{A}\approx\mathbf{A}(t))\)を採用した場合に電磁場中の一電子原子の電子(電荷\(q=-e\))に対する, 速度ゲージ (Velocity gauge) , 長さゲージ (Length gauge) における真空中の非相対論的シュレーディンガー方程式
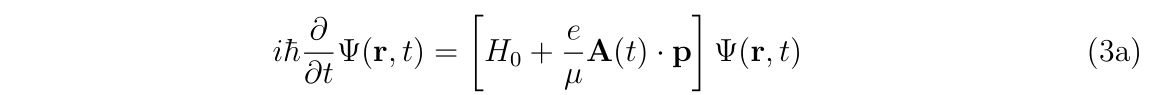
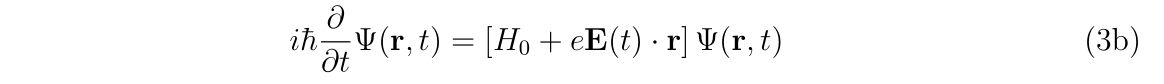
を導きます.ここで\(H_0\)は電磁場のない空間における原子のポテンシャルです. 式(3a)は速度ゲージ, 式(3b)は長さゲージにおける非相対論的シュレーディンガー方程式と呼ばれています. 双極子近似である式(3a), (3b)は, \(\mathbf{A}^2\)を含む非線形項を無視するので, 一光子過程しか考えない( 多光子過程が起こらない)という近似が入っています.
本稿の主な参考文献は,
B. H. Bransden and C. J. Joachain, 2003, “Physics of Atoms and Molecules second edition” , Prentice Hall, ISBN 0-582-35692-X
の第4章”Interaction of one-electron atoms with electromagnetic radiation”を元にしていますので, 正確な文章を希望する方はこちらをご参照ください.
クンマーの微分方程式とラゲール陪多項式
量子力学を学ぶ上で出てくる合流型超幾何関数。またはクンマー関数は学部生にとって一つのハードルとなるでしょう。
同時に、ここまで数学と物理学が密接にかかわっているんだ、ということを実感させられるきっかけでもあります。
量子力学の習い始めは、ラゲール陪多項式、ルジャンドル多項式、エルミート多項式等だけで済みますが、散乱問題などに入ると更に一般化した合流型超幾何関数が出てきます。
本稿では概要だけ示し、詳細は以下のPDFに記述しておりますので、ご覧ください。
https://slpr.sakura.ne.jp/qp/supplement_data/laguerre/LaguerrePolynomial.pdf
通常は考えない原点非正則な解も示しております。
クンマーの微分方程式
クンマー(Kummer)の微分方程式
\(
\begin{align}
\left[z\frac{d^2 w}{dz^2}+(b-z)\frac{dw}{dz}-aw\right]=0
\end{align}
\)
を考えます。クンマーの微分方程式の一般解の一つの組み合わせは、
クンマー関数\(M(a,b,z)\)とトリコミ(Tricomi)の関数\(U(a,b,z)\)を用いて
\(
\begin{equation}
w=c_1 M(a,b,z)+c_2 U(a,b,z),~~(b\ne -n)
\end{equation}
\)
と書かれます。それぞれの関数は、
\(
\begin{eqnarray}
M(a,b,z)&=&\sum_{k=0}^{\infty}\frac{(a)_k}{(b)_k}\frac{z^k}{k!} \nonumber \\
&=&1+\frac{a}{b}z+\frac{(a)_2}{(b)_2}\frac{z^2}{2!}+\cdots+\frac{(a)_k}{(b)_k}\frac{z^k}{k!}+\cdots \label{Mabz}\\
U(a,b,z)&=&\frac{\pi}{\sin(\pi b)}\left[\frac{M(a,b,z)}{\Gamma(1+a-b)\Gamma(b)}-z^{1-b}\frac{M(1+a-b,2-b,z)}{\Gamma(a)\Gamma(2-b)}\right]
\end{eqnarray}
\)
という性質を持ちます。ここで、\((a)_n\)はポッホハマー記号(Pochhammer symbol)で、
\(
(a)_k=\frac{\Gamma(a+k)}{\Gamma(a)}
\)
と書け、特に$a, k$が整数であるならば、
\(
(a)_k=a(a+1)(a+2)\cdots(a+k-1),~~(a)_0=1
\)
を意味します。
ラゲールの微分方程式
特に、クンマー方程式の引数が\(a=-n, b=\alpha+1,~(n\mbox{は0以上の整数}, \alpha\mbox{は}-1\mbox{以上の実数})\)とする場合、原点正則な解はラゲールの陪多項式で書くことができます。
ラゲールの陪多項式を級数であらわに書けば、
\(
\begin{align}
L_n^{(\alpha)}(x)=\sum_{m=0}^{n}(-1)^m\binom{n+\alpha}{n-m}\frac{1}{m!}x^m
\end{align}
\)
となります。
ちなみに、ラゲールの微分方程式の原点非正則な解は
\(
\begin{eqnarray}
&&U'(-n,\alpha+1,z) \nonumber \\
&&=\sum_{k=1}^\alpha \frac{\alpha!(k-1)!}{(\alpha-k)!(1+n)_k}z^{-k}
-\sum_{k=0}^{n}\frac{(-n)_k}{(\alpha+1)_k }\frac{z^k}{k!} (\ln(z)+\psi(1+n-k)-\psi(1+k)-\psi(\alpha+k+1)) \nonumber\\
&&\hspace{18em}+(-1)^{1+n}n!\sum_{k=1+n}^{\infty}\frac{(k-1-n)!}{(\alpha+1)_k }\frac{z^k}{k!} \nonumber \\
\end{eqnarray}
\)
と書くことができます。
参考文献
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions,
(Dover Publications Inc., New York, 1972),https://personal.math.ubc.ca/~cbm/aands/toc.htm
NIST Digital Library of Mathematical Functions
https://dlmf.nist.gov/
Internet Explorerがwindowsアクセサリに見つからない場合
まとめ
Internet Explorer 11(IE11)はここにありました。
C:\Program Files (x86)\Internet Explorer\iexplore.exe
そもそもIEが自分のパソコンにインストールされているかどうかの確認は、
コントロールパネル → プログラム → windowsの機能の有効化または無効化
より、
☑ Internet Explorer 11
にチェックが入っているかを確認してください。
チェックが入っていれば、PCにそのプログラムはインストールされています。
入っていなければ、チェックを入れ指示に従ってインストールしましょう。
IEが消えた？
推奨ブラウザがIE11であることが現在でもたまにあります。
自分のPCにも入っていると思っていましたが、なぜか検索ボックスに入れても出てこなく、
あるとされているwindowsアクセサリにもありませんでした。
例えば、以下のリンク先のように検索しても出てこなかったんです。
Windows 10 で Internet Explorer を使用する -Microsoft
・WindowsアクセサリにIE11実行ファイルが入っているか？
・そもそもPCにInternet Explorerがインストールされているか？
・インストールされているなら、実行ファイルはどこにあるか？
の順で調べていきましょう。
まずは、WindowsアクセサリにInternet Explorerの実行ファイルが入るようですので、入っているか調べましょう。
スタートボタン → Windowsアクセサリ
で調べられます。
もしなかったら、そもそもIEが自分のパソコンにインストールされているかどうかの確認します。
これは、
コントロールパネル → プログラム → windowsの機能の有効化または無効化
より、
☑ Internet Explorer 11
にチェックが入っているかで確認することができます。
チェックが入っていれば、PCにそのプログラムはインストールされています。
入っていなければ、チェックを入れ指示に従ってインストールしましょう。
WindowsアクセサリにIE11が無い場合は次の手順でみつけることができます。
WindowsアクセサリにIE11が無い場合
見つからない場合は既定のブラウザを選択して、本当に入っているかを特定、その後ファイルの場所を探しましょう。
IEを見つけるための手順は、
- 既定のwebブラウザをIEに設定
- htmlファイルを開く
- タスクマネージャーで起動中のファイルの場所を開く
- IEの場所が判明。ショートカットを作るなりする
- （既定のwebブラウザを元に戻す）
の通りです。
具体的に説明していきましょう。
既定のwebブラウザをIEに設定
スタートボタン → 設定 → アプリ → 既定のアプリ → Webブラウザー
で既定のアプリを変えてしまいます。なぜかこの画面ではIEが出てきます。
htmlファイルを開く
IEを開くために、メモ帳で「a.html」という名前のファイルを作ります（中身は空白で構いません）。
a.htmlをダブルクリックすると、既定のブラウザ(IE)で開かれます。
タスクマネージャーで起動中のファイルの場所を開く
タスクマネージャーを開き、「詳細」タブから、IEのロゴが表示された項目を右クリックし、「ファイルの場所を開く」を選択します。
すると、エクスプローラーが開きます。
IEの場所が判明。ショートカットを作るなりする
IEの実行ファイルが分かりましたので、ショートカットを作るなりしてください。
最後に、元のブラウザに既定のアプリを戻すことを忘れないようにしましょう。