非線形シュレディンガー方程式
\(
\displaystyle i\frac{\partial \Psi}{\partial t}=-\frac{1}{2}\frac{\partial^2 \Psi}{\partial x^2}-g|\Psi|^2\Psi
\)
にはある解析解が存在します。それがソリトン(soliton)解と呼ばれるもので,上式のソリトン解は
\(
\displaystyle \Psi(x,t)=\sqrt{\Omega}\ {\rm sech}\left\{\sqrt{\Omega}\left(x\sqrt{g}-\frac{gV}{2}t\right)\right\}\cdot \exp\left\{i\frac{V\sqrt{g}}{2}x-i\frac{g}{2}\left(\frac{V^2}{4}-\Omega\right)t\right\}
\)
です。(\(g>0\),\(\Omega\):ソリトンの振幅、\(V\):ソリトンの速度に関するパラメータ、ソリトン自体の速度は\(V\sqrt{g}/2\))

[adsense1]

ソリトンの歴史的背景

「非線形」とは重ね合わせの原理が成り立たない系です。

1844年、スコットランドのJ.Scott-Russellによって孤立した波(solitary wave)を観測した事が報告されました J.Scott-Russellによる報告”Report on Waves”(リンク先のSR44.pdf, 16.3MB))。
当時の認識では、波は波動方程式で記述され、その波の速度\(v\)は\(v=f\lambda\)の元、一定である。だからパルス状の波は異なる波長の波の重ね合わせで書けているはずで、時間と共に分散していくはず。なのになぜ時間が経過しても孤立した波が存在できるのか?という事で大きな論争となりました。

60年後の1895年、オランダのKortewegとde Vriesによって”浅い水の波”を記述する非線形偏微分方程式(KdV方程式)が提出され、この方程式の特解として孤立波が与えられました。
孤立波は、

1. 空間的に局在した波が、その性質(速さや形)を変えずに伝搬する
2. 孤立波は互いの衝突に対して安定であり、各々の個別性を保持する

という性質を持つ非線形波動と定義されます[1]。
2番目の、粒子のような性質を持つことから、solitary に接頭語-on をつけ、soliton(ソリトン)と名づけられました。

その後、1981年に佐藤幹夫がソリトンの統一理論(佐藤理論やKP理論)を発表しました。
これによりソリトン方程式(ソリトンを記述し，かつ厳密に解ける方程式)に決着が付きました。
ソリトン方程式は非線形なのに厳密に解ける、可積分系である。

ソリトン方程式を解く方法は([4]を引用しますが)

上で指摘したように，logistic方程式が解けるからくりとソリトン方程式が解けるからくりはよく似ています．違いは，logistic方程式が変数変換一発で線形常微分方程式になってしまったのに対し，ソリトン方程式の場合は変数変換で双線形形式になり，双線形形式の解として行列式が現れ，行列式の中身に簡単な線形方程式が現れるというところです．しかし，離散化で保存するべき構造は明らかです．まず，解の中身の線形方程式を離散化し，行列式の構造をそのまま使って双線形形式を作る．最後に変数変換して非線形のレベルに戻ればよい．

となるそうです。

また、ソリトン方程式の特徴である、無限個の対称性(無限個の保存量)は、Gardner変換という変換をすることで証明できるそうです[5]。
これ以上はこの分野の専門家ではないので話せません。

ちなみに津波もソリトンの一つとみなせます。

ソリトン解が生まれるイメージ

なぜソリトン解が生まれるのでしょうか。
今、孤立した波(空間的に凸)を考えます。この時、

エネルギー的に安定になろうとして密度を均一にするために広がろうとする効果
と
粒子間を結び付ける引力相互作用(例えば水面だったら水と水との分子間力等)のため集まろうとする効果

のつり合いによって、丁度均衡が保たれるとき、このソリトン解が生まれます。

･･･実は、ソリトン解には2種類あります。
それは明るい(Bright)ソリトン解と暗い(Dark)ソリトン解です。
今まで話していたのは全て明るいソリトン解です。
暗いソリトン解とはどういったものでしょう。
暗いソリトン解とは、ある部分が空間的に凹んでいる、孤立した解です。

エネルギー的に安定になろうとして密度を均一にするためにその凹みを埋めようとする効果
と
粒子間の斥力相互作用のために粒子間を避けようとする効果

のつり合いによって、丁度均衡が保たれるとき、この暗いソリトン解が生まれます。
暗いソリトン解が生まれるのは斥力相互作用の時で、斥力相互作用を持つ系というのは、調べた限りでは量子力学のボーズ・アインシュタイン凝縮体で、暗いソリトンは渦ソリトンという形で現れるそうです。これ以上の具体例は分かりませんでした。もしも具体例を知っているという方は教えていただければ幸いです。
暗いソリトンの解析解は参考文献[1]の本に紹介されているので、それをご参考にしてください。

非線形シュレディンガー方程式におけるソリトン解

では本題の、非線形シュレディンガー方程式における(明るい)ソリトン解を考えましょう。
下の形の非線形シュレディンガー方程式を考えます。
\(
\displaystyle i\frac{\partial \Psi}{\partial t}=-\frac{1}{2}\frac{\partial^2 \Psi}{\partial x^2}-g|\Psi|^2\Psi
\)
ここで、\(\Psi=\Psi(x,t)\)で、\(g\)は正の値で相互作用の強さ(この場合、引力相互作用)を表します。

この非線形シュレディンガー方程式のソリトン解\(\Psi(x,t)\)は、
\(
\displaystyle \Psi(x,t)=\sqrt{\Omega}\ {\rm sech}\left\{\sqrt{\Omega}\left(x\sqrt{g}-\frac{gV}{2}t\right)\right\}\cdot \exp\left\{i\frac{V\sqrt{g}}{2}x-i\frac{g}{2}\left(\frac{V^2}{4}-\Omega\right)t\right\}
\)
であり、\(\Omega\)はソリトンの振幅の大きさ、\(V\)はソリトンの速度を決めるパラメータを表します。ソリトン自体の速度は\(V\sqrt{g}/2\)となります([2]を参考)。
また、\({\rm sech}(x)\)は双曲線関数の一種(双曲線正割と呼ばれる)であり、
\(
\displaystyle {\rm sech}(x)=\frac{1}{\rm cosh(x)}=\frac{2}{e^{x}+e^{-x}}
\)
を表します。

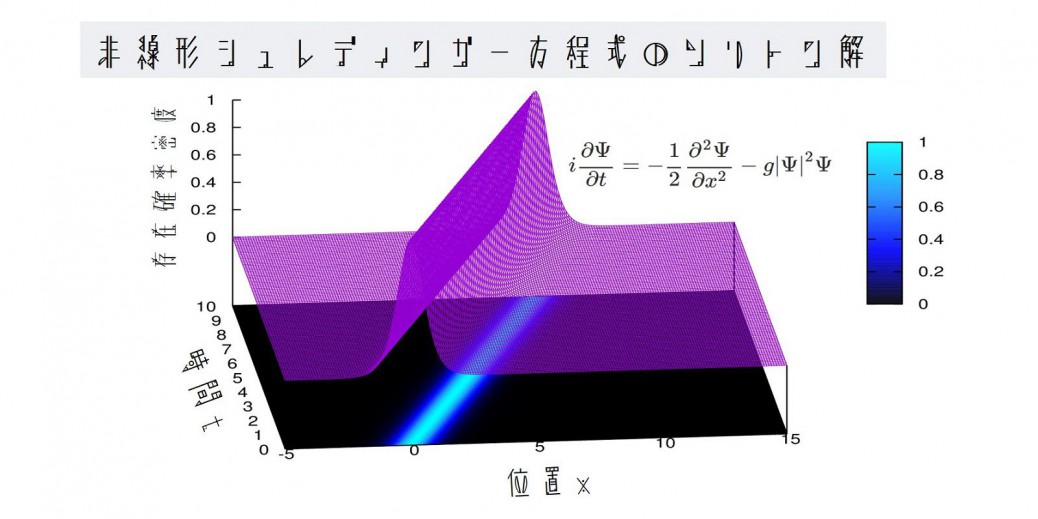
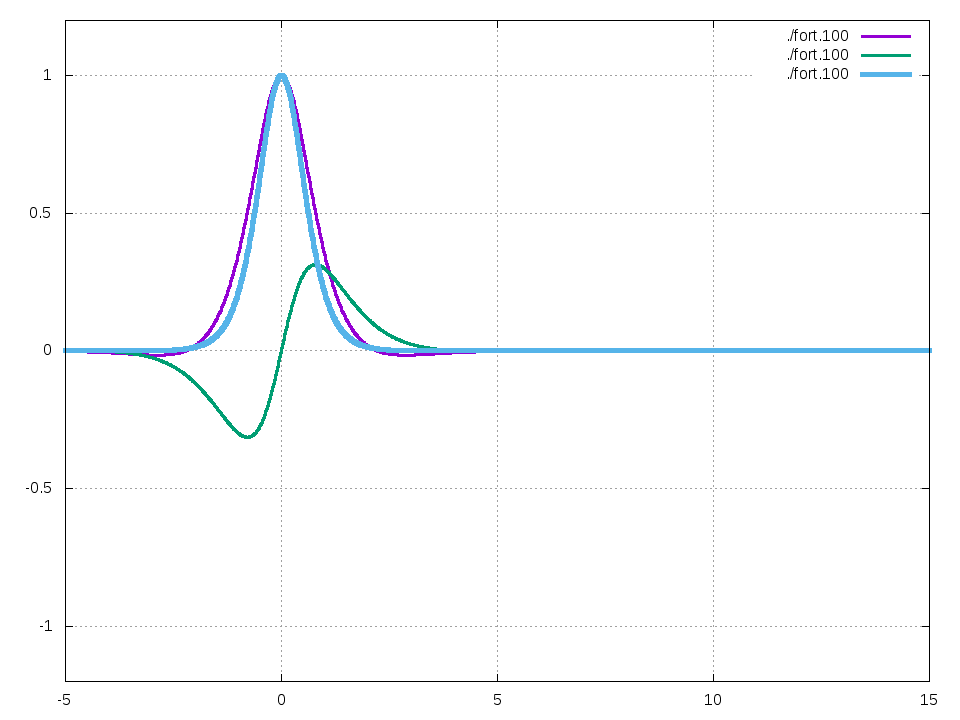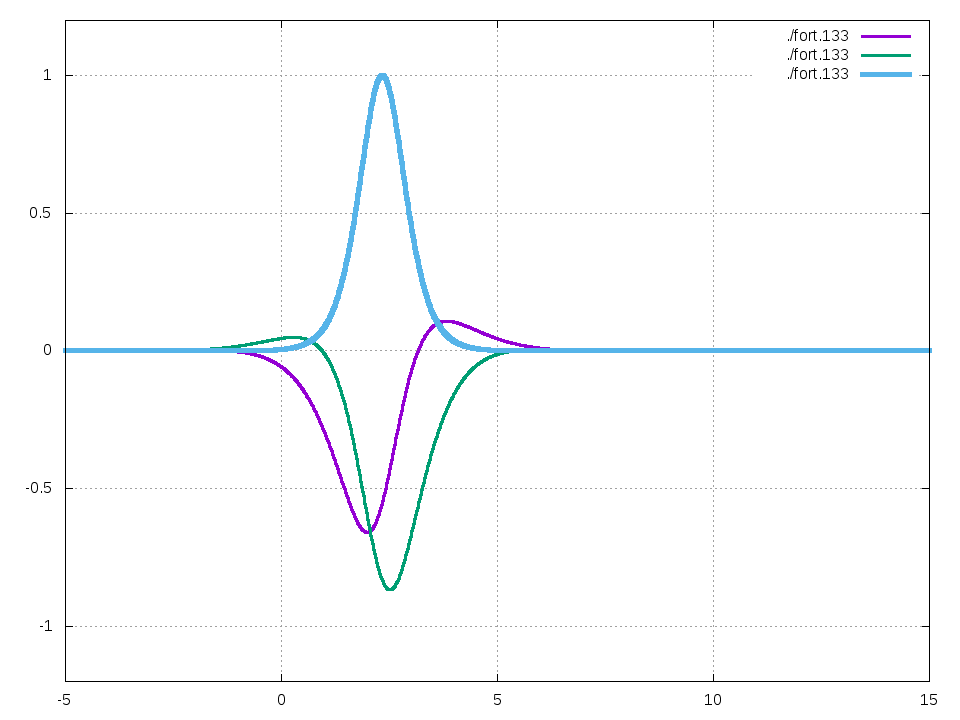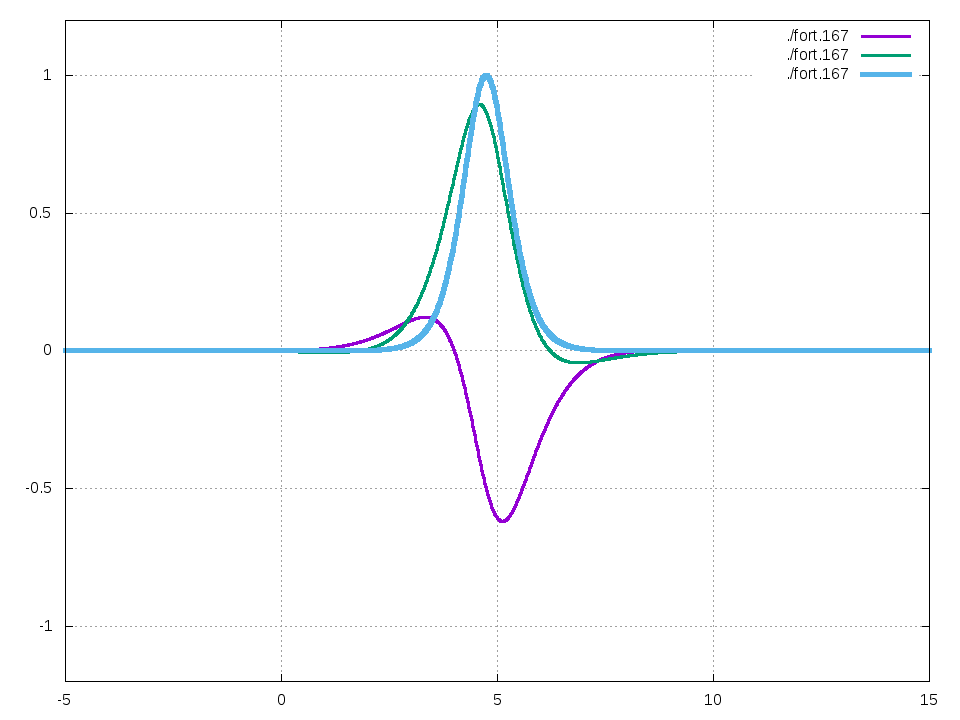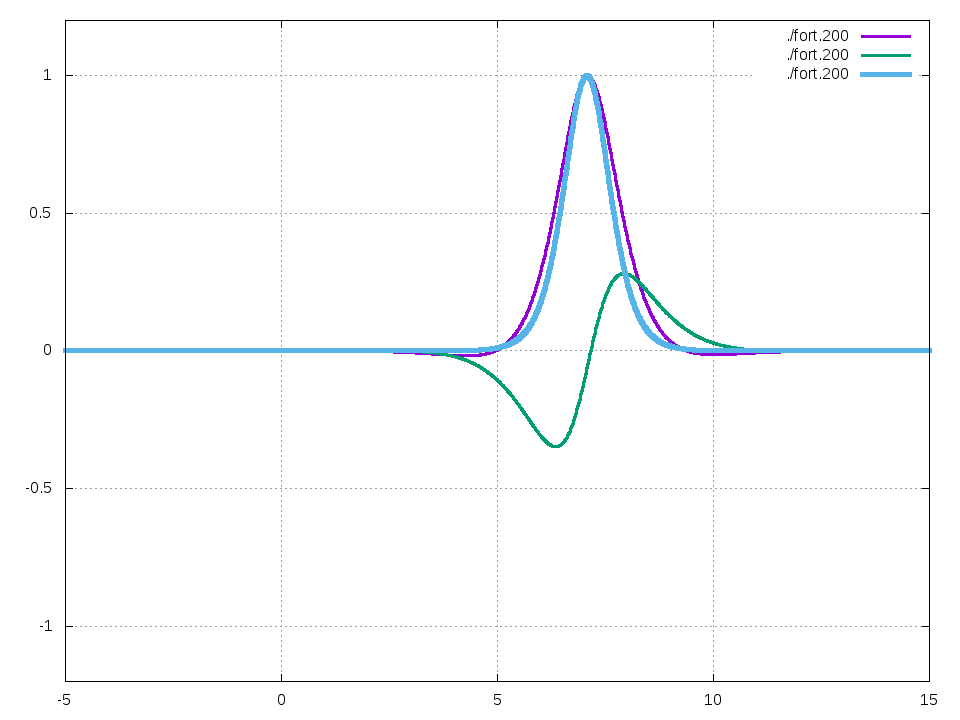
解析解のプロット

解析解をプロットします。gnuplotコードは下のほうに載せておきます。
\(g=2, V=1, \Omega=1\)とすると、以下の振る舞いが観測されます。
ここで紫はソリトン解の実部、緑は虚部、青は絶対値2乗を表します。
動画は1枚当たり原子単位系で0.1秒、合計で10秒間のシミュレーションです。
また、このソリトンの速度は\(V\sqrt{g}/2\sim 0.7071\)です。

[adsense2]

gnuplotコード

非線形シュレディンガー方程式のソリトン解(解析解)を出力します。
gnuplot上で下のスクリプトを実行してください。
(ただし、gnuplot ver4.6以降に限ります。)

もっとソリトンについて知りたい方はまず参考文献[3]を読むことをお勧めします。
その後、[4]を読み、[5]を読み、[1]の本を読むのが良いと思われます。
[3],[4]は簡単な表現を用いてソリトンとその後の発展について記述されています。

参考文献

[1]和達三樹著 『非線形波動 (現代物理学叢書) 』岩波書店 (2000年) p.7
[2]和達三樹著 『非線形波動 (現代物理学叢書) 』岩波書店 (2000年) p.29

[3]ソリトンの数学 – Researchmap
[4]ソリトン ～ 不思議な波が運んできた，古くて新しい数学の物語 ～
[5]〔連載〕非線形波動―ソリトンを中心として―第５章　逆散乱法

↑画像のフォントはキユマヤ園様による数式フォント -びゅんびゅん→SSSです！

Tweet