Schrödinger, Heisenberg, Interaction描像

Schrödinger描像、Heisenberg描像、Interaction描像というものがあります。

Schrödinger描像は波動関数による表現方法で、多くの場合で分かりやすい表現なため良く取り入れられます。
ただし、時と場合によってHeisenberg描像の方が分かりやすかったり、Interaction描像の方が最適、というときがあります。

表現方法が違うだけで同じものを表現します。

Schrödinger描像(S描像)

\(\hat{H}\)が時間依存しない場合、時刻\(t\)での波動関数は初期状態(\(t=0\))の波動関数\(\Psi_S(0)\)を用いて、
\(
\displaystyle \Psi_S(t)=e^{-i\frac{\hat{H}}{\hbar}t}{\Psi_s(0)}\ \ \ \ (1)
\)
と書くことができます。ここで添え字”\(S\)“はS描像であることを強調しています。
\(\displaystyle \hat{U}(t)＝e^{-i\frac{\hat{H}}{\hbar}t}\ \ \ (2)\)
と表記されることが多く、時間発展演算子と呼ばれています。
今、(2)の両辺を時間微分すると、\(\hat{U}(t)\)の満たす微分方程式
\(
\displaystyle i\hbar \frac{d\hat{U}(t)}{dt}=\hat{H}\hat{U}(t), \ \ \ \hat{U}(0)=1\ \ \ (3)
\)
が得られます。また、式(3)は実は\(\hat{H}\)が時間依存していても成立します。
この意味は、式(3)が時間発展演算子のより一般的な記述方法であることを意味しています。

今、Schrödinger描像で、とある演算子\(\hat{A}\)の期待値を考えます
(\(\hat{A}_S\)は時間依存してもしなくてもok)。
(例えば\(\hat{A}_S\)は位置空間で、位置演算子だったら\(\hat{x}=x\)、運動量演算子だったら\(\hat{p}=-i\hbar\frac{d}{dx}\)です。)
すると、その期待値を表す関数は時間依存し、時刻\(t\)の\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)は
\(
\begin{align}
\langle\hat{A}\rangle_t
&\displaystyle =\langle{\Psi_S}(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle e^{-i\frac{\hat{H}}{\hbar}t} \Psi_S(0)|\hat{A}_S|e^{-i\frac{\hat{H}}{\hbar}t}\Psi_s(0)\rangle
\end{align}
\)
と書けます。これがSchrödinger描像における演算子の期待値を表現しています。
Heisenberg描像(H描像)

時刻\(t\)でのHeisenberg描像の波動関数\(\Psi_H(t)\)の定義は
\(
\begin{align}
\Psi_H(t)&=e^{i\frac{\hat{H}}{\hbar}t}\Psi_S(t) \\
&=e^{i\frac{\hat{H}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0) \\
&=\Psi_S(0)
\end{align}
\)
です。
Heisenberg描像で、\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)を考えましょう。
\(
\begin{align}
\langle\hat{A}\rangle_t&=\langle\Psi_S(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_S(t)|e^{-i\frac{\hat{H}}{\hbar}t}e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}e^{i\frac{\hat{H}}{\hbar}t}|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_H(0)|\hat{A}_H(t)|\Psi_H(0)\rangle
\end{align}
\)
すなわち、S描像の演算子\(\hat{A}_S\)との間には、
\(
\hat{A}_H(t)=e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}
\)
という関係があるのです。

では、H描像で演算子\(\hat{A}_H(t)\)の時間依存性はどうなるのでしょう。
上の式を両辺微分して\(i\hbar\)を掛けると、
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{A}_H(t)&=
-\hat{H}e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}
+e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}\hat{H} \\
&=-\hat{H}\hat{A}_H(t)+\hat{A}_H(t)\hat{H} \\
i\hbar\frac{d}{dt}\hat{A}_H(t)&=\left[\hat{A}_H(t), \hat{H}\right]
\end{align}
\)

もしも、\(\hat{A}_S\)が時間依存する形だったら
\(
\displaystyle i\hbar\frac{d}{dt}\hat{A}_H(t)=\left[\hat{A}_H(t), \hat{H}\right]+i\hbar \frac{\partial \hat{A}_H(t)}{\partial t}
\)
と書けます。
Interaction描像(I描像)

前提がありまして、系のハミルトニアン\(\hat{H}\)を\(\hat{H}=\hat{H}_0+\hat{V}\)と分けます。
そして、\(\hat{H}_0\)の時間発展は分かっているものとします。

この時、時刻\(t\)でのInteraction描像の波動関数\(\Psi_I(t)\)の定義は
\(
\begin{align}
\Psi_I(t) &= e^{i\frac{\hat{H_0}}{\hbar}t}\Psi_S(t) \\
&(= e^{i\frac{\hat{H_0}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0) )
\end{align}
\)
です。
このInteraction描像の波動関数の意味を簡単に説明すると、
\(\Psi_I(t)\)は、ある時刻で、S描像の波動関数を\(e^{-i\frac{\hat{H}}{\hbar}t}\)に従って時間を進める方向に時間発展させる部分と、\(e^{i\frac{\hat{H}_0}{\hbar}t}\)に従って時間を戻す方向に時間発展させる部分の２つがある、ということです。
詳しくは後ほど述べます。

I描像での演算子\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)はどうなるのでしょう。
\(
\begin{align}
\langle\hat{A}\rangle_t&=\langle\Psi_S(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_S(t)|e^{-i\frac{\hat{H}_0}{\hbar}t}e^{i\frac{\hat{H}_0}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}_0}{\hbar}t}e^{i\frac{\hat{H}_0}{\hbar}t}|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_I(t)|\hat{A}_I(t)|\Psi_I(t)\rangle
\end{align}
\)
と書けます。

すなわち、I描像では演算子が時間依存し、波動関数も時間依存します。
よって、
Interaction描像での演算子\(\hat{A}_I(t)\)の時間依存を記述する方程式と、
Interaction描像での波動関数\(\Psi_I(t)\)の時間依存を記述する方程式
があり、それらを求めてみましょう。
- 演算子\(\hat{A}_I(t)\)の時間依存
  
  \(
  \hat{A}_I(t)=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}_0}{\hbar}t}
  \)
  演算子の期待値は上式の通りであり、もしも\(\hat{H}_0\)が時間依存しない場合、Heisenberg描像で\(\hat{H}\to \hat{H}_0\)と置き換えたものと同じ形になります。すなわち、
  \(
  \displaystyle i\hbar\frac{d}{dt}\hat{A}_I(t)=\left[\hat{A}_I(t), \hat{H}_0\right]
  \)
  となります。もしも\(\hat{H}_0\)が時間依存する場合は、
  \(
  \displaystyle i\hbar\frac{d}{dt}\hat{A}_I(t)=\left[\hat{A}_I(t), \hat{H}_0\right]+i\hbar \frac{\partial \hat{A}_I(t)}{\partial t}
  \)
では、I描像で波動関数\(\Psi_I(t)\)が満たす運動方程式はどうなるでしょう。
I描像の波動関数の定義式に左から\(e^{-i\frac{\hat{H_0}}{\hbar}t}\)を掛けると、
\(
\Psi_S(t) = e^{-i\frac{\hat{H_0}}{\hbar}t}\Psi_I(t)
\)
であり、これをS描像のSchrödinger方程式に代入します。
\(
\begin{align}
& i\hbar \frac{\partial}{\partial t}\left(e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)\right)
=\hat{H}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
& i\hbar \left[-\frac{i}{\hbar}\hat{H}_0 e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)+e^{-i\frac{\hat{H}_0}{\hbar}t}\frac{\partial \Psi_I(t)}{\partial t}\right]
=\hat{H}_0e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)+\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
& i\hbar e^{-i\frac{\hat{H}_0}{\hbar}t}\frac{\partial \Psi_I(t)}{\partial t}=\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
\end{align}
\)
左から\(e^{i\frac{\hat{H}_0}{\hbar}t}\)を作用させると、
\(
\displaystyle i\hbar \frac{\partial \Psi_I(t)}{\partial t}=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)
\)
ここで、Interaction描像の演算子\(\hat{H}_I(t)\)を
\(
\displaystyle \hat{H}_I(t)=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}
\)
と置くと、波動関数\(\Psi_I(t)\)が満たす運動方程式
\(
\displaystyle i\hbar \frac{\partial \Psi_I(t)}{\partial t}=\hat{H}_I(t)\Psi_I(t)
\)
が得られます。

さて、定義が終わったところで、Heisenberg描像とInteraction描像の意味を見てみましょう。
簡単にそれぞれの描像を説明すると、

Heisenberg描像：量子-古典対応を成す
Interaction描像：既に分かっている部分を取り除く

という特徴があります。

まずはHeisenberg描像から。
Heisenberg描像でHeisenberg描像の演算子\(\hat{A}_H(t)\)の時間発展を記述する運動方程式は
\(
i\hbar\frac{d}{dt}\hat{A}_H(t)=\left[\hat{A}_H(t), \hat{H}\right] \cdots(A)
\)
です。
今、\(\hat{A}_H(t)\)が位置演算子\(\hat{q}\)と運動量演算子\(\hat{p}\)によって表記されていると考えます。
この時、Schrödinger描像で、それぞれの演算子はハミルトニアンと
\(
\begin{align}
\left[\hat{q}_S,\hat{H}_S\right] &= i\hbar \frac{\hat{p}_S}{m} \\
\left[\hat{p}_S,\hat{H}_S\right] &= -i\hbar \frac{\partial}{\partial \hat{q}_S}\hat{H}_S
\end{align}
\)
という関係があります。
Heisenberg描像でSchrödinger描像のハミルトニアンがどう記述されるのかを考えてみると、
\(
\begin{align}
\hat{H}_S &= \frac{\hat{p}_S^2}{2m}+\hat{V}_S \\
&= \frac{1}{2m}e^{-i\frac{\hat{H}_S}{\hbar}t}\hat{p}_H^2 e^{i\frac{\hat{H}_S}{\hbar}t}+e^{-i\frac{\hat{H}_S}{\hbar}t}\hat{V}_H^2 e^{i\frac{\hat{H}_S}{\hbar}t} \\
&= e^{-i\frac{\hat{H}_S}{\hbar}t}\left( \frac{\hat{p}_H^2}{2m}+\hat{V}_H\right) e^{i\frac{\hat{H}_S}{\hbar}t} \\
\hat{H}_H&= e^{i\frac{\hat{H}_S}{\hbar}t}\hat{H}_S e^{-i\frac{\hat{H}_S}{\hbar}t} \\
&=\hat{H}_S
\end{align}
\)
となり、結局
\(
\hat{H}_S=\hat{H}_H
\)
であることが導かれます。
Heisenberg描像での位置演算子\(\hat{q}\)と運動量演算子\(\hat{p}\)の交換関係は
\(
\begin{align}
\left[\hat{q}_H,\hat{H}_H\right] &= i\hbar \frac{\hat{p}_H}{m} \\
\left[\hat{p}_H,\hat{H}_H\right] &= -i\hbar \frac{\partial}{\partial \hat{q}_H}\hat{H}_H \\
\end{align}
\)
であることが導けるため、\(\hat{q}_H\)と\(\hat{p}_H\)に関して、運動方程式に代入して
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{p}_H(t)&=\left[\hat{p}_H(t), \hat{H}_H\right] \\
&= -i\hbar \frac{\partial}{\partial \hat{q}_H}\hat{H}_H \\
\frac{d}{dt}\hat{p}_H(t)&=-\frac{\partial}{\partial \hat{q}_H}\hat{H}_H
\end{align}
\)
であり、
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{q}_H(t)&=\left[\hat{q}_H(t), \hat{H}_H\right] \\
&= i\hbar \frac{\hat{p}_H}{m} \\
\frac{d}{dt}\hat{q}_H(t)&=\frac{\partial}{\partial \hat{p}_H}\hat{H}_H
\end{align}
\)
となります。
この二つの式は、古典力学のハミルトンの運動方程式に酷似していますよね。ここからHeisenberg描像が量子-古典対応を成す、という所以になるわけです。

注意として、Heisenberg描像は、量子-古典対応を成しますが、演算子それ自身を測定することなどできないのです。あくまで期待値と対応するだけです。
また、Heisenberg描像は古典力学への回帰を見出し、エーレンファストの定理と関連します。

続いて相互作用描像です。
系のハミルトニアン\(\hat{H}\)を\(\hat{H}=\hat{H}_0+\hat{V}\)と分けます。
そして、\(\hat{H}_0\)の時間発展は分かっている時、Interaction描像の波動関数\(\Psi_I(t)\)は
\(
\begin{align}
\Psi_I(t) = e^{i\frac{\hat{H_0}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0)
\end{align}
\)
でした。じっくり見ていきましょう。
例を考えます。
\(
\displaystyle \hat{H}=\hat{H}_0+V(x)=-\frac{\hbar^2}{2m}\nabla^2+V(x)
\)
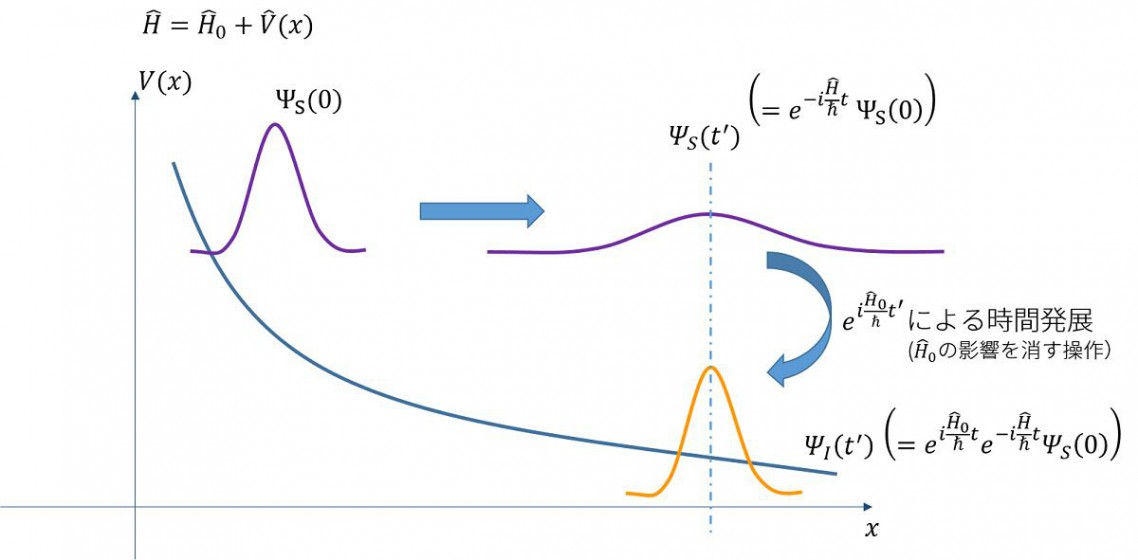
で、ポテンシャル\(V(x)\)が単調減少で図のような山なりの波形をしている場合を考えます。

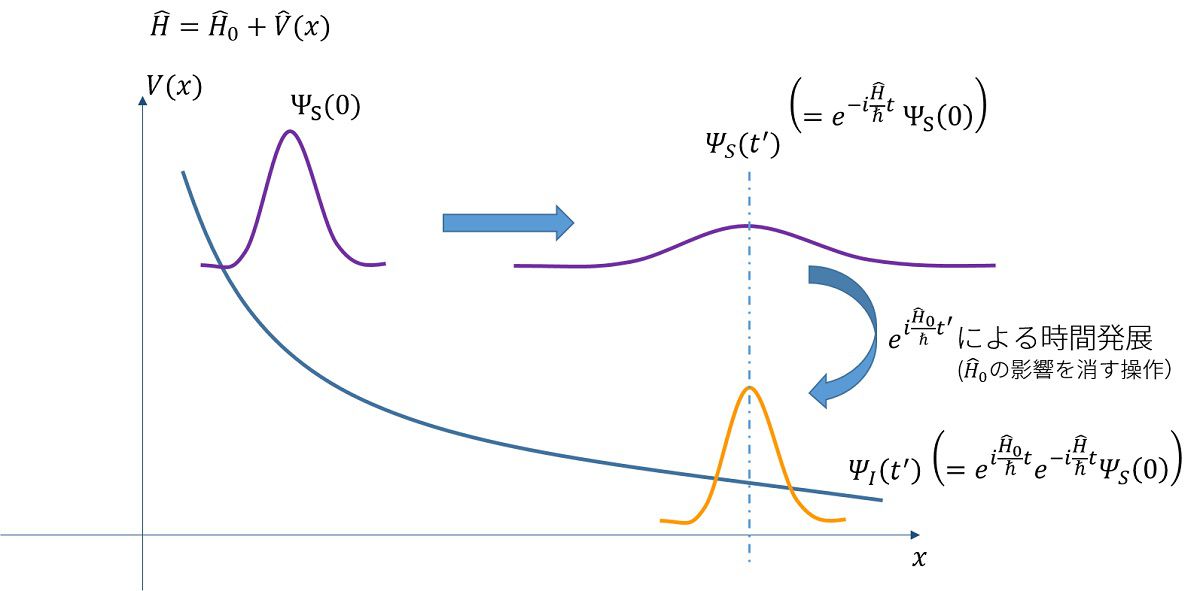
初期状態\(\Psi_S(0)\)があったとすると時間経過すると、その波動関数の形は広がりながら右へ移動します。
Interaction描像では、この、広がる、という動きと、右へ移動する、という動きが合わさったと考えます。
広がる動きは、ポテンシャルが無いときの波束の動きです。ポテンシャルがない時、右に動くことはしません。
右への動きは、ポテンシャルしか無いときの波束の動きです。質点を考えれば、ポテンシャルの山を転がり、右へ動きます。