BB弾の回転量について(実験との比較)

BB弾の回転量について,係数\(C_l\)は
\(
\begin{align}
C_l&\approx 0.12\\
\end{align}
\)
で近似できる、と実験データから求まりました。
実験データ(ハイスピードカメラによる回転量計測及び弾道データ)を提供してくださった
ガンジニア、石岡様(http://gungineer.matrix.jp/)に感謝いたします。

弾道計算に関するその他ページ
弾道計算(BB弾)の理論
 BB弾の回転量について(実験との比較)←今ここ
弾道計算(BB弾)の結果
 弾道計算の結果2, 比較と詳細データ
 弾道計算(BB弾)のコード(fortran90)
バレル内部でのBB弾の方程式

[adsense1]

対象とする問題

BB弾の運動方程式を求める事が出来ましたが、BB弾の回転量に関して計算と実験との間に4~5倍近い差が生じていました。この原因は、BB弾の回転量と発生する循環を一緒にしていたためです。式で表せば運動方程式は

・BB弾の運動方程式
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}+\left\{-6\pi \eta R |\vec{V}|-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|^2\right\}\frac{\vec{V}}{|\vec{V}|}
-C_l\left(S_p\right)\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
・BB弾の回転角速度の減衰を記述する方程式
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)

と書けます。今まで係数\(C_l\left(S_p\right)\)を1にしていました。
この係数を求める事が今回の目標です。

良く使われるパラメータにスピンパラメータ\(S_p\)なるものが存在するようで[1]、今回はこれに倣います。
これは回転球の表面での速度\(R\omega\)と飛翔速度\(v\)に関する無次元量で,
\(
S_p=R\omega/v
\)
と書かれます。
BB弾の場合、実験[2]より、おおよそ150[回転/秒, rps]ということが分かりました。
飛翔速度はおおよそ\(80[{\rm m/s}]\)と考えると、スピンパラメータの値の範囲はおおよそ
\(
\displaystyle S_p=\frac{3\times 10^{-3}{\rm [m]}\cdot 2\pi\cdot 150{\rm [/s]}}{80{\rm [m/s]}}\sim 0.0353\cdots
\)
という量になります。よって、\(C_l(S_p)\)を\(S_p=0\)回りでテーラー展開して、
\(
C_l(S_p)\sim c_0+c_1 S_p+c_2 S_p^2 +O(S_p^3)
\)
と考えられます(補足1)。

\(C_l(S_p)\)の導出

係数\(C_l(S_p)\)を以下のように求めます。

・ある既知の回転量で射出されたBB弾が描く軌道
と
・その既知の回転量を初期条件として運動方程式を解いた場合の軌道

の分散を最小にするパラメータをモンテカルロ法によって求めます。モンテカルロ法などと言っていますが、これは\(c_0,c_1\)に乱数を適当に振って良さげなものを求める、ということです。

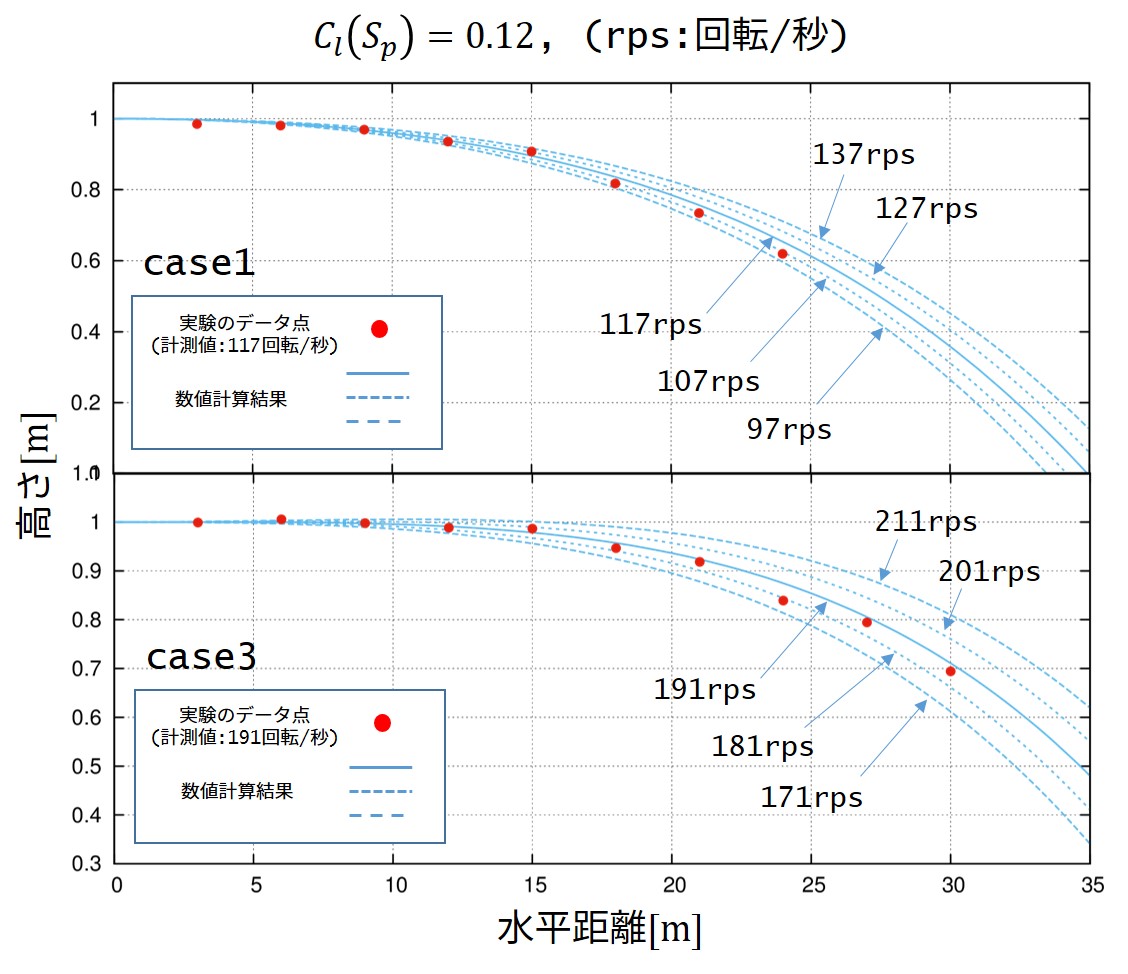
ここでは実験から得られたある3つの回転量
case1：117回転/秒
case2：147回転/秒
case3：191回転/秒
の軌道との比較を行います。

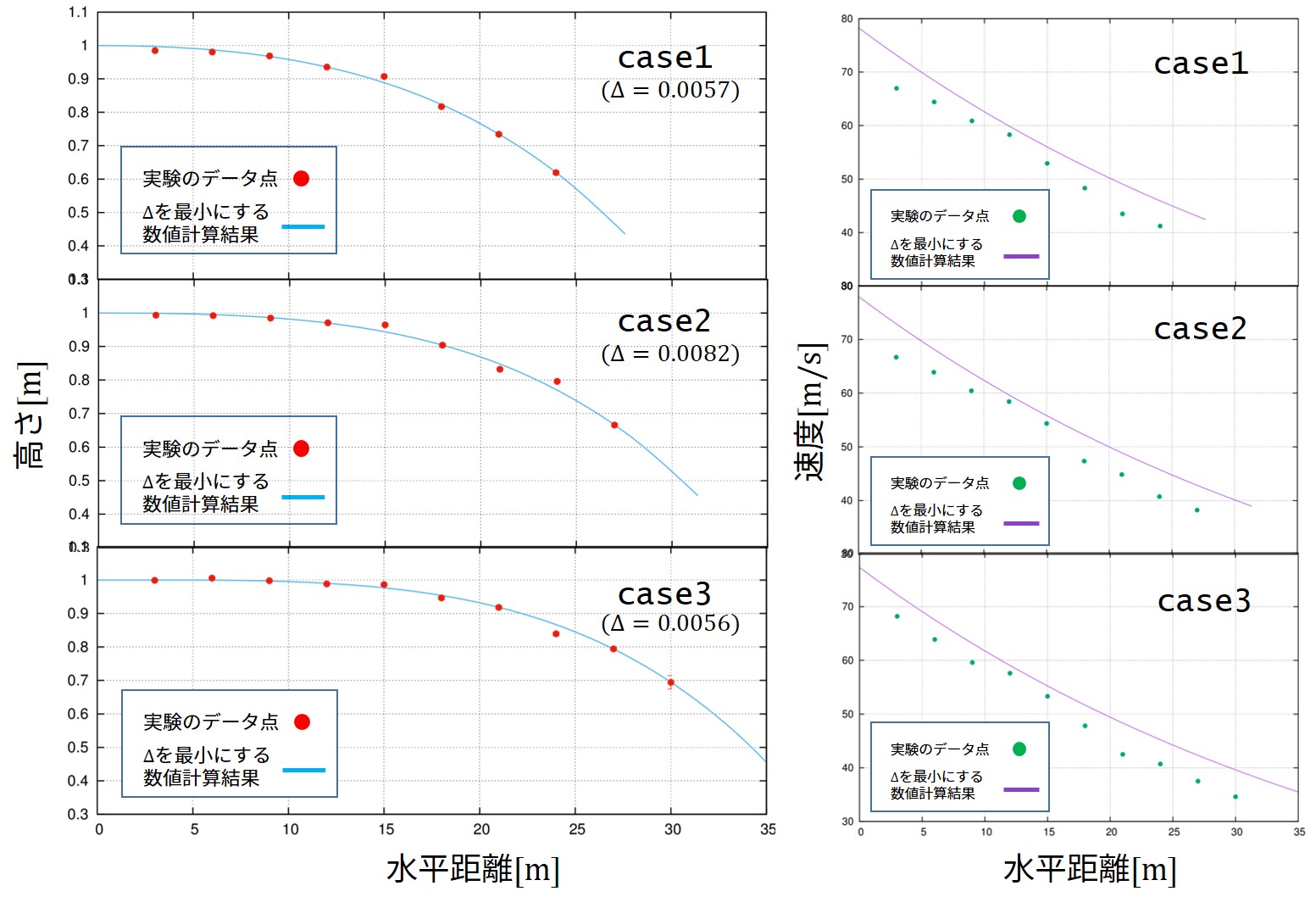
実験のデータ点\(x_i\)と数値計算でのデータ点\(X_i\)との差の2乗の平方根をデータ点数\(N\)で割ったものを\(\Delta\)と定義します。

この\(\Delta\)が最も小さくなるパラメータの組み合わせが今求めたいものです。
縦軸に\(\Delta\)、横軸に各々のパラメータ\(c_0,c_1,c_2\)を取ったものをグラフにすると以下のようになります。

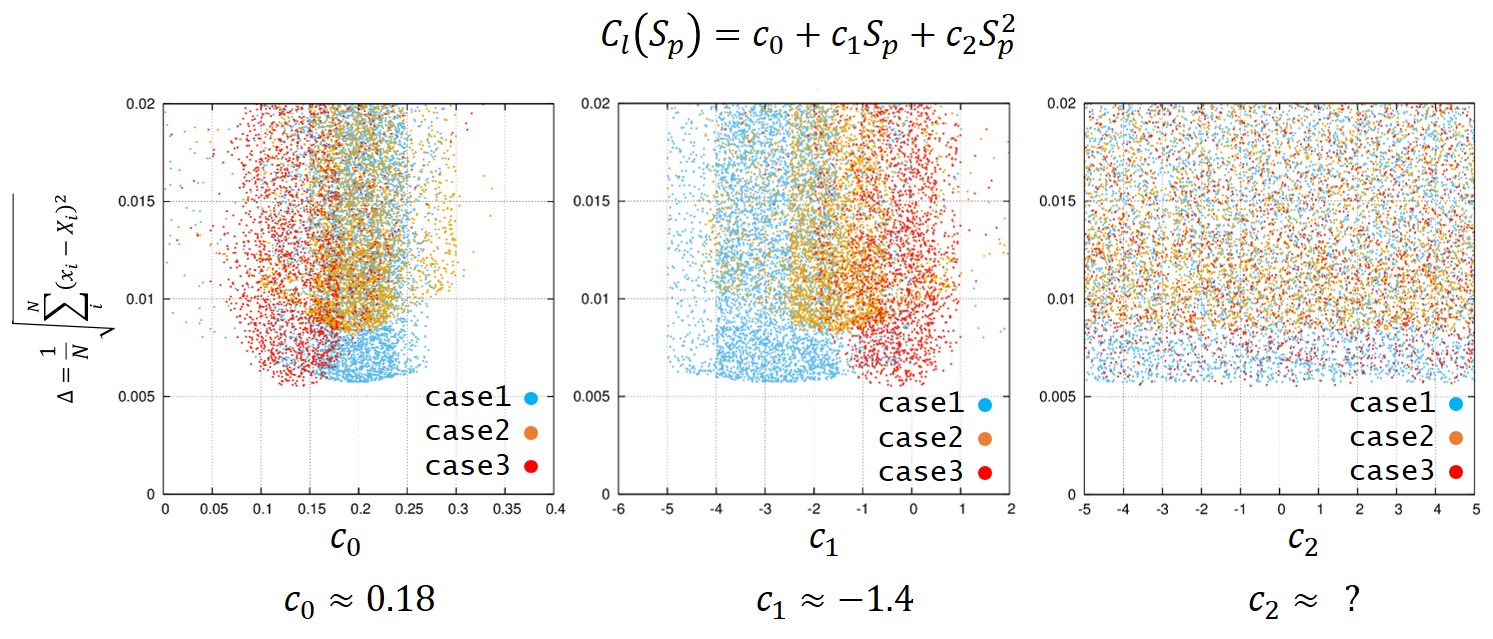
各々のcase1,case2,case3で、\(\Delta\)を最小にするパラメータで軌道と終端速度の妥当性を見てみますとこうなります。

速度が合わない原因としては恐らく、終端速度の計測機器による不具合でしょう。

なぜなら、初期速度を実験から得られたデータ値にした際、case3に対して同様にフィッティングするとばらつき具合を示す\(\Delta\)が1.9という値になってしまい、明らかに悪くなるからです。

実験のデータ点に+3[m/s]にするとおおよそ妥当なことが分かります。

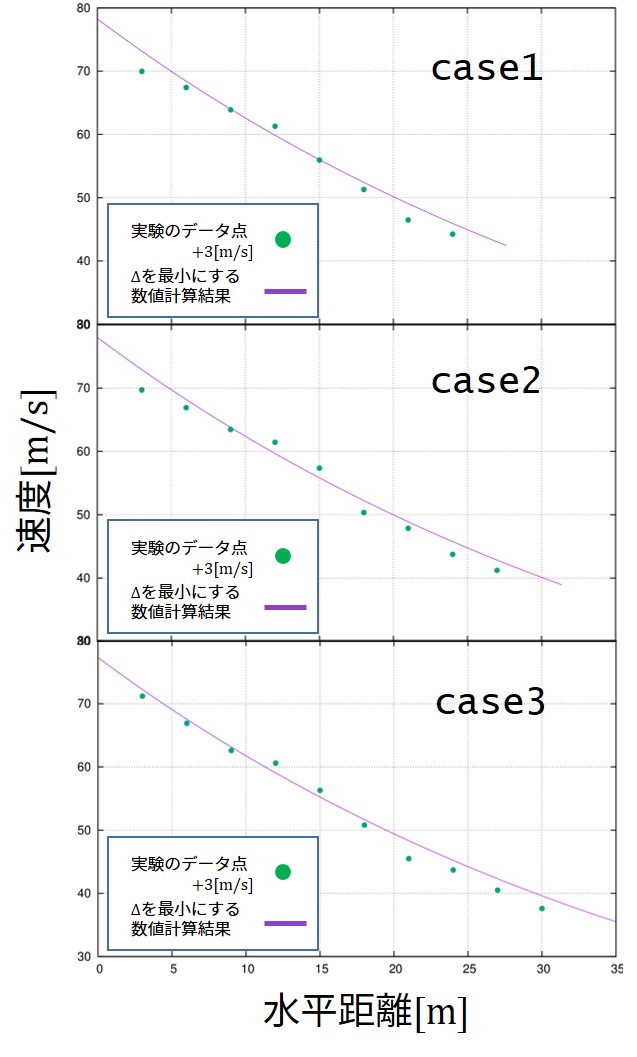
きっと計測機器の初期値がずれていただけでしょう。

\(\Delta\)の図から、最小地点3点での平均を取ればいいです。すると
\(
c_0\approx 0.18,\;\;\; c_1\approx -1.4 \;\; c_2=?
\)
と求める事が出来ました。\(c_2\)の項が求まりませんでしたので、\(c_1\)で打ち切ります。

考察

\(c_1\)で打ち切ることを考えると少し問題が生じます。今、\(c_1\)はどうやら負のようです。
と言うことは、これをこのまま高速回転する状況に使うと、回転が増えると逆に落ちやすくなる事を意味しています。\(S_p\)が上のように限定されている場合では精度よく求められますが、広い範囲ではちょっと上の級数展開式は使えません。

現実的な問題で考えましょう。
物理的に正しくなるように、係数\(C_l(S_p)\)は常に正の値でなければならないと仮定します。なので、上の級数展開はよろしくありません。
単純に定数として求めてしまいましょう。すなわち、
\(
\begin{align}
C_l(S_p)&\approx c_0
\end{align}
\)
とします。球自体の循環だけに依存するとして広い範囲で(とりあえず)使える定数を求めます。

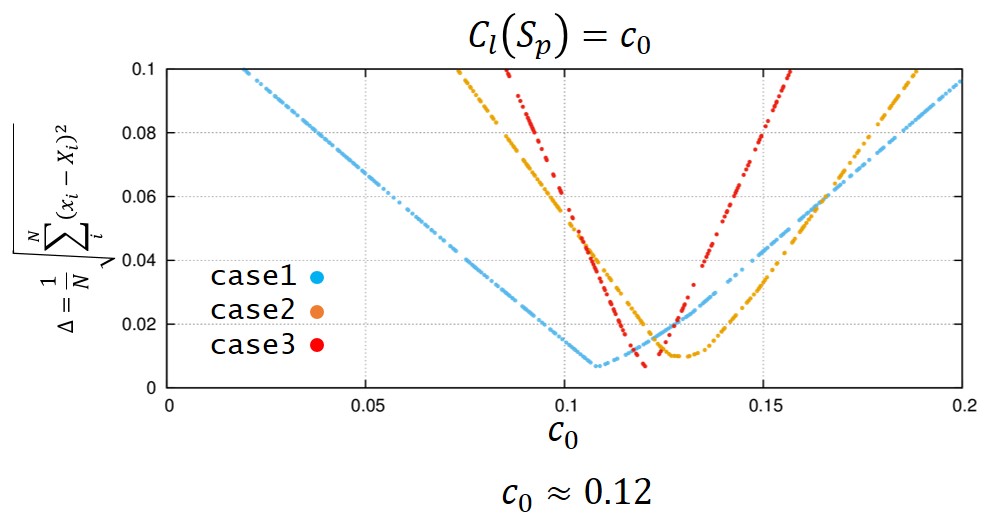
そうして実験データから\(\Delta\)を最小にする\(c_0\)を求めてやると、
\(
C_0=0.12
\)
と求まりました。
実際に\(C_l(S_p)=0.12\)で実験との比較をしてみますと、こうなります。

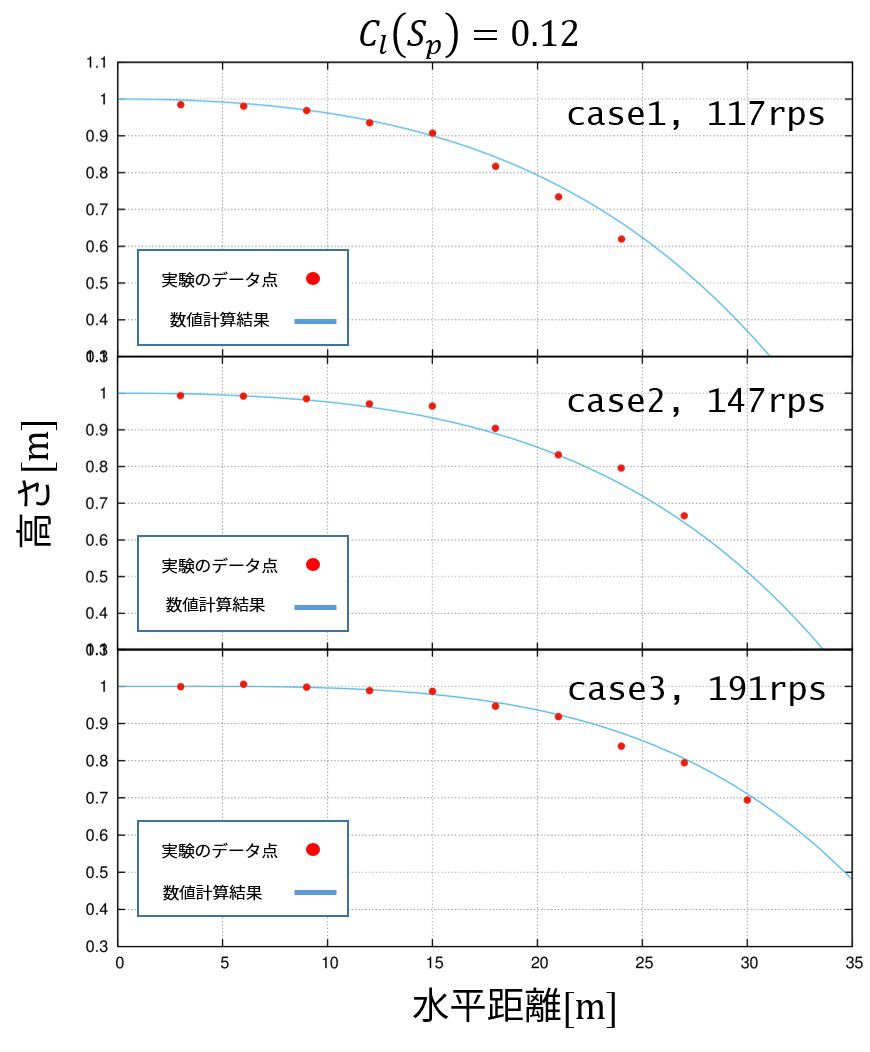
定数として考えてもそんなに悪くないと思います。
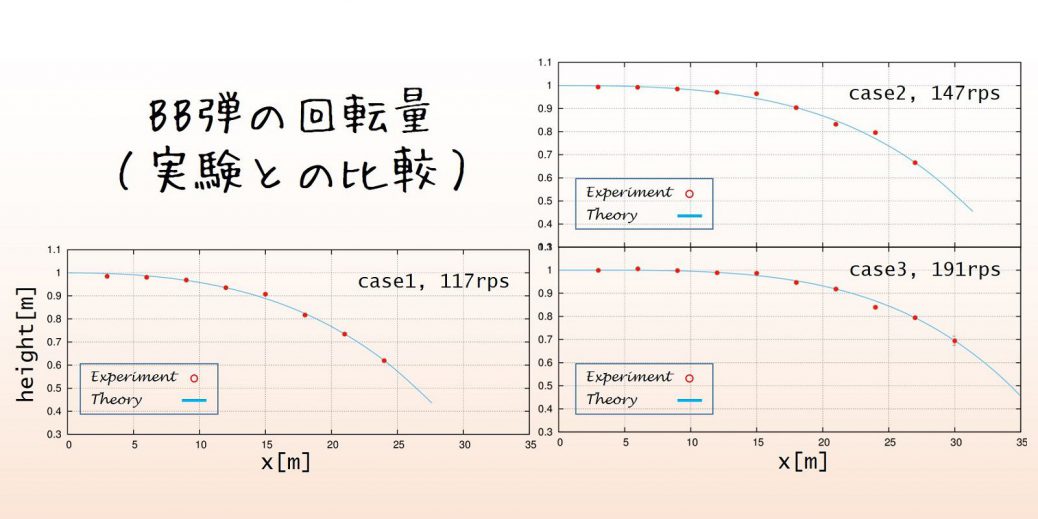
case1,case3 を用いて、\(C_l(S_p)=0.12\)の妥当性を考えてみます。
\(C_l=0.12\)として、大体どの程度の回転量の誤差に収まっているかを示したのが以下の図です。

数値計算上で求められた回転量は現実の回転量と10%程度の誤差に収まっていることが分かりました。

どれが良いかは一概には言えません。
回転量を知らなくていいなら\(C_l(S_p)=1\)で良いと思います。
回転数を大雑把にでも知りたければ\(C_l(S_p)=0.12\)を、
\(S_p\)が小さい、すなわちホップをあまりかけないで0.9J近くで飛ばす限定された状況では\(C_l(S_p)= 0.18-1.4S_p\)が良いと思います。

[adsense2]

結論

エアガンから射出された、BB弾の従う方程式は

・BB弾の運動方程式
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|^2\frac{\vec{V}}{|\vec{V}|}
-C_l\left(S_p\right)\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
・BB弾の回転角速度の減衰を記述する方程式
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)
ここで、
\(
\begin{align}
&C_l(S_p)\sim 0.18-1.4S_p+O(S_p^2) \\
&S_p=R\omega/v
\end{align}
\)
もしくは
\(
C_l(S_p)\sim 0.12
\)
で近似できる。
という結論を得ました。

最後に、実験データ(ハイスピードカメラによる回転量計測[2]及び弾道データと速度データ)を提供してくださった
ガンジニア、石岡大樹様(http://gungineer.matrix.jp/)に心より感謝申し上げます。
以下の実験時の条件は石岡様が行っていただいた条件です。

実験[2]とデータ採取時の条件

エアガン：東京マルイ　VSR-10 G-SPEC
BB弾：ギャロップ 0.3g
ハイスピードカメラ：PHOTRON MH4-10K、10000fps
データ点の採取方法：Stealth-Target ST17

室温、湿度、気圧の計測
1つのデータ点につき、30回計測

補足1

私の予測ですが、\(C_l\)の展開方法について述べておきます。
論文[1]によると、回転による揚力を私のようには書いておらず、
揚力を\(L\)と記述し、
\(
\displaystyle L=\frac{1}{2}C_l\rho U^2 A
\)
のように記述しています。ここで、\(\rho\)は空気の密度、\(U\)は球の速度、\(A\)は球の直径断面積です。
[1]では\(L\)を実験から直接求めて\(C_l\)を求めています。
この時に\(C_l\)をスピンパラメータ\(S_p\)で展開して実験データをフィッティングしているので私の計算と事情が違うのかもしれません。

[1]を頼らないことにしましょう。
物理的な予測から求めていきます。回転量依存だと考え、\(C_l(\omega)\)として考えます。
１．どんな回転量でも\(C_l\)は正である必要があります(負のマグヌス力は今回の場合発生しないと考える)。なので、
\(
C_l(\omega) > 0
\)
でなければなりません。
２．回転が非常に0に近い時、球体の循環と周りで発生する循環は一致するはずです。
なので、
\(
C_l(\omega\to 0)=1
\)
であることが予想されます。
３．回転が非常に強い場合、周辺の空気は限られるため発生する揚力は弱くなっていくはずです。
ただし、回転が無限大の時、揚力自体は発散すると予想できるので、係数\(C_L\)は揚力の発散を抑えてはなりません。なので、
\(
C_l(\omega\to\infty) = A\omega^{k},\;\;(A=\mbox{const},\;\; -1 \lt k )
\)
であるはずです。

物理的な考察から、係数\(C_l\)が満たすべき条件はこんなものでしょうか。
BB弾の回転量\(\omega\)が程々の場合は予想が出来ません。どこかにピークがあるのかもしれませんし、緩やかに減少していくだけかもしれません。
適当な関数を持ってくるのも手ですが、私は嫌います。
そんなことをやるのなら定数でいいだろうとして、
\(C_l=0.12\)と言う結論となりました。

参考文献

[1]鳴尾丈司, 溝田武人, 下園仁志, “一様気流中で高速回転するゴルフボールの空気力測定と飛しょう実験” 日本機械学会論文集 B編 Vol. 70 (2004) No. 697 P 2371-2377
[2]石岡大樹、ホップアップの回転数測定　TM VSR-10 G-SPEC