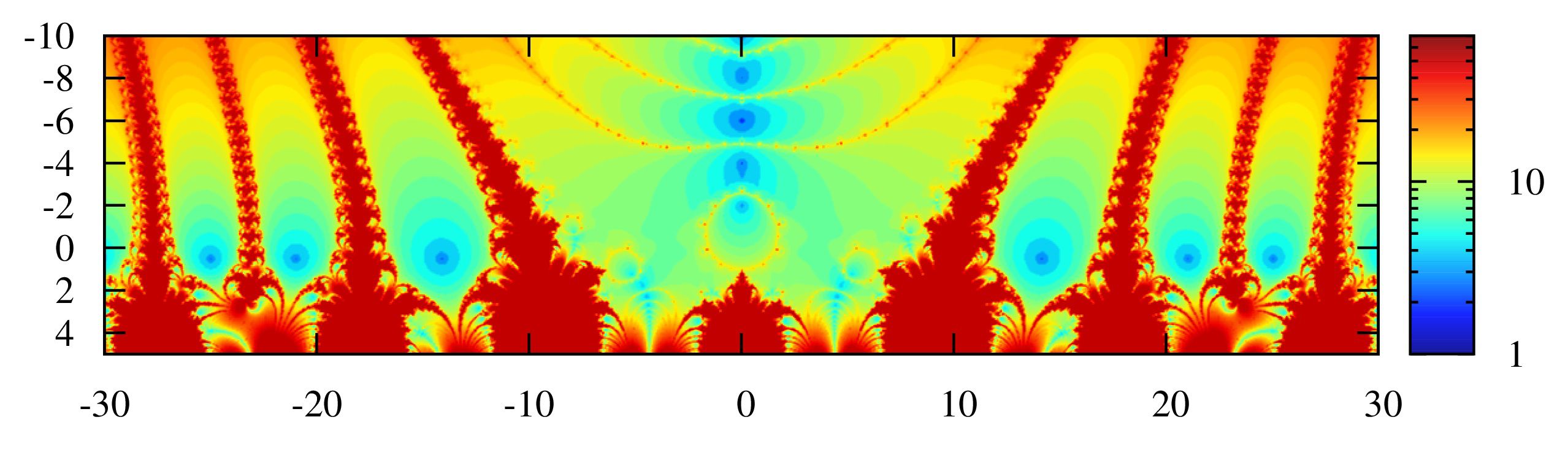
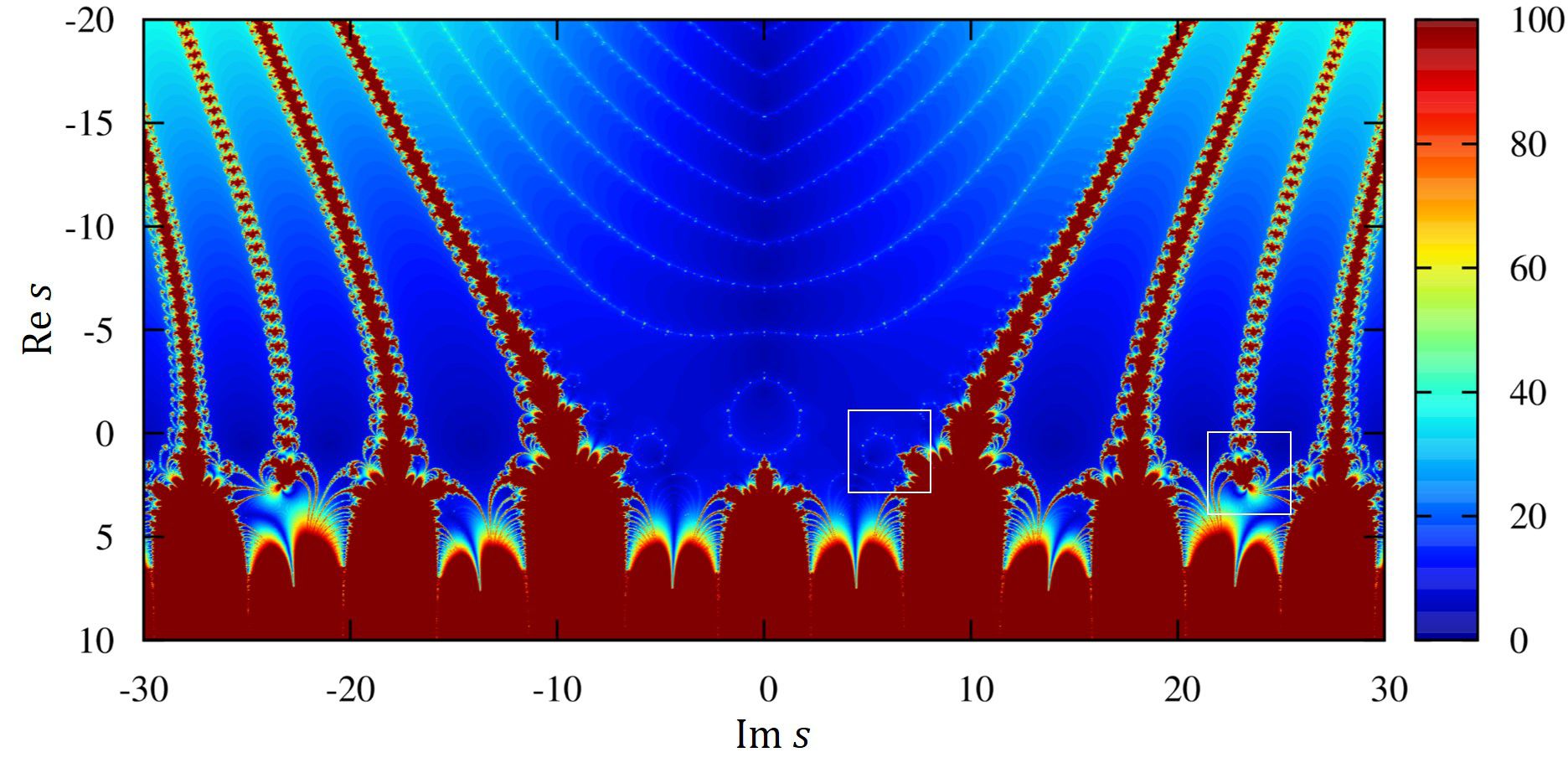
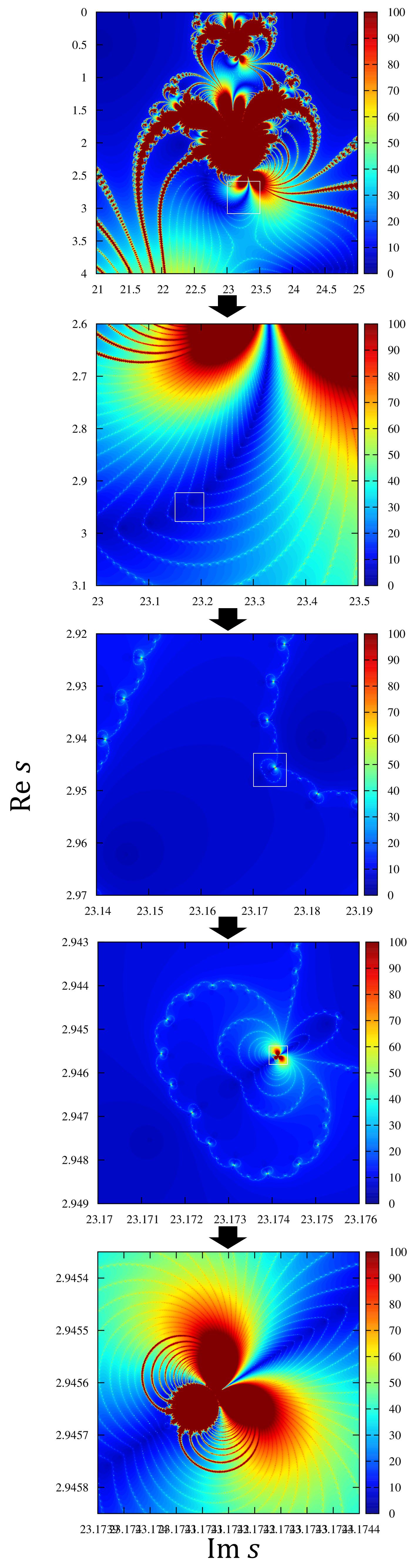
program main
implicit none
integer::i,j,Nx,Ny,prog,omp_get_thread_num
double precision::x,xa,xb,y,ya,yb,hx,hy
integer,allocatable::ns(:,:)
complex(kind(0d0))::czeta,cdzeta
external::czeta,cdzeta
xa=-20d0; xb=20d0
Nx=201
ya=-20d0; yb=20d0
Ny=201
hx=(xb-xa)/dble(Nx-1)
hy=(yb-ya)/dble(Ny-1)
allocate(ns(0:Nx,0:Ny)); ns=0
call omp_set_num_threads(1)
prog=0
!$omp parallel do shared(prog) schedule(dynamic,1)
do i=0,Nx
call tomp(i,Nx,xa,hx,Ny,ya,hy,ns)
prog=prog+1
if(mod(prog,1).eq.0)write(6,'(A,2i6,A,i6)')&
" ",omp_get_thread_num(),prog," / ",Nx
enddo
!$omp end parallel do
do i=0,Nx
x=xa+i*hx
do j=0,Ny
y=ya+j*hy
write(10,*)x,y,ns(i,j)
enddo
write(10,*)
enddo
stop
end program main
subroutine tomp(i,Nx,x0,hx,Ny,y0,hy,ns)
implicit none
integer::i,Nx,Ny
double precision::x0,hx,y0,hy
integer::ns(0:Nx,0:Ny)
integer::j,k,kmax
double precision::x,y,eps
complex(kind(0d0))::z0,z1,czeta,cdzeta,zt,dzt
external::czeta,cdzeta
eps=1d-8
kmax=59
x=x0+i*hx
do j=0,Ny
y=y0+j*hy
z0=dcmplx(x,y)
do k=0,kmax
zt=czeta(z0)
dzt=cdzeta(z0)
z1=z0-zt/dzt
if(abs((z0-z1)/z0).le.eps)exit
z0=z1
enddo
ns(i,j)=k
enddo
return
end subroutine tomp
function czeta(s)
!Checked : ifort (success : version 16.0.2 20160204)
! : gfortran(success : version 4.8.4)
! : gfortran(success : version 4.4.7)
!
!http://slpr.sakura.ne.jp/qp/
! Author : sikino
! date: 2016/06/02, (yyyy/mm/dd)
! : 2016/06/03
! : 2016/06/04
! : 2016/06/05
! : 2016/12/25
! : 2017/01/12
implicit none
complex(kind(0d0)),intent(in)::s
integer,parameter::nmax=100
complex(kind(0d0))::czeta
integer::n,k
double precision::nq,nq1,ln1,ln2
double precision,parameter::eps=1d-15
double precision,parameter::pi=3.14159265358979324d0
complex(kind(0d0))::ds,is,d,s0,tc,tt,qzeta
complex(kind(0d0))::a(0:Nmax),b(0:nmax),cgamma
external::cgamma
ds=dble(s); is=imag(s)
if(ds.eq.1d0.and.is.eq.0d0)then
czeta=1d+300
elseif(ds.eq.0d0.and.is.eq.0d0)then
czeta=-0.5d0
else
if(real(s).lt.1d0)then
s0=1d0-s
else
s0=s
endif
tt=1d0/(1d0-2d0**(1d0-s0))
qzeta=0.5d0*tt
a=cmplx(0d0,0d0,kind=8); b=cmplx(0d0,0d0,kind=8)
b(0)=0.25d0*tt
do n=1,nmax
nq=n
nq1=nq+1d0
a(0)=b(0)
do k=1,n-1
a(k)=b(k)*nq/(n-k)
enddo
!----
ln2=log(nq/nq1)
if(n.eq.1)then
ln1=log(0.5d0)
d=s0*ln1
a(1)=-a(0)*exp(d)/nq
else
d=(ln2/ln1)*d
a(n)=-a(n-1)*exp(d)/nq
ln1=ln2
endif
!----
tc=cmplx(0d0,0d0,kind=8)
do k=0,n
tc=tc+a(k)
enddo
qzeta=qzeta+tc
if(abs(qzeta).ge.1d0)then
if(abs(tc/qzeta).le.eps)exit
else
if(abs(tc).le.eps)exit
endif
b=0.5d0*a
enddo
if(real(s).lt.1d0)then
czeta=(2d0**s)*pi**(-s0)*sin(0.5d0*pi*s)*qzeta*cgamma(s0)
else
czeta=qzeta
endif
end if
return
end function czeta
function cdzeta(s)
!Checked : ifort (success : version 16.0.2 20160204)
! : gfortran(success : version 4.8.4)
!
!http://slpr.sakura.ne.jp/qp/
! Author : sikino
! date: 2016/12/30
! : 2017/01/13
implicit none
complex(kind(0d0)),intent(in)::s
integer,parameter::nmax=100
complex(kind(0d0))::cdzeta
integer::n,k
double precision::nq,nq1,x,y,g1,g2,ds,is
complex(kind(0d0))::d
double precision,parameter::eps=1q-14
double precision,parameter::pi=3.14159265358979324d0
double precision,parameter::ln4=1.386294361119890619d0 ! ln(4)
complex(kind(0d0))::s0,tc,tt,ys,gs,zs,s1,s2,h1,h2
complex(kind(0d0))::a(0:Nmax),b(0:nmax)
complex(kind(0d0))::cgamma
complex(kind(0d0))::czeta,digamma
external::cgamma,czeta,digamma
ds=dble(s); is=imag(s)
if(ds.eq.1d0.and.is.eq.0d0)then
cdzeta=1d+300
elseif(ds.eq.0d0.and.is.eq.0d0)then
cdzeta=-0.5d0*log(2d0*pi)
else
if(real(s).lt.1d0)then
s0=1d0-s
else
s0=s
endif
s1=2d0**s0
s2=s1-2d0
tt=-s1*ln4/(s2*s2)
cdzeta=0.5d0*tt
a=cmplx(0d0,0d0,kind=8); b=cmplx(0d0,0d0,kind=8)
b(0)=cmplx(0.25d0,0d0,kind=8)*tt
do n=1,nmax
nq=n
nq1=nq+1d0
a(0)=b(0)
do k=1,n-1
a(k)=b(k)*nq/(n-k)
enddo
!----
g2=log(nq/nq1)
if(n.eq.1)then
h1=ln4
d=s0*log(0.5d0)
else
d=d*g2/g1
endif
h2=s2*log(nq1)+ln4
a(n)=-a(n-1)*exp(d)*h2/(h1*nq)
g1=g2
h1=h2
!----
tc=cmplx(0d0,0d0,kind=8)
do k=0,n
tc=tc+a(k)
enddo
cdzeta=cdzeta+tc
if(abs(cdzeta).ge.1d0)then
if(abs(tc/cdzeta).le.eps)exit
else
if(abs(tc).le.eps)exit
endif
b=0.5d0*a
enddo
if(real(s).lt.1d0)then
x=-log(2d0*pi)
y=-pi*0.5d0
ys=-y*s0
zs=czeta(1d0-s)
gs=cgamma(s0)
cdzeta=-2d0*(2d0*pi)**(-s0)*(&
(x*cos(ys)+y*sin(ys))*gs*zs+cos(ys)*(digamma(1d0-s)*gs*zs+gs*cdzeta))
else
cdzeta=cdzeta
endif
end if
return
end function cdzeta
function cgamma(z)
! sikinote (http://slpr.sakura.ne.jp/qp)
! author : sikino
! date : 2017/01/09
! 2017/01/10
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::cgamma
integer::i,n,M
double precision,parameter::pi=3.14159265358979324d0
double precision,parameter::e1=0.3678794411714423216d0
double precision,parameter::ln2pi2=0.91893853320467274d0
double precision,parameter::sq2pi=2.5066282746310005d0
double precision::a(1:30),AB(1:14),dz,iz
complex(kind(0d0))::q,s,w,r,q1,q2
dz=dble(z)
iz=imag(z)
if(dz.eq.nint(dz).and.iz.eq.0d0)then
if(dz.gt.0d0)then
s=dcmplx(1d0,0d0)
n=nint(dz)
do i=2,n
s=s*i
enddo
else
s=1d+300
endif
cgamma=s
else
q=z
if(dz.lt.0d0)q=1d0-z
if(abs(iz).lt.1.45d0)then
! For x=arb, |y|\lt 1.45
n=int(dble(q))
s=1d0
do i=1,n
s=s*(q-i)
enddo
w=q-dble(n)
a(1) = 1d0
a(2) = 0.57721566490153286d0
a(3) =-0.65587807152025388d0
a(4) =-0.42002635034095236d-1
a(5) = 0.16653861138229149d0
a(6) =-0.42197734555544337d-1
a(7) =-0.96219715278769736d-2
a(8) = 0.72189432466630995d-2
a(9) =-0.11651675918590651d-2
a(10)=-0.21524167411495097d-3
a(11)= 0.12805028238811619d-3
a(12)=-0.20134854780788239d-4
a(13)=-0.12504934821426707d-5
a(14)= 0.11330272319816959d-5
a(15)=-0.20563384169776071d-6
a(16)= 0.61160951044814158d-8
a(17)= 0.50020076444692229d-8
a(18)=-0.11812745704870201d-8
a(19)= 0.10434267116911005d-9
a(20)= 0.77822634399050713d-11
a(21)=-0.36968056186422057d-11
a(22)= 0.51003702874544760d-12
a(23)=-0.20583260535665068d-13
a(24)=-0.53481225394230180d-14
a(25)= 0.12267786282382608d-14
a(26)=-0.11812593016974588d-15
a(27)= 0.11866922547516003d-17
a(28)= 0.14123806553180318d-17
a(29)=-0.22987456844353702d-18
a(30)= 0.17144063219273374d-19
M=int(11.3*abs(w)+13)
if(M.gt.30)M=30
r=a(M)
do i=M-1,1,-1
r=r*w+a(i)
enddo
cgamma=s/(r*w)
else
! For x=arb, |y|\gt 1.45
s=1d0
if(abs(q).lt.9d0)then
do i=0,7
s=s*(q+i)
enddo
s=1d0/s
q=q+8d0
endif
AB(1) = 0.83333333333333333d-1
AB(2) =-0.27777777777777778d-2
AB(3) = 0.79365079365079365d-3
AB(4) =-0.59523809523809524d-3
AB(5) = 0.84175084175084175d-3
AB(6) =-0.19175269175269175d-2
AB(7) = 0.64102564102564103d-2
AB(8) =-0.29550653594771242d-1
q1=1d0/q
q2=q1*q1
r=AB(8)
do i=7,1,-1
r=r*q2+AB(i)
enddo
cgamma=s*exp((q-0.5d0)*log(q)-q+ln2pi2+r*q1)
endif
if(dz.lt.0d0)cgamma=pi/(cgamma*sin(pi*z))
endif
return
end function cgamma
function digamma(z)
! digamma function for complex plane
! sikinote, http://slpr.sakura.ne.jp/qp/
! author : sikino
! date : 2016/07/04 (yyyy/mm/dd)
! date : 2016/07/07 (yyyy/mm/dd)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::digamma
integer::i,n,m,as,key
integer,parameter::nmax=50
double precision::eps=1d-13
double precision::pi=4d0*atan(1d0)
complex(kind(0d0))::w,ds,s
double precision::B
external::B
as=10
if(dble(z).ge.dble(as))then
w=z
key=0
elseif(dble(z).ge.1d0)then
w=z+dble(as)
key=1
elseif(dble(z).ge.-dble(as-1))then
w=1d0-z+dble(as)
key=2
else
w=1d0-z
key=3
endif
! Asymptotic expansion
s=log(w)-0.5d0/w
do n=1,nmax
m=2*n
ds=B(m)/(m*w**m)
s=s-ds
if(abs(ds)/abs(s).le.eps)exit
enddo
if(n.eq.nmax+1)then
write(6,*)"Worning! did not converge at digamma"
endif
if(key.eq.1.or.key.eq.2)then
!Recurrence relation
do i=1,as
s=s+1d0/(1d0-w)
w=w-1d0
enddo
endif
if(key.eq.2.or.key.eq.3)then
! Reflection Formula
s=s-pi/tan(pi*z)
endif
digamma=s
return
end function digamma
!--------------------------
function B(n)
! 1st bernoulli number B(n), 0 <= n <= 100
! from wolfram alpha
! " Table[bernoulli b(i), {i,0,100}] with 17 digits "
implicit none
integer,intent(in)::n
double precision::B
double precision::A(0:100)
if(n.lt.0.or.n.gt.100)then
write(6,*)"Not expected n at bernoulli number function. "
write(6,*)"program stop"
stop
endif
A(0:100)=(/1d0 &
, -0.50000000000000000d0, 0.16666666666666667d0, 0d0, -0.033333333333333333d0, 0d0 &
, 0.023809523809523810d0, 0d0, -0.033333333333333333d0, 0d0, 0.075757575757575758d0, 0d0 &
, -0.25311355311355311d0, 0d0, 1.1666666666666667d0, 0d0, -7.0921568627450980d0, 0d0 &
, 54.971177944862155d0, 0d0, -529.12424242424242d0, 0d0, 6192.1231884057971d0, 0d0 &
, -86580.253113553114d0, 0d0, 1.4255171666666667d+6, 0d0, -2.7298231067816092d+7, 0d0 &
, 6.0158087390064237d+8, 0d0, -1.5116315767092157d+10, 0d0, 4.2961464306116667d+11, 0d0 &
, -1.3711655205088333d+13, 0d0, 4.8833231897359317d+14, 0d0, -1.9296579341940068d+16, 0d0 &
, 8.4169304757368262d+17, 0d0, -4.0338071854059455d+19, 0d0, 2.1150748638081992d+21, 0d0 &
, -1.2086626522296526d+23, 0d0, 7.5008667460769644d+24, 0d0, -5.0387781014810689d+26, 0d0 &
, 3.6528776484818123d+28, 0d0, -2.8498769302450882d+30, 0d0, 2.3865427499683628d+32, 0d0 &
, -2.1399949257225334d+34, 0d0, 2.0500975723478098d+36, 0d0, -2.0938005911346378d+38, 0d0 &
, 2.2752696488463516d+40, 0d0, -2.6257710286239576d+42, 0d0, 3.2125082102718033d+44, 0d0 &
, -4.1598278166794711d+46, 0d0, 5.6920695482035280d+48, 0d0, -8.2183629419784576d+50, 0d0 &
, 1.2502904327166993d+53, 0d0, -2.0015583233248370d+55, 0d0, 3.3674982915364374d+57, 0d0 &
, -5.9470970503135448d+59, 0d0, 1.1011910323627978d+62, 0d0, -2.1355259545253501d+64, 0d0 &
, 4.3328896986641192d+66, 0d0, -9.1885528241669328d+68, 0d0, 2.0346896776329074d+71, 0d0 &
, -4.7003833958035731d+73, 0d0, 1.1318043445484249d+76, 0d0, -2.8382249570693707d+78/)
B=A(n)
return
end function B