phase unwrapping

phase unwrappingという処理があります。
これは、振動関数から位相を抽出しよう、ということを実現する処理です。
具体的に問題を書けば、関数
\(\displaystyle
y(x)=\sin(\phi(x))
\)
があり、\(y(x)\)だけが分かっているときに、\(\phi(x)\)を求める、という問題です。
仮定として、\(\phi(x)\)は滑らかな関数であるとします。

逆関数を作用させれば良いということはすぐに思いつきます。つまり、\(\sin\)の逆関数である\(\sin^{-1}\)を作用させればよく、
\(\displaystyle
\begin{align}
\sin^{-1}y(x)&=\sin^{-1}\sin(\phi(x)) \\
&=\phi(x)
\end{align}
\)
を期待します。

しかしながら、ここで問題が生じます。
それは、\(\sin^{-1}(x)\)の値域は\([-\pi/2,\pi/2]\)ですので、この範囲に押し込まれてしまうということです。

もし\(\phi(x)\)が\([-\pi/2,\pi/2]\)の範囲以外にはない、という仮定があるならば話は別ですが、
通常は\(\phi(x)=[-\infty, \infty]\)ですので、\(\sin^{-1}(x)\)を作用させた場合、値域の端で位相に不連続が生じることになります。
つまり、ただ単に\(\sin^{-1}\)を作用させただけでは、\(\phi(x)\)が滑らかである、という条件に矛盾することになります。

しかしながら、\(\sin^{-1}\sin(\phi(x))\)と\(\phi(x)\)は全く無関係なもの、というわけではありません。
\(
\begin{align}
\sin(\theta)&=-\sin(-\theta) \\
\sin(\theta)&=\sin(\theta+2n\pi), ~~~(n=0,\pm 1,\pm 2,\cdots)
\end{align}
\)
の性質があるため、\(\sin^{-1}\cos(\phi(x))\)の角度を負に取ったり、適当に\(2n\pi\)を足したり引いたりすれば、どこかに元の\(\phi(x)\)と一致する組み合わせが見つかるはずです。

このように、関数の自由度を一つに決めて、制限された関数の値域を元に戻すことをunwrappingと言います。
位相の場合は特にphase unwrappingと呼ばれます。

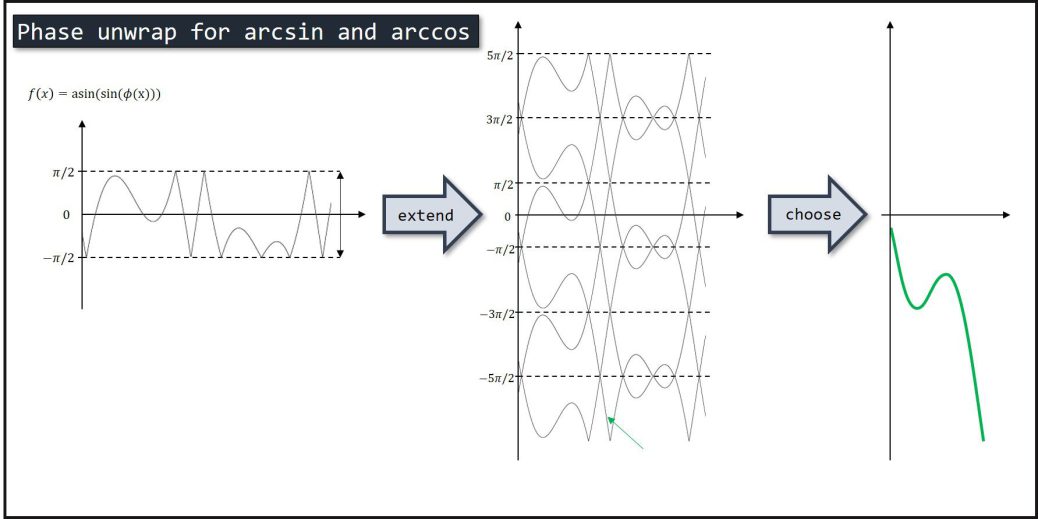
先にどのようなことを考えるか図示してみます。
入力は下の図の黒線で、ここから赤線を復元できるか？という問題です。

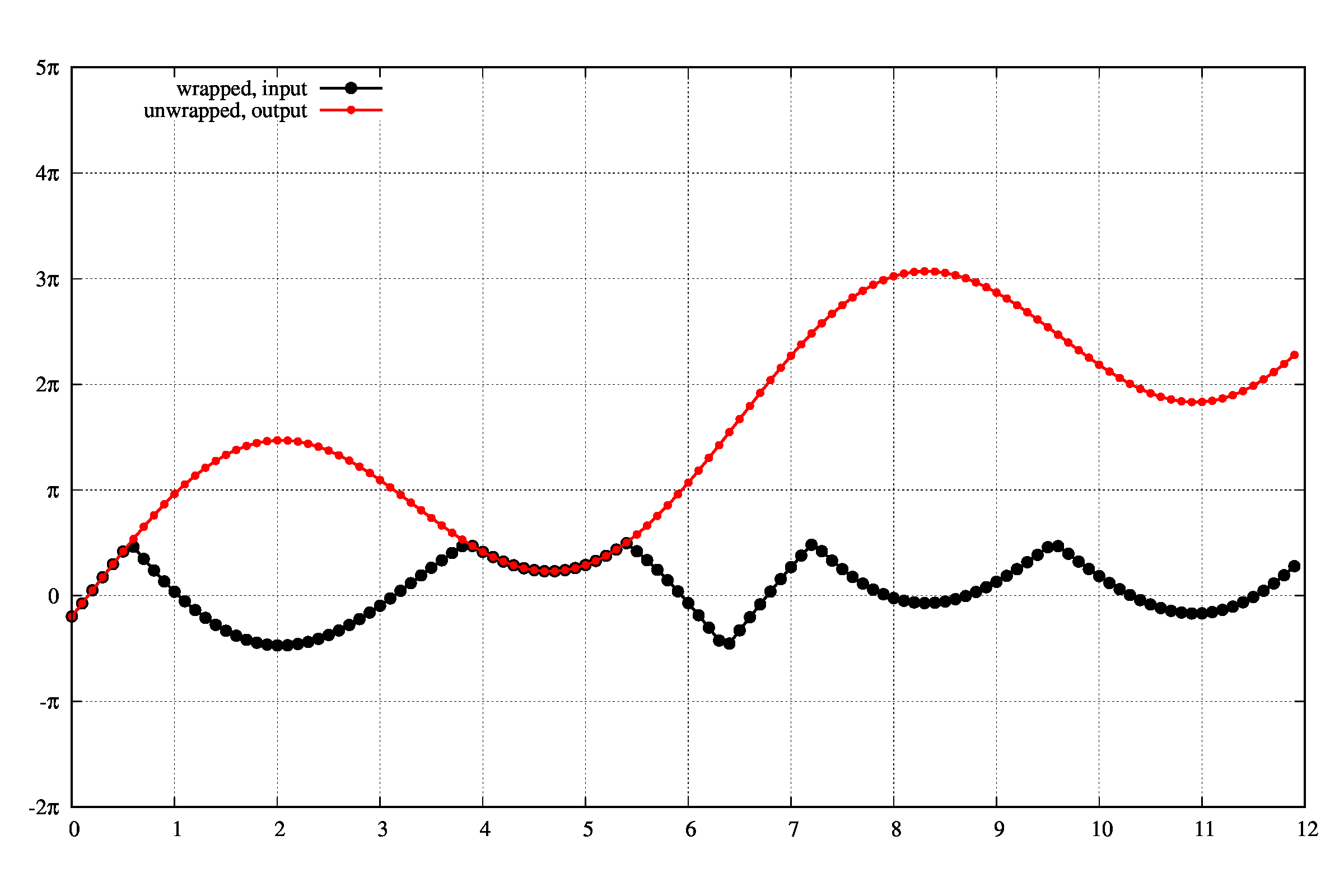
どのように\(\phi(x)\)と一致する組み合わせ見つけるかは様々な方法が考えられますが、愚直な方法で実装しましょう。
ここでは一例として、\(\phi(x)\)は滑らかである場合を考えて、補外によってphase unwrappingを行う方法を実装してみます。

方針

滑らかに接続できたことを考えたとしても、絶対的な位相の量は分からないので、適当な\(x_0\)における位相の値\(\sin^{-1}\sin(\phi(x_0))\)を基準として、その位置から滑らかにつながることを想定します。

以下の仮定の下で考えます。

• 離散的な\(y(x_n)=\sin^{-1}\sin(\phi(x_n)), (n=1,2,\cdots,N)\)が等間隔で与えられている。
• 入力\(y(x_n)\)の値域は\([0,\pi]\)または\([-\pi/2,\pi/2]\)
• \(\phi(x)\)は滑らかであること
• \(\phi(x)\)が局所的には2次程度の多項式で書けること

まず、基準点より一つ進んだ点の候補(\(\sin(\theta)=-\sin(-\theta), \sin(\theta)=\sin(\theta+2n\pi)\)の関係から考えられるもの)を挙げ、その中から期待されるであろう補外の値に最も近い点がunwrappingされた点だ、と考えます。

unwrapされる候補の点を挙げる

左側の元の関数\(y(x_n)\)から、右のように候補を生成します。候補は、これまでにunwrapされた関数を値の周辺のみを候補とします。

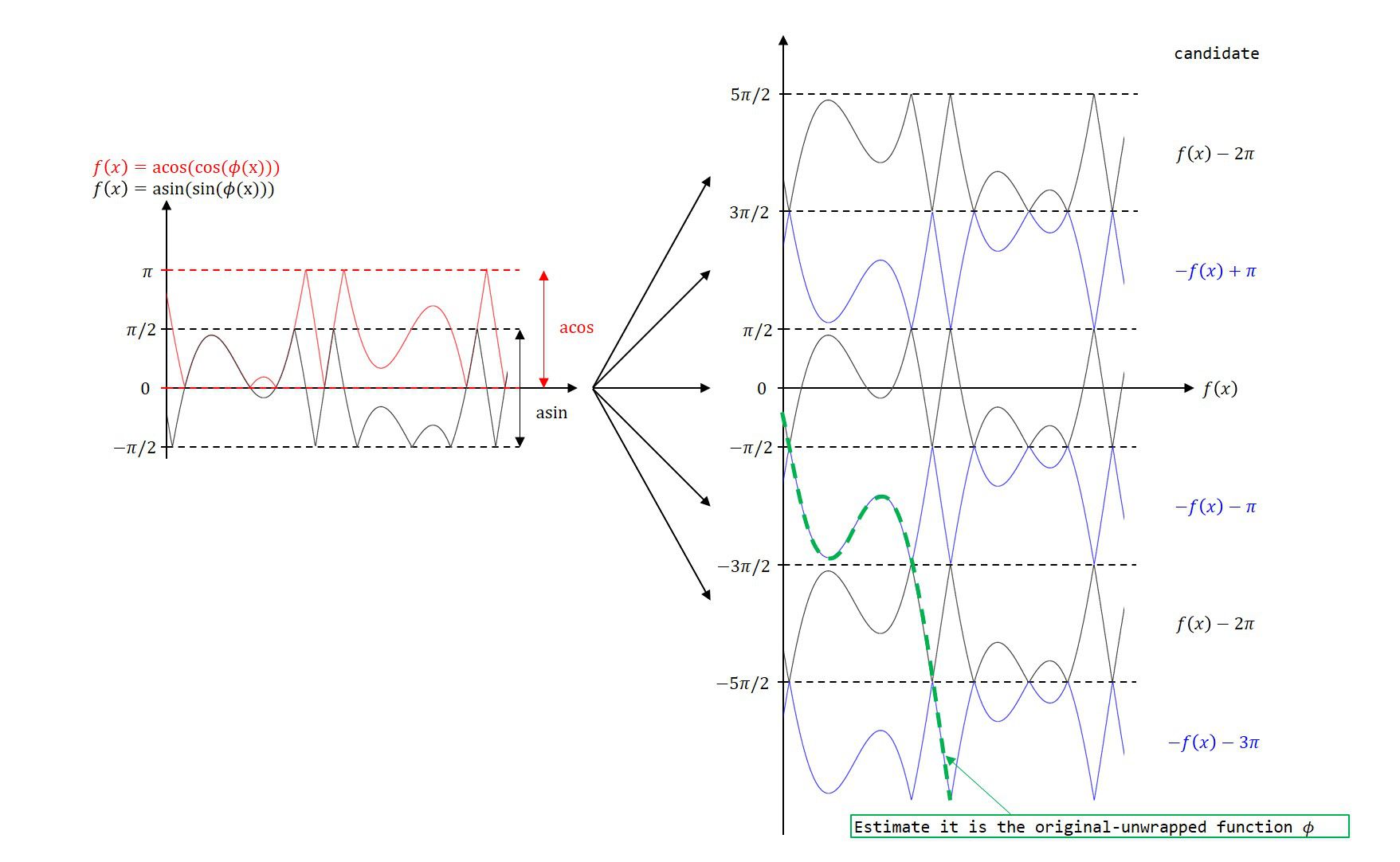
補外と上手くいかない場合

基本的なアイデアは下図左側で、これまでにunwrapされた点を元に次の点を予測し、それに最も近い候補点がunwrapの値とします。この補外によって、\([-\pi/2,\pi/2]\)ないし\([0,\pi]\)から\([-\infty, \infty]\)の領域に拡張できます。

また、異なる候補と接近する境界付近では間違えて予測する可能性があります。それは右のような状況です。
これは補外が正しく行われないことが理由なので、逆向きにも次の点を予測し、その平均を取ることで精度が上がることを期待します。

コード

Fortran90のコードです。

失敗する場合

離散した点と点の間隔が広い場合

本アルゴリズムの場合、どうしても境界付近で曲がる場合、別の領域のものをトレースしてしまう可能性があります。
厳密に傾きがゼロになり、候補が複数ある場合に正解を選び出すのは不可能です。本アルゴリズムの適用を諦めましょう。
しかしながら、元のデータ点を補間なり何かをしてマシにすることはできますので、データ点を増やして再度実行すると成功するかもしれません。

具体的に例を挙げてみます。

関数
\(\displaystyle
\begin{align}
y(x)&=acos(cos(\phi(x))) \\
& phi(x)=3.1cos(2*x)**2+exp(-0.2x)-0.8
\end{align}
\)
を考えます（適当に試していた時に失敗した関数なので、これより単純な関数でも細かく離散化されていなければ失敗するはずです）。

離散化する間隔\(\Delta x\)を\(\Delta x=0.1\)でとり、unwrapすると失敗します。

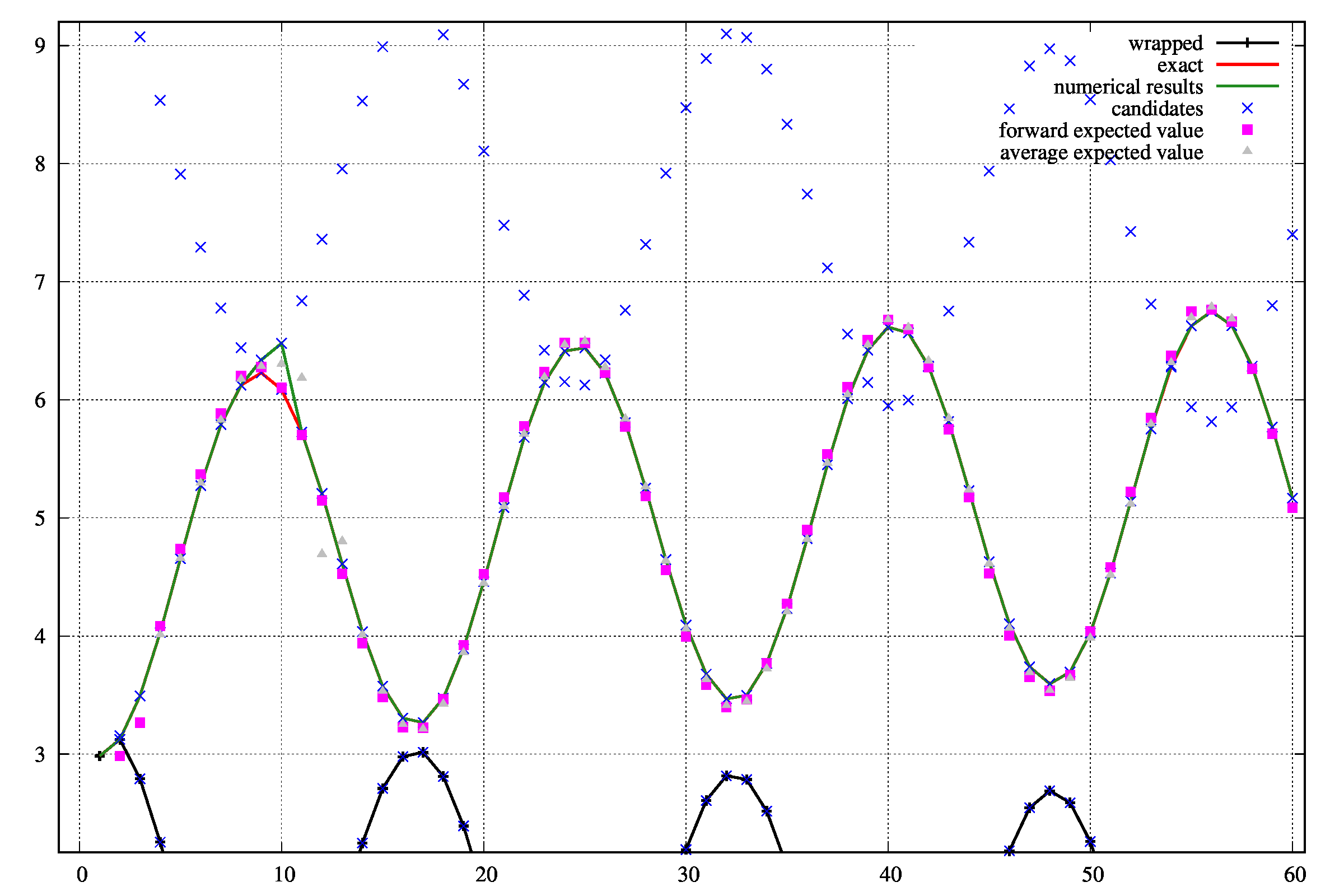
上図の横軸は離散点のインデックス、縦軸は候補やその他の情報を示しています。\(cos(x)\)の任意性は無視しています。
数値的な解は緑線であり、9,10番目の離散点（\(x=0.9, 1.0\)）で失敗しており、本来の解（赤線）とは異なる点を結んでしまっています。

しかしながら、離散化する間隔\(\Delta x\)を\(\Delta x=0.05\)でとり、unwrapすると成功します。

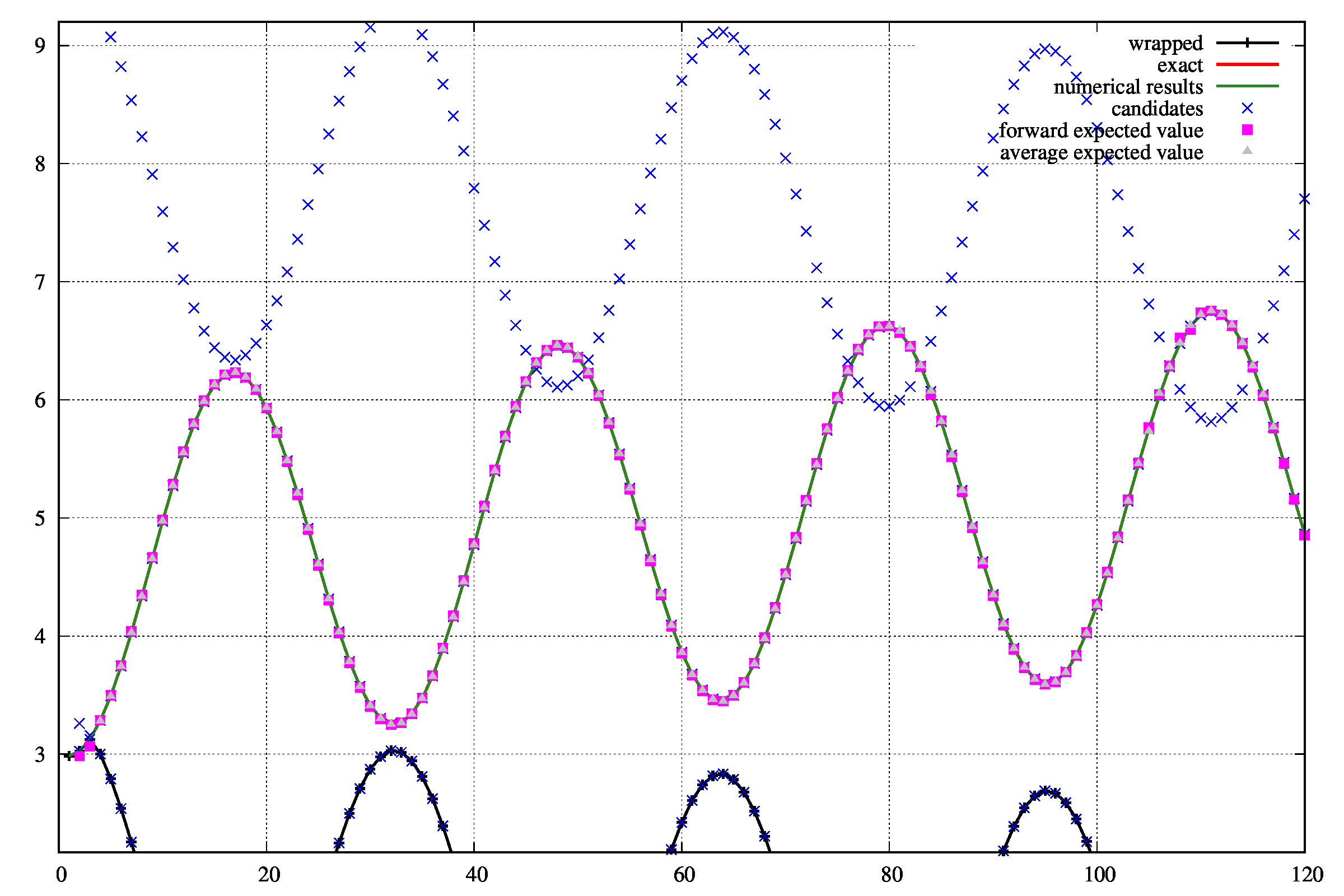
成功させるためには、できるだけ細かい間隔で離散化しましょう。

Tweet