数値計算での積分方法、特に等間隔の分点の場合であるニュートン・コーツ積分(とロンバーグ積分)に関する理論とのプログラムを載せます。
- ニュートンコーツ型の公式
- ルンゲ現象
- ロンバーグ積分
- サブルーチン”integral”のコードと使い方
- サブルーチン”romberg”のコードと使い方
等間隔の分点で積分を行う場合、よく使われる方法は台形則、もしくはシンプソン積分です。
台形則
台形則は、分点間を台形近似して面積を求める方法であり、下図のようなイメージで積分を近似する方法です。
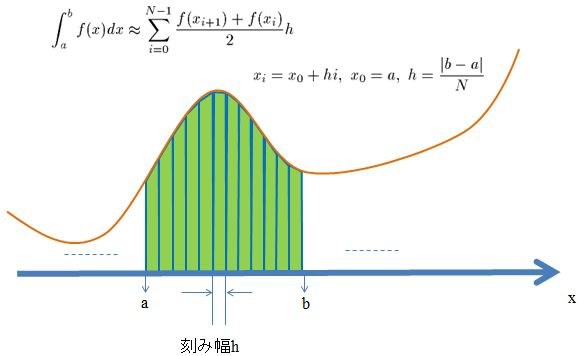
積分\(\displaystyle \int_a^b f(x) dx\)を、
\(
\displaystyle \int_a^b f(x) dx \sim \sum_{i=0}^{N-1} \frac{f(x_{i+1})+f(x_i)}{2}h
\)
として近似します。この時、誤差のオーダーは\(O(h^3)\)となります。
言い換えると、
台形積分とは、隣り合う分点間を1次関数で近似して求める積分
言えます。
シンプソン積分
シンプソン積分は、隣り合う分点間を2次関数で近似して求める積分です。イメージは
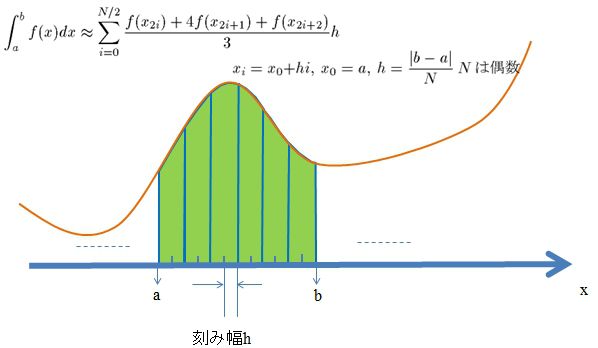
な感じです。数式では
\(
\displaystyle \int_a^b f(x) dx \sim \sum_{i=0}^{N/2} \frac{f(x_{2i})+4f(x_{2i+1})+f(x_{2i+2})}{3}h
\)
となります。
高次≠高精度
これ以降もあります。分点間を3次、4次、…としていけば高次の積分をすることが可能になります。
この分点間の次数をどんどん上げていって積分をする方法をまとめてニュートンコーツの公式、と呼びます。
例えばの台形則はニュートンコーツの公式の1次に相当し、シンプソン則はニュートンコーツの公式の2次に相当しています。
じゃあ100次の公式作れば精度が凄い公式ができるんじゃないか?となりますが、これは違います。
高次であることと精度が高いことは違うのです。だから使うな、というわけではなくて知っておいてほしいことなんです。
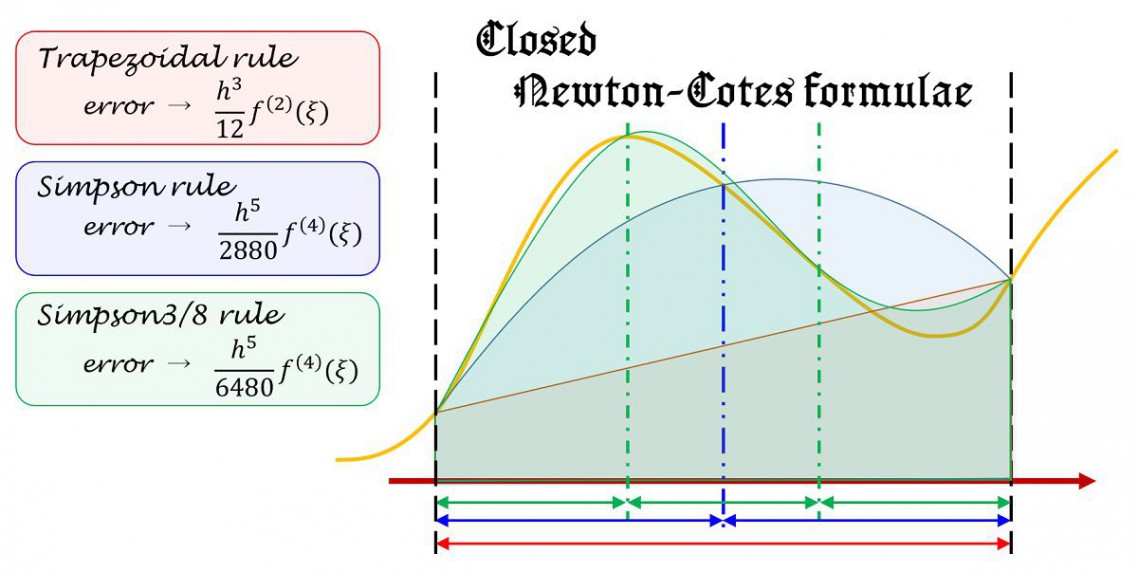
ではなぜか?これはwikipediaのニュートンコーツの公式のページからとってきたものですが、この式に理由があります。

問題となるのが誤差項です。例えば台形近似を見ますと、誤差項は\(h^3 f^{(2)}(\xi)\)とあります。hは刻み幅なので、この項は刻み幅を小さくすれば小さくするほど精度がよくなることを言っています。
が、問題は\(f^{(2)}(\xi)\)の方です。この項は本当の関数が分からないと評価できません。
多項式だったら微分するごとに次数が1つづつ減少するのでこの項は高次になれば小さくなります。じゃあもしも微分するごとに値が増加していったら…?この場合、hを小さくしてもそれを上回るくらい\(f^{(2)}(\xi)\)が大きくなることがあります。これをルンゲ現象と呼びます。
ルンゲ現象
例えば関数
\(
\displaystyle f(x)=\frac{1}{1+25x^2}
\)
を考えます。wikipediaのページを参考にすれば、その導関数と値は、

となります。高次になればなるほど値が増加する関数なのです。
実際には\(h^n f^{(m)}(\xi)\)の積の値が小さいか大きいか?なので、一概には高次は悪い!とは言えません。高次は危ないくらいでしょう。
これを可能な限り回避するために、低次の積分を組み合わせて使う方法がとられます。
こうすることで高次の値を増加を抑えるのです。
そのほかの手法もいろいろあります。分点の位置に縛られなければガウス求積法が最高でしょう。素晴らしい方法です。ぜひ調べてみてください。
[adsense1]
ロンバーグ積分
さて、高次を追い求めるのもいいですが、一線を駕す…とまではいきませんが、ロンバーグ(Romberg)積分というものがあります。
このロンバーグ積分とは、台形則による計算を基本とし、無限小区間での積分結果を補外によって求めよう、というものです。
ここでいう補外の概念は以下のような感じです。
刻み幅1で台形則の結果から積分値S1が分かる
↓
刻み幅0.5で台形則による結果から積分値S2がわかる
↓
刻み幅0.25で台形則による結果から積分値S3がわかる
↓
刻み幅0.175で台形則による結果から積分値S4がわかる
とある程度計算していきます。そうすると刻み幅hを変化させるとそれに応じて積分値がS1→S2→S3→S4…と推移していくわけです。
この推移の仕方を計算すれば、刻み幅無限小の場合の積分値Sが分かる、こういう仕組みになっています。収束加速法と言ったり、リチャードソン補外、なんて言ったりします。
この補外による方法はかなり優れています。先ほどの高次がどうこう、といった問題が発生しないのです。台形則しか使ってないんですから。有限桁計算に適した方法である、とかwikipediaに載ってたりします。
ロンバーグ積分の詳しい計算方法や理論は
ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ
を見ると詳しく書かれています。
日本語では第6章 数値積分と数値微分にロンバーグ積分の記述があります。
英語ではRomberg integralで調べると良いでしょう。参考までに、英語では
Romberg integration exampleや、Romberg Integrationなにかがいいと思います。
2016/03/01
上のRomberg Integrationを参考にして書いたプログラムはこちらです。これは、解析関数fをRomberg積分するプログラムです。
解析関数ではなく、サイズ\(2^{n}+1\)の配列に格納されている場合はこのページの下の方にあるプログラムを参照してください。
で呼び出し、区間a~bの積分\(s=\int_a^b f(x) dx\)を精度preで求めるプログラムです。
サブルーチン”integral”のコードと使い方
下のサブルーチン”integral”は1,2,3次元の短冊近似、台形則、シンプソン積分、シンプソン3/8積分、ブール則(ニュートン・コーツ型積分)をカバーします。
ただし、分点の個数に注意してください。分点の個数を気にせず使える近似方法は、短冊近似、台形近似のみです。
ロンバーグ積分では引数の関係上、ニュートン・コーツ型積分との間をうまく処理できなかったため、別のサブルーチンとして書きます。もしもロンバーグ積分を使いたい場合はもう少し先に進んでください。
まずはニュートン・コーツ型積分です。
下のサブルーチンを使ってください。
使い方は、
という感じです。
実際のプログラムでは、以下のように使用してください。配列yは複素数解列(ただし実軸上の積分)でもokです。
1次元
| 積分則 | 呼び方 | |
|---|---|---|
| 短冊近似(長方形近似) |
call integral(size(w,1),w,h,s,"box") |
配列yの大きさに指定はない。 |
| 台形近似 |
call integral(size(y,1),y,h,s,"trapezoid") |
配列yの大きさに指定はない。 |
| シンプソン則 |
call integral(size(y,1),y,h,s,"simpson") |
配列yの大きさが3,5,7,…個、\(2n+1\)個でないといけない |
| シンプソン3/8則 |
call integral(size(y,1),y,h,s,"simpson38") |
配列yの大きさが4,7,10,…個、\(3n+1\)個でないといけない |
| ブール則 |
call integral(size(y,1),y,h,s,"boole") |
配列yの大きさが5,9,13,…個、\(4n+1\)個でないといけない |
2次元配列の場合は以下のように指定してください。
|
call integral(size(w,1),size(w,2),w,hx,hy,s,"simpson") |
3次元の場合はこう指定してください。
|
call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"simpson") |
積分のためのモジュール
!developer --> sikino
!date --> 2015/04/07
implicit none
interface integral
module procedure &
dintegral, &
dintegral2d, &
dintegral3d, &
cintegral, &
cintegral2d, &
cintegral3d
end interface integral
contains
subroutine dintegral(N,y,h,s,method)
integer,intent(in)::N
double precision,intent(in)::h,y(1:N)
character(*),intent(in)::method
double precision,intent(out)::s
integer::i
double precision::y0,y1,y2,y3
s=0.d0; y0=0.d0; y1=0.d0; y2=0.d0; y3=0.d0
if(trim(method).eq."box")then
s=h*sum(y(1:N-1))
elseif(trim(method).eq."trapezoid")then
y1=y(1)+y(N)
do i=2,N-1
y2=y2+y(i)
enddo
s=(y1+2.d0*y2)*h*0.5d0
elseif(trim(method).eq."simpson")then
if(mod(N,2).ne.1)then
write(6,*)"=====cannot calculation with simpson"
write(6,*)"=====program stop"
stop
endif
y1=y(1)+y(N)
do i=2,N-1,2
y2=y2+y(i)
enddo
do i=3,N-2,2
y3=y3+y(i)
enddo
s=(y1+4.d0*y2+2.d0*y3)*h/3.d0
elseif(trim(method).eq."simpson38")then
if(mod(N,3).ne.1)then
write(6,*)"=====cannot calculation with simpson38"
write(6,*)"=====program stop"
stop
endif
y0=y(1)+y(N)
do i=2,N-2,3
y1=y1+y(i)
enddo
do i=3,N-1,3
y2=y2+y(i)
enddo
do i=4,N-3,3
y3=y3+y(i)
enddo
s=(y0+3.d0*(y1+y2)+2.d0*y3)*3.d0*h/8.d0
elseif(trim(method).eq."boole")then
if(mod(N,4).ne.1)then
write(6,*)"=====cannot calculation with boole"
write(6,*)"=====program stop"
stop
endif
y0=y(1)+y(N)
do i=5,N-4,4
y1=y1+y(i)
enddo
do i=2,N-1,2
y2=y2+y(i)
enddo
do i=3,N-2,4
y3=y3+y(i)
enddo
s=(14.d0*y0+28.d0*y1+64.d0*y2+24.d0*y3)*h/45.d0
else
write(6,*)"=====cannot calculation in integral"
write(6,*)"=====program stop"
stop
end if
return
end subroutine dintegral
subroutine dintegral2d(Nx,Ny,z,hx,hy,s,method)
implicit none
integer,intent(in)::Nx,Ny
double precision,intent(in)::hx,hy,z(1:Nx,1:Ny)
character(*),intent(in)::method
double precision,intent(out)::s
integer::i
double precision::ty(1:Ny),r(1:Nx)
s=0.d0
ty(1:Ny)=0.d0
r(1:Nx)=0.d0
do i=1,Nx
ty(1:Ny)=z(i,1:Ny)
call integral(Ny,ty,hy,s,method)
r(i)=s
enddo
call integral(Nx,r,hx,s,method)
return
end subroutine dintegral2d
subroutine dintegral3d(Nx,Ny,Nz,w,hx,hy,hz,s,method)
implicit none
integer,intent(in)::Nx,Ny,Nz
double precision,intent(in)::hx,hy,hz,w(1:Nx,1:Ny,1:Nz)
character(*),intent(in)::method
double precision,intent(out)::s
integer::i
double precision::tyz(1:Ny,1:Nz),r(1:Nx)
s=0.d0
tyz(1:Ny,1:Nz)=0.d0
r(1:Nx)=0.d0
do i=1,Nx
tyz(1:Ny,1:Nz)=w(i,1:Ny,1:Nz)
call integral(Ny,Nz,tyz,hy,hz,s,method)
r(i)=s
enddo
call integral(Nx,r,hx,s,method)
return
end subroutine dintegral3d
subroutine cintegral(N,y,h,s,method)
integer,intent(in)::N
complex(kind(0d0)),intent(in)::y(1:N)
double precision,intent(in)::h
character(*),intent(in)::method
complex(kind(0d0)),intent(out)::s
double precision::res,ims
s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0
call integral(N,dble(y),h,res,trim(method))
call integral(N,dimag(y),h,ims,trim(method))
s=dcmplx(res,ims)
return
end subroutine cintegral
subroutine cintegral2d(Nx,Ny,z,hx,hy,s,method)
integer,intent(in)::Nx,Ny
complex(kind(0d0)),intent(in)::z(1:Nx,1:Ny)
double precision,intent(in)::hx,hy
character(*),intent(in)::method
complex(kind(0d0)),intent(out)::s
double precision::res,ims
s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0
call integral(Nx,Ny,dble(z),hx,hy,res,trim(method))
call integral(Nx,Ny,dimag(z),hx,hy,ims,trim(method))
s=dcmplx(res,ims)
return
end subroutine cintegral2d
subroutine cintegral3d(Nx,Ny,Nz,w,hx,hy,hz,s,method)
integer,intent(in)::Nx,Ny,Nz
complex(kind(0d0)),intent(in)::w(1:Nx,1:Ny,1:Nz)
double precision,intent(in)::hx,hy,hz
character(*),intent(in)::method
complex(kind(0d0)),intent(out)::s
double precision::res,ims
s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0
call integral(Nx,Ny,Nz,dble(w),hx,hy,hz,res,trim(method))
call integral(Nx,Ny,Nz,dimag(w),hx,hy,hz,ims,trim(method))
s=dcmplx(res,ims)
return
end subroutine cintegral3d
end module integral_mod
サブルーチン”integral”を用いた例題
実際の使い方。参考にどうぞ。
下のコードは2次元の積分
\(
\displaystyle \int\int xe^{-x^2}e^{-y}dxdy=\frac{e^{-x^2}}{2}e^{-y}+\mbox{const}
\)
を数値積分します。積分範囲を\(x=0\sim 3, \; y=0 \sim 5\)にした場合、その解析解は
\(
\begin{align}
\int_0^3 dx\int_0^5 dy xe^{-x^2}e^{-y}&=\frac{1}{2}(1-e^{-5}-e^{-9}+e^{-14})\\
&=0.4965697373627734784608751894356320535936864348993604\cdots
\end{align}
\)
となります。実行すると
simpson : 0.496569737366759E+000
romberg,3 : 0.496569737362773E+000
となります。コードは、
use integral_mod
implicit none
integer::i,j,n,Nx,Ny
double precision::hx,hy,ans
double precision::xmin,xmax,ymin,ymax
double precision,allocatable::x(:),y(:)
double precision::s
double precision,allocatable::w(:,:)
double precision::f
external::f
n=10
xmin=0d0
xmax=3d0
ymin=0d0
ymax=5d0
Nx=2**(n)
Ny=2**(n)
allocate(x(0:Nx),y(0:Ny),w(0:Nx,0:Ny))
x=0d0; y=0d0; w=dcmplx(0d0,0d0)
hx=(xmax-xmin)/dble(Nx)
hy=(ymax-ymin)/dble(Ny)
do i=0,Nx
x(i)=xmin+hx*dble(i)
enddo
do i=0,Ny
y(i)=ymin+hy*dble(i)
enddo
do i=0,Nx
do j=0,Ny
w(i,j)=f(x(i),y(j))
end do
end do
call integral(size(w,1),size(w,2),w,hx,hy,s,"simpson")
write(6,'(A,e25.15e3)')"simpson : ",s
call integral(size(w,1),size(w,2),w,hx,hy,s,"romberg",3)
write(6,'(A,e25.15e3)')"romberg,3 : ",s
return
end program main
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
f=x*exp(-x*x)*exp(-y)
return
end function f
3次元の計算の例題です。
下のコードは
\(
\displaystyle \int\int\int x^4y^4z^4 dxdydz=\left(\frac{1}{5}\{0.7^5-(-1)^5\}\right)^3
\)
を数値積分します。積分範囲を\(x,y,z=-1\sim 0.7\)にした場合、その値は
\(
\displaystyle \int_{-1}^{0.7}\int_{-1}^{0.7}\int_{-1}^{0.7} x^4y^4z^4 dxdydz = 0.127496010896795\cdots
\)
となります。実行すると、
$ ./a.out
analysis : 0.127496010896795E-01
simpson : 0.10507613E-006 0.10507613E-006
romberg,3 : -0.17347235E-017 -0.17347235E-017
と得られます。中身はこうです。分点の数はx,y,z軸各々で違っていて構いません。
use integral_mod
implicit none
integer::i,j,k,n,Nx,Ny,Nz
double precision::hx,hy,hz,ans
double precision,allocatable::x(:),y(:),z(:)
complex(kind(0d0))::s
complex(kind(0d0)),allocatable::w(:,:,:)
n=6
Nx=2**(n)
Ny=2**(n-1)
Nz=2**(n+1)
allocate(x(0:Nx),y(0:Ny),z(0:Nz),w(0:Nx,0:Ny,0:Nz))
x=0d0; y=0d0; z=0d0; w=dcmplx(0d0,0d0)
hx=1.7d0/dble(size(w,1)-1)
hy=1.7d0/dble(size(w,2)-1)
hz=1.7d0/dble(size(w,3)-1)
do i=0,Nx
x(i)=hx*dble(i)-1d0
enddo
do i=0,Ny
y(i)=hy*dble(i)-1d0
enddo
do i=0,Nz
z(i)=hz*dble(i)-1d0
enddo
do i=0,Nx
do j=0,Ny
do k=0,Nz
w(i,j,k)=dcmplx((x(i)*y(j)*z(k))**4,(x(i)*y(j)*z(k))**4)
end do
end do
end do
ans=(0.7d0**5.d0+1.d0)/5.d0
ans=ans**3.d0
write(6,'(A,e23.15e2)')"analysis : ",ans
call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"simpson")
write(6,'(A,2e17.8e3)')"simpson : ",dble(s)-ans,dimag(s)-ans
call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"romberg",3)
write(6,'(A,2e17.8e3)')"romberg,3 : ",dble(s)-ans,dimag(s)-ans
return
end program main
ロンバーグ積分のプログラム
| ロンバーグ積分 |
call romberg(jx,x,y,s,pre) |
配列yの大きさは2,3,5,10,…,\(2^{jx}+1\)個でないといけない | ロンバーグ積分では収束精度”pre”を指定すること。もしも収束精度に達しなかった場合、警告と共に、与えられた値での収束限界の積分結果を返す。積分精度を高めたければ刻み幅を小さくする操作(例えば分点数を増やす等)をしてください。”pre”は、積分結果の絶対値が1より大きくなる場合は相対誤差を、小さくなる場合は絶対誤差を取ります。この理由は以前の結果の補正を加え、収束をさせるためであり、非常に小さい誤差の場合いつまでたっても機械誤差のため収束しないからです。 |
!developer --> sikino
!date --> 2016/03/01
! 2016/03/03
!
! 1D case :
! romberg(jx,x,y,s,pre)
! | | | | +- (in) precision (e.g. 1d-8)
! | | | +--- (out) integration result
! | | +----- (in) y(1:2**jx+1) f(x)
! | +------- (in) x(1:2**jx+1) x
! +---------- (in) related to array size
!
! 2D case :
! romberg(jx,jy,x,y,z,s,pre)
! | | | | | | +-- (in) precision (e.g. 1d-8)
! | | | | | +---- (out) integration result
! | | | | +------ (in) z(1:2**jx+1,1:2**jy+1) f(x,y)
! | | | +-------- (in) y(1:2**jy+1) y
! | | +---------- (in) x(1:2**jx+1) x
! | +------------- (in) related to array size y
! +---------------- (in) related to array size x
!
! 3D case :
! romberg(jx,jy,jz,x,y,z,w,s,pre)
! | | | | | | | | +-- (in) precision (e.g. 1d-8)
! | | | | | | | +---- (out) integration result
! | | | | | | +------ (in) w(1:2**jx+1,1:2**jy+1,1:2**jz+1) f(x,y,z)
! | | | | | +-------- (in) z(1:2**jz+1) z
! | | | | +---------- (in) y(1:2**jy+1) y
! | | | +------------ (in) x(1:2**jx+1) x
! | | +--------------- (in) related to array size z
! | +------------------ (in) related to array size y
! +--------------------- (in) related to array size x
!
implicit none
interface romberg
module procedure &
dromberg, &
dromberg2d, &
dromberg3d
end interface romberg
contains
subroutine dromberg(jx,x,y,s,pre)
implicit none
integer,intent(in)::jx
double precision,intent(in)::x(1:2**jx+1),y(1:2**jx+1),pre
double precision,intent(out)::s
integer,parameter::jm=6 !--> precision: O(h^(2*jm))
integer,parameter::nm=2**jm
double precision,allocatable::tx(:),ty(:)
double precision::ts
integer::k
s=0d0
if(jx.ge.jm)then
allocate(tx(1:nm+1),ty(1:nm+1)); tx=0d0; ty=0d0
do k=0,2**(jx-jm)-1
ts=0d0
tx(1:nm+1)=x(k*nm+1:(k+1)*nm+1)
ty(1:nm+1)=y(k*nm+1:(k+1)*nm+1)
call romberg_sub(jm,tx,ty,ts,pre)
s=s+ts
enddo
deallocate(tx,ty)
else
call romberg_sub(jx,x,y,s,pre)
endif
return
end subroutine dromberg
subroutine romberg_sub(jx,x,y,s,pre)
! reference "http://www.math.usm.edu/lambers/mat460/fall09/lecture29.pdf"
implicit none
integer,intent(in)::jx
double precision,intent(in)::x(1:2**jx+1),y(1:2**jx+1),pre
double precision,intent(out)::s
integer::i,j,k,n,dn
double precision::h,ps,tmp
double precision::T(1:jx+1,1:jx+1)
n=2**jx+1
h=x(n)-x(1)
dn=(n-1)/2
T(1,1)=0.5d0*h*(y(1)+y(n))
s=T(1,1)
ps=s
h=0.5d0*h
do j=2,jx+1
! trapezoidal rule
tmp=0d0
do i=1,2**(j-2)
tmp=tmp+y(1+(2*i-1)*(dn))
enddo
T(j,1)=0.5d0*T(j-1,1)+h*tmp
do k=2,j
! Richardson extrapolation
T(j,k)=T(j,k-1)+(T(j,k-1)-T(j-1,k-1))/(dble(4**(k-1))-1d0)
enddo
s=T(j,j)
! precision check
if(abs(s).ge.1d0)then
if(abs((ps-s)/s).le.pre)exit
else
if(abs((ps-s)).le.pre)exit
endif
ps=s
h=0.5d0*h
dn=dn/2
enddo
if(j-1.eq.jx)then
write(6,'(A)')" -+-+- didn't converge at romberg integral -+-+- "
write(6,'(A)')" Please change stepsize h of array x "
endif
return
end subroutine romberg_sub
subroutine dromberg2d(jx,jy,x,y,z,s,pre)
implicit none
integer,intent(in)::jx,jy
double precision,intent(in)::pre,x(1:2**jx+1),y(1:2**jy+1)
double precision,intent(in)::z(1:2**jx+1,1:2**jy+1)
double precision,intent(out)::s
integer::i,nx,ny
double precision::ty(1:2**jy+1),r(1:2**jx+1)
nx=2**jx+1
ny=2**jy+1
s=0.d0
ty(1:ny)=0.d0
r(1:nx)=0.d0
do i=1,nx
ty(1:ny)=z(i,1:ny)
call romberg(jy,y,ty,s,pre)
r(i)=s
enddo
call romberg(jx,x,r,s,pre)
return
end subroutine dromberg2d
subroutine dromberg3d(jx,jy,jz,x,y,z,w,s,pre)
implicit none
integer,intent(in)::jx,jy,jz
double precision,intent(in)::pre,x(1:2**jx+1),y(1:2**jy+1),z(1:2**jz+1)
double precision,intent(in)::w(1:2**jx+1,1:2**jy+1,1:2**jz+1)
double precision,intent(out)::s
integer::i,nx,ny,nz
double precision::tyz(1:2**jy+1,1:2**jz+1),r(1:2**jx+1)
nx=2**jx+1; ny=2**jy+1; nz=2**jz+1
s=0.d0
tyz(1:ny,1:nz)=0.d0
r(1:nx)=0.d0
do i=1,nx
tyz(1:ny,1:nz)=w(i,1:ny,1:nz)
call romberg(jy,jz,y,z,tyz,s,pre)
r(i)=s
enddo
call romberg(jx,x,r,s,pre)
return
end subroutine dromberg3d
end module romberg_mod
ロンバーグ積分(romberg_mod)の例
必要なのは、上で紹介したモジュール “romberg_mod” と下のメインプログラムです。
以下のプログラムは1次元の定積分
\(
\int_1^10 \frac{1}{x^2} dx = 0.9
\)
を分点数\(2^8+1(jx=8)\)個でロンバーグ積分するものです。
精度は\(O(h^{2\cdot min{jm,jx}})\)です。
ここで\(jm\)はモジュールromberg_modの中にパラメータとして宣言されています。
コンパイルは
とでもすればいいでしょう。
use romberg_mod
implicit none
integer::i,jx,n
double precision::h,a,b,s
double precision,allocatable::x(:),y(:)
double precision::f
external::f
a=1d0
b=10d0
jx=8
n=2**jx+1
allocate(x(1:n),y(1:n))
h=(b-a)/dble(n-1)
do i=1,n
x(i)=a+h*dble(i-1)
y(i)=f(x(i))
enddo
call romberg(jx,x,y,s,1d-8)
write(6,*)s,"romberg"
stop
end program main
function f(x)
implicit none
double precision::f,x
f=1d0/(x*x)
return
end function f
実行例(要求精度は\(10^{-8}\))
0.900000000062642
>
2次元ではこう。
use romberg_mod
implicit none
integer::i,j,Nx,Ny,jx,jy
double precision::hx,hy
double precision::xmin,xmax,ymin,ymax
double precision,allocatable::x(:),y(:)
double precision::s
double precision,allocatable::w(:,:)
double precision::f
external::f
jx=10
jy=8
xmin=0d0
xmax=3d0
ymin=0d0
ymax=5d0
Nx=2**(jx)
Ny=2**(jy)
allocate(x(0:Nx),y(0:Ny),w(0:Nx,0:Ny))
x=0d0; y=0d0; w=dcmplx(0d0,0d0)
hx=(xmax-xmin)/dble(Nx)
hy=(ymax-ymin)/dble(Ny)
do i=0,Nx
x(i)=xmin+hx*dble(i)
enddo
do i=0,Ny
y(i)=ymin+hy*dble(i)
enddo
do i=0,Nx
do j=0,Ny
w(i,j)=f(x(i),y(j))
end do
end do
call romberg(jx,jy,x,y,w,s,1d-8)
write(6,*)s
stop
end program main
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
f=x*exp(-x*x)*exp(-y)
return
end function f
実行例
0.496569737374163
>
[adsense2]