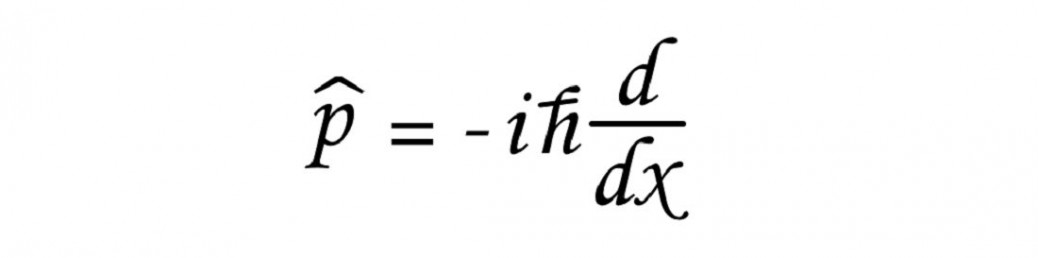量子力学の運動量演算子\(\hat{p}\)が
\(
\displaystyle \hat{p}=-i\hbar \frac{d}{d x}
\)
であらわされることを導出します。
ここでの”導出”は運動量演算子として妥当なものを導出する、と言った方がいいかもしれません。

平行移動演算子\(\hat{T}\)を出発点とします。
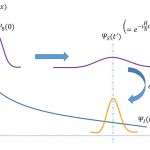
この平行移動演算子はある波動関数\(\psi_{(x)}\)を平行移動させる演算子で、これを作用させると
\(
\hat{T}_{(\Delta x)}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
となる演算子です。

よく説明される、シュレディンガー方程式の平面波解からの出発はしません。

この\(\hat{T}\)の持つであろう性質を考え、その特性から\(\hat{T}\)の具体的な形を推定し、運動量演算子を導きます。

平行移動演算子\(\hat{T}\)が満たすべき性質

---

当たり前と思われる性質から、平行移動演算子に関して以下の4つが言えます。

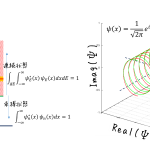
1. 波動関数\(\psi_{(x)}\)が1に規格化済みであれば、平行移動した波動関数\(\psi_{(x+\Delta x)}\)もまた規格化されているはずである。
   すなわち、
   \(
   \begin{align}
   \langle\psi_{(x)}|\psi_{(x)}\rangle &= \langle\psi_{(x)}|\hat{T}^{\dagger}_{(\Delta x)}\hat{T}_{(\Delta x)}|\psi_{(x)}\rangle \\
   &= \langle\psi_{(x+\Delta x)}|\psi_{(x+\Delta x)}\rangle \\
   &\rightarrow \hat{T}^{\dagger}_{(\Delta x)}\hat{T}_{(\Delta x)}=\mathbf{1}
   \end{align}
   \)
   となり、3本目の式から\(\hat{T}\)はユニタリー演算子であることがわかります。
2. \(\Delta x\)進めた後、\(\Delta x^{\prime}\)を進める操作は\(\Delta x + \Delta x^{\prime}\)進める操作に等しいはずである。
   すなわち、
   \(
   \hat{T}_{(\Delta x^{\prime})}\hat{T}_{(\Delta x)}=\hat{T}_{(\Delta x+\Delta x^{\prime})}
   \)
3. 負の方向への平行移動\(\hat{T}_{(-\Delta x)}\)は正の方向への平行移動\(\hat{T}_{(\Delta x)}\)の逆のはずである。
   \(
   \hat{T}_{(-\Delta x)}=\hat{T}^{-1}_{(\Delta x)}
   \)
4. \(\Delta x\)が0のとき、恒等操作なはずである。
   \(
   \begin{align}
   \hat{T}_{(0)}\psi_{(x)}&=\psi_{(x)} \\
   &\rightarrow \hat{T}_{(0)}=\mathbf{1}
   \end{align}
   \)

平行移動演算子の具体的な形

---

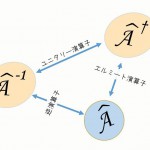
1,より、\(\hat{T}_{(\Delta x)}\)はユニタリー演算子である事が分かりました。ユニタリー演算子を作る1つの方法として、エルミート演算子\(\hat{A}_{(\Delta x)}\)を用いて、
\(
\hat{T}_{(\Delta x)}=e^{i\hat{A}_{(\Delta x)}}
\)
と置けば、\(\hat{T}_{(\Delta x)}\)はユニタリー演算子となります(エルミート演算子とユニタリー演算子の性質)。
この仮定の下、
\(
\hat{T}_{(\Delta x)}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
に代入して、
\(
e^{i\hat{A}_{(\Delta x)}}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
無限小移動を考えて\(\Delta_{(x)}\rightarrow 0\)と約束すれば、
\(
(1+i\hat{A}_{(\Delta x)})\psi_{(x)}=\psi_{(x+\Delta x)}
\)
変形して、
\(
\psi_{(x+\Delta x)}-\psi_{(x)}=i\hat{A}_{(\Delta x)}\psi_{(x)}
\)
辺々を\(\Delta x\)で割れば、
\(
\begin{align}
\displaystyle \lim_{\Delta x\rightarrow 0}\frac{\psi_{(x+\Delta x)}-\psi_{(x)}}{\Delta x} = \lim_{\Delta x\rightarrow 0} i\frac{\hat{A}_{(\Delta x)}}{\Delta x}\psi_{(x)}
\end{align}…(i)
\)
となります。左辺は位置\(x\)における波動関数の傾きです。
ここで右辺を見ます。\(\hat{A}_{(\Delta x)}\)は\(\Delta x\)のなんらかの関数であるはずですが、\(\hat{A}_{(\Delta x)}\)が分母の\(\Delta x\)と打ち消す形でなければ0、もしくは発散する事になります。
この場合、波動関数の傾きが到る点で0になるということは、全空間で定数ということになり非物理的な解です。また、発散してしまうのであれば波動関数が至る所で発散してしまい、これまた日物理的です。

具体的に、もしも\(\hat{A}_{(\Delta x)}=(\Delta x)^2\)だったら、
\(
\displaystyle \lim_{\Delta x\rightarrow 0} \frac{(\Delta x)^2}{\Delta x}=\lim_{\Delta x\rightarrow 0} \Delta x =0
\)
であるし、もしも\(\hat{A}_{(\Delta x)}=(\Delta x)^{1/2}\)だったら
\(
\displaystyle \lim_{\Delta x\rightarrow 0} \frac{(\Delta x)^{1/2}}{\Delta x}=\lim_{\Delta x\rightarrow 0} \frac{1}{\sqrt{\Delta x}} =\infty
\)
となります。
すなわち、言いたいことは、\(\hat{A}_{(\Delta x)}\)は\(\Delta x\)に関して1次であるべきで、
\(
\hat{A}_{(\Delta x)}=\hat{B}\cdot \Delta x
\)…(ii)
と書けるはずです。ここで\(\hat{B}\)は\(\Delta x\)に依らない演算子です(下に補足説明あり)。

よって、式(i)は\(\Delta x\rightarrow 0\)のとき、
\(
\begin{align}
\displaystyle \lim_{\Delta x\rightarrow 0}\frac{\psi_{(x+\Delta x)}-\psi_{(x)}}{\Delta x} &= \lim_{\Delta x\rightarrow 0} i\frac{\hat{A}_{(\Delta x)}}{\Delta x}\psi_{(x)} \\
\frac{d \psi_{(x)}}{dx}=i\hat{B}\psi_{(x)}
\end{align}…(iii)
\)
と書けるため、
\(
\psi_{(x)}=e^{i\hat{B}\cdot x}\psi_{(0)}
\)
となります。(この式で右辺の\(\psi_{(0)}\)が0である必要はなく、定数であればいいんです。)

平行移動演算子と運動量演算子との関係

---

次元について考えましょう！
今、\(\hat{T}_{(\Delta x)}=e^{i\hat{B}\cdot \Delta x}\)であり、\(\Delta x\)の次元は\(\mathrm{[m]}\)であるため、\(\hat{B}\)の次元は\(\mathrm{[m^{-1}]}\)でなければなりません。よって、\(\hat{B}\)は波数の次元を持つ演算子であると考えられるため、\(\hat{B}\)を\(c\hat{k}\)と記述することにします。ここで、\(c\)は無次元の定数です。
式(iii)より、
\(
\displaystyle \frac{d \psi_{(x)}}{dx}=ic\hat{k}\psi_{(x)}
\)
辺々に\(-i\hbar\)を掛けると、
\(
\displaystyle -i\hbar \frac{d}{dx} \psi_{(x)}=c\hbar \hat{k}\psi_{(x)}
\)…(iv)

!!!

\(p=\hbar k\)は運動量を表すものでした。よって,\(\hat{p}=\hbar \hat{k}\)と書けば、式(iv)より
\(
\begin{align}
\hat{p}\psi_{(x)}&=\frac{1}{c}\left[-i\hbar\frac{d}{d x}\right] \psi_{(x)} \\
\end{align}
\)
となります。よって運動量演算子は
\(
\begin{align}
\hat{p}\propto -i\hbar\frac{d}{d x} \\
\end{align}
\)
となります。この考えからは定数倍を含めてしまうので、比例する、という事しか言えません。

なぜ決まらないのか考えてみますと、時間の依存性に関する考え方が式のどこにも含んでいないからです。
時間の単位が決まらないと速度の定義が出来ないわけで、これ以上進めることが出来ないのです。

各成分について言えるので、多次元の場合では
\(
\hat{p}_x\propto -i\hbar\frac{\partial}{\partial x}
\)
としても同じことです。
申し訳ないですが、数学的に厳密か？は保証しません。

補足説明

---

果たして運動量演算子として考えた\(e^{i\hat{B}\cdot \Delta x}\)は\(\hat{T}\)の特性1.~4.を満たすでしょうか？

1. \(
   \left(e^{i\hat{B}\cdot \Delta x}\right)^{\dagger} \left(e^{i\hat{B}\cdot \Delta x}\right)=e^{-i\hat{B}^{\dagger}\cdot \Delta x}e^{i\hat{B}\cdot \Delta x}=\mathbf{1}
   \)
   ここで\(\hat{B}\)はエルミート演算子を考えているので、\(\hat{B}^{\dagger}=\hat{B}\)です。
   \(
   e^{-i\hat{B}^{\dagger}\cdot \Delta x}e^{i\hat{B}\cdot \Delta x}=\mathbf{1}
   \)
   ok!
2. \(
   \hat{T}_{(\Delta x^{\prime})}\hat{T}_{(\Delta x)}=\hat{T}_{(\Delta x+\Delta x^{\prime})}
   \)か？
   \(
   (\mbox{左辺})=e^{i\hat{B}\cdot \Delta x^{\prime}} e^{i\hat{B}\cdot \Delta x}=e^{i\hat{B}\cdot (\Delta x^{\prime}+\Delta x)}
   \)
   ok!
3. \(
   \hat{T}_{(-\Delta x)}=\hat{T}^{-1}_{(\Delta x)}
   \)か？
   両辺の左から\(\hat{T}_(\Delta x)\)を掛けて、
   \(
   \begin{align}
   &\hat{T}_{(\Delta x)}\hat{T}_{(-\Delta x)}=\mathbf{1} \\
   &= e^{i\hat{B}\cdot \Delta x}e^{i\hat{B}\cdot (-\Delta x)}=e^{i\hat{B}\cdot 0}=\mathbf{1}
   \end{align}
   \)
   ok!
4. \(e^{i\hat{B}\cdot 0}=1\)
   ok!

よって、4つすべてを満たすので、\(\hat{T}_{(\Delta x)}=e^{i\hat{B}\cdot \Delta x}\)は平行移動演算子として適当であると考えることができるのです。