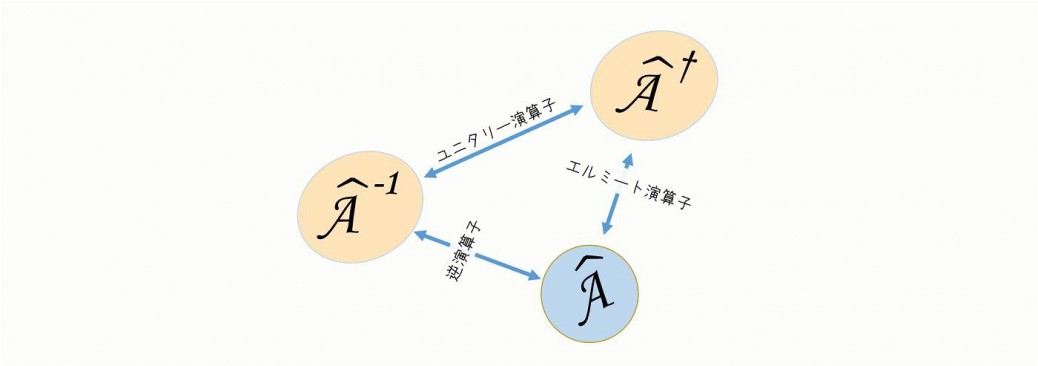
\(\hat{A}\)がエルミート演算子ならば、\(e^{i\hat{A}}\)はユニタリー演算子である。

この文の意味が分かる人はこのページはいらないと思います。

---

前提として、一度勉強した人が思い出す、という体を想定しています。
詳しくブラケット表記であるとか、正しく知りたい人は、
J. J. Sakurai著 桜井 明夫訳『現代の量子力学〈上〉』 (物理学叢書) (1989)

や
David J.Tannor著 山下晃一訳 『入門 量子ダイナミクス 時間依存の量子力学を中心に（上）』 化学同人
などを参考にしてください。このページの参考先もこの２つです。

[adsense1]

エルミート演算子(Hermite Operator)

---

エルミート演算子は自己随伴演算子とも呼ばれます。

• ディラックのブラ・ケット表記で考えます。
  演算子\(\hat{A}\)の状態\(u\)と状態vによる内積を\(\langle u|\hat{A}|v\rangle \)と、表現します。
  関数による表現では、
  \(
  \displaystyle \langle u|\hat{A}|v\rangle =\int u^* \hat{A} v dx
  \)
  となるわけです。この時、
  \(
  \langle u|\hat{A}|v\rangle^*=\langle v|\hat{A}^{\dagger}|u\rangle
  \)
  を関係を満たす演算子を随伴演算子と呼び、\(\hat{A}^{\dagger}\)と表現します(\(\hat{A}\)のエルミート共役を取る、とも言います)。

  状態による表記では、
  \(
  \displaystyle \hat{A}|v\rangle =\lambda |v\rangle
  \)
  に対してエルミート共役を取ると、
  \(
  \displaystyle \langle v|\hat{A}^{\dagger} =\lambda^* \langle v|
  \)
  と書けます。

  そして、たまたま\(\hat{A}^{\dagger}\)が\(\hat{A}\)に等しい場合、すなわち、
  \(
  \hat{A}^{\dagger}=\hat{A}
  \)
  を満たすとき、演算子\(\hat{A}\)はエルミート演算子(自己随伴演算子)だ、と呼びます。

• エルミート演算子の持つ性質

  1. エルミート演算子の固有値は実数である。
     \(
     \hat{A}|v\rangle=\lambda |v\rangle
     \)
     左から\(v\)を掛けて、内積を取り、式変形します。式変形は２通り考えられて、
     
     \(
     \begin{eqnarray}
     \left\{
     \begin{aligned}
     \langle v|\hat{A}|v\rangle&=\langle v|\lambda |v\rangle=\lambda\langle v|v\rangle \\
     \langle v|\hat{A}|v\rangle&=\langle v|\hat{A}^{\dagger}|v\rangle=
     \langle v|\lambda^*|v\rangle=\lambda^*\langle v|v\rangle
     \end{aligned}
     \right .
     \end{eqnarray}
     \)

     となります。同じものから出発したので値は同じものになるはずです。なので
     \(\lambda=\lambda^*\)
     これを満たす\(\lambda\)は虚数部がゼロでなければなりません。
     よってエルミート演算子の固有値は実数である、となります。

  2. あるエルミート演算子が異なる2つの固有値を持つ場合、これらの固有値に対応する固有関数は互いに直交する。
     ２つの固有値を\(\lambda_1, \lambda_2\)と書いて、
     それぞれの固有値に属する固有ベクトルを\(|v_1\rangle, |v_2\rangle\)と書くことにします。すなわち、
     \(
     \hat{A}|v_1\rangle=\lambda_1 |v_1\rangle \ ,\ \ \ \ \hat{A}|v_2\rangle=\lambda_2 |v_2\rangle
     \)
     であるとします。ここで\(\lambda_1\neq \lambda_2\)です。
     1番目の式に左から左から\(\langle v_2|\)を作用させて式変形します。式変形は２通り考えられて、
     \(
     \begin{eqnarray}
     \left\{
     \begin{aligned}
     \langle v_2|\hat{A} |v_1\rangle&=\langle v_2|\lambda|v_1\rangle=\lambda_1\langle v_2|v_1\rangle \\
     \langle v_2|\hat{A}|v_1\rangle&=\langle v_2|\hat{A}^{\dagger}|v_1\rangle=
     \lambda_2^*\langle v_2|v_1\rangle=\lambda_2\langle v_2|v_1\rangle
     \end{aligned}
     \right .
     \end{eqnarray}
     \)
     同じものから出発したので、
     \(
     \begin{align}
     \lambda_1\langle v_2|v_1\rangle=\lambda_2\langle v_2|v_1\rangle \\
     \rightarrow (\lambda_1-\lambda_2)\langle v_2|v_1\rangle=0
     \end{align}
     \)
     仮定より、\(\lambda_1\neq \lambda_2\)なので、\(\langle v_2|v_1\rangle=0\)になるほかありません。
     \(\langle v_2|v_1\rangle=0\)は内積がゼロ、すなわち直交である、と言っているので仮定は示されました。

ある状態\(\phi\)が、演算子\(A\)の固有値\(\lambda_i\)に属する固有状態\({v_i}\)の組で書かれるとき、
すなわち、
\(
\displaystyle |\phi\rangle=\sum_ia_i|v_i\rangle
\)
で書かれるとき、
\(
\displaystyle \frac{\langle\phi|\hat{A}|\phi\rangle}{\langle\phi|\phi\rangle}
=\sum_i p_i \lambda_i,\ \ \ p_i\equiv \frac{|a_i|^2}{\sum_i|a_i|^2}\ \ \cdots (a)
\)

• 量子力学の中心的教義は以下の3つを主張しています。
  (i)     全ての観測量にはエルミート演算子\(\hat{A}\)が結び付けられる。
  (ii)   \(\hat{A}\)に属する観測量の測定について、起こりうる結果は\(A\)の固有値\(\{A_i\}\)のみ。
  (iii)  系が状態\(|\phi\rangle=\sum_ia_i|v_i\rangle\)にあれば、
  \(\lambda_i\)の値を得る確率は\((a)\)で与えた\(p_i\)で与えられる。
  また、\(\displaystyle \sum_ip_i\lambda_i\)は\(\hat{A}\)を測定した平均値、もしくは期待値である。
• おまけ
  随伴行列\(A^{\dagger}\)は、\(\hat{A}\)の転置行列の複素共役で与えられます。
  \(
  (A_{ij})^{\dagger}=A^*_{ji}
  \)
  特に、エルミート行列の場合、\(A^{\dagger}=A^*\)なので、
  \(
  A_{ij}=A^*_{ji}
  \)
  対角要素については\(A_{ii}=A^*_{ii}\)が成り立つので、エルミート行列の対角要素は実数でなければならないことがわかります。

逆演算子

---

\(\hat{A}\)の逆\(\hat{A}^{-1}\)を意味します。

• 定義

  \(\hat{A}|u\rangle=|v\rangle\ \ \ \cdots (1)\)
  のとき、逆演算子\(\hat{A}^{-1}\)は
  \(|u\rangle=\hat{A}^{-1}|v\rangle\ \ \ \cdots (2)\)
  と定義されます。

• 性質

  (1)の左から\(\hat{A}^{-1}\)を作用させると、
  \(\hat{A}^{-1}\hat{A}|u\rangle=\hat{A}^{-1}|v\rangle\ \ \ \cdots (1-1)\)
  (2)の左から\(\hat{A}\)を作用させると、
  \(\hat{A}\hat{A}^{-1}|u\rangle=\hat{A}|v\rangle\ \ \ \cdots (2-1)\)

  (1)と(2-1), (2)と(1-1)を見比べれば、明らかに
  \(\hat{A}\hat{A}^{-1}=\hat{A}^{-1}\hat{A}=\mathbf{1}\)
  となります。

• 逆演算子の存在
  全ての演算子に逆演算子があるわけではありません。以下の通り、逆が存在しない場合があることを示せます。
  演算子\(\hat{A}\)が2つの異なる初期ベクトルを同じ終ベクトルに写す状況を考えます。式で表せば、
  \(
  \begin{eqnarray}
  \left\{
  \begin{aligned}
  \hat{A}|u_1\rangle&=|v\rangle \ \ \ (3)\\
  \hat{A}|u_2\rangle&=|v\rangle \ \ \ (4)
  \end{aligned}
  \right.
  \end{eqnarray}
  \)
  ここで、
  \(\hat{A}^{-1}|v\rangle\)を考えた時、それを\(|u_1\rangle\)か、\(|u_2\rangle\)かを決める術はありません。
  よって逆が存在しないことになります。
  また、 \((4)-(3)\)を行うと、
  \(
  (4)-(3)=\hat{A}(|u_1\rangle-|u_2\rangle)=\mathbf{0}
  \)
  となります。この意味は、\(\hat{A}\)は\(\mathbf{0}\)ではない、いくつかのベクトルを消去する、ということを表現しています。

[adsense2]

ユニタリー演算子

---

ユニタリー演算子は演算子\(\hat{A}\)の逆演算子\(\hat{A}^{-1}\)が
\(\hat{A}\)のエルミート共役\(\hat{A}^{\dagger}\)に等しいとき、その演算子はユニタリー演算子だ、と定義されます。すなわち、
\(
\hat{A}^{-1}=\hat{A}^{\dagger}
\)
を満たすとき、と定義されます。
また、別の表現では
\(
\hat{A}^{\dagger}\hat{A}=\hat{A}\hat{A}^{\dagger}=\mathbf{1}
\)
という場合もありますが同じことです。
ユニタリー演算子はよく、\(\hat{U}\)という表記がされます。

• ユニタリー演算子の性質

  1. ユニタリー演算子はノルムを保存する。
     ユニタリー演算子が状態\(|u\rangle\)に作用した場合を考えます。この時、ノルムは自身の内積を取ればいいので、
     \(\langle u|\hat{A}^{\dagger}\)と\(\hat{A}|u\rangle\)を作用させればノルムになります。故に、
     \(
     \langle u|\hat{A}^{\dagger}\hat{A}|u\rangle=\langle u|u\rangle
     \)
     であり、ノルムは変わりません。
  2. ユニタリー演算子の固有値は絶対値\(\mathbf{1}\)を必ず含む。
     あるユニタリー演算子を\(\hat{U}\)と書き、固有値問題を
     \(
     \hat{U}|v\rangle=\lambda |v\rangle\ \ \ (5)
     \)
     と書きます。
     
     両辺のエルミート共役をとって、
     \(
     \displaystyle \langle v|\hat{U}^{\dagger} =\lambda^* \langle v|
     \)
     ユニタリー演算子の性質を使うと、
     \(
     \displaystyle \langle v|\hat{U}^{-1} =\lambda^* \langle v|
     \)
     右から\(\hat{U}\)を作用させて、
     \(
     \begin{align}
     \displaystyle \langle v|\hat{U}^{-1}\hat{U} &=\lambda^* \langle v|\hat{U} \\
     \displaystyle \langle v|\hat{U} &=\frac{1}{\lambda^*}\langle v| \ \ \ \ (6)
     \end{align}
     \)

     (5)に左から\(\langle v|\)を作用させると、
     \(
     \langle v|\hat{U}|v\rangle=\langle v|\lambda |v\rangle=\lambda\langle v |v\rangle\ \ \ (7)
     \)
     であり、また、内積を以下のように変形し、(6)を使うと、
     \(
     \displaystyle \langle v|\hat{U}|v\rangle=\frac{1}{\lambda^*}\langle v|v\rangle\ \ \ (8)
     \)
     従って、式(7),(8)は同じものから出発したので等しいはずで、
     \(
     \begin{align}
     \lambda\langle v |v\rangle&=\frac{1}{\lambda^*}\langle v|v\rangle \\
     &\rightarrow |\lambda|^2=1
     &\rightarrow |\lambda|=1
     \end{align}
     \)
     となるため、ユニタリー演算子の固有値は必ず絶対値1を含みます。
     ※これは、\(e^{i\theta},\ \ \ \theta\)は実数、であればいいと言っています。1である必要性はありません。

  3. 異なる固有値を持つユニタリー演算子の固有状態は直交する
     異なる２つの固有値を\(\lambda_1, \lambda_2\)と書き、
     それぞれの固有値に属する固有ベクトルを\(|v_1\rangle, |v_2\rangle\)と書くことにします。
     \(|v_2\rangle\)と\(|v_1\rangle\)による内積をそれぞれ考えると、
     \(
     \langle v_2|\hat{U}|v_1\rangle=\langle v_2|\lambda |v_1\rangle=\lambda_1\langle v_2 |v_1\rangle\ \ \ (9)
     \)
     と変形できるし、
     \(
     \langle v_2|\hat{U}|v_1\rangle=\frac{1}{\lambda_2^*}\langle v_2|v_1\rangle=\lambda_2\langle v_2|v_1\rangle \ \ \ (10)
     \)
     とも変形できます。最後の変形は2.の性質、絶対値1を持つことを利用しています。
     2つの固有値\(\lambda_1, \lambda_2\)は違う値を仮定したので、(9)=(10)が成り立つためには
     \(\langle v_2|v_1\rangle=0\)
     でなければなりません。よって、ユニタリー演算子の異なる固有値に属する固有状態は直交していなければなりません。

ユニタリー演算子とエルミート演算子

---

エルミート演算子からユニタリー演算子を作る方法を示します。
この方法は運動量演算子の導出でも用いるので、覚えておいて損はないかと思います。

\(\hat{A}\)がエルミート演算子ならば、\(e^{i\hat{A}}\)はユニタリー演算子である。
演算子\(e^{i\hat{A}}\)の逆行列を考えて、それがエルミート共役に等しくなるか、見てみます。
定数に対するエルミート共役は単なる複素共役、\(\hat{U}=\hat{U}^{\dagger}\)であることを利用すると、
\(
\begin{align}
\left(e^{i\hat{A}}\right)^{-1}&=e^{-i\hat{A}} \\
&=1+(-i\hat{A})+\frac{(-i\hat{A})^2}{2!}+\cdots \\
&=1+(i\hat{A})^{\dagger}+\frac{\left\{(i\hat{A})^{\dagger}\right\}^2}{2!}+\cdots \\
&=\left(e^{i\hat{A}}\right)^{\dagger}
\end{align}
\)
となり、ユニタリー演算子の定義\(\hat{U}^{-1}=\hat{U}^{\dagger}\)を満たしていることがわかります。

逆行列とユニタリー行列

---

行列表記と演算子表記は同じものです。
量子力学では、ユニタリー行列の逆行列に関心があります。数式ならば、
\(\hat{U}^{-1}_{ij}=\hat{U}^{\dagger}_{ij}=\hat{U}^{*}_{ji}\)
ということです。

ユニタリー行列の性質の一つに、ユニタリー行列の列ベクトルは正規直交ベクトルである、ことを示しましょう。
逆行列との積は\(\mathbf{1}\)に等しいので
\(
(\hat{U}^{-1}\hat{U})_{ik}=\delta_{ik}
\)
です。これを踏まえ、ユニタリー演算子の性質を使って、
\(
\begin{align}
(\hat{U}^{\dagger}\hat{U})_{ik}&=\sum_j\hat{U}_{ij}^{\dagger}\hat{U}_{jk} \\
&=\sum_j\hat{U}_{ji}^{*}\hat{U}_{jk}=\delta_{ik}
\end{align}
\)
という結果が得られます。最後の式から、行列\(U\)の2つの列ベクトルの内積、これが\(\delta_{ik}\)に等しいことがわかります。
故にユニタリー行列の列ベクトルは正規直交ベクトルであることが示されました。

ちなみに、逆行列を得るための一般的な手続きは、
①  行列を対角形に変形
↓
②  対角要素を逆数に
↓
③  逆変換
という流れで行われます。