二重振り子

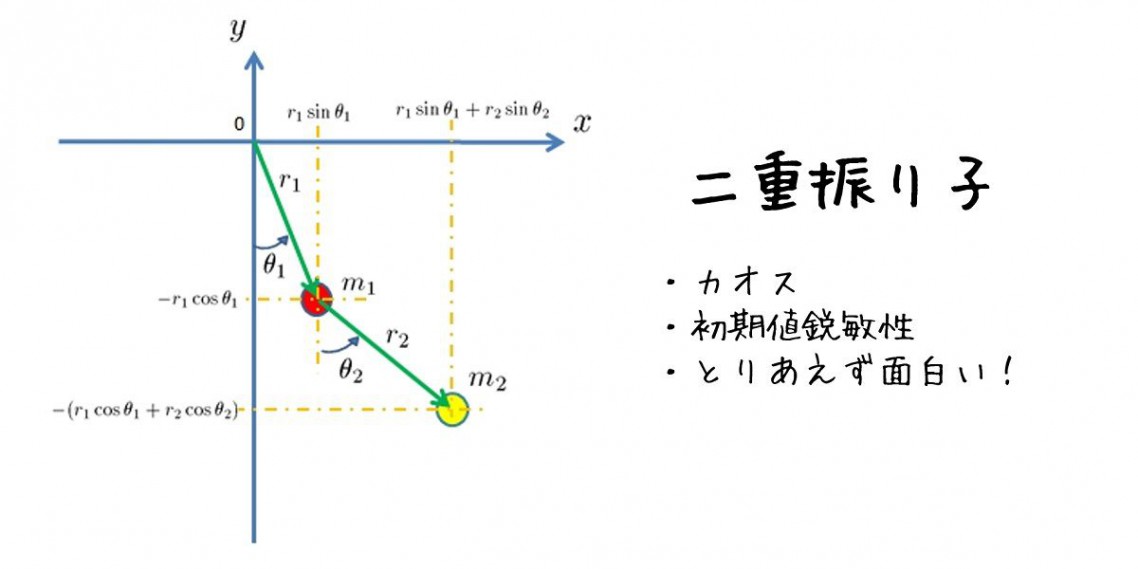
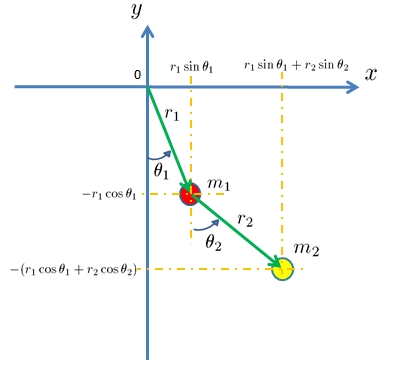
座標の取り方は下図のように取ります。棒の伸び縮みは無いものとします。

どういう解き方でもいいですが、ここでは

デカルト座標\(L(x,y)\)でラグランジアンを記述
デカルト座標から座標変換し、\((r,\theta)\)でラグランジアンを記述
新たな座標系で運動方程式を導く

という順で解いていきます。

[adsense1]

1, デカルト座標でのラグランジアンLは(運動エネルギーK)-(位置エネルギーU)と書けるため、
\(
L(x_1,\dot{x}_1,y_1,\dot{y}_1,x_2,\dot{x}_2,y_2,\dot{y}_2)\\
\displaystyle =\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2)+\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_2^2)-(-m_1gy_1-m_2gy_2)
\)
と書けます。

2, デカルト座標から座標変換
式を簡単にするために座標変換を行います。新しい座標\((r_1,\theta_1,r_2,\theta_2)\)とデカルト座標\((x_1,y_1,x_2,y_2)\)の関係式は
\(
\begin{align}
x_1&=r_1\sin{\theta_1}\\
y_1&=-r_1\cos{\theta_1}\\
x_2&=r_1\sin{\theta_1}+r_2\sin{\theta_2}\\
y_2&=-r_1\cos{\theta_1}-r_2\cos{\theta_2}
\end{align}
\)
という関係があります。各々を時間で微分すれば、
\(
\begin{align}
\dot{x}_1&=\dot{r}_1\sin{\theta_1}+r_1\dot{\theta}_1\cos{\theta_1}\\
\dot{y}_1&=-\dot{r}_1\cos{\theta_1}+r_1\dot{\theta}_1\sin{\theta_1}\\
\dot{x}_2&=\dot{r}_1\sin{\theta_1}+r_1\dot{\theta}_1\cos{\theta_1}+\dot{r}_2\sin{\theta_2}+r_2\dot{\theta}_2\cos{\theta_2}\\
\dot{y}_2&=-\dot{r}_1\cos{\theta_1}+r_1\dot{\theta}_1\sin{\theta_1}-\dot{r}_2\cos{\theta_2}+r_2\dot{\theta}_2\sin{\theta_2}
\end{align}
\)
これらをラグランジアン\(L(x_1,\dot{x}_1,y_1,\dot{y}_1,x_2,\dot{x}_2,y_2,\dot{y}_2)\)に代入します。すると、新たな座標系でのラグランジアン\(L(r_1,\dot{r}_1,\theta_1,\dot{\theta}_1,r_2,\dot{r}_2,\theta_2,\dot{\theta}_2)\)が得られます。
\(
\begin{align}
L(r_1,\dot{r}_1,\theta_1,\dot{\theta}_1,& r_2,\dot{r}_2,\theta_2,\dot{\theta}_2) \\
=&\frac{1}{2}m_1(\dot{r}_1^2+r_1^2\dot{\theta}_1^2)+\frac{1}{2}m_2\left[\dot{r}_1^2+\dot{r}_2^2+r_1^2\dot{\theta}_1^2+r_2^2\dot{\theta}_2^2 \right. \\
&\left.+2(\dot{r}_1 r_2 \dot{\theta}_2-r_1\dot{r}_2 \dot{\theta}_1)\sin{(\theta_1-\theta_2)}+2(\dot{r}_1 \dot{r}_2 +r_1 r_2 \dot{\theta}_1 \dot{\theta}_2)+\cos{(\theta_1-\theta_2)}\right] \\
&+m_1gr_1\cos{\theta_1}+m_2g(r_1\cos{\theta_1}+r_2\cos{\theta_2})
\end{align}
\)

僕は先ほど式を簡単にするために座標変換をする、といいました。しかし、新しい座標系におけるラグランジアンはどう見ても元のデカルト座標系のラグランジアンに比べて複雑です。この理由は物理的な意味から来ています。
振り子をつないでいる棒が伸び縮みしないとすると系の自由度は角度\(\theta_1,\theta_2\)の２つです。
となると運動方程式は最高で2本の独立した方程式になるはずです。
しかし、デカルト座標の場合うまく自由度を落とすことができず、運動方程式は4つになってしまいます。
そこで棒が伸び縮みを簡単に表すことができる座標系に移ることでうまく方程式の数を減らせます。

新しい座標系でのラグランジアンで棒の伸び縮みがないという条件を表すには
\(
\begin{align}
r_1&=l_1\ (l_1\mbox{は定数}) \\
r_2&=l_2\ (l_2\mbox{は定数})
\end{align}
\)
と書けるわけで、また、
\(
\begin{align}
\dot{r}_1&=0 \\
\dot{r}_2&=0
\end{align}
\)
となるわけです。

\(m_1=m_2=m,\ l_1=l_2=l\)という場合を特に考えると、ラグランジアンは
\(
\displaystyle L(\theta_1,\dot{\theta}_1,\theta_2,\dot{\theta}_2)=ml^2\left[\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2+\dot{\theta}_1\dot{\theta}_2\cos{(\theta_1-\theta_2)}\right]+mgl(2\cos{\theta_1}+\theta_2)
\)
と書けます。あとはラグランジュの運動方程式を当てはめて計算します。

3, 新たな座標系で運動方程式を導く
保存力場中でのラグランジュの運動方程式は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}_1}\right)-\frac{\partial L}{\partial\theta_1}&=0 \\
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}_2}\right)-\frac{\partial L}{\partial\theta_2}&=0
\end{aligned}
\right.
\end{eqnarray}
\)
なので、代入し、\(\ddot{\theta}_1,\ddot{\theta}_2\)に関する運動方程式にすれば
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\ddot{\theta}_1&=\frac{1}{2}\left\{-\ddot{\theta}_2\cos{(\theta_1-\theta_2)}-\dot{\theta}_2^2\sin{(\theta_1-\theta_2)}-2\frac{g}{l}\sin{\theta_1} \right\} \\
\ddot{\theta}_2&=-\ddot{\theta}_1\cos{(\theta_1-\theta_2)}+\dot{\theta}_1^2\sin{(\theta_1-\theta_2)}-\frac{g}{l}\sin{\theta_2}
\end{aligned}
\right.
\end{eqnarray}
\)
となります。これは非線形の２階連立微分方程式です。カオスです。解けません。
数値計算で解きます。用いるのは4次ルンゲ・クッタ法です。