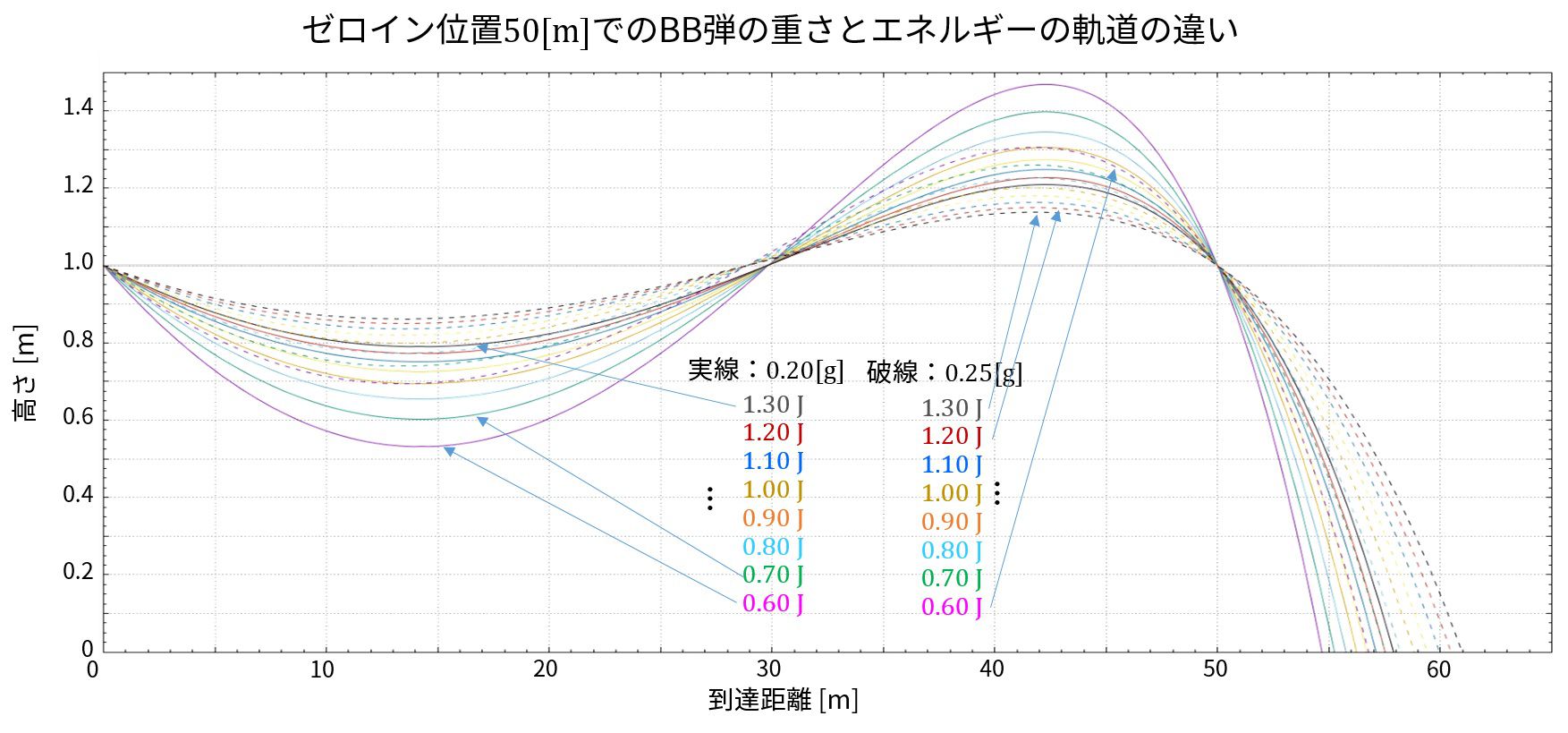
振り子の角度が小さいとき、また大きいときの振り子の取扱いです。
ラグランジアン\(L\)とハミルトニアン\(H\)から出発して運動方程式を求める方法を記述します。
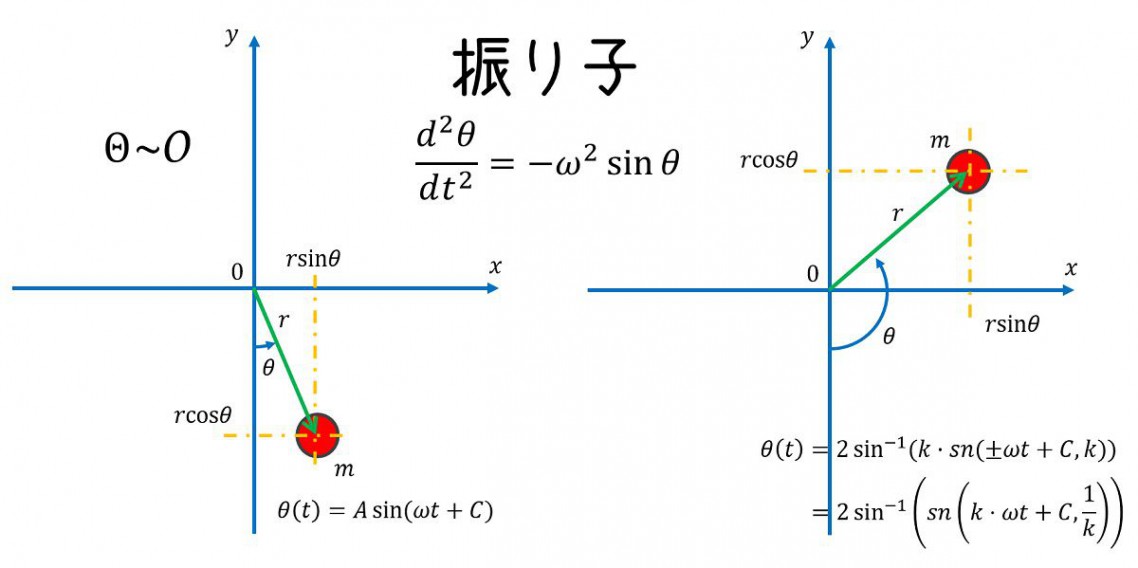
座標は図のようにとります。
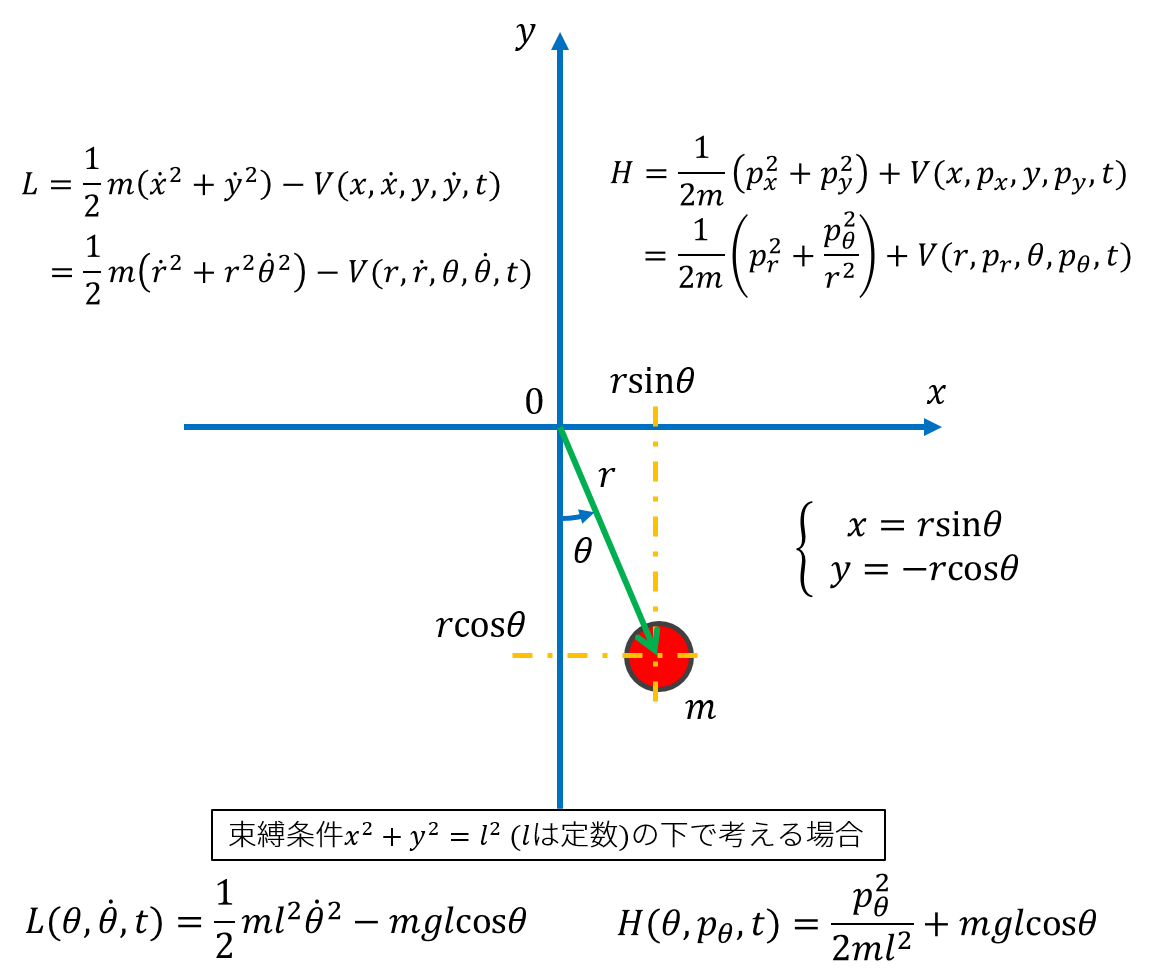
式で表せば、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
x&=r \sin{\theta} \\
y&=-r \cos{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
であり、1階微分は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\dot{x}&=\dot{r} \sin{\theta}+r\dot{\theta}\cos{\theta} \\
\dot{y}&=\dot{r} \cos{\theta} -r\dot{\theta}\sin{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
です。
[adsense1]
ラグランジアン\(L\)から出発
上の座標の元、デカルト座標\((x,y)\)での振り子のラグランジアン\(L(x,\dot{x},y,\dot{y},t)\)は
運動エネルギー\(K=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)\), ポテンシャルエネルギー\(V=V(x,\dot{x},y,\dot{y},t)\) より、
\(
\begin{align}
L(x,\dot{x},y,\dot{y},t)&=K-V \\
&=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)-V(x,\dot{x},y,\dot{y},t)
\end{align}
\)
と書けます。新たな座標系でのラグランジアン\(L(r,\dot{r},\theta,\dot{\theta},t)\)は\(\begin{eqnarray}
\left\{
\begin{aligned}
x&=r \sin{\theta} \\
y&=-r \cos{\theta}
\end{aligned}
\right.
\end{eqnarray}\)に従い座標変換をし、
\(
\displaystyle L(r,\dot{r},\theta,\dot{\theta},t)=\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r,\dot{r},\theta,\dot{\theta},t)
\)
とすることで新しい座標でのラグランジアンが得られます。
ここまでは一般的な話です。
今、もしも振り子をつないでいる棒が時間変化しない、言い換えれば束縛条件\(x^2+y^2=l^2\),(ここで\(l\)は定数)の元で考える場合、ポテンシャルエネルギーVは
\(
\begin{align}
V&=V(x,\dot{x},y,\dot{y},t)=-mgy \\
&=V(r,\dot{r},\theta,\dot{\theta},t)=mgr\cos\theta
\end{align}
\)
であり、\(\dot{l}=0\)なので
\(
\displaystyle L(\theta,\dot{\theta},t)=\frac{1}{2}ml^2\dot{\theta}^2-mgl\cos\theta
\)
となります。
運動方程式を求めるにはラグランジュの運動方程式
\(
\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta}=0
\)
に代入し、計算します。
\(
\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta}&=0 \\
\frac{d}{dt}(ml^2\dot{\theta})+mgl\sin{\theta}&=0 \\
ml^2\ddot{\theta}&=-mgl\sin\theta \\
\ddot{\theta}&=-\frac{g}{l}\sin\theta
\end{align}
\)
となり\(\theta\)に関する微分方程式が導けました。
ハミルトニアン\(H\)から出発
ハミルトニアン\(H\)はラグランジアン\(L\)と一般化座標\(q_i\)と一般化運動量\(p_i\)を用いて、
\(
\displaystyle H(\vec{p},\vec{q},t)\equiv\sum_i p_i\dot{q}_i-L(\vec{q},\vec{\dot{q}},t)
\)
と定義されます。また、一般化運動量\(p_i\)は一般化座標\(q_i\)を用いて
\(
\displaystyle p_i=\frac{\partial L(q_i,\dot{q}_i,t)}{\partial \dot{q_i}}
\)
という関係で定義されます。
デカルト座標での一般化運動量\(p_x\)と\(p_y\)は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
p_x&=\frac{\partial L(x,\dot{x},y,\dot{y},t)}{\partial \dot{x}}=m\dot{x} \\
p_y&=\frac{\partial L(x,\dot{x},y,\dot{y},t)}{\partial \dot{y}}=m\dot{y}
\end{aligned}
\right.
\end{eqnarray}
\)
となるため、デカルト座標でのハミルトニアンは
\(
\begin{align}
H(x,p_x,y,p_y,t)&=p_x\dot{x}+p_y\dot{y}-\left\{\frac{1}{2}m(\dot{x}^2+\dot{y}^2)-V(x,\dot{x},y,\dot{y},t)\right\} \\
&=\frac{p_x^2}{m}+\frac{p_y^2}{m}-\left\{\frac{1}{2}m(\frac{p_x^2}{m^2}+\frac{p_y^2}{m^2})-V(x,\dot{x},y,\dot{y},t)\right\} \\
&=\frac{1}{2m}(p_x^2+p_y^2)+V(x,\dot{x},y,\dot{y},t)
\end{align}
\)
と求められます。
新たな座標系でのは一般化運動量\(p_r, p_{\theta}\)は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
p_r&=\frac{\partial L(r,\dot{r},\theta,\dot{\theta},t)}{\partial \dot{r}}=m\dot{r} \\
p_{\theta}&=\frac{\partial L(r,\dot{r},\theta,\dot{\theta},t)}{\partial \dot{\theta}}=mr^2\dot{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
なので、新たな座標系でのハミルトニアン\(H(r,p_r,\theta,p_{\theta},t)\)は
\(
\begin{align}
H(r,p_r,\theta,p_{\theta},t)&=p_r\dot{r}+p_{\theta}\dot{\theta}-\left\{\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r,\dot{r},\theta,\dot{\theta},t) \right\} \\
&=\frac{p_r^2}{m}+\frac{p_{\theta}^2}{mr^2}-\left\{ \frac{p_r^2}{2m}+r^2\frac{p_{\theta}^2}{2mr^4} – V(r,\dot{r},\theta,\dot{\theta},t) \right\} \\
&=\frac{1}{2m}\left(p_r^2+\frac{p_{\theta}^2}{r^2}\right) + V(r,\dot{r},\theta,\dot{\theta},t)
\end{align}
\)
と求められます。
今、もしも振り子をつないでいる棒が時間変化しない、言い換えれば束縛条件\(x^2+y^2=l^2\), (ここで\(l\)は定数) の元で考える場合\(r=l\)を代入し、ポテンシャルエネルギー\(V\)は
\(
\begin{align}
V&=V(x,\dot{x},y,\dot{y},t)=-mgy \\
&=V(l,\dot{l},\theta,\dot{\theta},t)=mgl\cos\theta
\end{align}
\)
と求められます。今、\(p_l=m\dot{l}=0\)なのでハミルトニアンは
\(
\displaystyle H(\theta,p_{\theta},t)=\frac{p_{\theta}^2}{2ml^2}+mgl\cos{\theta}
\)
となります。
ハミルトンの正準運動方程式
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial H}{\partial q_i}&=-\dot{p}_i \\
\frac{\partial H}{\partial p_i}&=\dot{q}_i
\end{aligned}
\right.
\end{eqnarray}
\)
に代入すれば
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{d p_{\theta}}{dt}&=-mgl\sin\theta \\
\frac{d \theta}{dt}&=\frac{p_{\theta}}{ml^2}
\end{aligned}
\right.
\end{eqnarray}
\)
より、\(p_{\theta}\)を消去すれば、
運動方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
と導けます。
振り子の運動方程式
今、解くべき方程式は
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
になります。
振り子の角度が小さいとき
まず、よく近似される角度が小さい時だけを議論するとします。
\(\sin\theta\)はテイラー展開より、
\(
\displaystyle \sin{\theta}= \theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots =\sum_{n=1}^{\infty}(-1)^{n+1}\frac{\theta^{2n-1}}{(2n-1)!}
\)
であるため、\(\theta\ll 1\)である場合は初めの1項だけ考慮し、
\(
\sin{\theta}\sim \theta
\)
と近似します。すると、
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta
\)
となります。
通常は解\(\theta(t)\)を\(C_1\sin(\sqrt{\frac{g}{l}}t)+C_2\cos(\sqrt{\frac{g}{l}}t)\)とか置いてしまいますが、今回は数学的な手順に従って導出します。
まず、\(\displaystyle\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}\)という量を計算すると、
\(
\displaystyle \frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=2\frac{d\theta}{dt}\cdot \frac{d^2\theta}{dt^2}
\)
という関係があることが分かります。これを利用すると2階微分を1階微分に落とすことができます。
まず、運動方程式の両辺に\(\displaystyle 2\frac{d\theta}{dt}\)を掛け、整理していきます。すなわち、
\(
\begin{align}
2\frac{d \theta}{dt}\cdot\frac{d^2 \theta}{dt^2}=-\frac{g}{l}2\frac{d \theta}{dt}\cdot\theta \\
\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=\frac{d}{dt}\left\{-\frac{g}{l}\theta^2\right\} \\
\left(\frac{d\theta}{dt}\right)^2=-\frac{g}{l}\theta^2+C_0
\end{align}
\)
となります。ここで\(\left(\frac{d\theta}{dt}\right)^2\)は\(\theta\)が虚数をとらない限り必ず正であることから、
\(-\pi\lt \theta\lt \pi\)の範囲で(ただし、\(\sin\theta\sim \theta\)の成り立つ近似の領域が\(\theta\)が小さい場合だけなので、まぁまぁ可能な範囲、として考えます。)
どんなに変化しても積分定数\(C_0\)はそれより大きい値(\(\left(\frac{d\theta}{dt}\right)^2\geq 0\)にする値、\(C_0\)は必ず正である。)でなければなりません。
それを考えながら左辺の2乗を取り払い、
\(
\begin{align}
\frac{d\theta}{dt} = \pm \sqrt{C_0-\frac{g}{l}\theta^2} \\
\pm \int \frac{1}{\sqrt{C_0-\frac{g}{l}\theta^2}}d\theta=\int dt
\end{align}
\)
となります。左辺を計算するため変数変換
\(
\displaystyle \sqrt{\frac{g}{l}}\theta=\sqrt{C_0}\sin\phi
\)
を行います。
\(
\displaystyle \frac{d \theta}{d\phi}=\sqrt{\frac{l}{g}C_0}\cos\phi
\)
なので
\(
\begin{align}
\displaystyle \int \frac{1}{\sqrt{C_0-\frac{g}{l}\theta^2}}d\theta
&=\displaystyle \int \frac{1}{\sqrt{C_0}\sqrt{1-\sin^2{\phi}}}\cdot\sqrt{\frac{l}{g}C_0}\cos{\phi}d\phi \\
&=\sqrt{\frac{l}{g}}\phi \\
&=\sqrt{\frac{l}{g}}\sin^{-1}\left(\sqrt{\frac{g}{lC_0}}\theta\right)
\end{align}
\)
と計算できるので、
\(
\begin{align}
\sqrt{\frac{l}{g}}\sin^{-1}\left(\sqrt{\frac{g}{lC_0}}\theta\right)=t+C_1 \\
\theta(t)=\sqrt{\frac{l}{g}C_0}\sin\left(\pm \sqrt{\frac{g}{l}}(t+C_1)\right)
\end{align}
\)
と書けます。\(C_0,C_1\)は単なる積分定数であるためにそれ自体の意味はなく、また、\(\sin\)の中の±は\(C_1\)を調節すれば関係なくなるので、それらを省略すれば
\(
\displaystyle \theta(t)=C_0\sin\left(\sqrt{\frac{g}{l}}t+C_1\right)
\)
となります。角周波数は
\(\displaystyle \omega=\sqrt{\frac{g}{l}}\)
となります。
角度が小さいときはこれでお仕舞いにします。
振り子の角度が大きいとき
楕円関数というものが計算を行っていくと出てきます。そこに至るまでの手順は振り子の角度が小さいときの手順に途中まで同じです。
対象になる問題は
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
です。ここで\(\sqrt{\frac{g}{l}}=\omega\)とおいて、
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\omega^2\sin\theta
\)
と書き直します。
振り子の角度が小さいときと同じようにまず2階微分を1階微分に焼直すため、両辺に\(\displaystyle 2\frac{d\theta}{dt}\)を掛けて、
\(
\begin{align}
2\frac{d \theta}{dt}\cdot\frac{d^2 \theta}{dt^2}=-\omega^2\frac{d \theta}{dt}\cdot \sin\theta \\
\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=\frac{d}{dt}\left\{2\omega^2\cos\theta\right\} \\
\left(\frac{d\theta}{dt}\right)^2=2\omega^2\cos(\theta)+C_0
\end{align}
\)
ここで左辺はゼロ以下になることはないため、そうなるように積分定数\(C_0\)を決めます。
ここでの積分定数\(C_0\)の持つ物理的な意味をちょっと考えます。
振り子には大きく分けて2種類の運動が存在します。1つは\(\theta\)が小さいときの運動の延長線上にある、最下点を中心として振動する運動であり、もう1つはぐるんぐるん回る運動です。
ちょっと違う言い方をすれば、1つ目の運動は必ず粒子の速度の大きさ\(|v|=l|\frac{d \theta}{dt}|\)=0になる時間が存在する運動を表し、2つ目の運動は常に速度の大きさ\(|v|\)がゼロではない有限の値を持つ運動を表します。
この運動の区別がこの積分定数\(C_0\)に依存するのです。
何はともあれ、数学的な話をしていけば2つの運動を記述する微分方程式はどちらも\(\displaystyle \frac{d^2\theta}{dt^2}=-\omega^2\sin\theta\)であるので、これが解ければ自然と両方の運動を記述する答えが得られるはずです。その区別は後で考えましょう。
つまり、言いたかったことは\(C_0\)はいつも\(2\omega^2\cos(\theta)\)以上ですよ、ということを言いたかったんです。
よって、左辺のルートを取り払います。
\(
\begin{align}
\left(\frac{d\theta}{dt}\right)^2 &=2\omega^2\cos(\theta)+C_0 \\
\frac{d\theta}{dt} &=\pm\sqrt{C_0+2\omega^2\cos(\theta)}
\end{align}
\)
天下り的ですが、ここで
\(
\displaystyle \cos\theta=1-2\sin^2{\frac{\theta}{2}}
\)
の関係式を使って、
\(
\begin{align}
\frac{d\theta}{dt} &=\pm\sqrt{C_0+2\omega^2\left(1-2\sin^2{\frac{\theta}{2}}\right)} \\
&=\pm \sqrt{(C_0+2\omega^2)}\sqrt{1-\frac{4\omega^2}{C_0+2\omega^2}\sin^2\frac{\theta}{2}} \\
&=\pm 2\omega k\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}
\end{align}
\)
となります。ここで\(\displaystyle \frac{1}{k}=\sqrt{\frac{4\omega^2}{C_0+2\omega^2}}\)という量\(k\)を定義しました。
なぜ\(\frac{1}{k}\)なの?という理由は後々都合がよくなるからです。深い意味はありません。
運動方程式は
\(
\begin{align}
\frac{d\theta}{dt}=\pm 2\omega k\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}
\end{align}
\)
とここまで簡略化されました。積分します。
\(
\displaystyle \pm\frac{1}{2\omega k}\int_{\theta_0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta=\int_{t_0}^{t} dt
\)
となります。積分区間は初期時刻\(t_0\)に角度\(\theta_0\)にいた質点が時刻\(t\)には角度\(\theta\)にいることを意味します。
通常、積分区間は積分定数\(C_1\)を使って表します。この積分区間は以下の変形が可能です。丁寧にやると、
\(
\begin{align}
\int_{\theta_0}^{\theta} f(\theta)d\theta &= \int_{t_0}^{t} g(t) dt \\
\int_{\theta_0}^{0} f(\theta)d\theta+\int_{0}^{\theta} f(\theta)d\theta &= \int_{t_0}^{0} g(t) dt+\int_{0}^{t} g(t) dt \\
\int_{0}^{\theta} f(\theta)d\theta &= \int_{0}^{t} g(t) dt + C_1
\end{align}
\)
です。よって
\(
\displaystyle \pm\frac{1}{2\omega k}\int_{0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta=\int_{0}^{t} dt + C_1
\)
を解けば良いことになります。左辺の積分を解きましょう。
変数変換\(\frac{1}{k}\sin\frac{\theta}{2}=\sin{\phi}\)を行います。
\(
\begin{align}
\frac{d}{d\phi}\left(\frac{1}{k}\sin\frac{\theta}{2}\right)&=\frac{d}{d\phi}\sin\phi \\
\frac{1}{k}\cos\left(\frac{\theta}{2}\right)\frac{1}{2}\frac{d \theta}{d\phi} &= \cos\phi \\
\frac{d \theta}{d\phi} &= 2k \frac{\cos{\phi}}{\cos\frac{\theta}{2}}
\end{align}
\)
となります。積分区間は
\(
\begin{align}
&\theta\ \ | 0 \rightarrow \ \theta \\
&\phi\ \ | 0 \rightarrow \ \phi(=\sin^{-1}(\frac{1}{k}\sin{\frac{\theta}{2}})) \\
\end{align}
\)
と変化します。左辺に代入すれば、
\(
\begin{align}
\pm\frac{1}{2\omega k}\int_{0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta
&=\pm\frac{1}{2\omega k}\int_{0}^{\phi} \frac{1}{\sqrt{1-\sin^2\phi}}2k\frac{\cos{\phi}}{\cos\frac{\theta}{2}} d\phi \\
&=\pm \frac{1}{\omega} \int_{0}^{\phi} \frac{1}{\cos\frac{\theta}{2}}d\phi \\
&=\pm \frac{1}{\omega} \int_{0}^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi \\
\end{align}
\)
となります。故に、
\(
\displaystyle \int_{0}^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi =\pm\omega t+C_1
\) …(A)
と表されます。左辺の積分は楕円積分と呼ばれています。
第一種Legendre楕円積分は
\(
\displaystyle F(\phi, k)=\int_0^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi
\)
と定義されます。この逆関数の\(sin\)はJacobiの楕円関数\(sn(u,k)\)をして定義されています。
どういうことかといえば、\(u=F(\phi, k)\)のとき、\(\phi=F^{-1}(u,k)\)であるので、
\(
\sin\phi=\sin(F^{-1}(u,k))=sn(u,k)
\)
という関数を定義するのです。
すると、今、\(\pm \omega t+C_1=F(\phi, k)\)であるため、
\(
\begin{align}
\pm \omega t+C_1&=F(\phi, k)=u \\
\phi&=F^{-1}(\pm \omega t+C_1, k) \\
\sin\phi &=\sin(F^{-1}(u,k)) \\
\sin\phi &=sn(u,k)
\end{align}
\)
となります。
\(\sin\phi=\frac{1}{k}\sin\frac{\theta}{2}\)なので求めたかった\(\theta(t)\)は
\(
\begin{align}
\sin{\frac{\theta}{2}}=k\ sn(\pm\omega t+C_1, k) \\
\theta(t)=2\sin^{-1}(k\ sn(\pm\omega t+C_1, k))
\end{align}
\)
と求められます。
[adsense2]
Jacobiの楕円関数は数値計算的にはランデンの方法という方法で計算されるそうです。
さて、式(A)を見ていると、kが1以上の場合、なんかおかしいことに気が付くかと思います。もしもkが1以上の場合、被積分関数のルートの中が負になることがあり得るんじゃ・・・?
実はこの状況が生まれることはありません。これは積分範囲が今\(0\sim\phi\)になっていますが、\(\phi=\sin^{-1}(\frac{1}{k}\sin{\frac{\theta}{2}})\)であらわされる区間なので、kの値に応じてとりうる積分範囲は必ずルートの中が負にならない範囲に収まるのです。
ただ、上の問題を心配する必要が無いようにkの範囲は\(0\le k\le 1\)に通常は制限されます。
k=2の楕円関数は存在するのに範囲が制限されて、計算どうするの?という疑問が生まれます。
これを解決するのはJacobiの楕円関数snの性質を利用します。
Jacobiの楕円関数は三角関数の拡張であるとみなせるので、その性質は非常に多岐にわたります。
その中の一つにこういう関係式があります。
\(
\displaystyle sn(u,\frac{1}{k})=k\ sn(\frac{u}{k},k)
\)
これを使うとkが1より大きい時でも変換することができます。
具体的には、
\(
\begin{eqnarray}
\theta(t)=
\left\{
\begin{aligned}
& 2\sin^{-1}(k\ sn(\pm\omega t+C_1, k)) \dots (0 \lt k \lt 1) \\
& 2\sin^{-1}(sn(k \omega t+C_1),\frac{1}{k}) \dots (1\lt k)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。運動の状態と対応させるのであれば、一つ目の式\((k\lt 1)\)の場合は往復運動をし、\((k\gt 1)\)の時はぐるんぐるん回る運動に対応します。
1往復、または1回転に要する時間Tは
\(
\begin{eqnarray}
T=
\left\{
\begin{aligned}
&\frac{4}{\omega}K(k) \dots (0 \lt k \lt 1) \\
&\frac{2}{k\omega}K(\frac{1}{k}) \dots (1 \lt k1)
\end{aligned}
\right.
\end{eqnarray}
\)
として与えられます。ここでK(k)は第1種完全楕円積分で、
\(
\displaystyle K(k)=\int_0^1 \frac{1}{\sqrt{(1-x^2)(1-k^2 x^2)}}dx
\)
という定積分です。
※
例えば、微分方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\sin\theta
\)
を
\(
t=0,\; \theta=0; \frac{d\theta}{dt}=1.9 (k=0.95)
\)
の初期条件の下解いた場合、
1周期\(T\)は
\(
T=4K(0.95)=10.360044923498004876778\cdots
\)
となります。
この値はwolfram alphaから求めました。
4*EllipticK[0.95*0.95] wolfram alpha
wolfram alphaでの第1種完全楕円積分は
\(
\displaystyle EllipticK[k’]=\int_0^1 \frac{1}{\sqrt{(1-x^2)(1-k’ x^2)}}dx
\)
として定義されているので注意が必要です。
参考文献
森口繁一, 宇田川銈久, 一松信著『数学公式Ⅲ 特殊関数』岩波書店(1960)p.40~45
Hamilton の正準運動方程式 -epii’s physics notes
KIT -数学ナビゲーション
振り子と楕円関数
Jacobi Elliptic Functions — from Wolfram MathWorld