忘れやすいラグランジュの未定乗数法のメモです。
一通り学んだ人が使い方を思い出す、という状況を想定しています。
変数が独立な場合
3変数x,y,zが独立(xが変化してもy,zは変化しない、\(\vec{x}\cdot\vec{y}=0\) (y,zも同様))で、その関数\(f(x,y,z)\)の極値は
\(
\displaystyle \frac{\partial f}{\partial x}=0,\ \ \frac{\partial f}{\partial y}=0,\ \ \frac{\partial f}{\partial z}=0 \ \ \cdots (1)
\)
を連立させて解くことで得られます。
変数が独立ではない(従属な)場合
変数x,y,zの間に関係式
\(
g(x,y,z)=c, \ \mbox{$c$は定数} \ \ \cdots (2)
\)
という条件がある場合、
- 式(2)が(例えば)zについて解けるならば、\(f(x,y,z(x,y))\)として2変数\(x,y\)の極値問題として解ける。
- \(z=z(x,y)\)の形に書けない場合 →ラグランジュの未定乗数法を使う
- の場合、”関数\(f(x,y,z)\)が極値をとる”、とは
\(
\displaystyle df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz=0 \ \ \cdots (3)
\)
である点(極値点)である。
→極値点から\(x,y,z\)を任意の微小量\(dx,dy,dz\)だけ変化させても関数\(f(x,y,z)\)の変化分である\(df\)は1次の範囲でゼロです。
故に任意の\(dx,dy,dz\)について(3)が成立する、よって(1)が導かれることになります。
- の場合、\(dx,dy,dz\)は独立に選ぶことができません。その取り方は条件(2)に従います。
極値点まわりで(2)が成立しているならば、
\(
g(x+dx,y+dy,z+dz)=g(x,y,z)\ \ \cdots (4)
\)
を満たすような\(dx,dy,dz\)の変化しか許されないことになります。この条件から\(dx,dy,dz\)の動かし方は、
\(
\displaystyle \frac{\partial g}{\partial x}dx+\frac{\partial g}{\partial y}dy+\frac{\partial g}{\partial z}dz=0 \ \ \cdots (5)
\)
に制限されます。
条件(5)を\(dz\)について変形すると、
\(
\displaystyle dz=-\frac{\frac{\partial g}{\partial x}dx+\frac{\partial g}{\partial y}dy}{\frac{\partial g}{\partial z}} \ \ \cdots (6)
\)
となります。式(3)へ式(6)を代入すると
\(
\begin{align}
\displaystyle df &=\left( \frac{\partial f}{\partial x}-\frac{\frac{\partial g}{\partial x}}{\frac{\partial g}{\partial z}}\frac{\partial f}{\partial z}\right)dx
+\left( \frac{\partial f}{\partial y}-\frac{\frac{\partial g}{\partial y}}{\frac{\partial g}{\partial z}}\frac{\partial f}{\partial z}\right)dy=0 \\
&=\left( \frac{\partial f}{\partial x}-\lambda\frac{\partial g}{\partial x}\right)dx
+\left( \frac{\partial f}{\partial y}-\lambda\frac{\partial g}{\partial y}\right)dy=0 \ \ \cdots (7)
\end{align}
\)
ここで
\(
\displaystyle \lambda=\frac{\frac{\partial f}{\partial z}}{\frac{\partial g}{\partial z}}\ \ \cdots (8)
\)
と置きました。この\(\lambda\)はラグランジュの未定乗数と呼ばれます。
未定乗数という所以は、この\(\lambda\)をあらわに決める必要はなく、決まらない定数のままでも極値点を求めることができるという事を表しています。
今、\(dx,dy\)は独立であるので(※1)、その係数は\(0\)になるはずです。故に、式(7)と式(8)より、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial f}{\partial x}-\lambda\frac{\partial g}{\partial x}&=0 \\
\frac{\partial f}{\partial y}-\lambda\frac{\partial g}{\partial y}&=0 \\
\frac{\partial f}{\partial z}-\lambda\frac{\partial g}{\partial z}&=0
\end{aligned}
\right.
\end{eqnarray}
\)
が導けます。変形をすれば、条件式(2)も含めて、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial}{\partial x}\left(f-\lambda g\right)&=0 \\
\frac{\partial}{\partial y}\left(f-\lambda g\right)&=0 \\
\frac{\partial}{\partial z}\left(f-\lambda g\right)&=0 \\
g(x,y,z)&=c
\end{aligned}
\right.
\end{eqnarray}
\ \ \ \cdots (9)
\)
と書くことができます。未知の変数は\(x,y,z,\lambda\)の4つで、方程式は4本なので解くことができます。
この式が言うことは、束縛条件\(g(x,y,z)=c\)があった場合、関数\(f-\lambda g\)を考えて、その極値を求めればよいことを表しています。
[adsense1]
まとめ
条件\(g(x,y,z)=c\)がある関数f(x,y,z)の極値問題は、
\(
\tilde{f}=f-\lambda g \ \ \cdots (10)
\)
という新たな関数\(\tilde{f}\)を考えるとx,y,zが独立に変化するものと考えて\(\tilde{f}(x,y,z)\)の極値問題を考えればよい、となります。
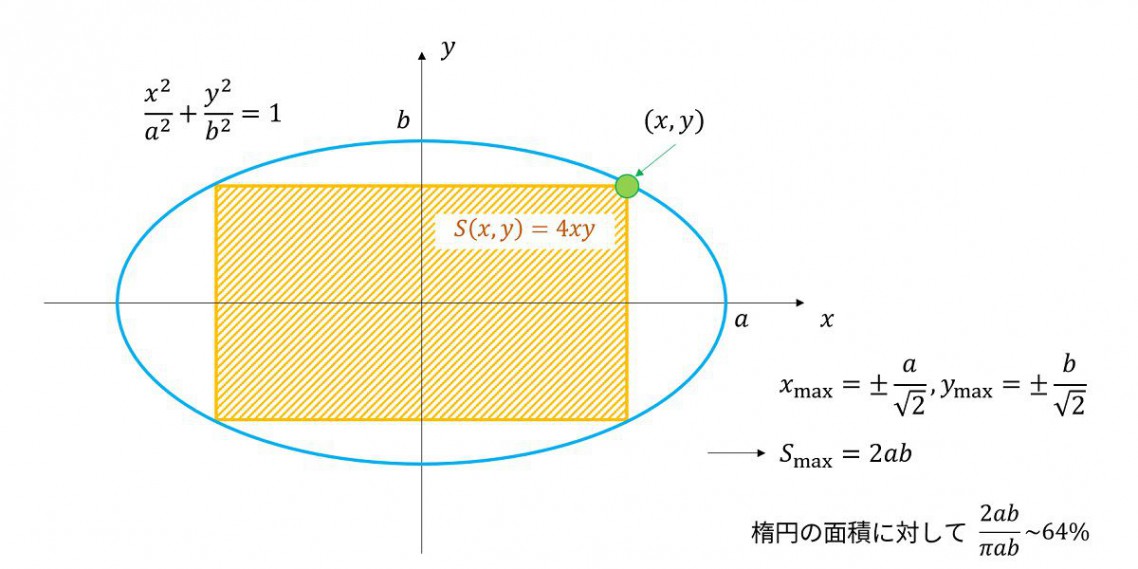
例題 ~楕円に内接する長方形の面積の最大値を求める~
楕円の方程式は
\(
\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
であり、この方程式の許す\(x,y\)を満たしながら、内接する長方形の面積
\(S(x,y)=4xy\)
を最大にする\(x,y\)を求めます。
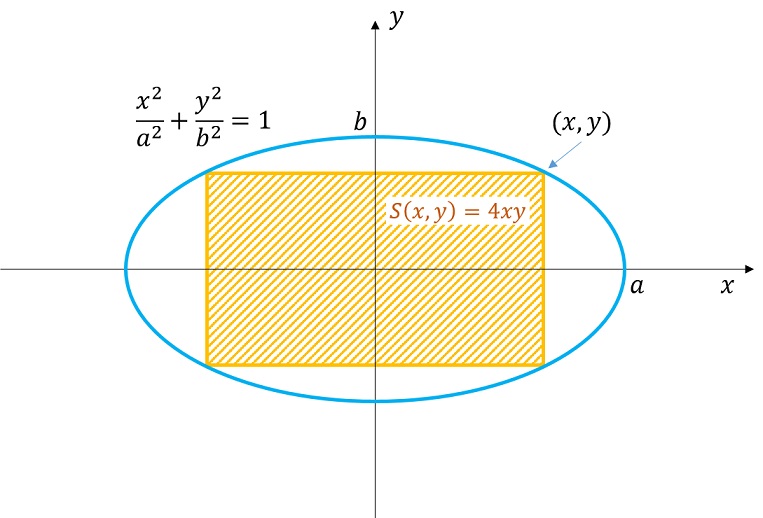
これは、関数\(f(x,y)=4xy\)の極値を\(\displaystyle g(x,y)=\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)という条件下で解く、という意味になります。
まず、\(\tilde{S}\)を式(10)より求めます。
\(
\begin{align}
\tilde{S}&=S-\lambda g \\
&=4xy-\lambda\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}\right)
\end{align}
\)
式(9)より、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial \tilde{S}}{\partial x}&=0 \\
\frac{\partial \tilde{S}}{\partial y}&=0
\end{aligned}
\right.
\end{eqnarray}
\)
を考えればいいので、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial \tilde{S}}{\partial x}=4y-\lambda \frac{2x}{a^2}&=0 \ \ \cdots (i)\\
\frac{\partial \tilde{S}}{\partial y}=4x-\lambda \frac{2y}{b^2}&=0 \ \ \cdots (ii)\\
\frac{x^2}{a^2}+\frac{y^2}{b^2}&=1 \ \ \cdots (iii)
\end{aligned}
\right.
\end{eqnarray}
\)
を満たす未知の変数\(x,y,\lambda\)が\(S\)の極値となっています。
(i)と(ii)より\(\lambda\)を消去すると
\(
\begin{align}
(i) &\rightarrow \lambda=\frac{2y}{x}a^2 \\
(ii) &\rightarrow 4x-\left(\frac{2y}{x}a^2\right)\frac{2y}{b^2}=0
\end{align}
\)
なので
\(
\displaystyle \frac{x^2}{a^2}=\frac{y^2}{b^2}
\)
(iii)に代入して
\(
\displaystyle 2\frac{x^2}{a^2}=1
\)
より
\(\displaystyle x=\pm\frac{a}{\sqrt{2}},\ \ y=\pm\frac{b}{\sqrt{2}}\)
のとき\(S(x,y)\)が極値を取ることがわかります。
ちなみに、この時の長方形の面積\(S_{max}\)は\(S_{max}=2ab\)であり、
これは楕円の面積\(S=\pi ab\)の\(\frac{2ab}{\pi ab}\sim 0.64\)となり、約64%を占めていることになります。
[adsense2]
※1
x,yが独立であるのは、x,y,zをつなぐ1本の条件式\(g(x,y,z)=c\)によって消え得る変数は1つだけであるためです。
参考
小野寺 嘉孝著 『物理のための応用数学』裳華房(1988)p.6~10