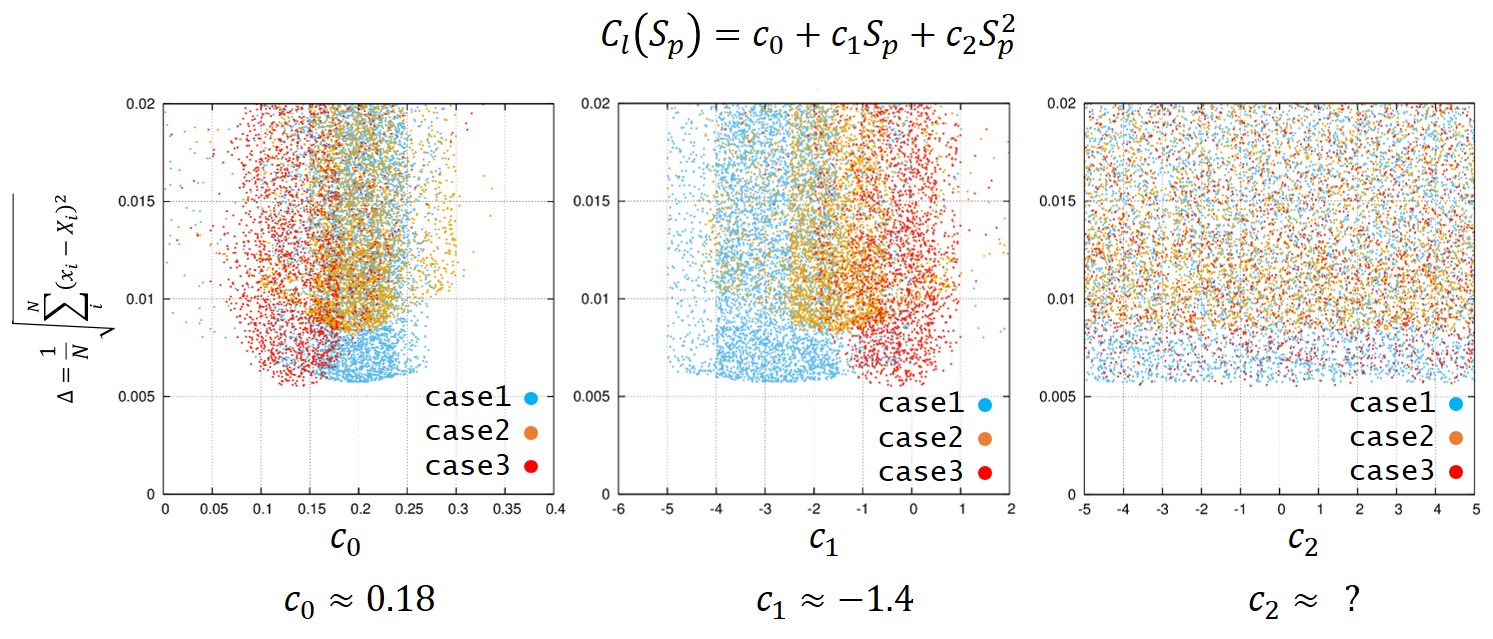
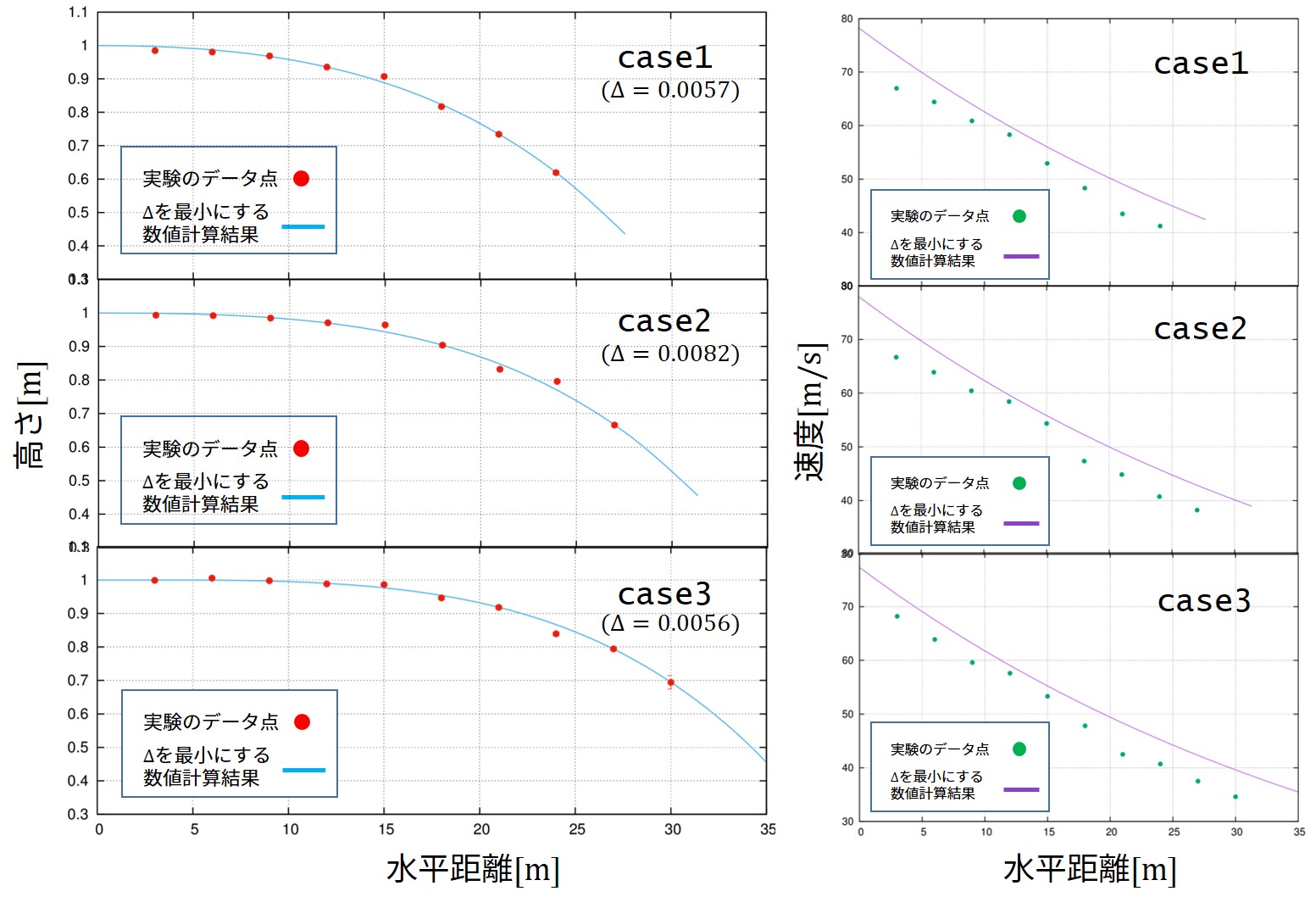
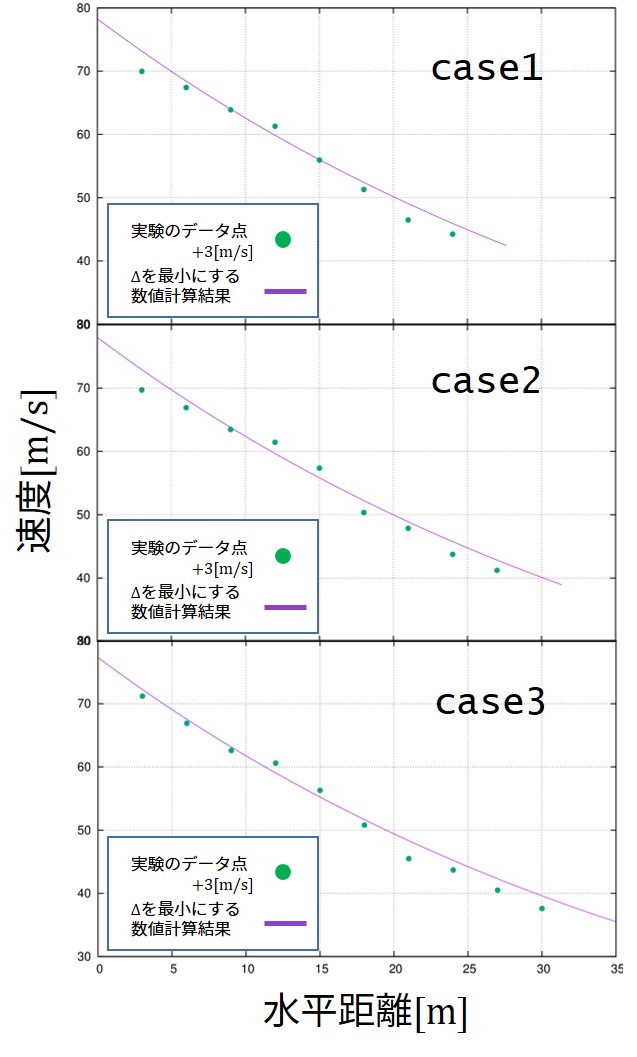
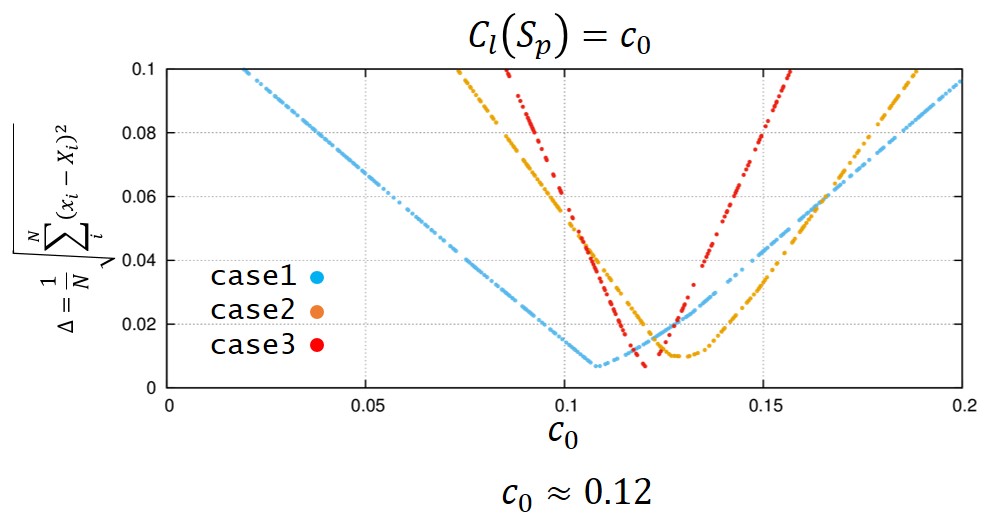
module GBL
!sikinote http://slpr.sakura.ne.jp/qp/
!Author : sikino
!Date : 2016/03/18 (yyyy/mm/dd)
! : 2016/03/20
! : 2016/07/23
! : 2016/07/25
! : 2016/08/06
implicit none
!Constant of system
double precision::m,g,a,eta,rho,temperature,pressure,moisture
character(48)::omgdecay
!Example parameter
! 1, tol=1d-10, eps=1d-9
! => very exact, slow computing speed
! 2, tol=1d-6, eps=1d-6
! => enough computation practically.
!Accuracy of rungekutta(tol must be constant)
! 1d-2 < tol : Rouph condition, computing speed is fast.
! 1d-10 < tol < 1d-2 : Intermediate
! 1d-12 < tol < 1d-10 : Exact condition, computing speed is slow.
! tol < 1d-12 : Not reccomended, Maybe cannot computing due to machine epsilon.
double precision,parameter::tol=1d-10
!Conversence epsilon at rootfinding method
! 1d0 < eps : Rouph condition, computing speed is fast.
! 1d-10 < eps < 1d0 : Intermediate
! eps < 1d-10 : Exact condition, computing speed is slow.
! or cannot converge less than 1d-10.
double precision,parameter::eps=1d-7
end module GBL
!================================
function rho_humid(T,P,M)
! T : temperature [degree]
! P : pressure [Pa] ( 1 atm = 101325 Pa )
! M : moisture [no-dimension]
implicit none
double precision,intent(in)::T,P,M
double precision::rho_humid,et,rhoair
et=6.1078d0*10d0**(7.5d0*T/(T+237.3d0)) ! et[hPa]
et=100d0*et
et=M*et
!write(6,*)"et[Pa]",et
rhoair=0.0034856447d0*P/(T+273.15d0-0.670d0)
rho_humid=rhoair*(1d0-0.378d0*et/P)
return
end function rho_humid
function eta_air(T)
! T : temperature [degree]
implicit none
double precision::T,eta_air
eta_air=1.487d-6*((T+273.15d0)**1.5d0)/((T+273.15d0)+117d0)
return
end function eta_air
module RKmod
!sikinote http://slpr.sakura.ne.jp/qp/
!developer => sikino
!date => 2015/07/13
implicit none
!For Butcher table
integer,private::s
double precision,private,allocatable::a(:,:),b1(:),b2(:),c(:),Rc(:)
!-----------------------------
contains
subroutine rk_preparation(method)
!set Butcher table
implicit none
character(*)::method
if(trim(method).eq."rk4")then
s=4
allocate(a(1:s,1:s),b1(1:s),c(1:s))
a=0d0; b1=0d0; c=0d0
c(1:4)=(/0d0, 0.5d0, 0.5d0, 1d0/)
a(1,1:4)=(/0d0,0d0,0d0,0d0/)
a(2,1:4)=(/0.5d0,0d0,0d0,0d0/)
a(3,1:4)=(/0d0,0.5d0,0d0,0d0/)
a(4,1:4)=(/0d0,0d0,1d0,0d0/)
b1(1:4)=(/1d0/6d0, 1d0/3d0, 1d0/3d0, 1d0/6d0/)
elseif(trim(method).eq."rkf45")then
s=6
allocate(a(1:s,1:s),b1(1:s),b2(1:s),c(1:s),Rc(1:s))
a=0d0; b1=0d0; b2=0d0; c=0d0; Rc=0d0
c(1:6)=(/0d0, 0.25d0, 3d0/8d0, 12d0/13d0, 1d0, 0.5d0/)
a(1:6,1:6)=0d0
a(1,1:6)=(/0d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(2,1:6)=(/0.25d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(3,1:6)=(/0.09375d0, 0.28125d0, 0d0, 0d0, 0d0, 0d0/)
a(4,1:6)=(/1932d0/2197d0, -7200d0/2197d0, 7296d0/2197d0, 0d0, 0d0, 0d0/)
a(5,1:6)=(/439d0/216d0, -8d0, 3680d0/513d0, -845d0/4104d0, 0d0, 0d0/)
a(6,1:6)=(/-8d0/27d0, 2d0, -3544d0/2565d0, 1859d0/4104d0, -11d0/40d0, 0d0/)
b2(1:6)=(/16d0/135d0, 0d0, 6656d0/12825d0, 28561d0/56430d0, -9d0/50d0, 2d0/55d0/)
b1(1:6)=(/25d0/216d0, 0d0, 1408d0/2565d0, 2197d0/4104d0, -0.2d0, 0d0/)
Rc(1:6)=(/1d0/360d0,0d0,-128d0/4275d0,-2197d0/75240d0,1d0/50d0,2d0/55d0/)
else
write(6,*)"program stop at rk_preparation"
stop
end if
return
end subroutine rk_preparation
!------------------------------
subroutine rk_deallocation(method)
implicit none
character(*)::method
if(trim(method).eq."rk4")then
deallocate(a,b1,c)
elseif(trim(method).eq."rkf45")then
deallocate(a,b1,b2,c,Rc)
else
write(6,*)"program stop at rk_deallocation"
stop
end if
return
end subroutine rk_deallocation
!-------------------
subroutine rkf451(func,N,x,h,y,xbound,info,tol,ik)
!------------
!info = -2 (Failed. calclation range has already over.)
! = -1 (Failed.
! h becomes too small. change tol or check condition of func.)
! = 0 (Success. running now)
! = 1 (Success. x reach xbound normally)
!------------
implicit none
interface
function func(iN,ix,iy,is,iik)
implicit none
integer,intent(in)::iN,is,iik
double precision,intent(in)::ix,iy(1:iN)
double precision::func
end function func
end interface
integer,intent(in)::N,ik
double precision,intent(in)::xbound
double precision,intent(in)::tol
double precision,intent(inout)::x,h,y(1:N)
integer,intent(inout)::info
double precision,parameter::hmin=1d-14,hmax=1.d0
integer::i,j,FLAG
double precision::R,delta,tx,tmp(1:N),K(1:s,1:N),Sy,err
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
FLAG=1
if(abs(x-xbound).le.1d-15)then
info=1
FLAG=0
else
if(abs(h).le.1d-15)then
write(6,*)"maybe overflow or underflow, please change tol."
write(6,'(A)')"====Err info===="
write(6,'(A,e17.9e3)')"x --> ",x
write(6,'(A,e17.9e3)')"h --> ",h
do i=1,N
write(6,'(A,i0,A,e17.9e3)')"y(",i,") --> ",y(i)
enddo
write(6,'(A)')"================"
info=-1
FLAG=0
stop
endif
if(h.le.0d0.and.xbound-x.ge.0d0)then
info=-2
FLAG=0
elseif(h.gt.0d0.and.xbound-x.le.0d0)then
info=-2
FLAG=0
endif
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
tmp(1:N)=y(1:N)
do i=1,j-1
tmp(1:N)=tmp(1:N)+K(i,1:N)*a(j,i)
enddo
do i=1,N
K(j,i)=h*func(N,tx,tmp,i,ik)
enddo
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i)+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R)/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err)then
x=x+h
do i=1,s
y(1:N)=y(1:N)+b1(i)*K(i,1:N)
enddo
FLAG=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
enddo
return
end subroutine rkf451
subroutine rkf451_e(func,x,y,xbound,info,tol,ik)
!sikinote
! propagate from y(x) to y(xbound) without interval
!
! info = -1 : h < hmin. Maybe path the singular point.
! = 1 : x reach xbound.
!
implicit none
interface
function func(iN,ix,iy,is,iik)
implicit none
integer,intent(in)::iN,is,iik
double precision,intent(in)::ix,iy(1:iN)
double precision::func
end function func
end interface
integer::N,ik
double precision,intent(in)::xbound,tol
double precision,intent(inout)::x,y(:)
integer,intent(inout)::info
double precision,parameter::hmin=1d-14,hmax=1.d0
integer::i,j,FLAG,key,disc
double precision::R,delta,tx,Sy,err,h,h0
double precision,allocatable::tmp(:),K(:,:)
disc=0
key=0
h0=999d0
N=size(y,1)
allocate(tmp(1:N),K(1:s,1:N))
tmp=0d0; K=0d0
h=xbound-x
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
FLAG=1
if(abs(x-xbound).le.hmin*0.1d0)then
info=1
FLAG=0
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
tmp(1:N)=y(1:N)
do i=1,j-1
tmp(1:N)=tmp(1:N)+K(i,1:N)*a(j,i)
enddo
do i=1,N
K(j,i)=h*func(N,tx,tmp,i,ik)
enddo
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i)+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R)/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err.or.key.eq.1)then
x=x+h
do i=1,s
y(1:N)=y(1:N)+b1(i)*K(i,1:N)
enddo
key=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
disc=1
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
enddo
if(disc.eq.1)then
info=-1
endif
deallocate(tmp,K)
return
end subroutine rkf451_e
end module RKmod
!--------------------
subroutine seeklm(xa,xb,za,zb,nodes,poles,r0,v0,omg0,u0,ik)
!nodes --> number of nodes
!poles --> number of local maximam/minimam
!
!nodes=0
!
!
! x--------------------------------
! \_______
! \______
! \
! orbit of bullet
!
!nodes=1
! za_____________xa
! __/\_
! ________/ \_
! / \
! x------------------\------------
! \
! \
! \
! \orbit of bullet
!
!nodes=2
!
! zb________________ xb
! /\
! xa / \
! x-----------/--------\------------
! \ / \
! \ / \
! za______\/ \
! \orbit of bullet
!
use RKmod
use GBL
implicit none
integer,intent(in)::ik
double precision,intent(in)::omg0(1:3),r0(1:3),v0(1:3),u0(1:3)
double precision,intent(out)::xa,xb,za,zb
integer,intent(out)::nodes,poles
integer::i,j,info
integer,parameter::N=12
double precision::vz0,vz1,vz2,t0,t1,t2,ta,tb,tbef,rz0,rz1
double precision::x(1:N),tt,th,tx(1:N),bt,bh,bx(1:N)
double precision::t,h,xbound,rkfd
external::rkfd
x(1:3)=r0(1:3)
x(4:6)=v0(1:3)
x(7:9)=omg0(1:3)
x(10:12)=u0(1:3)
xbound=10d0
i=1; t=0d0; h=1d-1; info=0
info=0; nodes=0; poles=0
xa=0d0; xb=0d0; za=0d0; zb=0d0
call rk_preparation("rkf45")
do while(info.eq.0)
tt=t; th=h; tx=x
rz0=x(3); vz0=x(6); t0=t
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
rz1=x(3); vz1=x(6); t1=t
if(vz0*vz1.lt.0.d0)then
bt=tt; bh=th; bx=tx
t0=bt; t2=0.5d0*(2d0*bt+th); t1=bt+th
do j=1,60
tt=bt; th=bh; tx=bx
th=t2-bt
call rkf451(rkfd,size(tx),tt,th,tx,xbound,info,tol,ik)
vz2=tx(6)
if(vz2*vz0.ge.0.d0)then
t2=t2+0.5d0*(t1-t2)
else
tbef=t2
t2=t2-0.5d0*(t1-t2)
t1=tbef
endif
if(abs(t1-t2)/t1.lt.1d-10)then
if(poles.eq.0)then
ta=t2; xa=tx(1); za=tx(3)
else
tb=t2; xb=tx(1); zb=tx(3)
endif
exit
endif
enddo
poles=poles+1
endif
if((rz0-r0(3))*(rz1-r0(3)).lt.0d0)then
nodes=nodes+1
endif
if(x(3).lt.0d0)then
info=1
endif
i=i+1
enddo
call rk_deallocation("rkf45")
return
end subroutine seeklm
subroutine seekzeroin(xa,xb,nodes,r0,v0,omg0,u0,ik)
!nodes --> number of nodes
!
!nodes=0
!
!
! x--------------------------------
! \_______
! \______
! \
! orbit of bullet
!
!nodes=1
!
! __/\_
! ________/ \_
! / \ xa
! x------------------\------------
! \
! \
! \
! \orbit of bullet
!
!nodes=2
!
!
! /\
! xa / \ xb
! x-----------/--------\------------
! \ / \
! \ / \
! \/ \
! \orbit of bullet
!
use RKmod
use GBL
implicit none
integer,intent(in)::ik
double precision,intent(in)::omg0(1:3),r0(1:3),v0(1:3),u0(1:3)
double precision,intent(out)::xa,xb
integer,intent(out)::nodes
integer::i,j,info
integer,parameter::N=12
double precision::rz0,rz1,rz2,t0,t1,t2,ta,tb,tbef,rzini
double precision::x(1:N),tt,th,tx(1:N),bt,bh,bx(1:N)
double precision::t,h,xbound,rkfd
external::rkfd
rzini=r0(3)
x(1:3)=r0(1:3)
x(4:6)=v0(1:3)
x(7:9)=omg0(1:3)
x(10:12)=u0(1:3)
xbound=10d0
i=1; t=0d0; h=1d-1; info=0
info=0; nodes=0
xa=0d0; xb=0d0
call rk_preparation("rkf45")
!-----1step-----
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
!----------------
do while(info.eq.0)
tt=t; th=h; tx=x
rz0=x(3); t0=t
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
rz1=x(3); t1=t
if(rz0-rzini.lt.0.d0.neqv.rz1-rzini.lt.0.d0)then
bt=tt; bh=th; bx=tx
t0=bt; t2=0.5d0*(2d0*bt+th); t1=bt+th
do j=1,60
tt=bt; th=bh; tx=bx
th=t2-bt
call rkf451(rkfd,size(tx),tt,th,tx,xbound,info,tol,ik)
rz2=tx(3)
if(rz2-rzini.lt.0.d0.eqv.rz0-rzini.lt.0.d0)then
t2=t2+0.5d0*(t1-t2)
else
tbef=t2
t2=t2-0.5d0*(t1-t2)
t1=tbef
endif
if(abs(t1-t2)/t1.lt.1d-10)then
if(nodes.eq.0)then
ta=t2; xa=tx(1)
else
tb=t2; xb=tx(1)
endif
nodes=nodes+1
exit
endif
enddo
endif
if(x(3).lt.0d0)then
info=1
endif
i=i+1
enddo
call rk_deallocation("rkf45")
return
end subroutine seekzeroin
subroutine detwy(energy,r,vy,omgx,omgz,u,zeroinx,exwy,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,zeroinx
double precision,intent(in)::r(1:3),omgx,omgz,u(1:3),vy
double precision,intent(out)::exwy,exvz
integer::Nr,count,Nsplit
double precision,parameter::pi=dacos(-1d0)
double precision,allocatable::rd(:)
double precision::ad,bd,wycond
external::wycond
ad=-800d0*2d0*pi; bd=2d0*pi; Nsplit=25; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond,energy,r,vy,omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,"bisection",1)
exwy=rd(1)
if(ik.eq.0)then
ad=exwy-5d0*2d0*pi; bd=exwy+5d0*2d0*pi; Nsplit=1; Nr=1
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond,energy,r,vy,omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,"false_position",0)
exwy=rd(1)
endif
deallocate(rd)
return
end subroutine detwy
!--------------------------
function wycond(energy,r,vy,omgx,omgy,omgz,u,zeroinx,exvz,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),u(1:3),vy,omgx,omgy,omgz,zeroinx
double precision,intent(out)::exvz
integer::nodes
double precision::zeroinx1,zeroinx2,wycond,v(1:3),omg(1:3)
omg(1)=omgx; omg(2)=omgy; omg(3)=omgz
call detvz(energy,r,vy,omg,u,exvz,ik)
v(1)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
v(2)=vy
v(3)=exvz
call seekzeroin(zeroinx1,zeroinx2,nodes,r,v,omg,u,ik)
if(zeroinx2.ge.1d-10)then
wycond=zeroinx2-zeroinx
else
wycond=2d0*zeroinx
endif
return
end function wycond
!------------------------------
subroutine detwy2(energy,r,vy,omgx,omgz,u,udh,exwy,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,udh,r(1:3),omgx,omgz,u(1:3),vy
double precision,intent(out)::exwy,exvz
integer::Nr,count,Nsplit
double precision,parameter::pi=dacos(-1d0)
double precision,allocatable::rd(:)
double precision::ad,bd,wycond2
external::wycond2
ad=-1000d0*2d0*pi; bd=2d0*pi; Nsplit=25; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond2,energy,r,vy,omgx,omgz,u,udh,ad,bd,Nsplit,Nr,rd,exvz,count,"bisection",1)
exwy=rd(1)
if(ik.eq.0)then
ad=exwy-5d0*2d0*pi; bd=exwy+5d0*2d0*pi; Nsplit=1; Nr=1
count=0; rd(1:Nr)=0d0
call rootfindingw(wycond2,energy,r,vy,omgx,omgz,u,udh,ad,bd,Nsplit,Nr,rd,exvz,count,"false_position",0)
exwy=rd(1)
endif
deallocate(rd)
return
end subroutine detwy2
!--------------------------
function wycond2(energy,r,vy,omgx,omgy,omgz,u,udh,exvz,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),u(1:3),vy,omgx,omgy,omgz,udh
double precision,intent(out)::exvz
integer::nodes,poles
double precision::xa,xb,za,zb,z0,wycond2,v(1:3),omg(1:3)
omg(1)=omgx; omg(2)=omgy; omg(3)=omgz
call detvz(energy,r,vy,omg,u,exvz,ik)
v(1)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
v(2)=vy
v(3)=exvz
z0=r(3)
call seeklm(xa,xb,za,zb,nodes,poles,r,v,omg,u,ik)
if(poles.eq.0.or.za.lt.0d0)then
wycond2=10d0
elseif(poles.eq.1)then
wycond2=za-z0
elseif(poles.eq.2)then
wycond2=zb-za
else
write(6,*)"unknown,poles-->",poles
stop
endif
wycond2=wycond2-udh
return
end function wycond2
!-------------------------
subroutine detvz(energy,r,vy,omg,u,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy
double precision,intent(in)::r(1:3),omg(1:3),u(1:3),vy
integer::Nr,count,Nsplit
double precision,intent(out)::exvz
double precision,allocatable::rd(:)
double precision::ad,bd,vzcond
external::vzcond
ad=-30d0; bd=1d0; Nsplit=80; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call vzroot(vzcond,energy,r,vy,omg,u,ad,bd,Nsplit,Nr,rd,count,ik)
exvz=rd(1)
return
end subroutine detvz
!------------------------
function vzcond(energy,r,vy,vz,omg,u,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),vy,vz,omg(1:3),u(1:3)
double precision::vzcond,v(1:3)
integer::nodes,poles
double precision::xa,xb,za,zb,z0
v(1)=dsqrt((2d0*energy/m)-vz**2-vy**2)
v(2)=vy
v(3)=vz
z0=r(3)
call seeklm(xa,xb,za,zb,nodes,poles,r,v,omg,u,ik)
if(poles.eq.0)then
vzcond=-z0-1d0
elseif(poles.eq.1)then
vzcond=za-z0
elseif(poles.eq.2)then
vzcond=za+zb-2d0*z0
else
write(6,*)"unknown,poles-->",poles
stop
endif
return
end function vzcond
!--------------------
subroutine vzroot(func,energy,r,vy,omg,u,ad,bd,Nsplit,Nr,rd,count,ik)
!Developer : sikino
use GBL
implicit none
interface
function func(ienergy,ir,ivy,ivz,iomg,iu,iik)
implicit none
integer,intent(in)::iik
double precision,intent(in)::ienergy,ir(1:3),ivy,ivz,iomg(1:3),iu(1:3)
double precision::func
end function func
end interface
integer,intent(in)::Nr,Nsplit,ik
double precision,intent(in)::ad,bd,energy,r(1:3),vy,omg(1:3),u(1:3)
integer,intent(out)::count
double precision,intent(out)::rd(1:Nr)
integer::N,i,j
double precision::h,hd,x0,x1,x2,y0,y1,y2,Dy0,tx1,ty1
!ad < bd
if(ad.ge.bd)then
write(6,'(A,2e15.6e3)')"must be ad < bd, your ad,bd --> ",ad,bd
write(6,'(A)')"program stop at rootfinding"
stop
end if
N=Nsplit
hd=abs(ad-bd)/dble(N)
count=0
x0=ad
y0=func(energy,r,vy,x0,omg,u,ik)
do i=1,N
x1=x0+hd
y1=func(energy,r,vy,x1,omg,u,ik)
if(y0.lt.0.d0.neqv.y1.lt.0.d0)then
tx1=x1
ty1=y1
!bisection rule
do j=1,60
x2=0.5d0*(x0+x1)
y2=func(energy,r,vy,x2,omg,u,ik)
if(y2.lt.0.d0.eqv.y0.lt.0.d0)then
x0=x2
else
x1=x2
endif
if(abs((x1-x0)/x2).lt.eps)then
if(y2.le.1d0)then
count=count+1
rd(count)=x2
exit
endif
endif
enddo
if(j.eq.61)write(6,*)"+--cannot convergence at root-finding method bs--+"
if(count.ge.Nr)exit
x1=tx1
y1=ty1
endif
x0=x1
y0=y1
enddo
return
end subroutine vzroot
subroutine rootfindingw(func,energy,r,vy, &
omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,method,ik)
!Date : 2015/07/28
!Developer : sikino
use GBL
implicit none
interface
function func(ienergy,ir,ivy,iomgx,iomgy,iomgz,iu,izin,iexvz,iik)
implicit none
integer,intent(in)::iik
double precision,intent(in)::ienergy,ir(1:3),ivy,iomgx,iomgy,iomgz,izin,iu(1:3)
double precision,intent(out)::iexvz
double precision::func
end function func
end interface
integer,intent(in)::Nr,Nsplit,ik
double precision,intent(in)::ad,bd,energy,r(1:3),vy,u(1:3)
double precision,intent(in)::omgx,omgz,zeroinx
integer,intent(out)::count
double precision,intent(out)::rd(1:Nr),exvz
double precision,parameter::pi=dacos(-1d0)
character(*),intent(in)::method
integer::N,i,j
double precision::h,hd,x0,x1,x2,y0,y1,y2,Dy0,tx1,ty1
!ad < bd
if(ad.ge.bd)then
write(6,'(A,2e15.6e3)')"must be ad < bd, your ad,bd --> ",ad,bd
write(6,'(A)')"program stop at rootfinding"
stop
end if
!Announsment
write(6,'(A,A)')" ---- ",trim(method)
N=Nsplit
hd=abs(ad-bd)/dble(N)
count=0
x0=ad
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
do i=1,N
x1=x0+hd
y1=func(energy,r,vy,omgx,x1,omgz,u,zeroinx,exvz,ik)
write(6,'(A,i0,A,i0,A,f14.8,A,f14.8)')" Sequence ",i," of ",N," : omgy/2pi ",x1/2d0/pi, " : zeroin ",y1
if(y0.lt.0.d0.neqv.y1.lt.0.d0)then
write(6,'(A)')" +--- Root find, go to conversion phase --+ "
tx1=x1
ty1=y1
if(trim(method).eq."bisection")then
!bisection rule
do j=1,60
x2=0.5d0*(x0+x1)
y2=func(energy,r,vy,omgx,x2,omgz,u,zeroinx,exvz,ik)
if(y2.lt.0.d0.eqv.y0.lt.0.d0)then
x0=x2
else
x1=x2
endif
write(6,'(A,f16.8,A)')"Conversion => ",eps*abs(x2/(x1-x0))*100d0,"%"
if(abs((x1-x0)/x2).lt.eps)then
!If y2 is large, y2 is singular point.
if(y2.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
enddo
if(j.eq.60)write(6,*)"+--cannot convergence at root-finding method bs--+"
elseif(trim(method).eq."newton_raphson")then
!Newton-Raphson method
do j=1,10
h=1.d-4
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
Dy0=(func(energy,r,vy,omgx,x0+h,omgz,u,zeroinx,exvz,ik)-y0)/h
x2=x0-y0/Dy0
if(abs((x0-x2)/x2).lt.eps)then
if(y0.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
x0=x2
enddo
if(j.eq.10)write(6,*)"+--cannot convergence at root-finding method nr--+"
elseif(trim(method).eq."false_position")then
!false position method
if(abs(y1).gt.abs(y0))then
do j=1,30
x2=x0-y0*(x1-x0)/(y1-y0)
write(6,'(A,f16.8,A)')"Conversion => ",eps*abs(x2/(x2-x0))*100d0,"%"
if(abs((x2-x0)/x2).lt.eps)then
if(y0.le.1d0)then
count=count+1
rd(count)=x2
end if
exit
endif
x0=x2
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
enddo
else
do j=1,30
x2=x0-y0*(x1-x0)/(y1-y0)
write(6,'(A,f15.8,A)')"Conversion => ",eps*abs(x2/(x1-x2))*100d0,"%"
if(abs((x2-x1)/x2).lt.eps)then
if(y1.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
x1=x2
y1=func(energy,r,vy,omgx,x1,omgz,u,zeroinx,exvz,ik)
enddo
endif
if(j.eq.30)write(6,*)"+--cannot convergence at root-finding method fp--+"
else
write(6,'(A,A)')"unknown type of method, your method--> ",trim(method)
write(6,'(A,A)')"program stop"
stop
end if
if(count.ge.Nr)exit
x1=tx1
y1=ty1
endif
x0=x1
y0=y1
enddo
return
end subroutine rootfindingw
!---------------------------
function rkfd(N,t,x,s,ik)
use GBL
implicit none
integer,intent(in)::N,s,ik
double precision,intent(in)::t,x(1:N)
double precision::r(1:3),v(1:3),relv(1:3),omg(1:3),u(1:3),nw,nv,I
double precision::rkfd,gravity,vis1,vis2,mag,Nz,Nze
double precision,parameter::pi=datan(1d0)*4d0
external::gravity,vis1,vis2,mag,Nz,Nze
r(1:3)=x(1:3)
v(1:3)=x(4:6)
omg(1:3)=x(7:9)
u(1:3)=x(10:12)
relv(1:3)=v(1:3)-u(1:3)
rkfd=0.d0
if(s.le.3)then
! Differential equation of position
! d {x,y,z}/dt = v{x,y,z}
rkfd=v(s)
elseif(s.le.6)then
! Differential equation of velocity
! d v_{x,y,z}/dt = F{x,y,z}
rkfd=gravity(s-3,m,g,r)+vis1(s-3,relv,a,eta) &
+vis2(s-3,relv,a,eta,rho)+mag(s-3,omg,relv,a,rho)
rkfd=rkfd/m
elseif(s.le.9)then
! Differential equation for omega
! d omega{x,y,z}/dt = N_{x,y,z}/I
if(trim(omgdecay).eq."yes")then
I=0.4d0*m*a*a
nv=dsqrt(relv(1)**2+relv(2)**2+relv(3)**2)
nw=dsqrt(omg(1)**2+omg(2)**2+omg(3)**2)
if(nw.le.1d-13)then
rkfd=0d0
else
if(ik.eq.0)then
rkfd=(Nz(nv,a,eta,rho,nw)/I)*x(s)/nw
else
rkfd=(Nze(nv,a,eta,rho,nw)/I)*x(s)/nw
end if
endif
else
rkfd=0d0
endif
else
! Differential equation for wind
! d u{x,y,z}/dt = Fu_{x,y,z}
rkfd=0d0
endif
return
end function rkfd
!-----------------------------
function gravity(dir,m,g,r)
implicit none
integer,intent(in)::dir
double precision::gravity
double precision,intent(in)::m,g,r(1:3)
if(dir.eq.3)then
gravity=-m*g
else
gravity=0.d0
endif
return
end function gravity
!-------------------------------
function c1(a,eta)
implicit none
double precision::c1
double precision,intent(in)::eta,a
double precision,parameter::pi=dacos(-1.d0)
c1=6.d0*pi*eta*a
return
end function c1
!------------------------------
function c2(nv,a,eta,rho)
implicit none
double precision,parameter::pi=dacos(-1.d0)
double precision,intent(in)::nv,eta,a,rho
double precision::Cd,Reynolds,c2
external::Cd,Reynolds
c2=0.5d0*Cd(Reynolds(nv,a,eta,rho))*rho*pi*a*a
return
end function c2
!-----------------------------
function vis1(dir,v,a,eta)
implicit none
integer,intent(in)::dir
double precision,intent(in)::v(1:3),a,eta
double precision::vis1,norm,nv,c1
external::c1
nv=dsqrt(v(1)**2.d0+v(2)**2.d0+v(3)**2.d0)
norm=c1(a,eta)*nv
vis1=-norm*v(dir)/nv
return
end function vis1
!-------------------------
function vis2(dir,v,a,eta,rho)
implicit none
integer,intent(in)::dir
double precision,intent(in)::v(1:3),a,eta,rho
double precision::vis2,norm,nv,c2
external::c2
nv=dsqrt(v(1)*v(1)+v(2)*v(2)+v(3)*v(3))
norm=c2(nv,a,eta,rho)*nv*nv
vis2=-norm*v(dir)/nv
return
end function vis2
!--------------------------
function mag(dir,omg,v,a,rho)
implicit none
integer,intent(in)::dir
double precision,intent(in)::omg(1:3),v(1:3),a,rho
double precision,parameter::pi=dacos(-1.d0)
double precision::mag,L(1:3),nomg,nv,nL,Cl
nomg=dsqrt(omg(1)*omg(1)+omg(2)*omg(2)+omg(3)*omg(3))
if(nomg.le.1.d-14)then
mag=0.d0
return
endif
nv=dsqrt(v(1)*v(1)+v(2)*v(2)+v(3)*v(3))
L(1)=v(2)*omg(3)-v(3)*omg(2)
L(2)=v(3)*omg(1)-v(1)*omg(3)
L(3)=v(1)*omg(2)-v(2)*omg(1)
nL=dsqrt(L(1)*L(1)+L(2)*L(2)+L(3)*L(3))
if(nL.le.1.d-14)then
mag=0.d0
return
endif
! for BB bullet
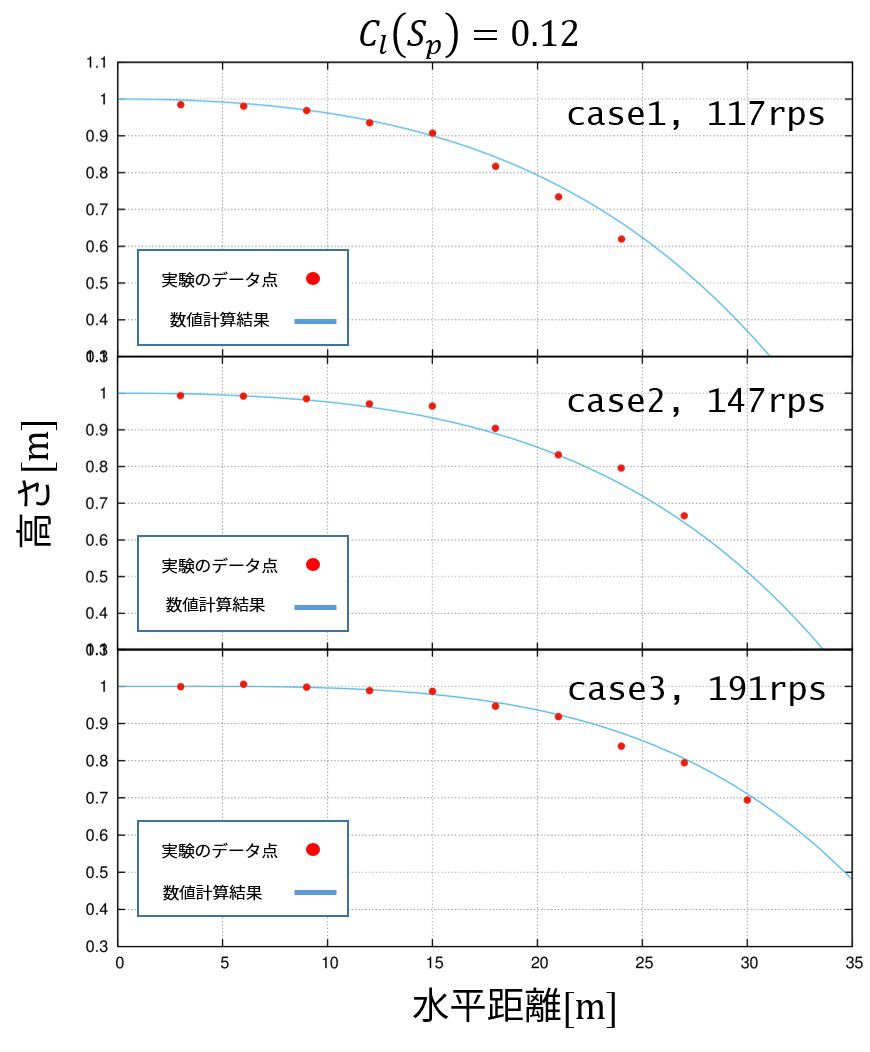
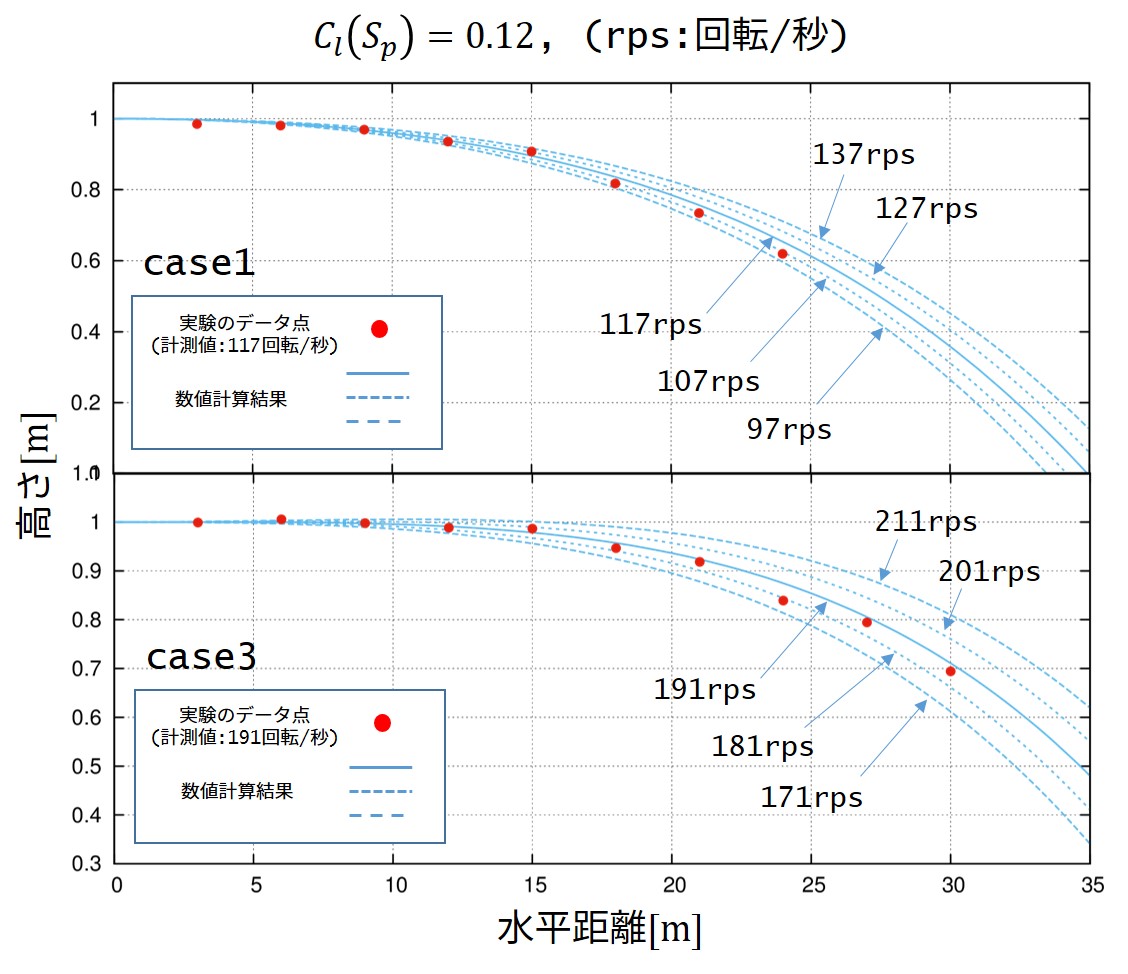
Cl=0.12d0
mag=-Cl*(4.d0/3.d0)*pi*(a**3d0)*2.d0*rho*nomg*nv*L(dir)/nL
return
end function mag
!--------------------------
function Reynolds(nv,a,eta,rho)
!Reynolds number
! nv : norm of velocity of object
! a : radius of object
!eta : viscosity (not Kinetic viscosity)
!rho : density of fluid
implicit none
double precision,intent(in)::nv,a,eta,rho
double precision::keta,Reynolds
!keta means Kinetic viscosity
keta=eta/rho
Reynolds=nv*2.d0*a/keta
return
end function Reynolds
!---------------------------
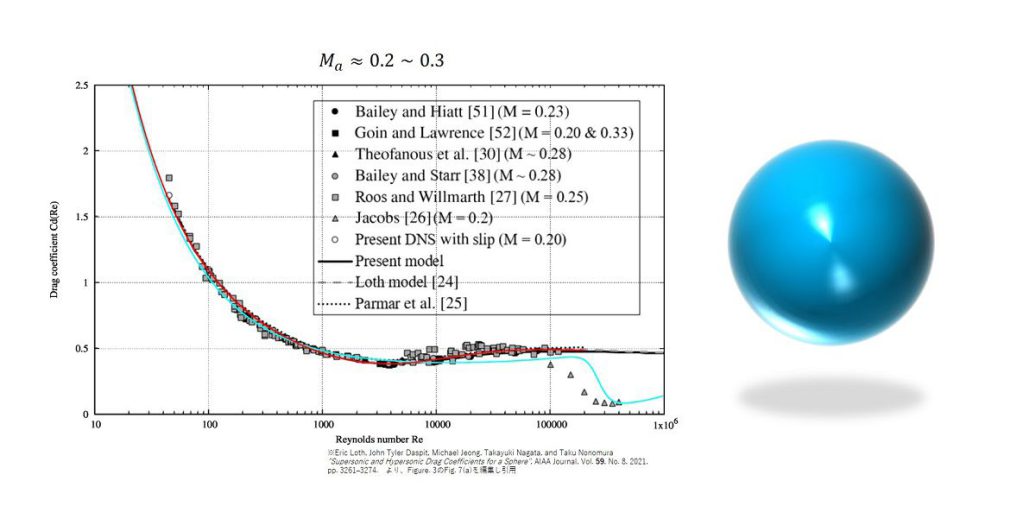
function Cd(Re)
!From
!http://www.chem.mtu.edu/~fmorriso/DataCorrelationForSphereDrag2013.pdf
!Drag coefficient Cd,
!Cd depend on Reynolds number,Re.
!Fource of Drug,D is written by
! 1
! D= ---Cd*rho*pi*a**2*|V|**2
! 2
! ^ This Cd!
implicit none
double precision,intent(in)::Re
double precision::Cd,c1,c2,c3,c4
c1=24.d0/Re
c2=Re/5.d0
c2=2.6d0*c2/(1.d0+c2**(1.52d0))
c3=Re/263000d0
c3=0.411d0*c3**(-7.94d0)/(1.d0+c3**(-8d0))
c4=Re**0.8d0/461000d0
Cd=c1+c2+c3+c4
return
end function Cd
!----------------------------
function Nz(nv,a,eta,rho,omg)
!Moment of omg direction
implicit none
double precision,intent(in)::nv,a,eta,rho,omg
double precision::Nz,Cf,Fintegral
external::Cf,Fintegral
Nz=0.5d0*rho*Cf(nv,a,eta,rho)*a**3
Nz=Nz*Fintegral(nv,a,omg)
return
end function Nz
function Nze(nv,a,eta,rho,omg)
implicit none
double precision,intent(in)::nv,a,eta,rho,omg
double precision::Nze,Cf,Fintegral
double precision,parameter::pi=atan(1d0)*4d0
external::Cf,Fintegral
double precision::pc,tc,vu,vd,t
pc=pi/5.32065d0 ! magic phi
tc=pi/3.60475d0 ! magic theta
vu= nv*sin(pc)-a*omg*sin(tc)
vd=-nv*sin(pc)-a*omg*sin(tc)
Nze=-0.5d0*rho*Cf(nv,a,eta,rho)
Nze=Nze*(4d0*pi*a**2)*a*0.5d0
Nze=-Nze*(abs(vu)*vu+abs(vd)*vd)
return
end function Nze
!-------------------
function Cf(nv,a,eta,rho)
implicit none
! nv : norm of velocity of object
! a : radius of object
!eta : viscosity (not Kinetic viscosity)
!rho : density of fluid
double precision,intent(in)::nv,a,eta,rho
double precision::Reynolds,Cf
external::Reynolds
! Laminar flow
Cf=1.328d0/dsqrt(Reynolds(nv,a,eta,rho))
! Turbulent flow Re > 10^7
!Cf=0.455d0/(log10(Reynolds(nv,a,eta,rho))**(2.58d0))
return
end function Cf
!----------------------------------
function Fintegral(u,R,omega)
! 2016/07/23
! 2pi pi
! / /
! | dphi | |u*sin(phi)-R*omega*sin(theta)|*{u*sin(phi)-R*omega*sin(theta)}*sin^2(theta) d theta
! / /
! 0 0
implicit none
double precision,intent(in)::u,R,omega
double precision,parameter::pi=datan(1.d0)*4d0
double precision::Fintegral,s,Fphi,x(1:15),w(1:15)
external::Fphi
integer::i
s=0d0
call GaussKronrod15ab(0d0,pi,x,w)
do i=1,15
s=s+w(i)*Fphi(u,R,omega,x(i))
enddo
call GaussKronrod15ab(pi,2d0*pi,x,w)
do i=1,15
s=s+w(i)*Fphi(u,R,omega,x(i))
enddo
Fintegral=s
return
end function Fintegral
!------------------------------
subroutine GaussKronrod15ab(a,b,x,w)
!Gauss-Kronrod Quadrature Nodes and Weights
!http://www.advanpix.com/2011/11/07/gauss-kronrod-quadrature-nodes-weights/
implicit none
double precision,intent(in)::a,b
double precision,intent(out)::x(1:15),w(1:15)
integer::i
integer,parameter::N=15
x=0d0; w=0d0
x( 8) = 0d0
x( 9) = 2.077849550078984676006894037732449d-1
x(10) = 4.058451513773971669066064120769615d-1
x(11) = 5.860872354676911302941448382587296d-1
x(12) = 7.415311855993944398638647732807884d-1
x(13) = 8.648644233597690727897127886409262d-1
x(14) = 9.491079123427585245261896840478513d-1
x(15) = 9.914553711208126392068546975263285d-1
do i=1,7
x(i)=-x(N-i+1)
enddo
w( 8) = 2.094821410847278280129991748917143d-1
w( 9) = 2.044329400752988924141619992346491d-1
w(10) = 1.903505780647854099132564024210137d-1
w(11) = 1.690047266392679028265834265985503d-1
w(12) = 1.406532597155259187451895905102379d-1
w(13) = 1.047900103222501838398763225415180d-1
w(14) = 6.309209262997855329070066318920429d-2
w(15) = 2.293532201052922496373200805896959d-2
do i=1,7
w(i)=w(N-i+1)
enddo
x=0.5d0*((b-a)*x+(a+b))
w=0.5d0*(b-a)*w
return
end subroutine GaussKronrod15ab
!----------------------------------------
function Fphi(u,R,omega,phi)
! using analysis solution.
!
! pi
! /
! | |u*sin(phi)-R*omega*sin(theta)|*{u*sin(phi)-R*omega*sin(theta)}*sin^2(theta) d theta
! /
! 0
!
implicit none
double precision,intent(in)::u,R,omega,phi
double precision,parameter::pi=dacos(-1d0)
double precision::a,b,c,tp,Fphi,Rw
a=(u/(R*omega))*sin(phi)
if(a.le.0d0)then
Fphi=-(0.5d0*a*a*pi-8d0*a/3d0+3d0*pi/8d0)
elseif(a.ge.1d0)then
Fphi=0.5d0*a*a*pi-8d0*a/3d0+3d0*pi/8d0
elseif(a.gt.0d0.and.a.lt.1d0)then
tp=asin(a)
b=-a*a*pi*0.5d0-8d0*a/3d0-3d0*pi/8d0+(2d0*a*a+3d0/2d0)*tp
c=-(a*a+1d0)*dsin(2d0*tp)+dsin(4d0*tp)/8d0+6d0*a*dcos(tp)-2d0*a*dcos(3d0*tp)/3d0
Fphi=b+c
else
write(6,*)"undefined at Fphi, program stop",a
stop
endif
Rw=R*omega
Fphi=Fphi*Rw*abs(Rw)
return
end function Fphi
!---------------------------------
subroutine bullet_orbit(N,x0,Nt,time,filename,ik)
!sikinote http://slpr.sakura.ne.jp/qp/
!Author : sikino
!Date : 2016/03/18 (yyyy/mm/dd)
! : 2016/03/20
use GBL
use RKmod
implicit none
integer,intent(in)::ik,N,Nt
double precision,intent(in)::x0(1:N),time(0:Nt)
character(*),intent(in)::filename
double precision,parameter::pi=datan(1d0)*4d0
integer::info,i,j
double precision::x(1:N),Ene,h,t,tbound,rkfd
external::rkfd
x=x0
info=0
t=time(0)
open(22,file=trim(filename),status='replace')
write(22,'(A,e12.5e1,A)')"# m: ",m,"[kg]"
write(22,'(A,f12.5,A)')"# g: ",g,"[m s^{-2}]"
write(22,'(A,e12.5e1,A)')"# a: ",a,"[m]"
write(22,'(A,f12.5,A)')"# temperature: ",temperature,"[degree Celsius]"
write(22,'(A,f12.5,A)')"# moisture: ",moisture,"[no-dimension]"
write(22,'(A,f12.5,A)')"# pressure: ",pressure,"[Pa]"
write(22,'(A,e12.5e1,A)')"# eta:",eta,"[kg m^{-1} s^{-1}]"
write(22,'(A,f12.5,A)')"# rho:",rho,"[kg m^{-3}]"
write(22,'(A,e12.5e1)')"# tol:",tol
write(22,'(A,e12.5e1)')"# eps:",eps
write(22,'(A,14A13)')"#","t[s]","x[m]","y[m]","z[m]","vx[m/s]","vy[m/s]","vz[m/s]" &
,"wx[rot/s]","wy[rot/s]","wz[rot/s]","windx[m/s]","windy[m/s]","windz[m/s]","Energy[J]"
Ene=0.5d0*m*(x(4)**2+x(5)**2+x(6)**2)
write(22,'(14f13.6)')t,(x(i),i=1,6),(x(i)/(2d0*pi),i=7,9),(x(i),i=10,12),Ene
call rk_preparation("rkf45")
do j=0,Nt-1
t=time(j); tbound=time(j+1); h=tbound-t
call rkf451_e(rkfd,t,x,tbound,info,tol,ik)
Ene=0.5d0*m*(x(4)**2+x(5)**2+x(6)**2)
write(22,'(14f13.6)')t,(x(i),i=1,6),(x(i)/(2d0*pi),i=7,9),(x(i),i=10,12),Ene
!Stop calculation when bullet reach ground.
if(x(3).lt.0d0)exit
enddo
call rk_deallocation("rkf45")
close(22)
write(6,'(A,e10.3)')"Reach ground at ",t
return
end subroutine bullet_orbit
program main
use GBL
implicit none
integer::i,N,Nt,ik
double precision,allocatable::x(:),time(:),r(:),u(:)
double precision,parameter::pi=datan(1d0)*4d0
double precision::rx,ry,rz,vx,vy,vz,ux,uy,uz,omgx,omgy,omgz
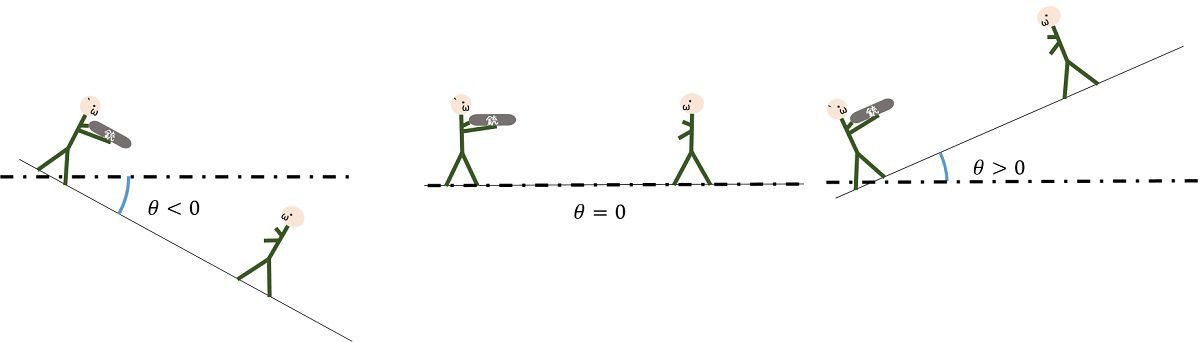
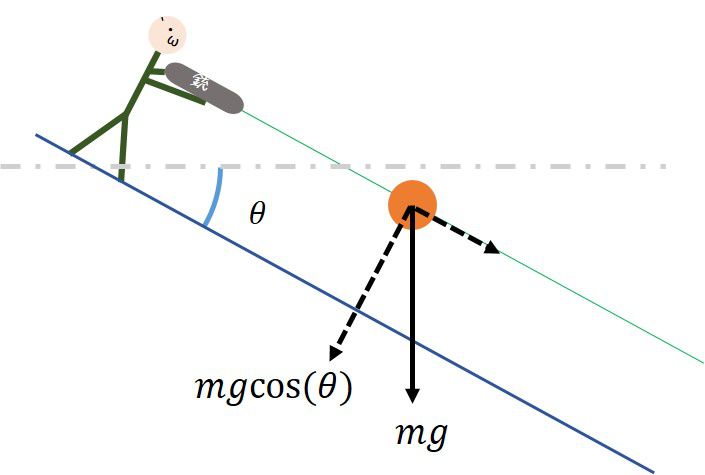
double precision::energy,zeroinx,updownz,stept,exvz,exwy,theta
character(48)::outputfile,filename,search_zeroin,search_updown
double precision::tbound
double precision::rho_humid,eta_air
double precision::r0(1:3),v0(1:3),omg0(1:3),u0(1:3)
external::rho_humid,eta_air
double precision::xa,xb,za,zb
integer::nodes,poles
real::t1,t0
namelist /input/m,a,energy,g,temperature,pressure,moisture &
,omgdecay,search_zeroin,zeroinx,search_updown,updownz &
,theta,rx,ry,rz,vy,ux,uy,uz,omgx,omgy,omgz &
,stept,outputfile,ik
open(10,file="./input")
read(10,nml=input)
close(10)
write(*,nml=input)
N=12
eta=eta_air(temperature)
rho=rho_humid(temperature,pressure,moisture)
vx=dsqrt((2d0*energy/m)-vy**2)*dcos(pi*theta/180d0)
vz=dsqrt((2d0*energy/m)-vy**2)*dsin(pi*theta/180d0)
omgx=omgx*2*pi
omgy=omgy*2*pi
omgz=omgz*2*pi
allocate(x(1:N))
x(1)=rx; x(4)=vx; x(7)=omgx; x(10)=ux
x(2)=ry; x(5)=vy; x(8)=omgy; x(11)=uy
x(3)=rz; x(6)=vz; x(9)=omgz; x(12)=uz
tbound=100d0
Nt=nint(tbound/stept)
allocate(time(0:Nt)); time=0d0
do i=0,Nt
time(i)=dble(i)*stept
enddo
filename=trim(outputfile)//".txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
call cpu_time(t0)
if(trim(search_zeroin).eq."yes")then
write(6,'(A)')"==============================="
write(6,'(A,f10.5)')" search vz and wy by zeroin --> ", zeroinx
allocate(r(1:3),u(1:3)); r(1:3)=x(1:3); u(1:3)=x(10:12)
call detwy(energy,r,x(5),x(7),x(9),u,zeroinx,exwy,exvz,ik)
write(6,*)exwy/(2d0*pi),exvz
x(4)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
x(5)=vy
x(6)=exvz
x(8)=exwy
filename=trim(outputfile)//"_opt.txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
deallocate(r,u)
endif
if(trim(search_updown).eq."yes")then
write(6,'(A)')"==============================="
write(6,'(A,f10.5)')" search vz and wy by up-down height --> ", updownz
allocate(r(1:3),u(1:3)); r(1:3)=x(1:3); u(1:3)=x(10:12)
call detwy2(energy,r,x(5),x(7),x(9),u,updownz,exwy,exvz,ik)
write(6,*)exwy/(2d0*pi),exvz
x(4)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
x(5)=vy
x(6)=exvz
x(8)=exwy
filename=trim(outputfile)//"_h.txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
deallocate(r,u)
endif
call cpu_time(t1)
write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"
stop
end program main