module DE_integration
!
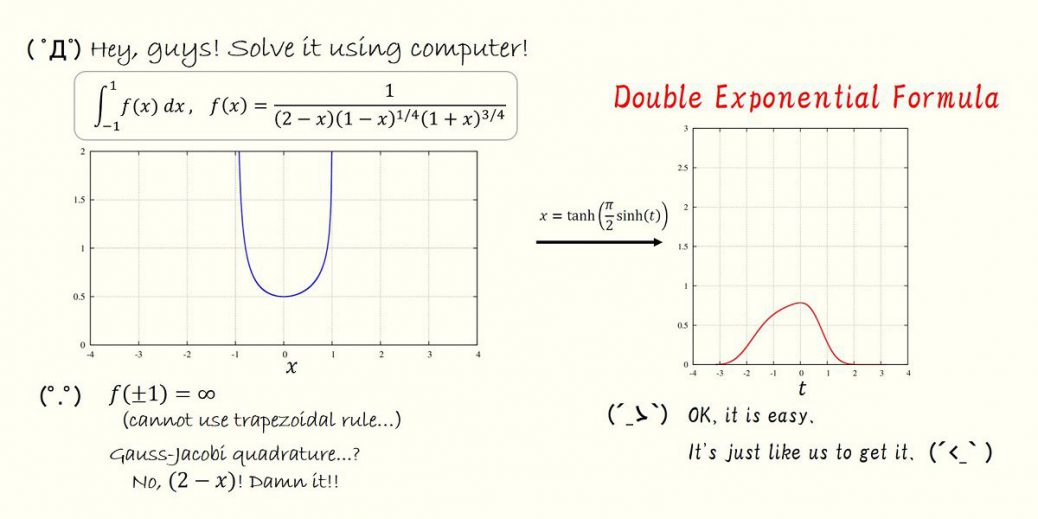
! Double Exponential (tanh-sinh) Formula
! for 1d, 2d, 3d.
!+------------------------------------+
! For 1 dimension integration
! call dde1d(f,a,b,eps,s,info)
! call cde1d(f,a,b,eps,s,info)
! call dde1d_hinf(f,a,eps,s,info)
! call cde1d_hinf(f,a,eps,s,info)
! call dde1d_ehinf(f,a,eps,s,info)
! call cde1d_ehinf(f,a,eps,s,info)
! call dde1d_inf(f,eps,s,info)
! call cde1d_inf(f,eps,s,info)
!
! call zde1d(f,a,b,eps,s,info)
! call zde1d_hinf(f,a,theta,eps,s,info)
! call zde1d_inf(f,a,theta,eps,s,info)
!
! d/cde1d, x:[a,b]
! [in] (dp/cp)f, (dp)a,b, (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde1d_hinf, x:[a,+infty]
! [in] (dp/cp)f, (dp)a, (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde1d_inf, x:[-infty,+infty]
! [in] (dp/cp)f, (dp)eps
! [out] (dp/cp)s, (int)info
!
! zde1d, x:[a,b]
! [in] (cp)f, (cp)a,b, (dp)eps
! [out] (cp)s, (int)info
!
! zde1d_hinf, x:[a,a+infty*e^{i*theta}]
! [in] (cp)f, (cp)a, (dp)eps, (dp)theta
! [out] (cp)s, (int)info
!
! zde1d_inf, x:[a-infty*e^{i*theta},a+infty*e^{i*theta}]
! [in] (cp)f, (cp)a, (dp)eps
! [out] (cp)s, (int)info
!
!+------------------------------------+
! For 2 dimension integration
! call dde2d(f,xa,xb,ya,yb,eps,s,info)
! call cde2d(f,xa,xb,ya,yb,eps,s,info)
! call dde2d_inf(f,eps,s,info)
! call cde2d_inf(f,eps,s,info)
!
! call dde_polar(f,eps,s,info)
! call cde_polar(f,eps,s,info)
!
! call zde2d(f,xa,xb,ya,yb,eps,s,info)
! call zde2d_inf(f,xa,thx,ya,thy,eps,s,info)
!
! d/cde2d, x:[xa,xb] y:[ya,yb]
! [in] (dp/cp)f, (dp)xa,xb,ya,yb, (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde2d_inf, x,y:[-infty,+infty]
! [in] (dp/cp)f, (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde_polar, r:[0,+infty], theta:[0,2*pi]
! [in] (dp/cp)f, (dp)eps
! [out] (dp/cp)s, (int)info
!
! zde2d, x:[xa,xb] y:[ya,yb]
! [in] (cp)f, (cp)xa,xb,ya,yb, (dp)eps
! [out] (cp)s, (int)info
!
! zde2d_inf, x:[xa-infty*e^{i*thx},xa+infty*e^{i*thx}]
! y:[ya-infty*e^{i*thy},ya+infty*e^{i*thy}]
! [in] (cp)f, (cp)xa,ya, (dp)thx,thy, (dp)eps
! [out] (cp)s, (int)info
!
!+------------------------------------+
! For 3 dimension integration
! call dde3d(f,xa,xb,ya,yb,za,zb,eps,s,info)
! call cde3d(f,xa,xb,ya,yb,za,zb,eps,s,info)
! call dde3d_inf(f,eps,s,info)
! call cde3d_inf(f,eps,s,info)
!
! call dde_spherical(f,eps,s,info)
! call cde_spherical(f,eps,s,info)
!
! call zde3d(f,xa,xb,ya,yb,za,zb,eps,s,info)
! call zde3d_inf(f,xa,thx,ya,thy,za,thz,eps,s,info)
!
! d/cde3d, x:[xa,xb] y:[ya,yb] z:[za,zb]
! [in] (dp/cp)f, (dp)xa,xb,ya,yb,za,zb (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde3d_inf, x,y,z:[-infty,+infty]
! [in] (dp/cp)f, (dp)eps
! [out] (dp/cp)s, (int)info
!
! d/cde_spherical, r:[0,+infty], theta:[0,pi], phi:[0,2*pi]
! [in] (dp/cp)f, (dp)eps
! [out] (dp/cp)s, (int)info
!
! zde3d, x:[xa,xb] y:[ya,yb] z:[za,zb]
! [in] (cp)f, (cp)xa,xb,ya,yb,za,zb (dp)eps
! [out] (cp)s, (int)info
!
! zde3d_inf, x:[xa-infty*e^{i*thx},xa+infty*e^{i*thx}]
! y:[ya-infty*e^{i*thy},ya+infty*e^{i*thy}]
! z:[za-infty*e^{i*thz},za+infty*e^{i*thz}]
! [in] (cp)f, (cp)xa,ya,za (dp)thx,thy,thz (dp)eps
! [out] (cp)s, (int)info
!
!+-------------------------------------+
! (dp) double precision
! (cp) complex(kind(0d0))
! (int) integer
!
! Output parameters
! s : integration result
! info : 0 --> relative error converge less than 'eps'.
! : 1 --> didn't converge in somewhere.
!
! http://slpr.sakura.ne.jp/qp
! 2016/12/17 (yyyy/mm/dd) by sikino
!
implicit none
integer,private,parameter::kmin=3
integer,private,parameter::kmax=14
! max order of DE integration
double precision,private,parameter::hr=6.d0 ! [-1,1]
double precision,private,parameter::hrhi=7.6d0 ! [ 0,\infty]
double precision,private,parameter::hrai=7.6d0 ! [-\infty,\infty]
double precision,private,parameter::c0=0.01d0 ! safe value for eps
double precision,private,parameter::pi2=1.5707963267948966d0
interface de1d
module procedure &
dde1d, &
cde1d
end interface de1d
interface de2d
module procedure &
dde2d, &
cde2d
end interface de2d
interface de3d
module procedure &
dde3d, &
cde3d
end interface de3d
interface de1d_hi
module procedure &
dde1d_hinf, &
cde1d_hinf
end interface de1d_hi
interface de1d_i
module procedure &
dde1d_inf, &
cde1d_inf
end interface de1d_i
interface de2d_i
module procedure &
dde2d_inf, &
cde2d_inf
end interface de2d_i
interface de3d_i
module procedure &
dde3d_inf, &
cde3d_inf
end interface de3d_i
contains
subroutine dde1d(f,a,b,eps,s,info)
implicit none
double precision,intent(in)::a,b,eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,mba,pba,err,seps
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(b-a)*0.5d0
pba=(b+a)*0.5d0
s0=f(pba)*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde1d
subroutine cde1d(f,a,b,eps,s,info)
implicit none
double precision,intent(in)::a,b,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,mba,pba,err,seps
complex(kind(0d0))::s0
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(b-a)*0.5d0
pba=(b+a)*0.5d0
s0=f(pba)*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde1d
subroutine zde1d(f,a,b,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,b
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=b-a
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
s0=f(a+re)*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(re*(xt+1d0)+a)*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde1d
subroutine dde2d(f,xa,xb,ya,yb,eps,s,info)
implicit none
double precision,intent(in)::xa,xb,ya,yb,eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
end function f
end interface
integer::j,nc,l
double precision::err,ft
double precision::h,s0,xt,wt,t,as,shk,mba,pba,seps
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(xb-xa)*0.5d0
pba=(xb+xa)*0.5d0
call dde2ds(f,ya,yb,pba,eps,ft,info)
s0=ft*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call dde2ds(f,ya,yb,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
err=abs(s-s0)/s0
if(l.eq.kmax+1)info=1
return
end subroutine dde2d
subroutine cde2d(f,xa,xb,ya,yb,eps,s,info)
implicit none
double precision,intent(in)::xa,xb,ya,yb,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::err
double precision::h,xt,wt,t,as,shk,mba,pba,seps
complex(kind(0d0))::s0,ft
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(xb-xa)*0.5d0
pba=(xb+xa)*0.5d0
call cde2ds(f,ya,yb,pba,eps,ft,info)
s0=ft*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call cde2ds(f,ya,yb,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
err=abs(s-s0)/s0
if(l.eq.kmax+1)info=1
return
end subroutine cde2d
subroutine zde2d(f,xa,xb,ya,yb,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::xa,xb,ya,yb
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w)
implicit none
complex(kind(0d0)),intent(in)::z,w
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re,ft
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=xb-xa
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
call zde2ds(f,ya,yb,xa+re,eps,ft,info)
s0=ft*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call zde2ds(f,ya,yb,re*(xt+1d0)+xa,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde2d
subroutine dde3d(f,xa,xb,ya,yb,za,zb,eps,s,info)
! Integrate for 3d
implicit none
double precision,intent(in)::xa,xb,ya,yb,za,zb,eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,ft,as,shk,mba,pba,err,seps
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(xb-xa)*0.5d0
pba=(xb+xa)*0.5d0
call dde3dsyz(f,ya,yb,za,zb,pba,eps,ft,info)
s0=ft*h*pi2*mba
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call dde3dsyz(f,ya,yb,za,zb,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde3d
subroutine cde3d(f,xa,xb,ya,yb,za,zb,eps,s,info)
! Integrate for 3d
implicit none
double precision,intent(in)::xa,xb,ya,yb,za,zb,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,mba,pba,err,seps
complex(kind(0d0))::s0,ft
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(xb-xa)*0.5d0
pba=(xb+xa)*0.5d0
call cde3dsyz(f,ya,yb,za,zb,pba,eps,ft,info)
s0=ft*h*pi2*mba
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call cde3dsyz(f,ya,yb,za,zb,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3d
subroutine zde3d(f,za,zb,wa,wb,va,vb,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::za,zb,wa,wb,va,vb
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re,ft
info=0
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=zb-za
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
call zde3dyzs(f,wa,wb,va,vb,za+re,eps,ft,info)
s0=ft*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call zde3dyzs(f,wa,wb,va,vb,re*(xt+1d0)+za,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3d
subroutine dde1d_hinf(f,a,eps,s,info)
implicit none
double precision,intent(in)::a,eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,err,esh,seps
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
s0=f(a+1d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
s=s+f(a+xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde1d_hinf
subroutine cde1d_hinf(f,a,eps,s,info)
implicit none
double precision,intent(in)::a,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,err,esh,seps
complex(kind(0d0))::s0
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
s0=f(a+1d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
s=s+f(a+xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde1d_hinf
subroutine zde1d_hinf(f,a,theta,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a
double precision,intent(in)::eps,theta
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,esh
complex(kind(0d0))::s0,eth
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*theta)
s0=f(a+eth)*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
s=s+f(a+xt*eth)*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde1d_hinf
subroutine dde1d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,err,seps
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde1d_inf
subroutine cde1d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x)
implicit none
double precision,intent(in)::x
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde1d_inf
subroutine zde1d_inf(f,a,theta,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a
double precision,intent(in)::theta,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*theta)
s0=f(a)*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(a+xt*eth)*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde1d_inf
subroutine zde2d_inf(f,xa,thx,ya,thy,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::xa,ya
double precision,intent(in)::thx,thy,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w)
implicit none
complex(kind(0d0)),intent(in)::z,w
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth,ft
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*thx)
call zde2ds_inf(f,ya,thy,xa,eps,ft,info)
s0=ft*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call zde2ds_inf(f,ya,thy,xa+xt*eth,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde2d_inf
subroutine dde2d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,ft,shk,err,seps
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
call dde2ds_inf(f,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call dde2ds_inf(f,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde2d_inf
subroutine cde2d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0,ft
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
call cde2ds_inf(f,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call cde2ds_inf(f,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde2d_inf
subroutine dde3d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,ft,shk,err,seps
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
call dde3dyzs_inf(f,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call dde3dyzs_inf(f,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde3d_inf
subroutine zde3d_inf(f,xa,thx,ya,thy,za,thz,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::xa,ya,za
double precision,intent(in)::thx,thy,thz,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth,ft
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*thx)
call zde3dyzs_inf(f,ya,thy,za,thz,xa,eps,ft,info)
s0=ft*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call zde3dyzs_inf(f,ya,thy,za,thz,xa+xt*eth,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3d_inf
subroutine cde3d_inf(f,eps,s,info)
implicit none
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0,ft
info=0
seps=c0*sqrt(eps)
h=hrai*0.5d0
call cde3dyzs_inf(f,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call cde3dyzs_inf(f,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3d_inf
subroutine dde_polar(f,eps,s,info)
implicit none
double precision,intent(in)::eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(r,th)
implicit none
double precision,intent(in)::r,th
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,ft,esh,err,seps
double precision,parameter::pipi=4d0*pi2
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
call dde2ds(f,0d0,pipi,1d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
call dde2ds(f,0d0,pipi,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde_polar
subroutine cde_polar(f,eps,s,info)
implicit none
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(r,th)
implicit none
double precision,intent(in)::r,th
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,esh
complex(kind(0d0))::s0,ft
double precision,parameter::pipi=4d0*pi2
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
call cde2ds(f,0d0,pipi,1d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
call cde2ds(f,0d0,pipi,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde_polar
subroutine dde_spherical(f,eps,s,info)
implicit none
double precision,intent(in)::eps
double precision,intent(out)::s
integer,intent(out)::info
interface
function f(r,th,phi)
implicit none
double precision,intent(in)::r,th,phi
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,ft,esh,err,seps
double precision,parameter::pi=2d0*pi2
double precision,parameter::pipi=4d0*pi2
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
call dde3dsyz(f,0d0,pi,0d0,pipi,1d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
call dde3dsyz(f,0d0,pi,0d0,pipi,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde_spherical
subroutine cde_spherical(f,eps,s,info)
implicit none
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(r,th,phi)
implicit none
double precision,intent(in)::r,th,phi
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,esh,err,seps
complex(kind(0d0))::s0,ft
double precision,parameter::pi=2d0*pi2
double precision,parameter::pipi=4d0*pi2
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
call cde3dsyz(f,0d0,pi,0d0,pipi,1d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
esh=exp(pi2*sinh(t))
xt=esh
wt=pi2*cosh(t)*esh
call cde3dsyz(f,0d0,pi,0d0,pipi,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde_spherical
!=================================
subroutine zde2ds(f,a,b,e,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,b,e
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(z,w)
implicit none
complex(kind(0d0)),intent(in)::z,w
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=b-a
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
s0=f(e,a+re)*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(e,re*(xt+1d0)+a)*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde2ds
subroutine zde3dyzs(f,a,b,va,vb,zc,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,b,zc,va,vb
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re,ft
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=b-a
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
call zde3dzs(f,va,vb,zc,a+re,eps,ft,info)
s0=ft*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call zde3dzs(f,va,vb,zc,re*(xt+1d0)+a,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3dyzs
subroutine zde3dzs(f,a,b,d,e,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,b,d,e
double precision,intent(in)::eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,rba,err,seps,xt,wt,shk,th,r
complex(kind(0d0))::s0,tz,eth,re
seps=c0*sqrt(eps)
h=hr*0.5d0
tz=b-a
r=abs(tz)
th=atan2(imag(tz),dble(tz))
eth=exp(dcmplx(0d0,1d0)*th)
rba=r*0.5d0
re=eth*rba
s0=f(d,e,a+re)*eth*h*pi2*rba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(d,e,re*(xt+1d0)+a)*wt
enddo
s=s0*0.5d0+s*h*re
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3dzs
!=================================
subroutine dde2ds_inf(f,e,eps,s,info)
implicit none
double precision,intent(in)::e,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,err,seps
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(e,0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(e,xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde2ds_inf
subroutine cde2ds_inf(f,e,eps,s,info)
implicit none
double precision,intent(in)::e,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(e,0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(e,xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde2ds_inf
subroutine dde2ds(f,a,b,e,eps,s,info)
! Integrate for 2d about y
implicit none
double precision,intent(in)::a,b,e,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,mba,pba,err,seps
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(b-a)*0.5d0
pba=(b+a)*0.5d0
s0=f(e,pba)*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(e,mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde2ds
subroutine cde2ds(f,a,b,e,eps,s,info)
! Integrate for 2d about y
implicit none
double precision,intent(in)::a,b,e,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y)
implicit none
double precision,intent(in)::x,y
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,mba,pba,err,seps
complex(kind(0d0))::s0
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(b-a)*0.5d0
pba=(b+a)*0.5d0
s0=f(e,pba)*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(e,mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde2ds
subroutine zde2ds_inf(f,a,theta,e,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,e
double precision,intent(in)::theta,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w)
implicit none
complex(kind(0d0)),intent(in)::z,w
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*theta)
s0=f(e,a)*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(e,a+xt*eth)*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde2ds_inf
subroutine zde3dyzs_inf(f,a,theta,za,thetaz,d,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,d,za
double precision,intent(in)::theta,thetaz,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth,ft
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*theta)
call zde3dzs_inf(f,za,thetaz,d,a,eps,ft,info)
s0=ft*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call zde3dzs_inf(f,za,thetaz,d,a+xt*eth,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3dyzs_inf
subroutine zde3dzs_inf(f,a,theta,d,e,eps,s,info)
implicit none
complex(kind(0d0)),intent(in)::a,d,e
double precision,intent(in)::theta,eps
complex(kind(0d0)),intent(out)::s
integer,intent(out)::info
interface
function f(z,w,v)
implicit none
complex(kind(0d0)),intent(in)::z,w,v
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,t,as,err,seps,xt,wt,shk
complex(kind(0d0))::s0,eth
info=0
seps=c0*sqrt(eps)
h=hrhi*0.5d0
eth=exp(dcmplx(0d0,1d0)*theta)
s0=f(d,e,a)*eth*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(d,e,a+xt*eth)*wt
enddo
s=s0*0.5d0+s*h*eth
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine zde3dzs_inf
subroutine dde3dyzs_inf(f,d,eps,s,info)
implicit none
double precision,intent(in)::d,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,ft,shk,err,seps
seps=c0*sqrt(eps)
h=hrai*0.5d0
call dde3dzs_inf(f,d,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call dde3dzs_inf(f,d,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde3dyzs_inf
subroutine dde3dzs_inf(f,d,e,eps,s,info)
implicit none
double precision,intent(in)::d,e,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,err,seps
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(d,e,0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(d,e,xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde3dzs_inf
subroutine cde3dyzs_inf(f,d,eps,s,info)
implicit none
double precision,intent(in)::d,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0,ft
seps=c0*sqrt(eps)
h=hrai*0.5d0
call cde3dzs_inf(f,d,0d0,eps,ft,info)
s0=ft*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
call cde3dzs_inf(f,d,xt,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3dyzs_inf
subroutine cde3dzs_inf(f,d,e,eps,s,info)
implicit none
double precision,intent(in)::d,e,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,err,seps
complex(kind(0d0))::s0
seps=c0*sqrt(eps)
h=hrai*0.5d0
s0=f(d,e,0d0)*h*pi2
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=sinh(shk)
wt=pi2*cosh(t)*cosh(shk)
s=s+f(d,e,xt)*wt
enddo
s=s0*0.5d0+s*h
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3dzs_inf
subroutine dde3dsyz(f,ya,yb,za,zb,xc,eps,s,info)
! Integrate for 3d about y,z
implicit none
double precision,intent(in)::ya,yb,za,zb,xc,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,ft,as,shk,mba,pba,err,seps
seps=c0*sqrt(eps)
h=hr*0.5d0
ft=0d0; s=0d0
mba=(yb-ya)*0.5d0
pba=(yb+ya)*0.5d0
call dde3dsz(f,za,zb,xc,pba,eps,ft,info)
s0=ft*h*pi2*mba
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call dde3dsz(f,za,zb,xc,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
return
end subroutine dde3dsyz
subroutine cde3dsyz(f,ya,yb,za,zb,xc,eps,s,info)
! Integrate for 3d about y,z
implicit none
double precision,intent(in)::ya,yb,za,zb,xc,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,mba,pba,err,seps
complex(kind(0d0))::s0,ft
seps=c0*sqrt(eps)
h=hr*0.5d0
ft=dcmplx(0d0,0d0); s=0d0
mba=(yb-ya)*0.5d0
pba=(yb+ya)*0.5d0
call cde3dsz(f,za,zb,xc,pba,eps,ft,info)
s0=ft*h*pi2*mba
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
call cde3dsz(f,za,zb,xc,mba*xt+pba,eps,ft,info)
s=s+ft*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3dsyz
subroutine dde3dsz(f,za,zb,xc,yc,eps,s,info)
! Integrate for 3d about z
implicit none
double precision,intent(in)::za,zb,xc,yc,eps
double precision,intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
double precision::f
end function f
end interface
integer::j,nc,l
double precision::h,s0,xt,wt,t,as,shk,mba,pba,err,seps
seps=c0*sqrt(eps)
h=hr*0.5d0
mba=(zb-za)*0.5d0
pba=(zb+za)*0.5d0
s0=f(xc,yc,pba)*h*pi2*mba
s=0d0
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(xc,yc,mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine dde3dsz
subroutine cde3dsz(f,za,zb,xc,yc,eps,s,info)
! Integrate for 3d about y,z
implicit none
double precision,intent(in)::za,zb,xc,yc,eps
complex(kind(0d0)),intent(out)::s
integer,intent(inout)::info
interface
function f(x,y,z)
implicit none
double precision,intent(in)::x,y,z
complex(kind(0d0))::f
end function f
end interface
integer::j,nc,l
double precision::h,xt,wt,t,as,shk,mba,pba,err,seps
complex(kind(0d0))::s0
seps=c0*sqrt(eps)
h=hr*0.5d0
s=0d0
mba=(zb-za)*0.5d0
pba=(zb+za)*0.5d0
s0=f(xc,yc,pba)*h*pi2*mba
nc=1
do l=2,kmax
s=0d0
nc=2*nc
h=h*0.5d0
do j=1,nc
t=dble(2*j-nc-1)*h
shk=pi2*sinh(t)
xt=tanh(shk)
wt=pi2*cosh(t)/(cosh(shk)*cosh(shk))
s=s+f(xc,yc,mba*xt+pba)*wt
enddo
s=s0*0.5d0+s*h*mba
as=abs(s); err=abs(s-s0)
if(as.ge.1d0)err=err/as
if(err.le.seps.and.l.ge.kmin)exit
s0=s
enddo
if(l.eq.kmax+1)info=1
return
end subroutine cde3dsz
end module DE_integration