微分方程式なら任せろーﾊﾞﾘﾊﾞﾘﾊﾞﾘｰ

• rk4のサブルーチン
• \(\displaystyle \frac{dy}{dx}=-y\sin{x}\)を解く
• \(
  \displaystyle \frac{d^2y}{dx^2}+2\gamma \frac{dy}{dx}+y=0
  \)を解く

ルンゲ=クッタ法ってもともとどういうもの？理論は？刻み幅\(h\)を自動的に制御する方法について知りたい方は、ルンゲ=クッタ法の系統的扱いと刻み幅制御へどうぞ。

4次ルンゲ=クッタ法は微分方程式を数値的に解く手段です。

ルンゲ=クッタ法が良く使われる理由は、ひとえにプログラムの実装のしやすさです。ルンゲクッタ法は非常に良い！というアルゴリズムではありませんが、他の方法よりもシンプルで、プログラムに組み込みやすいのです。

”4次”は問題の解の関数をテイラー展開した場合、4次までは一致するように作られた、という意味です。
例えば微分方程式
\(
\displaystyle \frac{dy}{dx}=g(x,y)
\)
を考えます。
数値計算では初期値(例えばx=0の時、y=1など)を決めて、そこからxをhだけ増やし、微分方程式というルールに従って関数\(y(0+h),y(0+h+h),y(0+h+h+h),\cdots\)を作り上げていきます。
この時、4次ルンゲ=クッタ法で求められる答えの関数というのは
\(
\displaystyle y(x+h)=y(x)+hg(x,y)+\frac{h^2}{2!}\frac{dg}{dx}+\frac{h^3}{3!}\frac{d^2g}{dx^2}+\frac{h^4}{4!}\frac{d^3g}{dx^3}+O(h^5)
\)
という関数になります。
\(
g(x,y)=-xy
\)
(ただし、初期条件\(x=0\)で\(y=1\))
である場合、微分方程式の解析解は
\(
\displaystyle y=e^{-x^2/2}
\)
であるため、4次ルンゲ=クッタ法によって導かれる答えは、
\(
\displaystyle y(x+h)=y(x)\left[1-hx+\frac{h^2}{2}(x^2-1)+\frac{h^3}{6}(-x^3+3x)+\frac{h^4}{24}(x^4-6x^2+3)\right]+O(h^5)
\)
となります。

本題に入りましょう。
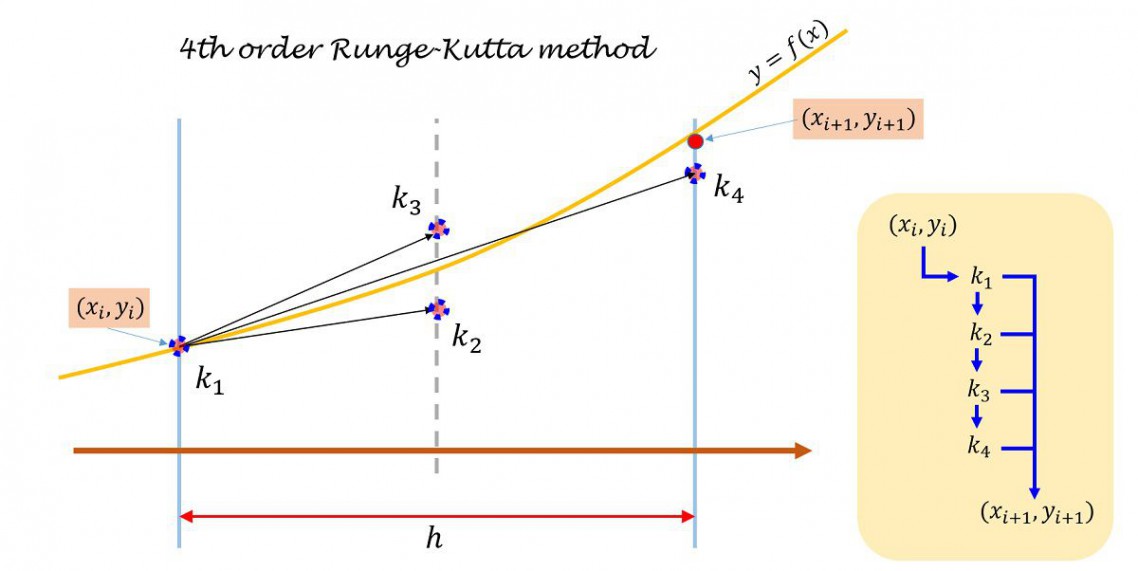
4次ルンゲ=クッタ法は6つのステップが必要となります。
初期値を\((x_0,y_0)\)と書くと、(\(y_0=y(x_0)\)です。)

1. \((x_0,y_0)\)より\(k_a\)を求める
2. \(k_a\)より\(k_b\)を求める
3. \(k_b\)より\(k_c\)を求める
4. \(k_c\)より\(k_d\)を求める
5. \(k_a,k_b,k_c,k_d\)より\(y(x_0+h)\)を求める
6. \((x_0+h,y(x_0+h))\)を初期値だと思って手順1に戻る。

という感じです。
３章：連立ルンゲ・クッタ法による微分方程式の解を参考にすると、数値計算での4次ルンゲ=クッタ法の計算スキームは以下のようになります。

解きたい微分方程式を連立１次微分方程式の形で書くと一般的にはこう書けます。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{dy_1}{dx} &= f_1(x,y_1,y_2,\cdots,y_N) \\
\frac{dy_2}{dx} &= f_2(x,y_1,y_2,\cdots,y_N) \\
&\vdots \\
\frac{dy_N}{dx} &= f_N(x,y_1,y_2,\cdots,y_N) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
まず係数\(k_a\)を求めます。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{a1} &= hf_1(x,y_1,y_2,\cdots,y_N) \\
k_{a2} &= hf_2(x,y_1,y_2,\cdots,y_N) \\
&\vdots \\
k_{aN} &= hf_N(x,y_1,y_2,\cdots,y_N) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
次に\(k_b\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{b1} &= hf_1(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
k_{b2} &= hf_2(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
&\vdots \\
k_{bN} &= hf_N(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
そして\(k_c\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{c1} &= hf_1(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
k_{c2} &= hf_2(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
&\vdots \\
k_{cN} &= hf_N(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
最後に\(k_d\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{d1} &= hf_1(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
k_{d2} &= hf_2(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
&\vdots \\
k_{dN} &= hf_N(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
最後に求めた\(k_a,k_b,k_c,k_d\)を使って\(x+h\)でのそれぞれの関数の値を導きます。、
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
x &= x+h \\
y_{1} &= y_{1}+(k_{a1}+2k_{b1}+2k_{c1}+k_{d1})/6 \\
y_{2} &= y_{2}+(k_{a2}+2k_{b2}+2k_{c2}+k_{d2})/6 \\
&\vdots \\
y_{N} &= y_{N}+(k_{aN}+2k_{bN}+2k_{cN}+k_{dN})/6 \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
となります。

4次ルンゲ=クッタ法のプログラム

実際に例題を解きましょう。
2つの例題を解きます。

[adsense1]

1階微分方程式

1つ目は
\(
\displaystyle \frac{dy}{dx}=-y\sin{x}
\)
です。
一般解は
\(
y=Ae^{\cos{x}}
\)
であり、初期条件\(x=0,y=2\)として解けば解析解は
\(
y=2e^{\cos{x}-1}
\)
です。これを4次ルンゲ=クッタ法を用いて解くには、以下のプログラムで実現できます。

解いて、gnuplotで
plot “fort.10”
で数値計算解(赤点)と解析解(緑線)と共に出力すると、こんなグラフが得られます。

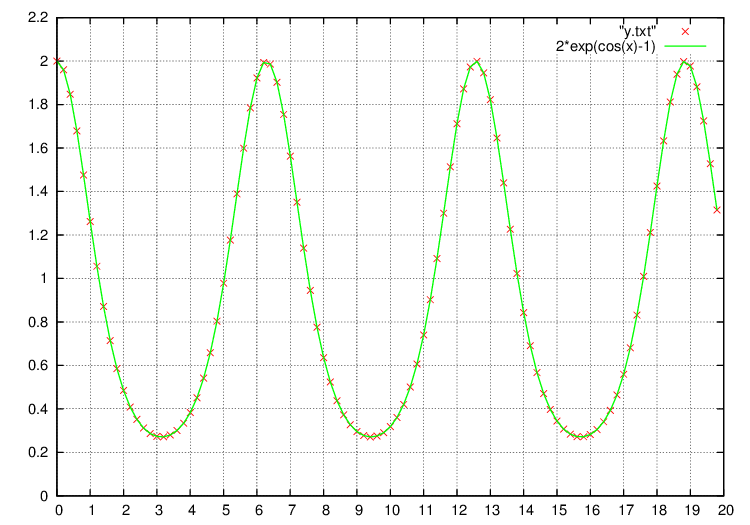
連立1階微分方程式

もう一つの例題は微分方程式
\(
\displaystyle \frac{d^2y}{dx^2}+2\gamma \frac{dy}{dx}+y=0
\)
を解きます。これは物理の世界ではバネの減衰振動を表す運動方程式で(詳しくは減衰振動へ。)、\(0\lt\gamma\lt1\)の場合、解は
\(
y(x)=Ae^{-\gamma x}\cos(x\sqrt{1-\gamma^2}-\alpha)
\)
となります。
\(\gamma=0.15\), 初期条件を今、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\left.y\right|_{x=0} &= 1 \\
\left.\frac{dy}{dx}\right|_{x=0} &= -0.15 \\
\end{aligned}
\right.
\end{eqnarray}
\)
とすると、解析解は
\(
y(x)=e^{-\gamma x}\cos{(x\sqrt{1-0.15^2})}
\)
となります。
プログラムで計算する際は、まず連立1次微分方程式に焼きなおす必要があります。すなわち、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{dy}{dx}&=v \\
\frac{dv}{dx}&=-2\gamma v -y \\
\end{aligned}
\right.
\end{eqnarray}
\)
として解けばいいわけです。

その時の変更するべき場所は少しで、mainとrkfdの一部を変えればおしまいです。
変えた場所をコメントで
!+—+
を入れたので確認してください。

gnuplotで数値計算解(赤点)と解析解(緑線)のグラフを書くとこうでなります。

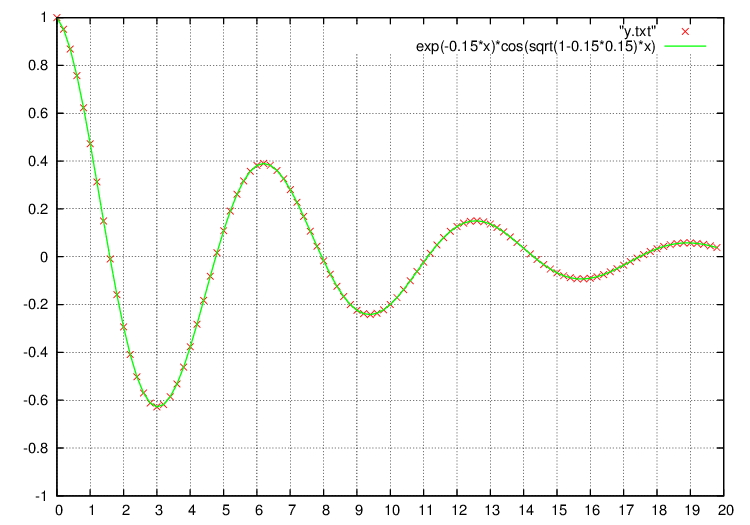
[adsense2]

Tweet