gnuplotで配列はver5.0の時点では実装されていません。
文字を利用することで疑似的な配列が使えます。
まとめ
配列の名前を ” a ” として考えます。
do for [i = 1:5] {
a = a . sprintf('%f ', 0.2*i)
}
plot for [i=1:5] word(a,i)*x
とスクリプトを書き、プロットすると
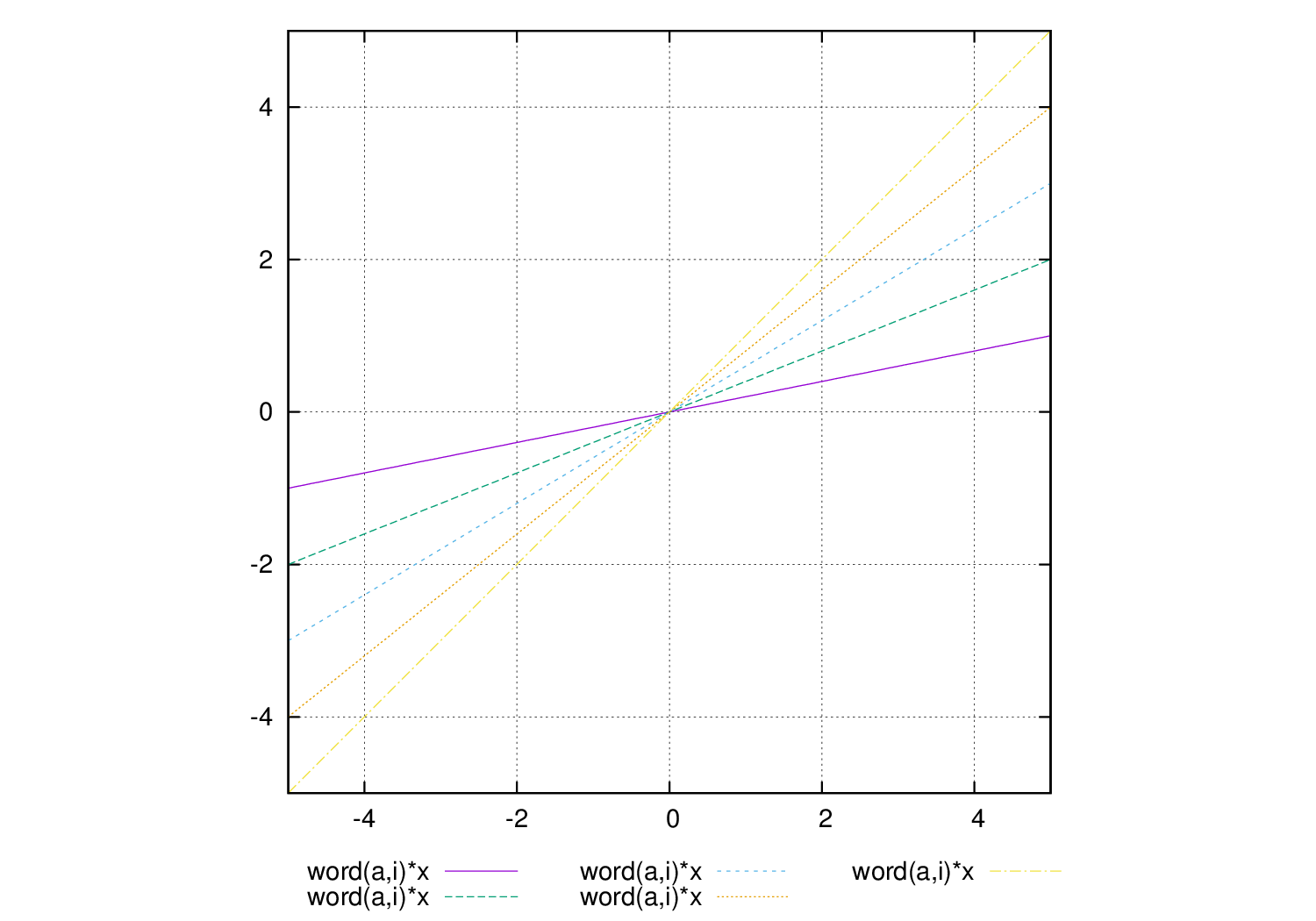
という画像が得られます。
配列の利用
gnuplotでは配列が実装されていません。
doループがver4.6から実装されたことから、これから実装されるかもしれません。
今、
\(
y=0.2x,\;\;0.4x,\;\;0.6x,\;\;0.8x,\;\;x
\)
の合計5つの関数をプロットしたいとします。
もしも素直に考えるならば、スクリプトは
です。これくらいは簡単ですが、複雑になった場合はどうでしょう。そのために疑似配列の使い方を知っておきましょう。
gnuplotで配列は実装されていないので、配列に似たもの(疑似配列と呼ぶことにします)を作ります。
普通のプログラミングでの”配列”のイメージは、番号付けした変数をデータの数だけ用意し、そこに代入していくイメージです。すなわち、
\(a(1)=0.2,\;\; a(2)=0.4,\;\; a(3)=0.6,\;\; a(4)=0.8,\;\; a(5)=1\)
という具合にです。
が、gnuplotでの疑似配列は、空白によって値と値が分けられた1つの文字型変数を用いて作ります。すなわち、
\(a= ” 0.2\;\; 0.4\;\; 0.6\;\; 0.8\;\; 1″ \)
を用意し、呼び出し時に
word(配列名、番号)
というgnuplotに用意されている関数を用いてそれぞれの要素にアクセスします。
この疑似配列aの作り方はこうです。
do for [i = 1:5] {
a = a . sprintf('%f ', 0.2*i)
}
1行目は配列”a”の初期化です。
2~4行目は配列”a”に実際に値を入れていきます。
この形を覚えておけば配列を作ることができます。
配列の呼び出しは、word(,)を用います。1つ目の引数に対象の疑似配列、2つ目の引数に何番目の要素を呼び出すかを指定します。以下のように、
do for [i = 1:5] {
a = a . sprintf('%f ', 0.2*i)
}
plot for [i=1:5] word(a,i)*x
とすればグラフとして書き出されます。
[adsense1]
疑似配列の四則演算
疑似配列の要素に数字を加えたいとします。
その場合は
do for [i=1:5] {
b = b . sprintf('%f ',word(a,i)+1)
}
とすれば疑似配列bに疑似配列aのそれぞれの要素に1加えた値が格納されます。
※同じ配列aにその結果を格納したい場合は最後にa=bを付け加えてください。
疑似配列同士の和を取りたければ、
do for [i=1:5] {
c = c . sprintf('%f ',word(a,i)+word(b,i))
}
とすれば疑似配列\(c(i)\)に(疑似配列\(a(i)\))+(疑似配列\(b(i)\))の値が格納されます。
差ならば-, 積ならば*, 商ならば/に変えてください。
実際に、以下のスクリプトを動かしてみます。
do for [i = 1:5] {
a = a . sprintf('%f ', 0.2*i)
}
print a
b = ''
do for [i=1:5] {
b = b . sprintf('%f ',word(a,i)+1)
}
print b
c = ''
do for [i=1:5] {
c = c . sprintf('%f ',word(a,i)*word(b,i))
}
print c
とすると実行結果
0.200000 0.400000 0.600000 0.800000 1.000000
1.200000 1.400000 1.600000 1.800000 2.000000
0.240000 0.560000 0.960000 1.440000 2.000000
gnuplot>
を得ます。
応用例
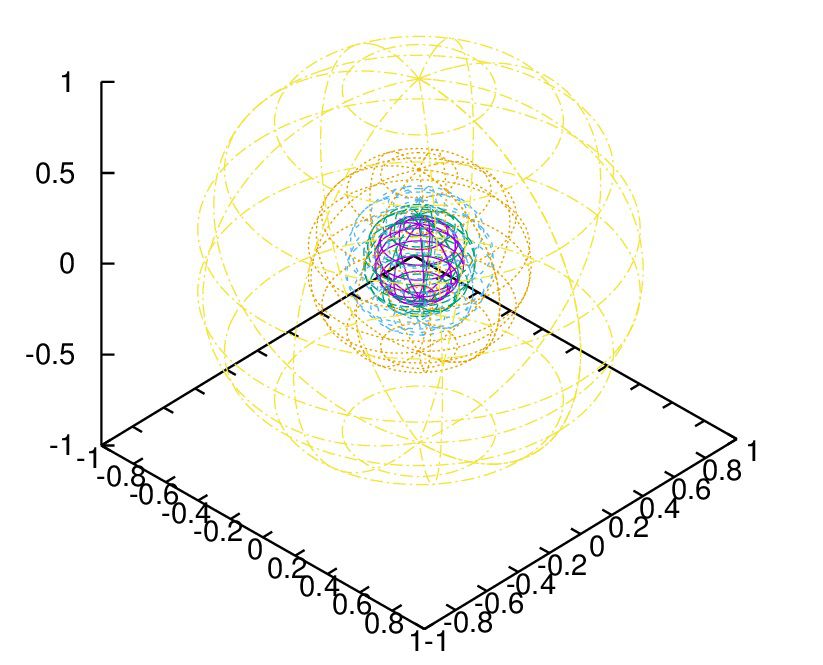
半径の違う複数の球
do for [i = 1:5] {
A = A . sprintf('%f ', 1e0/i)
}
set parametric
set ur[0:pi]
set vr[0:2*pi]
set key below
set ticslevel 0
set view equal xyz
splot for [i=5:1:-1] word(A,i)*sin(u)*cos(v),word(A,i)*sin(u)*sin(v),word(A,i)*cos(u)
アニメーション
A = ''
do for [i = 1:num] {
A = A . sprintf('%f ', 1e0/i)
}
do for [j=1:119] {
t=0.05*j
set view 68,j*1.5,1,1
A=''
do for [i = 1:num] {
A = A . sprintf('%f ', 1e0/sqrt(1+10*sin(t+i*(2e0*pi)/num)**2))
}
splot for [i= num:1:-1 ] word(A,i)*sin(u)*cos(v),word(A,i)*sin(u)*sin(v),word(A,i)*cos(u)
}
を表示に関する設定をして実行すると下のアニメーションが得られます。
参考文献
Operate on 1D arrays in gnuplot
[adsense2][adsense3]