月別アーカイブ: 2019年5月

プログラミングと数値計算

Cubic補間

コメントする

多項式補間です。

Cubic補間 (1次元)

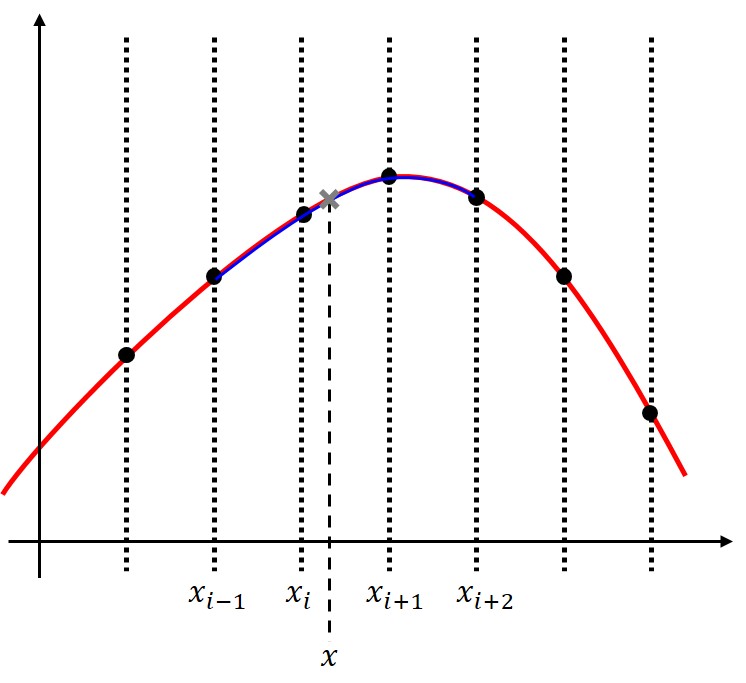
4点を厳密に通る3次多項式によって関数を補間します。
概要は以下の図の通りです。
補間したい点よりも小さいデータ点を2点、大きいデータ点を2点使って補間します。
いわば小さい区間で区切ったラグランジュ補間です。
補間は,既知の係数\(a_{i}\)を用いて関数
\(\displaystyle
g(x)=\sum_{i=0}^{3}a_{i}x^i
\)
誤差は\(O(h^4)\)です。

Fortranプログラムはこちら。

program main
  implicit none
  integer::i,N,M
  double precision::x,f,df,df2,s
  double precision,allocatable::xdata(:),fdata(:)
  double precision::pi=dacos(-1d0)
  double precision,external::cubic
 
  N=30
  M=100
  allocate(xdata(0:N),fdata(0:N))
  xdata=0d0
  fdata=0d0
 
  do i=0,N
     xdata(i)=dble(i)*0.1d0*pi
     fdata(i)=sin(xdata(i))
     write(10,*)xdata(i),fdata(i)
  enddo
 
  ! Cubic-spline interpolation given position as point
  do i=0,M
     x=dble(i)*0.03d0*pi-1d0
     write(11,'(2e20.7e2)')x,cubic(x,N,xdata,fdata)
  enddo
 
  stop
end program main

double precision function cubic(x,N,x0,f0)
  implicit none
  integer,intent(in)::N
  double precision,intent(in)::x,f0(0:N),x0(0:N)
 
  integer::i,i0,i1,i2,i3
  double precision::tx  
  double precision::a,b,c,d,p,q,r,s,t,u

  tx = x-x0(0)
  i1 = 0
  do i=1,N-2
     tx = x-x0(i)
     if(tx.gt.0d0)then
        i1 = i
     else
        exit
     endif
  enddo
  if(i1.eq.0)i1=1
  i0=i1-1
  i2=i1+1
  i3=i1+2

  a = x-x0(i0)
  b = x-x0(i1)
  c = x-x0(i2)
  d = x-x0(i3)  
 
  p = x0(i1)-x0(i0)
  q = x0(i2)-x0(i1)
  r = x0(i3)-x0(i2)

  s = x0(i2)-x0(i0)
  t = x0(i3)-x0(i1)

  u = x0(i3)-x0(i0)

  cubic = a*c*( d*f0(i1)/(p*q) + b*f0(i3)/(u*r) )/t &
        - b*d*( c*f0(i0)/(p*u) + a*f0(i2)/(q*r) )/s
 
  return
end function cubic

Bicubic補間 (2次元)

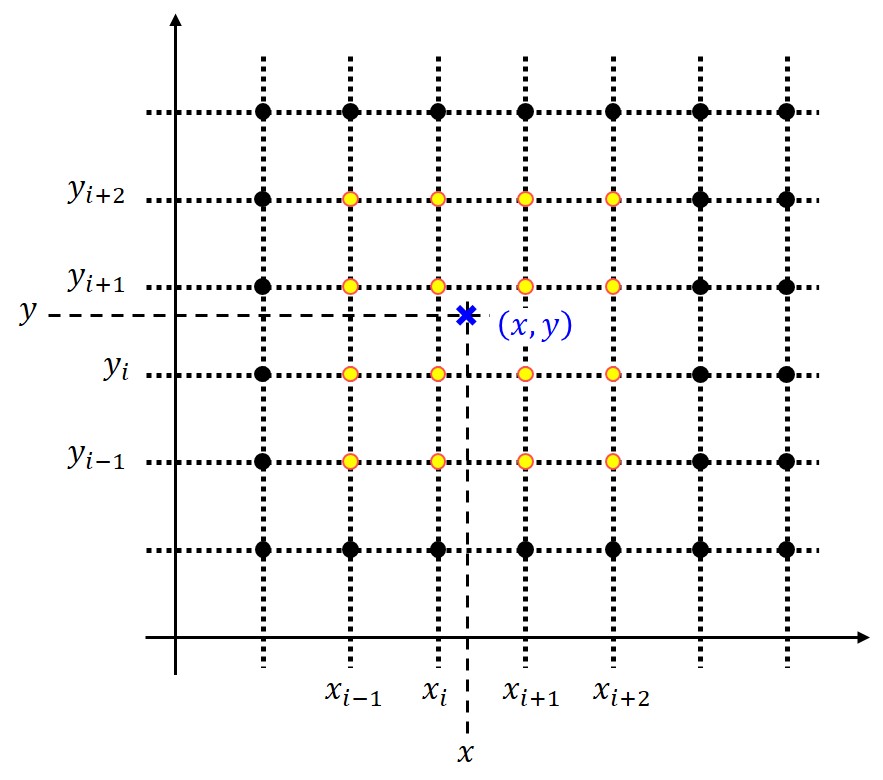
16点を厳密に通る多項式によって関数を補間します。
補間したい点を囲むように存在する16点を用いて補間します。
補間は,既知の係数\(a_{i,j}\)を用いて関数
\(\displaystyle
g(x,y)=\sum_{i=0}^{3}\sum_{j=0}^{3}a_{i,j}x^i y^j
\)
によって行います[1]。誤差は\(O(h^4)\)です。

Fortranプログラムはこちら。

program main
  implicit none
  integer::i,j
  integer::Nx,Ny
  double precision::x,y
  double precision::xa,xb,ya,yb
  double precision,allocatable::x0(:),y0(:),z0(:,:)
  double precision,external::f,ip16

  Nx=20
  Ny=20
  allocate(x0(0:Nx), y0(0:Ny), z0(0:Nx,0:Ny))

  xa=-3d0
  xb= 3d0
  ya=-3d0
  yb= 3d0
   
  ! generate references points
  do i=0,Nx
     x0(i)=dble(i)*(xb-xa)/Nx+xa
  enddo
  do j=0,Ny
     y0(j)=dble(j)*(yb-ya)/Ny+ya
  enddo
  do i=0,Nx
     do j=0,Ny
        z0(i,j)=f(x0(i),y0(j))
        write(10,*)x0(i),y0(j),z0(i,j)
     enddo
     write(10,*)
  enddo
 
  ! Return interpolated results
  do i=0,50
     do j=0,50
        x=i*0.03d0-1d0
        y=j*0.03d0-1d0
        write(11,*)x,y,ip16(x,y,Nx,Ny,x0,y0,z0)
     enddo
     write(11,*)
  enddo

  stop
end program main

function f(x,y)
  implicit none
  double precision::f
  double precision,intent(in)::x,y
 
  f=x*y*exp(-x*x-y*y)
 
  return
end function f

double precision function ip16(x,y,Nx,Ny,x0,y0,z0)
  implicit none
  integer,intent(in)::Nx,Ny
  double precision,intent(in)::x,y,x0(0:Nx),y0(0:Ny),z0(0:Nx,0:Ny)
  !
  ! Bicubic interpolation
  !   x0,y0 are sorted by ascending order,
  !   suppose x0 & y0 are equal interval.
  !   z0(x0,y0)
  !
  integer::i,j
  integer::i0,i1,i2,i3
  integer::j0,j1,j2,j3
  double precision::tx,u,u2,u3
  double precision::ty,v,v2,v3
  double precision::a00,a01,a02,a03,a10,a11,a12,a13
  double precision::a20,a21,a22,a23,a30,a31,a32,a33
  double precision::p(0:3,0:3)
 
  if(Nx.le.3.or.Ny.le.3)then
     write(6,*)" *** Error at ip16"
     stop
  endif
 
  tx = x-x0(0)
  i1 = 0
  do i=1,Nx-2
     tx = x-x0(i)
     if(tx.gt.0d0)then
        i1 = i
     else
        exit
     endif
  enddo
  if(i1.eq.0)i1=1
  i0=i1-1
  i2=i1+1
  i3=i1+2

  ty = y-y0(0)
  j1 = 0
  do j=1,Ny-2
     ty = y-y0(j)
     if(ty.gt.0d0)then
        j1 = j
     else
        exit
     endif
  enddo
  if(j1.eq.0)j1=1
  j0=j1-1
  j2=j1+1
  j3=j1+2

 
  p(0,0) = z0(i0,j0)
  p(0,1) = z0(i0,j1)
  p(0,2) = z0(i0,j2)
  p(0,3) = z0(i0,j3)
  p(1,0) = z0(i1,j0)
  p(1,1) = z0(i1,j1)
  p(1,2) = z0(i1,j2)
  p(1,3) = z0(i1,j3)
  p(2,0) = z0(i2,j0)
  p(2,1) = z0(i2,j1)
  p(2,2) = z0(i2,j2)
  p(2,3) = z0(i2,j3)
  p(3,0) = z0(i3,j0)
  p(3,1) = z0(i3,j1)
  p(3,2) = z0(i3,j2)
  p(3,3) = z0(i3,j3)
   
  a00 = p(1,1)
  a01 = -0.5d0*p(1,0) + 0.5d0*p(1,2)
  a02 = p(1,0) - 2.5d0*p(1,1) + 2*p(1,2) - 0.5d0*p(1,3)
  a03 = -0.50d0*p(1,0) + 1.50d0*p(1,1) - 1.50d0*p(1,2) + 0.5d0*p(1,3)
  a10 = -0.50d0*p(0,1) + 0.50d0*p(2,1)
  a11 =  0.25d0*p(0,0) - 0.25d0*p(0,2) - 0.25d0*p(2,0) + 0.25d0*p(2,2)
  a12 = -0.50d0*p(0,0) + 1.25d0*p(0,1) - p(0,2) + 0.25d0*p(0,3) &
       + 0.50d0*p(2,0) - 1.25d0*p(2,1) + p(2,2) - 0.25d0*p(2,3)
  a13 =  0.25d0*p(0,0) - 0.75d0*p(0,1) + 0.75d0*p(0,2) - 0.25d0*p(0,3) &
       - 0.25d0*p(2,0) + 0.75d0*p(2,1) - 0.75d0*p(2,2) + 0.25d0*p(2,3)
  a20 = p(0,1) - 2.5d0*p(1,1) + 2.d0*p(2,1) - 0.5d0*p(3,1)
  a21 = -0.50d0*p(0,0) + 0.5d0*p(0,2) + 1.25d0*p(1,0) - 1.25d0*p(1,2) &
       - p(2,0) + p(2,2) + 0.25d0*p(3,0) - 0.25d0*p(3,2)
  a22 =  p(0,0) - 2.5d0*p(0,1) + 2.0d0*p(0,2) - 0.50d0*p(0,3) &
       - 2.5d0*p(1,0) + 6.25d0*p(1,1) - 5d0*p(1,2) + 1.25d0*p(1,3) &
       + 2.0d0*p(2,0) -  5.0d0*p(2,1) + 4d0*p(2,2) - p(2,3) &
       - 0.50d0*p(3,0) + 1.25d0*p(3,1) - p(3,2) + 0.25d0*p(3,3)
  a23 = -0.50d0*p(0,0) + 1.50d0*p(0,1) - 1.50d0*p(0,2) + 0.5d0*p(0,3) &
       + 1.25d0*p(1,0) - 3.75d0*p(1,1) + 3.75d0*p(1,2) - 1.25d0*p(1,3) &
       - p(2,0) + 3*p(2,1) - 3*p(2,2) + p(2,3) &
       + 0.25d0*p(3,0) - 0.75d0*p(3,1) + 0.75d0*p(3,2) - 0.25d0*p(3,3)
  a30 = -0.50d0*p(0,1) + 1.50d0*p(1,1) - 1.50d0*p(2,1) + 0.5d0*p(3,1)
  a31 =  0.25d0*p(0,0) - 0.25d0*p(0,2) - 0.75d0*p(1,0) + 0.75d0*p(1,2) &
       + 0.75d0*p(2,0) - 0.75d0*p(2,2) - 0.25d0*p(3,0) + 0.25d0*p(3,2)
  a32 = -0.50d0*p(0,0) + 1.25d0*p(0,1) - p(0,2) + 0.25d0*p(0,3) &
       + 1.50d0*p(1,0) - 3.75d0*p(1,1) + 3*p(1,2) - 0.75d0*p(1,3) &
       - 1.50d0*p(2,0) + 3.75d0*p(2,1) - 3*p(2,2) + 0.75d0*p(2,3) &
       + 0.50d0*p(3,0) - 1.25d0*p(3,1) + p(3,2) - 0.25d0*p(3,3)
  a33 =  0.25d0*p(0,0) - 0.75d0*p(0,1) + 0.75d0*p(0,2) - 0.25d0*p(0,3) &
       - 0.75d0*p(1,0) + 2.25d0*p(1,1) - 2.25d0*p(1,2) + 0.75d0*p(1,3) &
       + 0.75d0*p(2,0) - 2.25d0*p(2,1) + 2.25d0*p(2,2) - 0.75d0*p(2,3) &
       - 0.25d0*p(3,0) + 0.75d0*p(3,1) - 0.75d0*p(3,2) + 0.25d0*p(3,3)
 
  ! Parallel translation u,v [0:1]
  u  = (x-x0(i1))/(x0(i2)-x0(i1))
  v  = (y-y0(j1))/(y0(j2)-y0(j1))
  u2 = u*u
  u3 = u2*u
  v2 = v*v
  v3 = v2*v
  ip16=  (a00 + a01 * v + a02 * v2 + a03 * v3)      &
       + (a10 + a11 * v + a12 * v2 + a13 * v3) * u  &
       + (a20 + a21 * v + a22 * v2 + a23 * v3) * u2 &
       + (a30 + a31 * v + a32 * v2 + a33 * v3) * u3

  return
end function ip16

補間 (2次元)

Bicubic補間の低次元バージョンです。
補間したい点を囲むように存在する4点を用いて補間します。
一応Four point Formulaと名づけられています[2]。
補間は,既知の係数\(a_{i,j}\)を用いて関数
\(\displaystyle
g(x,y)=\sum_{i=0}^{1}\sum_{j=0}^{1}a_{i,j}x^i y^j
\)
によって行います[2]。誤差は\(O(h^2)\)です。

function ip4(x,y,Nx,Ny,x0,y0,z0)
  implicit none
  integer,intent(in)::Nx,Ny
  double precision,intent(in)::x,y,x0(1:Nx),y0(1:Ny),z0(1:Nx,1:Ny)
  double precision::ip4
  !
  ! 2D Interpolation, 4-point formula,
  !           xy equal distance grid
  !
  integer::i,ix0,ix1,iy0,iy1
  double precision::tx,ty,dx,dy,p,q

  tx=1d100
  ix0=1
  do i=2,Nx
     if(abs(x-x0(i)).le.tx)then
        tx=abs(x-x0(i))
        ix0=i
     endif    
  enddo
  tx=1d100
  ix1=1
  do i=2,Nx
     if(i.ne.ix0)then
        if(abs(x-x0(i)).le.tx)then
           tx=abs(x-x0(i))
           ix1=i
        endif
     endif
  enddo

  ty=1d100
  iy0=1
  do i=2,Ny
     if(abs(y-y0(i)).le.ty)then
        ty=abs(y-y0(i))
        iy0=i
     endif    
  enddo
  ty=1d100
  iy1=1
  do i=2,Ny
     if(i.ne.iy0)then
        if(abs(y-y0(i)).le.ty)then
           ty=abs(y-y0(i))
           iy1=i
        endif
     endif
  enddo
 
  dx=x0(ix1)-x0(ix0)
  dy=y0(iy1)-y0(iy0)
  p=(x-x0(ix0))/dx
  q=(y-y0(iy0))/dy
 
  ip4=(1d0-p)*(1d0-q)*z0(ix0,iy0) &
     +p*(1d0-q)*z0(ix1,iy0) &
     +(1d0-p)*q*z0(ix0,iy1) &
     +p*q*z0(ix1,iy1)
   
  return
end function ip4

参考文献

[1]Cubic interpolation
[2]Abramowitz and Stegun.
Handbook of Mathematical Functions.

プログラミングと数値計算

LU分解による連立一次方程式の解法

コメントする

数値計算ライブラリLapackを使って線形連立一次方程式
\(
\begin{equation}
A\mathbf{x}=\mathbf{b}
\end{equation}
\)
をLU分解を用いて数値的に解くプログラムを載せます。

詳しくは説明しませんが、逆行列を用いて解く方法と比べ、
行列が疎である時(行列要素にゼロが多い時)に比較的計算量が減らせます。
また、逆行列を求める際に生じる桁落ちの問題を回避することが出来ます。

解法

連立一次方程式
\(
\begin{equation}
A\mathbf{x}=\mathbf{b}
\end{equation}
\)
を行列\(A\)のLU分解を利用して解きます。
ここで、未知なのはベクトル\(\mathbf{x}\)、既知なのは行列\(A\)とベクトル\(\mathbf{b}\)です。

\(A\)がLU分解されているとします。
すなわち、行列\(A\)に適当な操作を施して、

\(
\begin{align}
A=LU
\end{align}
\)
と書けているとします。ここで、行列\(L, U\)は下三角行列、上三角行列であり、
\(
\begin{align}
L=
\left(
\begin{array}{*4{>{\displaystyle}c}}
1&0&\cdots &0 \\[1em]
l_{2,1}&1&\cdots &0 \\[0.5em]
\vdots&\vdots&\ddots&\vdots \\[0.3em]
l_{s,1}&l_{s,2}&\cdots &1
\end{array}
\right) ,~~~
U=
\left(
\begin{array}{*4{>{\displaystyle}c}}
u_{1,1}&u_{1,2}&\cdots &u_{1,s} \\[1em]
0&u_{2,2}&\cdots &u_{2,s} \\[0.5em]
\vdots&\vdots&\ddots&\vdots \\[0.3em]
0 & 0 &\cdots &u_{s,s}
\end{array}
\right)
\end{align}
\)

という行列です。
もし、行列\(A\)がLU分解されていれば、

\(
\begin{align}
& A\mathbf{x}=\mathbf{b} \\
& LU\mathbf{x} = \mathbf{b} \\
& L\mathbf{w} = \mathbf{b}~~~…(*)
\end{align}
\)

と書けます。ここで、\(\mathbf{w} \equiv U\mathbf{x}\)と置きました。
まず、式(*)を解いて、\(\mathbf{w}\)を求めます。これは、下三角行列に対する問題なので、前進代入を用いて簡単に解くことが出来ます。

続いて、
\(
U\mathbf{x}=\mathbf{w}
\)
を後退代入を利用して解\(\mathbf{x}\)を求めます。

以上がLU分解を利用して連立一次方程式を解く方法です。
数値計算のルーチンは大きく2つのステップに分かれており、

  1. 行列\(A\)のLU分解を求める(ルーチン dgetrf)
  2. LU分解された行列\(A\)を用いて連立一次方程式を解く(ルーチン dgetrs)

というステップです。
これは、例えば問題
\(
\begin{equation}
A\mathbf{x}=\mathbf{b}
\end{equation}
\)
と
\(
\begin{equation}
A\mathbf{x}=\mathbf{b’}
\end{equation}
\)
の右辺だけが変わる複数の問題を解きたい場合なんかに便利です。この問題の場合、行列\(A\)は変わらないため、LU分解した結果を両方の問題に流用することが出来るのです。

プログラム

プログラムは以下の通りです。
いつもと同じように、ワーク配列を減らす為だけに導入したルーチンを挟んでいます。

program main
  implicit none
  integer::i,N
  double precision,allocatable::a(:,:),b(:),x(:)
  integer,allocatable::ipiv(:)
 
  N=3
  allocate(a(1:N,1:N))
  allocate(ipiv(1:N),b(1:N),x(1:N))
  a(1,1:N)=(/1d0,3d0,5d0/)
  a(2,1:N)=(/0d0,3d0,1d0/)
  a(3,1:N)=(/6d0,2d0,5d0/)
  b(1:N)=(/33d0,10d0,66d0/)

  do i=1,N
     write(6,'(3f10.5)')a(i,1:N)
  enddo

  call LUfact(N,a,ipiv)
  call axbsolve(N,a,ipiv,b,x)

  write(6,*)"---- solution ----"
  do i=1,N
     write(6,'(2f10.5)')x(i)
  enddo
 
  stop
end program main

subroutine LUfact(N,LU,ipiv)
  implicit none
  integer,intent(in)::N
  double precision,intent(inout)::LU(1:N,1:N)
  integer,intent(out)::ipiv(1:N)  

  ! LU factorization for lapack
  ! Overwrite matrix LU by factorized LU matrix
 
  integer::m,lda,info

  m=N
  lda=N
  call dgetrf(m,N,LU,lda,ipiv,info)
  if(info.ne.0)then
     write(6,*)"**error at LUlapack"
     stop
  endif
 
  return
end subroutine LUfact

subroutine axbsolve(N,LU,ipiv,b,x)
  implicit none
  integer,intent(in)::N
  integer,intent(in)::ipiv(1:N)
  double precision,intent(in)::LU(1:N,1:N),b(1:N)
  double precision,intent(out)::x(1:N)
  !
  ! Solve simultaneous equations by Lapack
  !
  double precision,allocatable::bl(:,:)
  integer::nrhs,lda,ldb,info
  character(1)::trans  
 
  nrhs=1
  trans='N'
  allocate(bl(1:N,1:nrhs))  
  bl(1:N,1)=b(1:N)
  lda=N
  ldb=N
  call dgetrs(trans,N,nrhs,LU,lda,ipiv,bl,ldb,info)
  if(info.ne.0)then
     write(6,*)"**error at LUlapack"
     stop
  endif
 
  x(1:N)=bl(1:N,1)  

  return
end subroutine axbsolve

上のプログラムをlapackと一緒にコンパイルして動かすと、端末上で

> ./a.out
   1.00000   3.00000   5.00000
   0.00000   3.00000   1.00000
   6.00000   2.00000   5.00000
 -------------
   7.00000
   2.00000
   4.00000
>

という結果が得られるかと思います。
これは、連立一次方程式
\(
\begin{align}
\left(
\begin{array}{ccc}
1& 3& 5 \\
0& 3& 1 \\
6& 2& 5
\end{array}
\right)
\left(
\begin{array}{ccc}
x \\
y \\
z
\end{array}
\right)
=
\left(
\begin{array}{ccc}
33 \\
10 \\
66
\end{array}
\right)
\end{align}
\)
を解いた結果です。
解析解(\(x=7, y=2, z=4\))は、例えばwolframを利用して求められます。
{{1,3,5},{0,3,1},{6,2,5}}.{x,y,z}=={33,10,66} –wolfram alpha