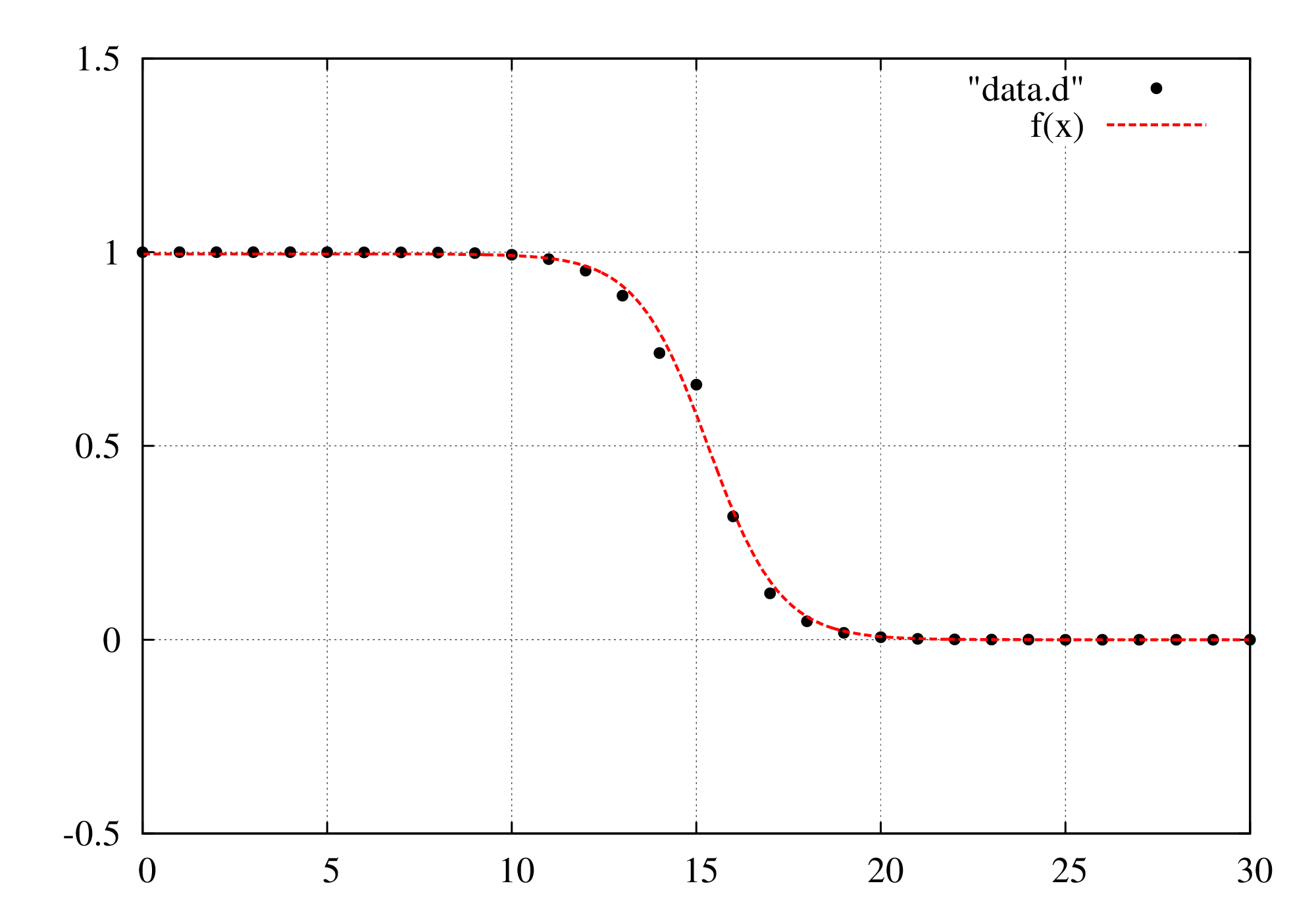
ここでは、非線形方程式の解を数値的に求める方法である、
二分法、
挟み撃ち(False position)法、
Anderson-Björk法、
Brent法、
Newton法、
Steffensen法
等について紹介します。

1. 問題設定
2. まとめ
3. 数値解法
• 二分法
• 挟み撃ち(False position)法
• Anderson-Björk法
• Brent法
• Newton法
• Steffensen法
4. 複数のゼロ点を見つけたい場合

問題設定

区間\([a,b]\)で定義された実関数\(f(x)\)に
\(
f(x)=0
\)
を満たす\(x\)が1つある。\(x\)を求めよ。但し\(f(a),f(b)\ne 0\)。

まとめ

1変数の場合：Brent法(二分法と逆2次補間、挟み撃ち法の組み合わせ)
多変数の場合：Newton法
を使うのが良いでしょう。

数値解法

１変数の問題で、
教育上良く使われる方法は二分法
実用的な手法はBrent法
です。
またNewton法は多変数の場合にも複素数の場合でも容易に拡張できるので、その意味で実用的です。

区間\([a,b]\)にゼロ点が１つ存在する事を数学的に言えば、\(f(a)f(b)\lt 0\)ということです。

二分法

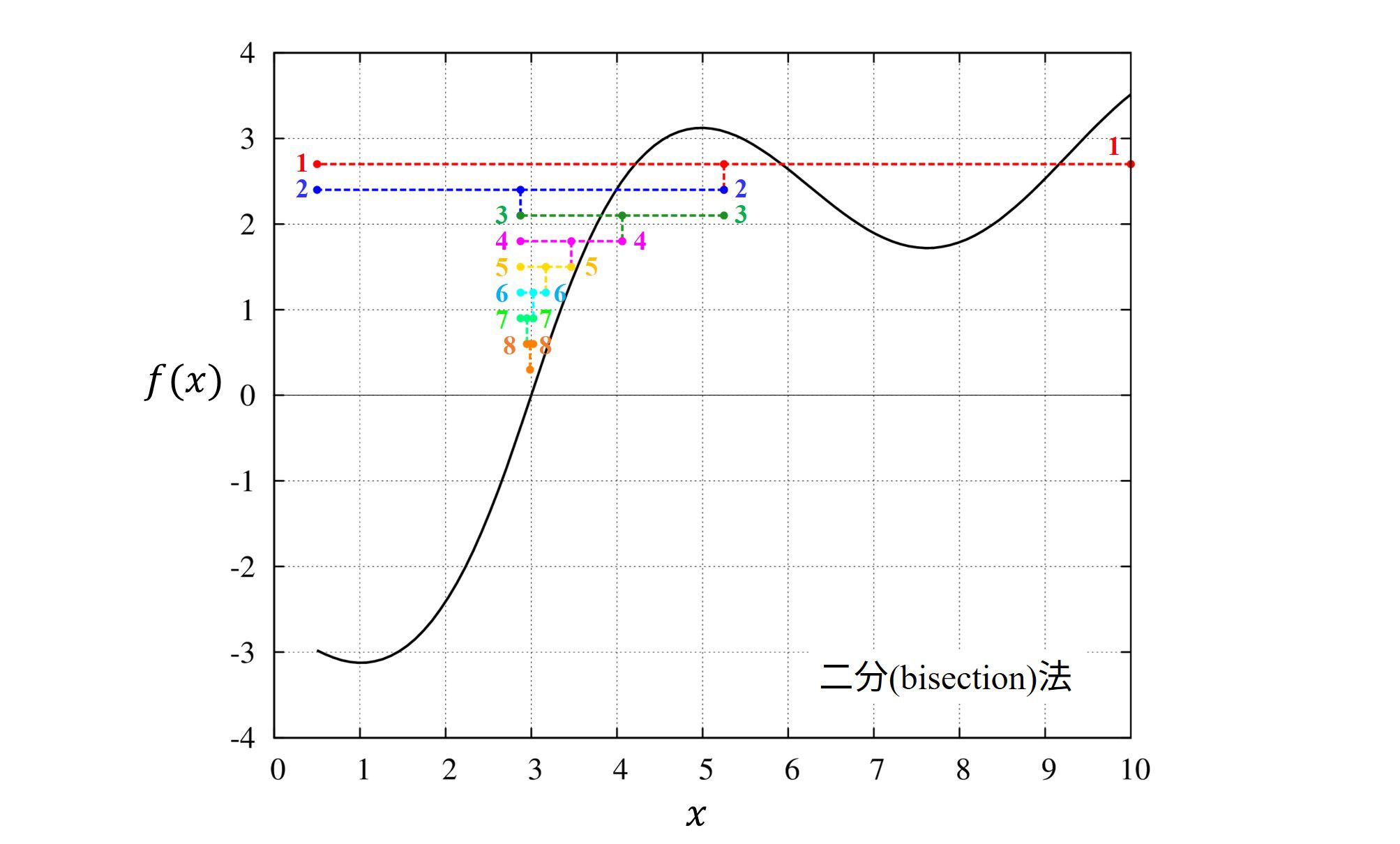
要点

・解が確実に見つかります。
・関数の振る舞いが非連続であっても、たちが悪い関数でも確実ですが、収束は遅いです。

計算方法

二分法は位置\([a,b]\)における関数の符号の情報だけを見てゼロ点を推測します。
なので、区間内にゼロ点がある事が分かっていれば、そこを境として符号が違うので確実に解を囲い込んでいくことが出来ます。
教育的に分かりやすい方法であり、根を探すにあたり失敗が無い方法ですが、
滑らかな関数であっても計算時間がかかるため、あまり実用的ではありません。

収束速度について

2分法では、1回の計算あたり範囲が\(1/2\)になるため、漸化式
\(
\displaystyle \varepsilon_n=\varepsilon_{n-1}\cdot 2^{-1}
\)
が成立するため、
\(
\varepsilon_n=\varepsilon_{0}\cdot 2^{-n}
\)
が導けます。ここで\(\varepsilon_{0}\)は初期のxの範囲(\(\varepsilon_0=|b-a|\))を表します。
収束精度と計算回数の関係を決めるためにはnについて解いて、
\(
\begin{align}
\varepsilon_n &=2^{-n} \varepsilon_{0} \\
2^n &=\frac{\varepsilon_0}{\varepsilon_n} \\
n &=\log_2\left(\frac{\varepsilon_0}{\varepsilon_n}\right) \\
\mbox{または}& \\
n &=\frac{\ln\left(\varepsilon_0/\varepsilon_n\right)}{\ln{2}}
\end{align}
\)
より、例えば初期の解の範囲(\(\varepsilon_0\))を1, 解を\(10^{-14}\)まで収束させようとすれば、大体\(n=47\)となり、47回、2分法を繰り返す必要があります。
逆に言えば、どんな状況でも47回繰り返せば相対誤差を14桁収束させることが出来るということです。

収束の判定は
要求精度\(\epsilon_{\text{tol}}\)、機械精度\(\epsilon_{\text{mac}}\)、解の存在範囲\(\delta\)、新たな解の推定値\(x\)、
とすると、
\(
\delta \lt 4\epsilon_{\text{mac}}|x|+\epsilon_{\text{tol}}
\)
もしくは
\(
f(x)=0
\)
で判定します。
この意味は、解の存在範囲を\(\pm 2\epsilon_{\text{mac}}\)の範囲まで特定するか、解の存在範囲が要求精度\(\epsilon_{\text{tol}}\)まで達するかのどちらかが満たされるかで判定します。

Fortranプログラムはこちら。

二分法でやると以下の通り20回必要になります。

6桁収束するために24回も評価回数が必要です。
計算時間を気にしないのならば良い方法ですが、やはり遅いです。

挟み撃ち法(False position法)

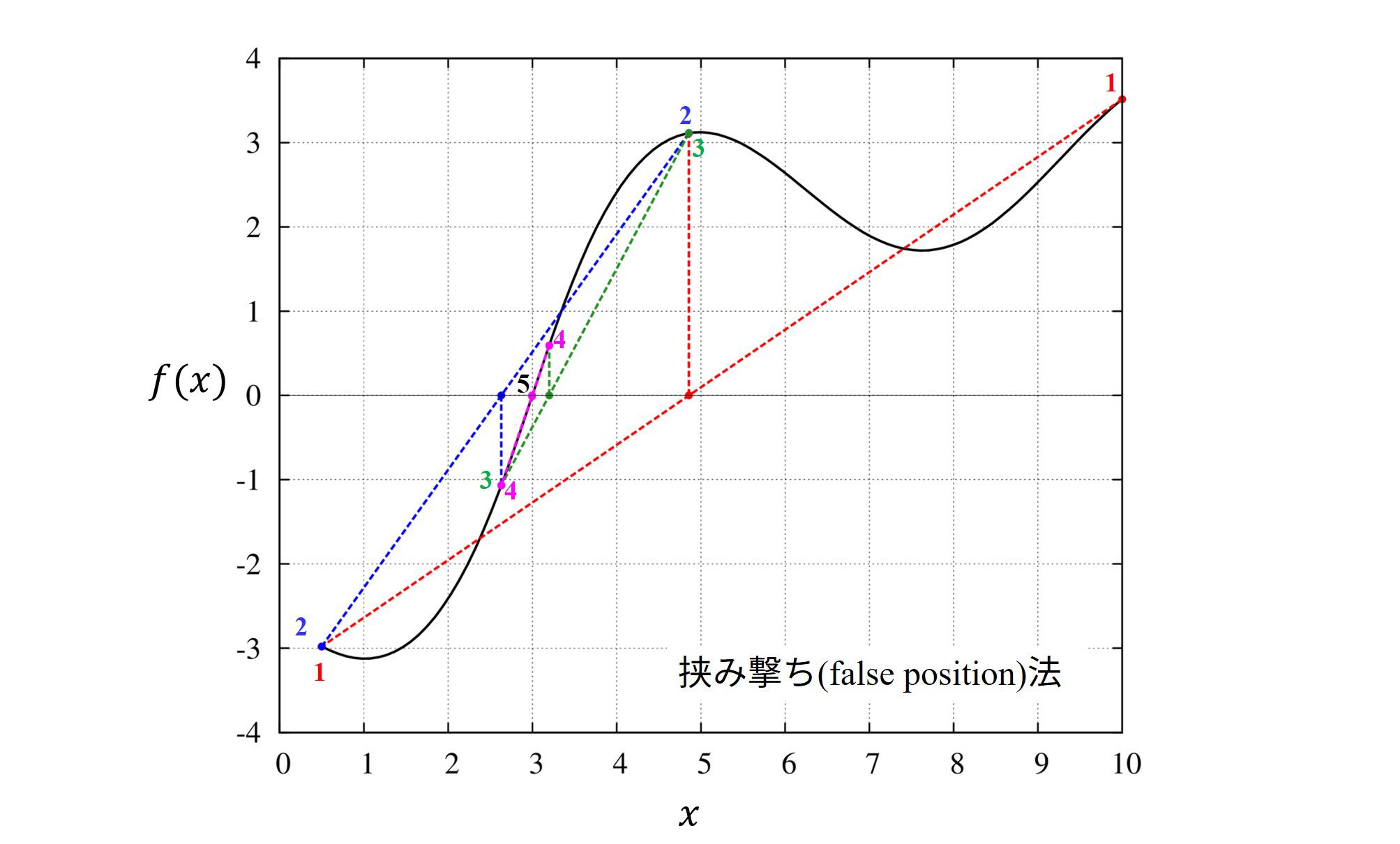
要点

・解が確実に見つかります。
・勢いよくゼロ点を横切っていない場合、収束が遅くなります。

計算方法

二分法との違いはゼロ点の推測に用いる情報量です。
二分法では位置\([a,b]\)における関数の符号だけを見てゼロ点を推測しますが、
挟み撃ち法では位置\([a,b]\)における関数の値も見てゼロ点を推測しています。
この挟み撃ち法の推測は、点\((a,f(a)),(b,f(b))\)を結ぶ直線が通るゼロ点して値を推測するのです。

一つ、挟み撃ち法の説明を見ていた時に、解の囲い込み方法が2通りあるようです。
オリジナルのものは片方の点を絶対に変えない方法のようですが、二分法と同じように決めている物もあります。

ここでは、二分法と同じように決めていく後者の方法を載せておきます。
二分法の新しい点を決める所だけ変えればプログラムは完了です。

要求精度を6桁にすると、実行結果は

となり、初めの1回は無視すると6回で収束に至っていることが分かります。早いですね。

Anderson-Björk法

アンダーソン・ビョーク法と呼ばれるアルゴリズムです。
詳しくは
求根アルゴリズム 挟み撃ち法 / イリノイ法 / アンダーソン・ビョーク法 [2/3] -サブロウ丸
のページが詳しいのでそちらを参照してください。

この方法は割線法が遅くなってしまう時の対処です。

Brent法

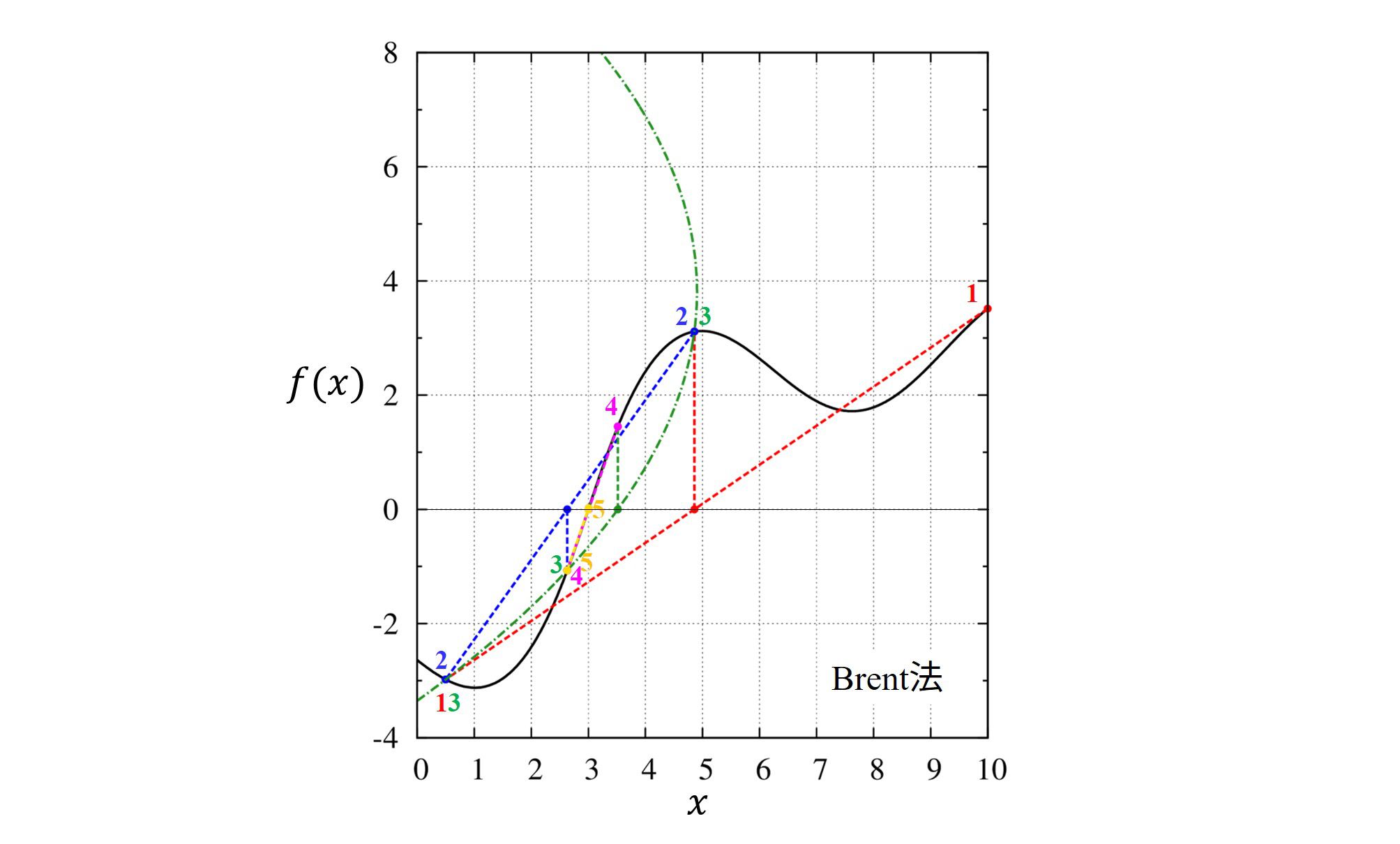
要点

・解が確実に見つかります。
・基本的には逆二次補間(inverse quadratic interpolation)で根を探索します。
・逆二次補間が原理的に出来ない場合（二つ以上の関数値が同じ場合など）では挟み撃ち法を行います。
・”探索が失敗”した時は二分法に切り替えて根を探します。
・1変数の場合、実用的な方法として推奨されています。

計算方法

逆二次補間は3点を結ぶ逆二次関数(上下に凸ではなく、左右に凸をもつ関数)としてラグランジュ補間をして、その根をゼロ点の位置として用いる方法です。
しかし、逆二次補間を行う際に必要な3点の内、2点以上が同じ関数値を持つと解が発散する、という問題があるため、その時は挟み撃ち法に切り替えて計算を行います。

二分法は、逆二次補間や挟み撃ち法を用いた為に解の収束が遅くなる、と判定されたときに使われます。

実際に動かしてみると逆二次補間よりも挟み撃ち法が使われる頻度が多いようです。

詳細は(Van Wijngaarden-Dekker-Brent法, William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery著, 丹慶勝市ら訳（1993) 『Numerical Recipes in C [日本語版]C言語による数値計算のレシピ』 技術評論社 261pp.)に書いてありますので、こちらを参照してください。

プログラム自体はパブリックドメインのNetlibにあるもの(zeroin.f)を基本としましょう。ただし、Fortran77で掛かれているので並列計算を考えた時に厄介です。文番号を消したものを置いておきます。

要求精度を6桁にすると、実行結果は

となり、初めの1回は無視すると7回で収束に至っていることが分かります。挟み撃ち法とだいたい同じです。

Netlibがpublicdomainであることの記述は以下の本にも見ることが出来ます。
https://books.google.de/books?id=2GPNBQAAQBAJ&pg=PA109&lpg=PA109&dq=netlib+public+domain&source=bl&ots=d6Uw8D5JMv&sig=Dw3wXTAQThFKLVrL7pm_qnCaq9s&hl=de&sa=X&ved=0ahUKEwjO05Xxt_XKAhXCwxQKHUBlC5sQ6AEIXjAI#v=onepage&q=netlib%20public%20domain&f=false

ちなみにですが、wikipediaにあるBrent法の疑似コードを実装したのですが、うまく働きませんでした。
Brent’s method　-wikipedia en
ブレント法　-wikipedia ja

Newton法

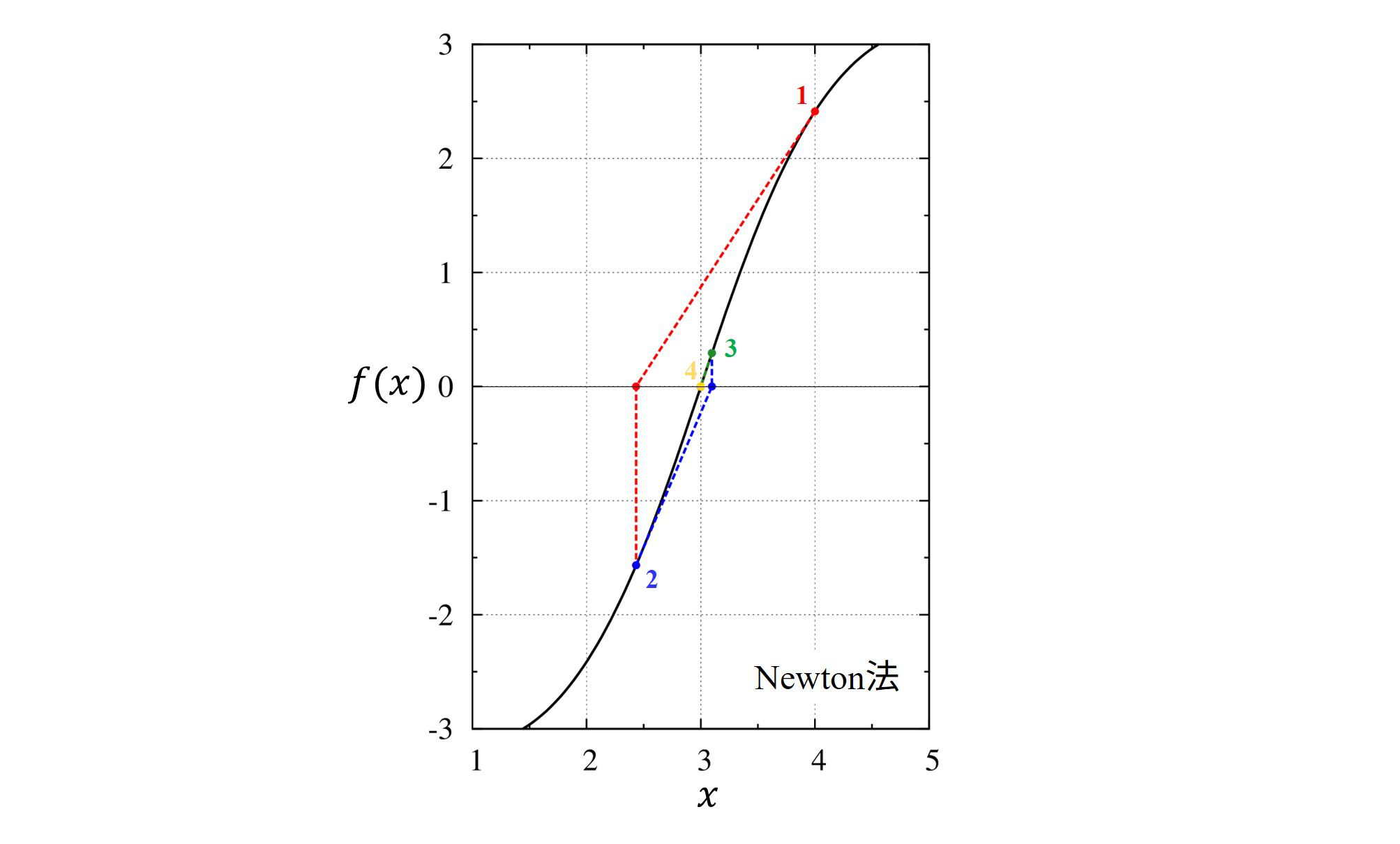
要点

・解近傍のただ1点から収束させるので必要な情報が少なく済みます。
・解近傍のただ1点上における関数の微分を用いて収束させ、一回の計算で一致桁数が倍になります。
・本当に解の近くから始めないと、失敗します。
・多変数への拡張が容易ですが、関数の微分を数値微分で代用すると効率が落ちます。

計算方法

ニュートン法について詳しくは
ニュートン法（1、2次元、多次元）
に書いたので、こちらを参照してください。

プログラムは以下のもので、

実際に実行すると

という結果を得ます。

番外編：Steffensen法(Steffensen’s method)

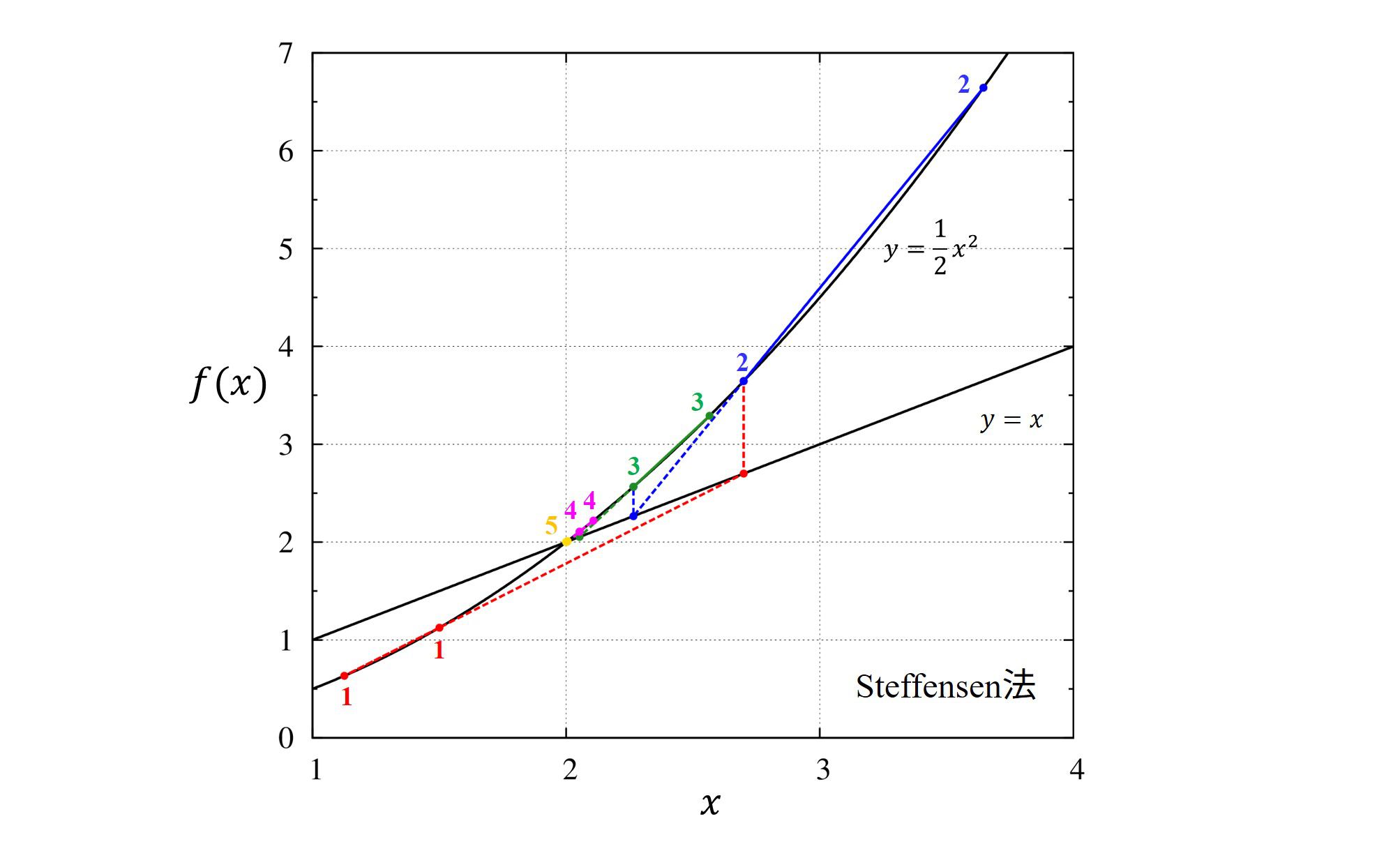
Steffensen法は自己無撞着方程式を解くために使われる方法で、Newton法に似ています。
特に良く使われるのは、方程式がたまたま
\(
x=g(x)
\)
と書けている特定の方程式を満たす\(x\)を探す場合に使われます。

ですが、
\(
f(x)=x-g(x)
\)
を考えれば
\(
f(x)=0
\)
を考える問題と同じ、ということになります。
ここでは、方程式
\(
x=x^2/2
\)
を満たす\(x\)を探す問題を考えます。

この問題は
\(
x-x^2/2=0
\)
と同じです。

計算手法は
htt://park.itc.u-tokyo.ac.jp/kato-yusuke-lab/nagai/note_070420_self.pdf
でまとめられている通り、

\(
\begin{align}
a&=g(x_n), \\
b&=g(a),\\
x_{n+1}&=x_n-\frac{(a-x_n)^2}{b-2a+x_n}
\end{align}
\)
の漸化式で求められます。

プログラムではこちら。

複数のゼロ点を見つけたい場合

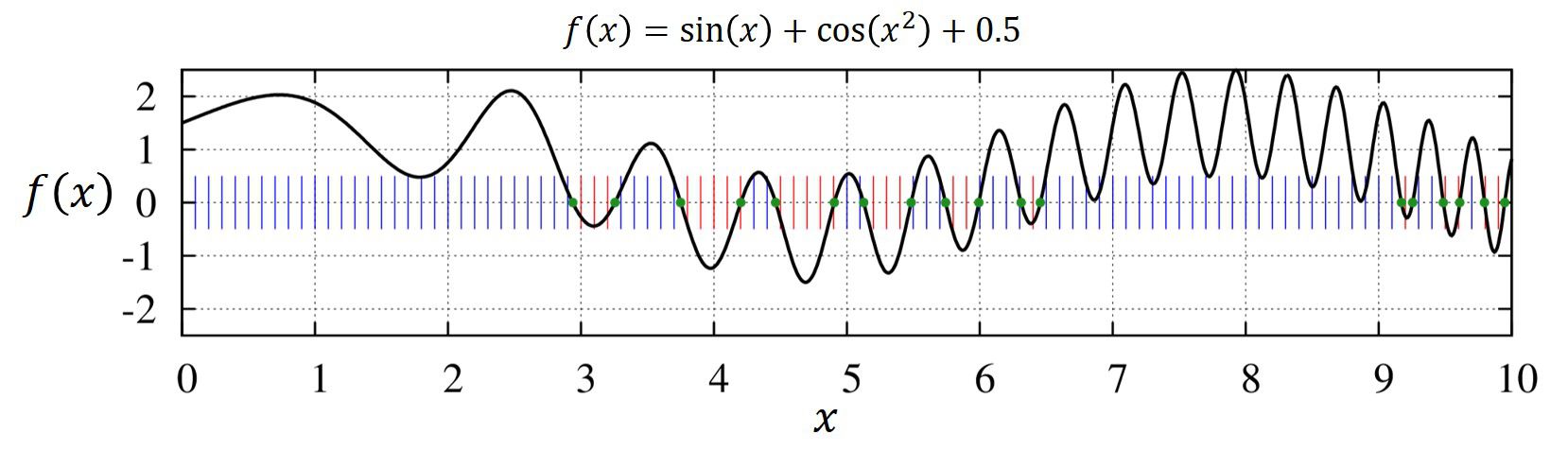
複数のゼロ点を見つけたい場合、一つの方法として、

解のある区間の特定→収束

を繰り返すことで得られる、と考えられるでしょう。

具体的には計算区間を荒く区切り、符号が変わる範囲を特定、その符号が変わる範囲に対してのみゼロ点を探すのです。

上の図の縦線は等間隔に荒く探した時の、関数が正になる時に青、負の時に赤色に表示しています。
収束した結果が緑の点です。

fortranプログラムはこんな感じになります。

導関数を用いたゼロ点の探索

関数のゼロ点の間隔が非常に短い時に便利です。
等間隔に区切ってから探すという考えは同じです。
まず、導関数のゼロ点を探します。
ゼロ点が存在するならば関数のゼロ点は導関数のゼロ点に挟まれたところにあるので、その情報を元に探します。
導関数を解析的に与えていますが、もしも高精度にゼロ点を決めたい場合、二重数を用いた導関数の取得が良いかもしれません。

プログラムは例えば以下の通りです。