sikino のすべての投稿

プログラミングと数値計算

fortranコンパイラのコマンド

コメントする

ここではgfortranとifortでのコンパイル時に指定できるコマンド(最適化とデバッグ、mklの使用とopenmp)について記述します。

ここで対象とするファイル名をmain.f90にします。

最適化

  • gfortran
    gfortran -O3 -fopenmp main.f90
  • ifort
    ifort -mkl -openmp -xHOST -ipo -O3 main.f90

としてコンパイルするといいかと。並列計算がいらない場合は-fopenmp, -openmpのオプションを消してください。

デバッグ

デバッグとはバグを取り除いて望み通りのものにする作業です。

  • gfortran
    gfortran -Wall -fbounds-check -O -Wuninitialized -ffpe-trap=invalid,zero,overflow -fbacktrace -g main.f90
  • ifort
    ifort -mkl -check all -warn all -gen_interfaces -fpe0 -ftrapuv -traceback -g main.f90

とするのがいいでしょう。

※gfortranでは、オプション -ffpe-trap=invalid,zero,overflowが悪さすることがあるようです。fortranでのエラーメモにも書いたように、エラーを起こすはずがないコードでもなぜかエラーと言われることがあります。その時は

gfortran -Wall -fbounds-check -O -Wuninitialized -fbacktrace -g main.f90

でデバッグをやると良いでしょう。

[adsense1]

gfortranでMKLを使う

例えばgfortranコンパイラでIntel® Math Kernel Library (Intel® MKL) を並列計算も含めて使いたいとします。

今、こういう状況にあるとします。

・MKLがあり、/opt/intel/の中にあるディレクトリ”mkl”
が存在する状況下で
・gfortranコンパイラ
がある。

とします。MKLのバージョンによってコンパイルオプションが異なるので注意してください。
Intel® Math Kernel Library Link Line Advisorを見ればどういうコマンドを打てばいいのかを教えてくれます。

ここではMKLのバージョンが
Ver. 11.1
と
Ver. 10.2.5.035
の場合の具体例を載せます。

MKLver11.1の場合
gfortran -fdefault-integer-8 -fopenmp -m64 -I/opt/intel/mkl/include -Wl,--start-group /opt/intel/mkl/lib/intel64/libmkl_gf_ilp64.a /opt/intel/mkl/lib/intel64/libmkl_core.a /opt/intel/mkl/lib/intel64/libmkl_gnu_thread.a -Wl,--end-group -ldl -lpthread -lm main.f90
MKLver10.2.5.035の場合
gfortran -fopenmp -m64 -I/opt/intel/mkl/include /opt/intel/mkl/lib/em64t/libmkl_solver_lp64.a -Wl,--start-group /opt/intel/mkl/lib/em64t/libmkl_gf_lp64.a /opt/intel/mkl/lib/em64t/libmkl_core.a /opt/intel/mkl/lib/em64t/libmkl_gnu_thread.a -Wl,--end-group -lpthread -lm main.f90

※もしかしたら/opt/intel/mkl/ではなくて、/opt/intel/mkl/10.2.5.035/じゃないとだめかもしれません。

バージョンが違ったらどうするかはIntel® Math Kernel Library Link Line Advisorを参考にしてください。上のものを得るには下のようにすれば大丈夫です。

 Select Intel® product: (MKLのバージョンは？)  Intel(R) MKL10.2
 Select OS: (OSは何？)  Linux*
 Select usage model of Intel® Xeon Phi™ Coprocessor: 
(走らせようとしているコンピュータのcpuの種類がXeon Phi っていうcpuが数百個あるような特別なもの？)		  –
 Select compiler: (何のコンパイラでMKLを使いたいの？, gfortranだったらGNU fortran.)  GNU Fortran
 Select architecture:(良く分かりません！Help me →I don’t use any flag と進んで、”getconf LONG_BIT” と端末で打って何て表示されたかで入力しました。多分cpuが何ビットか、かな？)  Intel(R) 64
 Select dynamic or static linking:

(動的リンク(dynamic)がいい？静的リンク(static)がいい？
　　　　動的→汎用性あり、容量は軽い、動作は遅い
　　　　静的→汎用性なし、容量は重い、動作は早い )		  Static
 Select interface layer:(プログラムの中に整数型で2^31越えてるものはある？ない？越えてなかったら32bit integer, 越えてたら64bit integer)  LP64 (32-bit integer)
 Select sequential or multi-threaded layer:
(mklのサブルーチンを1つのCPUだけ(sequential)で走らせたい？それとも並列(multi-threaded)にする？)		  multi-threaded
 Select OpenMP library:(openMPの種類は何使う？intel か GNUか→僕は両方試したら、intelでは動かず、GNUでは動きました。)  GNU (libgomp)
 Select cluster library:　ここから下は何を言っているのか分かりませんでした。空白でもいけたから多分直接は関係ないオプションなのだろうと。  

次に下の方で作られたオプションをgfortranコンパイル時にくっつける。
$(MKLROOT)/libem64t/libmkl_solver_lp64.a -Wl,–start-group $(MKLROOT)/libem64t/libmkl_gf_lp64.a $(MKLROOT)/libem64t/libmkl_core.a $(MKLROOT)/libem64t/libmkl_gnu_thread.a -Wl,–end-group -lpthread -lm
と
-fopenmp -m64 -I$(MKLROOT)/include
が作られるかと思います。この２つをくっつければokです。
$(MKLROOT)はディレクトリ”mkl”へのパスです。シェルスクリプトの場合、()は要りません。

ここで、この通りコンパイルしようとすると/libem64t/というディレクトリはないよ、っていわれて出来ませんでした。
実際にたどってみると/lib/em64t/ならあって、これに変えたらコンパイルが成功しました。ケースバイケースかな。

参考

Fortranデバッグ用オプション

[adsense2]

プログラミングと数値計算, 物理学

二重振り子

コメントする

座標の取り方は下図のように取ります。棒の伸び縮みは無いものとします。
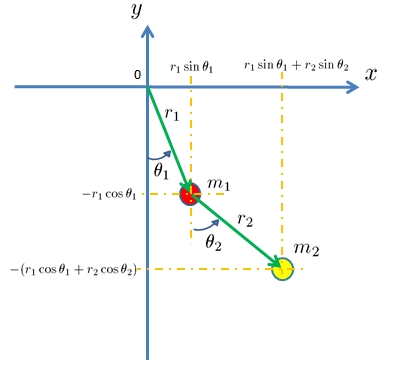
二重振り子座標
どういう解き方でもいいですが、ここでは

  1. デカルト座標\(L(x,y)\)でラグランジアンを記述
  2. デカルト座標から座標変換し、\((r,\theta)\)でラグランジアンを記述
  3. 新たな座標系で運動方程式を導く

という順で解いていきます。

[adsense1]

1, デカルト座標でのラグランジアンLは(運動エネルギーK)-(位置エネルギーU)と書けるため、
\(
L(x_1,\dot{x}_1,y_1,\dot{y}_1,x_2,\dot{x}_2,y_2,\dot{y}_2)\\
\displaystyle =\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2)+\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_2^2)-(-m_1gy_1-m_2gy_2)
\)
と書けます。

2, デカルト座標から座標変換
式を簡単にするために座標変換を行います。新しい座標\((r_1,\theta_1,r_2,\theta_2)\)とデカルト座標\((x_1,y_1,x_2,y_2)\)の関係式は
\(
\begin{align}
x_1&=r_1\sin{\theta_1}\\
y_1&=-r_1\cos{\theta_1}\\
x_2&=r_1\sin{\theta_1}+r_2\sin{\theta_2}\\
y_2&=-r_1\cos{\theta_1}-r_2\cos{\theta_2}
\end{align}
\)
という関係があります。各々を時間で微分すれば、
\(
\begin{align}
\dot{x}_1&=\dot{r}_1\sin{\theta_1}+r_1\dot{\theta}_1\cos{\theta_1}\\
\dot{y}_1&=-\dot{r}_1\cos{\theta_1}+r_1\dot{\theta}_1\sin{\theta_1}\\
\dot{x}_2&=\dot{r}_1\sin{\theta_1}+r_1\dot{\theta}_1\cos{\theta_1}+\dot{r}_2\sin{\theta_2}+r_2\dot{\theta}_2\cos{\theta_2}\\
\dot{y}_2&=-\dot{r}_1\cos{\theta_1}+r_1\dot{\theta}_1\sin{\theta_1}-\dot{r}_2\cos{\theta_2}+r_2\dot{\theta}_2\sin{\theta_2}
\end{align}
\)
これらをラグランジアン\(L(x_1,\dot{x}_1,y_1,\dot{y}_1,x_2,\dot{x}_2,y_2,\dot{y}_2)\)に代入します。すると、新たな座標系でのラグランジアン\(L(r_1,\dot{r}_1,\theta_1,\dot{\theta}_1,r_2,\dot{r}_2,\theta_2,\dot{\theta}_2)\)が得られます。
\(
\begin{align}
L(r_1,\dot{r}_1,\theta_1,\dot{\theta}_1,& r_2,\dot{r}_2,\theta_2,\dot{\theta}_2) \\
=&\frac{1}{2}m_1(\dot{r}_1^2+r_1^2\dot{\theta}_1^2)+\frac{1}{2}m_2\left[\dot{r}_1^2+\dot{r}_2^2+r_1^2\dot{\theta}_1^2+r_2^2\dot{\theta}_2^2 \right. \\
&\left.+2(\dot{r}_1 r_2 \dot{\theta}_2-r_1\dot{r}_2 \dot{\theta}_1)\sin{(\theta_1-\theta_2)}+2(\dot{r}_1 \dot{r}_2 +r_1 r_2 \dot{\theta}_1 \dot{\theta}_2)+\cos{(\theta_1-\theta_2)}\right] \\
&+m_1gr_1\cos{\theta_1}+m_2g(r_1\cos{\theta_1}+r_2\cos{\theta_2})
\end{align}
\)

僕は先ほど式を簡単にするために座標変換をする、といいました。しかし、新しい座標系におけるラグランジアンはどう見ても元のデカルト座標系のラグランジアンに比べて複雑です。この理由は物理的な意味から来ています。
振り子をつないでいる棒が伸び縮みしないとすると系の自由度は角度\(\theta_1,\theta_2\)の２つです。
となると運動方程式は最高で2本の独立した方程式になるはずです。
しかし、デカルト座標の場合うまく自由度を落とすことができず、運動方程式は4つになってしまいます。
そこで棒が伸び縮みを簡単に表すことができる座標系に移ることでうまく方程式の数を減らせます。

新しい座標系でのラグランジアンで棒の伸び縮みがないという条件を表すには
\(
\begin{align}
r_1&=l_1\ (l_1\mbox{は定数}) \\
r_2&=l_2\ (l_2\mbox{は定数})
\end{align}
\)
と書けるわけで、また、
\(
\begin{align}
\dot{r}_1&=0 \\
\dot{r}_2&=0
\end{align}
\)
となるわけです。

\(m_1=m_2=m,\ l_1=l_2=l\)という場合を特に考えると、ラグランジアンは
\(
\displaystyle L(\theta_1,\dot{\theta}_1,\theta_2,\dot{\theta}_2)=ml^2\left[\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2+\dot{\theta}_1\dot{\theta}_2\cos{(\theta_1-\theta_2)}\right]+mgl(2\cos{\theta_1}+\theta_2)
\)
と書けます。あとはラグランジュの運動方程式を当てはめて計算します。

3, 新たな座標系で運動方程式を導く
保存力場中でのラグランジュの運動方程式は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}_1}\right)-\frac{\partial L}{\partial\theta_1}&=0 \\
\frac{d}{dt}\left(\frac{\partial L}{\partial\dot{\theta}_2}\right)-\frac{\partial L}{\partial\theta_2}&=0
\end{aligned}
\right.
\end{eqnarray}
\)
なので、代入し、\(\ddot{\theta}_1,\ddot{\theta}_2\)に関する運動方程式にすれば
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\ddot{\theta}_1&=\frac{1}{2}\left\{-\ddot{\theta}_2\cos{(\theta_1-\theta_2)}-\dot{\theta}_2^2\sin{(\theta_1-\theta_2)}-2\frac{g}{l}\sin{\theta_1} \right\} \\
\ddot{\theta}_2&=-\ddot{\theta}_1\cos{(\theta_1-\theta_2)}+\dot{\theta}_1^2\sin{(\theta_1-\theta_2)}-\frac{g}{l}\sin{\theta_2}
\end{aligned}
\right.
\end{eqnarray}
\)
となります。これは非線形の２階連立微分方程式です。カオスです。解けません。
数値計算で解きます。用いるのは4次ルンゲ・クッタ法です。

実際に解いてみると、こうなります。

２重振り子の実験もされています。

[adsense2]

カオスが現れる場合、初期値鋭敏性という性質があります。
初期値がほんのちょっと変わるだけでその後の時間発展の様子が大きく変わる性質です。
ちょっと値を変えると上の動画とはまるで違う動きになります。
この動画は上の動画よりも中心に近いほうの粒子の初期速度が4%違います

機械精度の違いでさえも十分な時間発展の後には大きな違いが現れます。複雑であると同時に面白い現象です。

gnuplot

gnuplotで画像出力

コメントする

gnuplotで画像を出力したいことがあります。
その方法を書きたいと思います。

想定する環境

  • gnuplot: Version 4.6 patchlevel 4
  • Imagemagick(convertコマンドを使用)

がインストールされている状況を考えます。特に、gnuplotではdofor構文を用いるため少なくともVersion4.6以上出ないと本稿に沿った画像出力はできませんのでご了承ください。

画像出力について

画像出力するための方法として、epsファイルを出力してからjpgやpng形式に変換します(僕がそれしか知らないためです)。

基本的には
ターミナル(x11とかwxtとかaquaとかpostscriptとかgifとか…)の指定→出力ファイル名の指定→グラフをファイルに出力
という流れになります。
手入力で画像出力する場合はgnuplotで

set terminal postscript eps enhanced color
set output "aaa.eps"
replot

とすれば今出力されているグラフの画像が”aaa.eps”というファイル名で得られます。
もしもjpgやpng形式に変換したければImagemagickのconvertコマンドを用いて、

convert -density 300x300 aaa.eps aaa.jpg

とすればjpg形式が得られます。jpgをpngに書き換えればpngが得られます。

しかし、何枚も画像がほしい場合には不向きです。スクリプトを書きましょう。
“out.plt”というファイルを作り、その中にこう書きます。

fname="$0"
set terminal postscript eps solid enhanced color
set output fname.".eps"
replot
set out
set terminal wxt enhanced

# 1. PNG with background
cv=sprintf("convert -density 300x300 %s.eps %s.png",fname,fname)

# 2. PNG with background
#cv=sprintf("convert -density 150x150 %s.eps %s.png",fname,fname)

# 3. PNG with background white
#cv=sprintf("convert -density 150x150 -background white -flatten -alpha off %s.eps %s.png",fname,fname)

system cv

このファイルをgnuplotのcallコマンドを用いて、

call "out.plt" "bbb"

として呼び出します。callは引数を指定できるコマンドです。
すると”bbb.eps”と”bbb.png”ファイルが作成されます。便利だね!

プログラミングと数値計算

プリクラ問題

コメントする

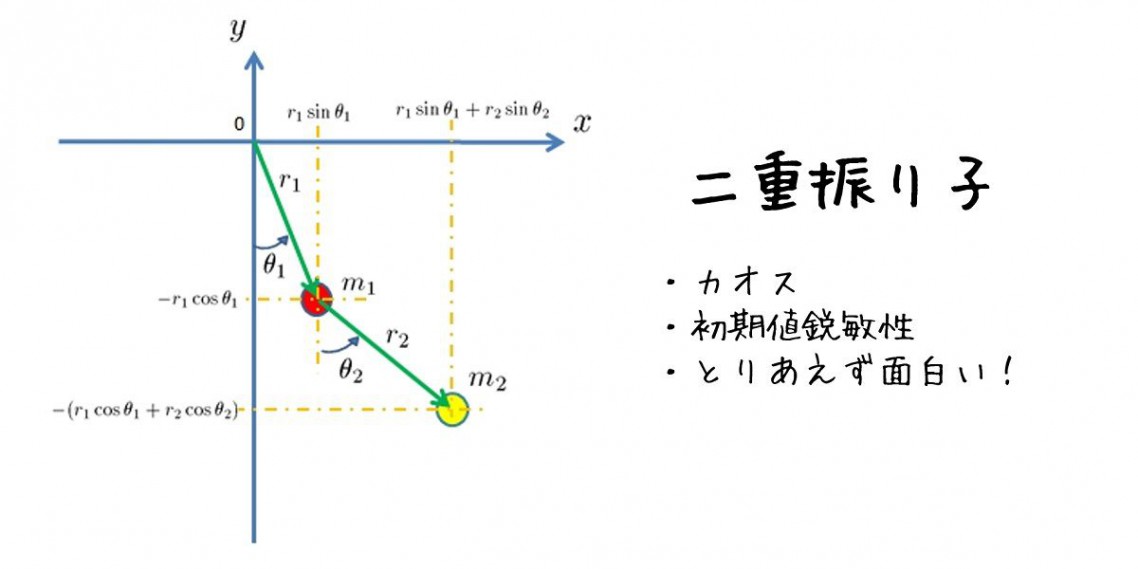
covering designのt=2に相当、
La Jolla Covering Repository Tablesに全部載ってます…
リンク先クリックすればいいんだね。
Combinatorial covering designs に文献とかあるから、なんかもう・・・
もういいや

fortran90によるのコードはこのページの下の方です
だんだんと条件を付け加えて更新していくつもりです。n=9~10でm=3,4程度は厳しいです。

力技でやってみたよ!
主眼が回数になっているので、実際の組み合わせは？と気になってやったものです。

事の発端

コンピュータによる総当たりでは今のままではn=10位が限界です。
だんだんと改良して増やせていければ、と。
コードは後ほど僕に時間ができ次第、公開します。


より↓

念のための確認もかねて、計算は表の値-1から確かめて総当たりを行った結果です。なので具体的な組み合わせが載っているものは正しいはずです。
組み合わせの総数はおおよそ
\(\displaystyle \sum_{q=3}^{q^{Answer}} {}_{{}_nC_m}C_{q}\)
という膨大な数の組み合わせとなります。ここで\(q^{Answer}\)はプリクラ問題の最小回数です。
\(q=3\)はあり得ない、全てを検証する必要はない、など確実にわかる要素は多いですが、例えばn=9,m=3,解q=12を考えると
\(\displaystyle {}_{{}_9C_3}C_{12}=112,992,892,764,570 \ \ \sim 10^{14}(=100T)\)回
の計算が必要です。理想的な状況を考え、cpu10GHz,コア数10で並列処理で行う場合、計算時間は
\(\displaystyle \frac{10^{14}回}{10\times 10^{9}Hz\cdot 10\mbox{コア}}=1000[秒]\)
なのでぎりぎり計算できそうかなーくらいになります。
しかし、このあたりが限界で、n=10,m=3,解q=17になると、
\(\displaystyle {}_{{}_{10}C_3}C_{17}=189,916,591,435,396,829,640\ \ \sim 10^{20}(100E)\)回
の計算となります。先ほどの設定で行うならば、\(10^{9}\)秒~31.7年かかります。
スパコンの京(10PHz)をフルに使えるならば1000[s]で終わります。しかしそこで終わりです。n=11は…もう無理です。

効率のいい方法を考えない限り、解は得られません。

n\m 2 3 4 5 6 7 8 9 10 11
2 1 1 1 1 1 1 1 1 1 1
3 3 1 1 1 1 1 1 1 1 1
4 6 3 1 1 1 1 1 1 1 1
5 10 4 3 1 1 1 1 1 1 1
6 15 6 3 3 1 1 1 1 1 1
7 21 7 5 3 3 1 1 1 1 1
8 28 11 6 4 3 3 1 1 1 1
9 36 12 8 5 3 3 3 1 1 1
10 45 17 9 6 4 3 3 3 1 1
11 55 19 11 7 6 4 3 3 3 1

(3,2)=3

1 2
1 3
2 3

(4,2)=6

略

(4,3)=3

1 2 3
1 2 4
1 3 4

(5,2)=10

略

(5,3)=4

1 2 3
1 2 4
1 2 5
3 4 5

(5,4)=3

1 2 3 4
1 2 3 5
1 2 4 5

(6,2)=15

略

(6,3)=6

1 2 3
1 2 4
1 5 6
2 5 6
3 4 5
3 4 6

(6,4)=3

1 2 3 4
1 2 5 6
3 4 5 6

(6,5)=3

1 2 3 4 5
1 2 3 4 6
1 2 3 5 6

(7,2)=21

略

(7,3)=7

1 2 3
1 4 5
1 6 7
2 4 6
2 5 7
3 4 7
3 5 6

(7,4)=5

1 2 3 4
1 2 3 5
1 2 3 6
1 2 3 7
4 5 6 7
or
1 2 3 5
1 4 6 7
2 3 4 5
2 4 6 7
3 5 6 7

(7,5)=3

1 2 3 4 5
1 2 3 6 7
1 4 5 6 7

(7,6)=3

1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7

(8,2)=28

略

(8,3)=11

計算中…

(8,4)=6

1 2 3 4
1 2 5 6
1 2 7 8
3 4 5 6
3 4 7 8
5 6 7 8

(8,5)=4

1 2 3 4 5
1 2 3 4 6
1 2 3 7 8
4 5 6 7 8

(8,6)=3

1 2 3 4 5 6
1 2 3 4 7 8
1 2 5 6 7 8

(8,7)=3

1 2 3 4 5 6 7
1 2 3 4 5 6 8
1 2 3 4 5 7 8

(9,2)=36

略

(9,3)=12

計算中…

(9,4)=8

1 2 3 5
1 2 3 6
1 2 4 7
1 2 8 9
1 3 4 8
1 3 7 9
4 5 6 9
5 6 7 8


info)cputime=3.0415[s], Nc=10523209, com=1 2 35 115 126

(9,5)=5

1 2 3 4 5
1 2 3 4 6
1 2 7 8 9
3 4 7 8 9
5 6 7 8 9

(9,6)=3

1 2 3 4 5 6
1 2 3 7 8 9
4 5 6 7 8 9

(9,7)=3

1 2 3 4 5 6 7
1 2 3 4 5 8 9
1 2 3 6 7 8 9

(9,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 9
1 2 3 4 5 6 8 9

(10,2)=45

略

(10,3)=17

計算厳しい

(10,4)=9

計算中(4日後くらい?)

(10,5)=6

(10,6)=4

1 2 3 4 5 6
1 2 3 4 7 8
1 2 3 4 9 10
5 6 7 8 9 10

(10,7)=3

1 2 3 4 5 6 7
1 2 3 4 8 9 10
1 5 6 7 8 9 10

(10,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 6 9 10
1 2 3 4 7 8 9 10

(10,9)=3

1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 10
1 2 3 4 5 6 7 9 10

(11,2)=55

略

(11,3)=19

(11,4)=11

(11,5)=7

(11,6)=

(11,7)=4

1 2 3 4 5 6 7
1 2 3 4 5 6 8
1 2 3 4 9 10 11
5 6 7 8 9 10 11

(11,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 9 10 11
1 2 6 7 8 9 10 11

(11,9)=3

1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 10 11
1 2 3 4 5 8 9 10 11

(11,10)=3

1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 11
1 2 3 4 5 6 7 8 10 11


fortran90のコード。総当たりで調べます。
別にinputファイルが必要です。n:m=3:2以上の時は考慮していません。3回で終わるからね。
下の例はn=6, m=3に相当しています。(inputのrはmに相当します。)
qiは調べ始める最低回数、qeは調べ終わる最高回数です。
出力はこうなります。

 M          35
q  -->    3
q  -->    4
q  -->    5
q  -->    6
q  -->    7
 number of calculation     1276464
 cpu_time  0.905050993     [sec]
+------------+
  1  2  3
  1  4  5
  1  6  7
  2  4  6
  2  5  7
  3  4  7
  3  5  6
+------------+

ここからfortran90のコード。gfortranで確かめています。

program main
  implicit none
  integer::n,r,qi,qe,qc
  integer::i,j
  real::t1,t2
  integer,allocatable::groups(:,:)
 
  n=7
  r=3
  qi=3
  qe=10
  allocate(groups(1:qe,1:r))
  groups=0

  call cpu_time(t1)  
  call pkprob(n,r,qi,qe,qc,groups)
  call cpu_time(t2)
  write(6,*)"cpu_time",t2-t1,"[sec]"

  write(6,'(A)')"+------------+"
  do i=1,qc
     do j=1,r
        write(6,'(i3)',advance='no')groups(i,j)
     enddo
     write(6,*)          
  enddo
  write(6,'(A)')"+------------+"
 
  stop
end program main
!==========================
subroutine pkprob(n,r,qi,qe,qc,groups)
  !Covering Design t=2
  implicit none
  integer,intent(in)::n,r,qi,qe
  integer,intent(out)::qc,groups(1:qe,1:r)
 
  integer::q,M,ic,ncalc
  integer::i,j,q2,k
  integer,allocatable::ini(:),tmp(:),cgroup(:,:),pk(:,:)
  integer,allocatable::choose(:)
 
  integer::check1,nCr
  integer::csign
  !  logical::csign,gsign
  external::nCr

  !Combination M=nCr
  M=nCr(n,r)  
  write(6,*)"M",M

  !csign      : Sign of critical combination of array  
  !ic         : Critical value of i which number of combination of combination
  !qc         : Critical value of q which number of combination of combination
  !pk(1:n,1:n): Checking array if every number fill(1) combination or not(0)
  !ncount(1:n): To check calculation number of times
  allocate(ini(1:r),tmp(1:r),cgroup(1:M,1:r))
  ini(1:r)=0
  cgroup(1:M,1:r)=0
  tmp(1:r)=0
 
  do j=1,r
     ini(j)=j
     tmp(j)=ini(j)
  enddo
  !Substitute combination to cgroup.
  do i=1,M
     cgroup(i,1:r)=tmp(1:r)
     call combination(n,r,ini,tmp)
  enddo
  deallocate(ini,tmp)
  !csign      : Sign of critical combination of array  
  !ic         : Critical value of i which number of combination of combination
  !qc         : Critical value of q which number of combination of combination
  !pk(1:n,1:n): Checking array if every number fill(1) combination or not(0)
  !ncount(1:n): To check calculation number of times
  csign=0
  ic=0
  qc=0
  allocate(pk(1:n,1:n))
  pk=0

  ncalc=0

  !q : We need to consider below combination.
  !  Example ) n=5, r=3 case.
  !
  !cgroup(i,1:r)
  !i\r| 1 2 3
  !----------
  ! 1 | 1 2 3
  ! 2 | 1 2 4
  ! 3 | 1 2 5
  ! 4 | 1 3 4
  ! 5 | 1 3 5
  ! 6 | 1 4 5
  ! 7 | 2 3 4
  ! 8 | 2 3 5
  ! 9 | 2 4 5
  !10 | 3 4 5
  !
  !We have to choose q= 3 or 4 or 5 ...combination of "cgroup".
  !Sum total of these combination can write D=_{nCr}C_q.
  !Specifically,
  !---choose q groups from cgroup
  ! +----q=3----+ +-----q=4-----+ +------q=5------+
  ! |choose(1:q)| | choose(1:q) | |  choose(1:q)  |
  ! | l |       | | l |         | | l |           |
  ! |===|=======| |===|=========| |===|===========|
  ! | 1 | 1 2 3 | | 1 | 1 2 3 4 | | 1 | 1 2 3 4 5 |
  ! | 2 | 1 2 4 | | 2 | 1 2 3 5 | | 2 | 1 2 3 4 6 |
  ! | 3 | 1 2 5 | | 3 | 1 2 3 6 | | 3 | 1 2 3 4 7 |
  ! | 4 | 1 2 6 | | 4 | 1 2 4 7 | | 4 | 1 2 3 4 8 |
  ! | 5 | 1 2 7 | | 5 | 1 2 4 8 | | 5 | 1 2 3 4 9 |
  ! | 6 | 1 2 8 | | 6 | 1 2 5 9 | | 6 | 1 2 3 4 10|
  ! | 7 | 1 2 9 | | 7 | 1 2 5 10| | 7 | 1 2 3 5 6 |
  ! |...| . . . | |...| . . . . | |...| . . . .   |
  ! |120| 4 5 6 | |210| 7 8 9 10| |252| 6 7 8 9 10|
  ! +-----------+ +-------------+ +---------------+
  !
  ! If q=4, l=3
  !  We choose below combination, and check satisfy condition or not by "pk".
  ! 1 | 1 2 3
  ! 2 | 1 2 4
  ! 3 | 1 2 5
  ! 6 | 1 4 5
 
  do q=qi,qe
     write(6,'(A,i5)')"q  -->",q
     allocate(choose(1:q),ini(1:q))
     choose(1:q)=0
     ini(1:q)=0
     
     do j=1,q
        ini(j)=j
        choose(j)=ini(j)
     enddo
         
     csign=0
     do while(csign.eq.0)
        !condition 1 to reduce calculation
        check1=cgroup(choose(1),1)
        if(check1.ne.1)exit

        !condition 2 to reduce calculation
        check1=cgroup(choose(2),1)
        if(check1.ge.2)exit

        !condition 3 to reduce calculation for less than n:r=3:2
        check1=cgroup(choose(q),1)
        if(check1.ge.3)then
           pk=0
           do q2=1,q
              do j=1,r
                 do k=1,r
                    pk(cgroup(choose(q2),j),cgroup(choose(q2),k))=1
                 enddo
              enddo
           enddo
           !memory calculation number of times
           ncalc=ncalc+1
           if(minval(pk).eq.1)then
              csign=1
              qc=q
           endif

           if(csign.eq.1)exit
        endif

        !go forward choose(1:q)
        call combination(M,q,ini,choose)
     enddo
     
     if(csign.eq.1)exit
     deallocate(choose,ini)
  enddo
  write(6,*)"number of calculation",ncalc

  groups(1:qe,1:r)=0
  do i=1,qc
     do j=1,r
        groups(i,j)=cgroup(choose(i),j)
     enddo
  enddo
 
  return
end subroutine pkprob
!---------------------------------
subroutine combination(n,r,ini,arr)
  implicit none  
  integer(8)::i,n,r,ini(1:r),bef(1:r),arr(1:r)
  integer(8)::numx
  logical::key(1:r)
 
  bef(1:r)=arr(1:r)-ini(1:r)
  arr(1:r)=0
  key(1:r)=.false.

  numx=n-r
  do i=1,r
     if(bef(i).eq.numx)key(i)=.true.
  enddo

  do i=1,r-1
     if(key(i+1))then
        if(key(i))then
           if(i.ne.1)arr(i)=arr(i-1)      
        else
           arr(i)=bef(i)+1
        endif
     else
        arr(i)=bef(i)
     endif
  enddo
  if(key(r))then
     arr(r)=arr(r-1)
  else
     arr(r)=bef(r)+1
  endif
 
  arr(1:r)=arr(1:r)+ini(1:r)

  return
end subroutine combination
!----------------------------------
function nCr(n,r)
  implicit none
  integer(8)::n,r,i,r0,nCr

  r0=n-r
  if(r.le.r0)r0=r

  nCr=1
  do i=1,r0
     nCr=nCr*(n-r0+i)
     nCr=nCr/i
  enddo
 
  return
end function nCr
Linux

LXDE

1件のコメント

LinuxMint 17.1 “Rebecca” においてデスクトップ環境”lxde”をインストールするための手順です。

LXDEの導入

lxdeとは?
→Arch Linux LXDE (日本語)より引用

LXDE (“Lightweight X11 Desktop Environment”) は極めて高いパフォーマンスを持ち省エネルギーなデスクトップ環境です。開発者たちの国際的なコミュニティにより管理され、美しいインターフェース、多言語対応、標準的なキーボードショートカットとタブファイラーのような追加機能を含みます。LXDE は CPU も RAM も他のデスクトップ環境に比べ消費が少ないです。特に、ネットブック、モバイル端末や、古い計算機などによるクラウドコンピューティングにあわせてデザインされています。

ぶっちゃければ軽いよ！ということです。
windowsだったらこの変更に相当する操作はありません。
これからやろうとしているのは
OS → バージョン → デスクトップ環境
の順で書けば、
LinuxMint → 17.1(Rebecca) → cinnamon
から
LinuxMint → 17.1(Rebecca) → LXDE
に変更する、という操作です。cinnamon, LXDEの他にMate, KDE, Xfceなどがあります。
詳しくは調べてください。

設定→Synapticパッケージマネージャ
と進みます。
Synapticパッケージマネージャの検索ボックスでlxdeを検索してチェック、チェックして出てくる関連のものも全てチェックします。
さらに、lxdmもチェックします。
どうやらこのlxdmがないとログイン画面でどのデスクトップ環境でスタートするか？の選択ができません。

あとはSynapticパッケージマネージャの”適用”を押せば終了です。ログアウトして、
ログイン画面で(多分デフォルトでは)λになっているところを押してlxdeで起動を選択、その後ログインしましょう。

lxterminal のカラーを変えたい！

　 …できません。

Thread: Colour Scheme on lxterminal in lubuntu
と
LXTerminal Colors?
より。

At this time we do not offer any more customization than foreground/background. You are encouraged to run any terminal emulator that meets your needs.

訳すと、”前景色と背景色以上のカスタマイズは提供しないよ。カスタムしたかったら別のターミナルをインストールしてねミ☆”
だそうです。

→guake terminalというのがよさそうです。

sudo apt-get install guake

で、インストールが終わったら端末で

guake

と入力し、F12キーを押せば立ち上がります。guake terminalの設定は
スタートボタン→設定→Guake Preferences
で設定できます。

LXDEのスタートアップ(起動時に自動的に実行させるプログラム)の設定がないよ！

Arch LXDEによると、
ディレクトリの場所：~/.config/lxsession/LXDE/autostart
にLXDEを起動させたときに実行させるプログラムが書いてあります。その中身に何が書いてあるかというと、

@xscreensaver -no-splash
@lxpanel --profile LXDE
@pcmanfm --desktop --profile LXDE
@/usr/lib/policykit-1-gnome/polkit-gnome-authentication-agent-1

のような文が記述されていると思います。意味はArch LXDEによると@以下の文が起動時のプログラムとして実行されます。
なので、ここを書き換えて、たとえばguake端末を起動時に立ち上げたいのならば

@xscreensaver -no-splash
@lxpanel --profile LXDE
@pcmanfm --desktop --profile LXDE
@/usr/lib/policykit-1-gnome/polkit-gnome-authentication-agent-1
@guake

という風に@guakeを付け加えてあげましょう。

guakeの横幅を変えたいよ！

How To Adjust Guake Terminal Width を見てみるとUbuntu12.10以降はguakeの設定ファイルは

/usr/bin/guake

にあります。LinuxMint17.1でも同じで、上のディレクトリにあります。この中身を編集していきます。

sudo emacs /usr/bin/guake

で開き、820~830行目あたりにある

def get_final_window_rect(self):
    """Gets the final size of the main window of guake. The height
    is the window_height property, width is window_width and the
    horizontal alignment is given by window_alignment.
    """
    screen = self.window.get_screen()
    height = self.client.get_int(KEY('/general/window_height'))
    width = 100
    halignment = self.client.get_int(KEY('/general/window_halignment'))

のwidth=100になっているところ書き換えてwidth=50とか80とかにします。
ちなみにこのwidthはウインドウの横幅に対するパーセンテージです。

※サイトで検索した時、下の場所にあるからねーっていう記述がかなりあったけれどこれはUbuntu12.04以前の場合です。
/usr/lib/guake/guake.py
昔のだね。

テキストエディタ, プログラミングと数値計算

フォントサイズ変更

コメントする

emacsでフォントサイズを変更したい場合は？環境はemacs24。

(調べてもよくわからないし出てこない…。)
一度だけ変更したい場合は、Ctrl-x-± で可能です。
ではずっと変更したい場合は？
emacsの設定ファイルに記述します。emacsの設定ファイルの場所は
emacswiki – InitFileより

  1. For GnuEmacs, it is ~/.emacs or _emacs or ~/.emacs.d/init.el.
  2. For XEmacs, it is ~/.xemacs or ~/.xemacs/init.el.
  3. For AquamacsEmacs, it is ~/.emacs or ~/Library/Preferences/Aquamacs Emacs/Preferences.el

にあります。環境によって場所が異なります。
Linuxmint17.1,”sudo apt-get install emacs24″で行った場合、おそらく~/.emacsでしょう。

21.8 Fontsを見るとデフォルトでは
フォント(の種類) : monospace font
フォントサイズ : 10pt
として設定されているそうです。

テキストエディタで~/.emacsを開き、
(custom-set-variables
…
…
)
の括弧の外に

(add-to-list 'default-frame-alist
                       '(font . "DejaVu Sans Mono-12"))

という文を記述します。
現在、フォントのタイプの変更は僕は分かりません。多分DejaVu…を変えればよさそう。
12のところを10とか14とかに変えればデフォルトのフォントサイズを変更することができます。

見出しに使っている画像は8,9,10,11,12,20の場合の比較です。参考にどうぞ。

僕の使ってる~./emacsはこちら

gnuplot

カラーマップの上に線を描く

コメントする

gnuplotでカラーマップの上に2次元で書かれたグラフを書きたいとします。

この場合は

set pm3d map
splot "fort.11" u 1:2:3 with pm3d, "fort.10" u 1:2:($2-$2) with point

とすればokです。
カラーマップの情報はfort.10, 書きたい線のデータはfort.11に書かれているとします。
考えは、2次元のデータをあたかも3次元のデータとして扱うことで解決します。

coloronplot
上のデータを得るためのfortranコードはこんな感じです。

program main
  implicit none
  double precision::x,y,h
 
  h=5.d-2
  y=-3.d0
  do while(y.le.3.d0)
     x=-3.d0
     do while(x.le.3.d0)
        write(11,*)x,y,x+y
        x=x+h
     enddo
     write(11,*)
     
     write(10,*)y,sin(y)
     y=y+h
  enddo

  return
end program main

818 re(1):pm3dによる等高線図（カラーマップ）に2次元グラフを重ねる方法

プログラミングと数値計算

組み合わせ

2件のコメント

組み合わせ\(_nC_r\)、重複組み合わせ\(_nH_r\)の一覧を求めるfortranコードです。

\(_nH_r=~_{n+r-1}C_r\)


組み合わせ\(_nC_r\)の場合

  1  2  3  4
  1  2  3  5
  1  2  3  6
  1  2  4  5
  1  2  4  6
  1  2  5  6
  1  3  4  5
  1  3  4  6
  1  3  5  6
  1  4  5  6
  2  3  4  5
  2  3  4  6
  2  3  5  6
  2  4  5  6
  3  4  5  6

を得たい場合

重複組み合わせ\(_nH_r\)の場合

  1  1  1  1
  1  1  1  2
  1  1  1  3
  1  1  2  2
  1  1  2  3
  1  1  3  3
  1  2  2  2
  1  2  2  3
  1  2  3  3
  1  3  3  3
  2  2  2  2
  2  2  2  3
  2  2  3  3
  2  3  3  3
  3  3  3  3

を得たい場合

組み合わせをrecursionを使わないで得るために、全ての行を初めの値で引いてみました。

+------------+
  0  0  0  0
  0  0  0  1
  0  0  0  2
  0  0  1  1
  0  0  1  2
  0  0  2  2
  0  1  1  1
  0  1  1  2
  0  1  2  2
  0  2  2  2
  1  1  1  1
  1  1  1  2
  1  1  2  2
  1  2  2  2
  2  2  2  2
+------------+

すると、ちょうどr進数と同じになります。なので、これを復元するプログラムを書きました。

プログラミングと数値計算

時間計測

4件のコメント

fortran90において、
このプログラムは何秒かかるか？
早い？遅い？
を調べるためにはもちろん計算時間を計るのが一番です。

  1. 実時間とCPU時間の違い
  2. 実時間計測
  3. CPU時間計測

実時間とCPU時間の違い

『計算時間』には大きく２種類あります。実時間とCPU時間です。

  • 実時間 → 現実の世界での経過時間
  • CPU時間 → プログラムの実行でCPUを使った時間

※[1]より。参考文献とは程遠いですが、僕の認識とあっていて、綺麗な説明と感じたので載せておきます。

例えば、計算時間はそんなにかかってないのに詳細な画像を得たいがために書き出すデータ量を増やしている場合、実時間は長く、CPU時間は短くなります。
また、あるデータ点1つを得るために計算時間は膨大にかかる場合、実時間≈CPU時間になります。

fortranでは時刻を得るためのサブルーチンが既に用意されています。
ここで紹介するのは、実時間を得るための
date_and_time
と
system_clock
の2種類。
CPU時間を得るためのサブルーチンは
cpu_time
の1種類です。

実時間計測(date_and_time)

その場所で何時何分何秒を出力させたい時、その場所に

  write(6,'(3A,i0,A,i0,A,i0,A,i0,A,i0,A,i0,A)')"  == ", &
       c," ",ti(1),"/",ti(2),"/",ti(3), &
       "  ",ti(5),":",ti(6),":",ti(7),", (yyyy/mm/dd  hh:mm:ss)"

を入れましょう[2]。character(10)::b(1:3), integer::ti(1:8)です。

使う際はこうすると良いでしょう。

program main
  implicit none

  call current_time("program start ")  

  !program here
  write(6,*)"press Enter"
  read *
   
  call current_time("program finish")  
 
  stop
end program main

subroutine current_time(c)
  implicit none
  character(*),intent(in)::c
  integer::ti(1:8)
  character(10)::b(1:3)
 
  call date_and_time(b(1),b(2),b(3),ti)
  write(6,*)
  write(6,'(3A,i0,A,i0,A,i0,A,i0,A,i0,A,i0,A)')"  == ", &
       c," ",ti(1),"/",ti(2),"/",ti(3), &
       "  ",ti(5),":",ti(6),":",ti(7),", (yyyy/mm/dd  hh:mm:ss)"
  write(6,*)
 
  return
end subroutine current_time

サブルーチンcurrent_timeを定義して、それを呼び出すだけのほうが分かりやすいかと思います。
引数は何という文言をその場所に指定したいかを示すものです。
実行して適当なときにEnterキーを押してプログラムを進めると、

$ gfortran main2.f90
$ ./a.out
   
  == program start  2016/2/15  9:16:38, (yyyy/mm/dd  hh:mm:ss)

 press Enter

  == program finish 2016/2/15  9:16:40, (yyyy/mm/dd  hh:mm:ss)

$

という結果が得られるでしょう。もちろん、プログラムを動かした時点での時間が表示されます。
一瞬で終わるプログラムの場合は差は見られ無いと思います。

実時間計測(system_clock)

system_clockはfortran標準実装なので汎用性は高いです[4]。system_clockは組み込まれているサブルーチンなので下のプログラムをそのままコピペして使う事が出来ます。

program main
  implicit none
  integer::ti,tf,tr ! ti: initial time, tf: finish time, tr: time rate
  integer::i

  call system_clock(ti)

  !program here
  write(6,*)"press Enter"
  read *

  call system_clock(tf,tr)
 
  write(6,'(f10.3,A)')(tf-ti)/dble(tr),"[s]"
 
  return
end program main

上の文を実行して適当なときにEnterキーを押してプログラムを進めると、

$ gfortran main2.f90
$ ./a.out
    press Enter
      1.283[s]
$

という出力が得られます。

CPU時間の計測(cpu_time)

CPU時間の計測するには

    call cpu_time(t0)
    ...
    call cpu_time(t1)
    write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"

を入れましょう[3]。real::t1,t2です。

program main
  implicit none
  real::t0,t1
  integer::i

  call cpu_time(t0)

  !program here
  write(6,*)"press Enter"
  read *
 
  call cpu_time(t1)
 
  write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"
 
  stop
end program main

でokです。適当な時間待って、Enterキーを押すと

$ gfortran main2.f90
$ ./a.out
    press Enter
     0.000[s]

という出力が得られるでしょう。
これはcpuを動かしていないためであり、cpuが動いていた時間というのは限りなく0だ、ということです。

参考文献

[1]ユーザ時間とシステム時間の違いを教えてください。
[2]1.4.7.1 date_and_time: 日付と時刻の取得 -ORACLE®
[3]8 移植性のある時間計測の方法 -nag
[4]9.254 SYSTEM_CLOCK — Time function

プログラミングと数値計算

大きな数を扱う

2件のコメント

大きい数＝工夫or対数!

大きい数を扱う…例えば階乗を計算しろ、という問題や組み合わせ\(_nC_r\)を計算しろ、という問題に時々あたります。

まず、典型的な例として組み合わせ
\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)
を計算しましょう。
この計算はそのまま定義のまま計算しようとすると階乗が出てくるので、途中の値は物凄くでかい数字になるのですが、最後の答えは小さい値になるはずです。それなのに計算できないのはおかしくない!?工夫次第で何とかなるものです。
下の表は３つの計算方法についてまとめたものです。

integer(4バイト整数型±2 147 483 647)を用いた計算
定義のまま計算 工夫して計算 対数を利用して計算
最大のn,r \(_{12}C_6\) \(_{29}C_{14}\) \(_{33}C_{16}\)
理由 階乗の計算によるオーバーフロー “割り切れる”ための制約 (限界値)

integer(8バイト整数型±9 223 372 036 854 775 807)を用いた計算
計算方法 定義のまま計算 工夫して計算 対数を利用して計算
最大のn,r \(_{20}C_{10}\) \(_{61}C_{30}\) \(_{48}C_{24}\)
理由 階乗の計算によるオーバーフロー “割り切れる”ための制約 倍精度型変数の有効桁数が足りない
定義のまま計算

例えばfortranでintegerの宣言により定義した場合、階乗が正しく計算できる範囲(オーバーフローしない範囲)は、\(12!=479\ 001\ 600\)
まで計算できます。
変数の型がいくつまで計算できるかは、組み込み関数hugeを使うことで確認できます。

program main
  implicit none
  integer::n

  write(6,*)"huge",huge(n)

  stop
end program main

これで確認すると、整数型は
\(\pm 2\ 147\ 483\ 647\)
までの値なら代入することができるため、
\(13!=6\ 227\ 020\ 800\)は計算できないことがわかります。
一応関数はこんな感じ。

function nCr_fact(n,r)
  !sikinote
  implicit none
  integer::nCr_fact,fact,n,r
  external::fact
 
  nCr_fact=fact(n)/(fact(n-r)*fact(r))
 
  return
end function nCr_fact
function fact(n)
  implicit none
  integer::fact,i,n
 
  if(n.le.-1)write(6,*)"####warning#### parameter of factorial has negative value"
  fact=1
  do i=2,n
     fact=fact*i
  enddo

  return
end function fact

( ※余談ですが、8バイト型整数で宣言、すなわちinteger(8)で宣言すると
\(9\ 223\ 372\ 036\ 854\ 775\ 807\)
まで計算できます(19桁、\(20!=2\ 432\ 902\ 008\ 176\ 640\ 000\)まで)。)

なので定義通りの計算はn=12までが限界です。実用的じゃありません。

工夫して計算

\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)を工夫します。

\(
\begin{align}
\displaystyle _nC_r&=\frac{n!}{(n-r)!r!} \\
&=\frac{n(n-1)(n-2)\cdots(n-r+2)(n-r+1)}{r(r-1)(r-2)\cdots2\cdot 1} \\
&=\frac{n}{r}\cdot \frac{n-1}{r-1}\cdot \frac{n-2}{r-2}\cdots \frac{n-r+2}{2}\cdot \frac{n-r+1}{1} \\
&=\prod_{i=1}^r\frac{n-r+i}{i}
\end{align}
\)
として計算します。こうすれば階乗みたいに大きな数を計算する必要がなくなります。
関数を書けばこうなります。

function nCr(n,r)
  !sikinote
  implicit none
  integer::n,r,i,r0,nCr

  r0=n-r
  if(r.le.r0)r0=r

  nCr=1
  do i=1,r0
     nCr=nCr*(n-r0+i)
     nCr=nCr/i
  enddo
 
  return
end function nCr

で\(_nC_r\)を求めることができます。
上のプログラムでは、最大\(_{29}C_{14}=77\ 558\ 760\)まで求めることができます。
これは絶対に割り切れることを前提にしているためにおこるもので、

nCr=nCr*(n-r0+i)

の文のところで最大値が決まってしまうためです。
定式化すれば、
式\(_nC_r\)に対し、\(_{n-1}C_{r-1}\cdot n\)が扱える整数値を超えないこと
と表現できます。

\(_{29}C_{14}=77\ 558\ 760\)が計算できるのは、
\(_{29-1}C_{14-1}*29=1\ 085\ 822\ 640\)
であるので計算可能です。次の\(_{30}C_{15}\)を計算するためには
\(_{30-1}C_{15-1}*30=2\ 326\ 762\ 800\)が
integerの最大の整数値\(\pm 2\ 147\ 483\ 647\)
を超えてしまうのでこれ以上計算はできません。
※もしもinteger(8)を用いると\(_{61}C_{30}\)まで計算できます。

対数を利用して計算

もう一つ対数を利用した方法を紹介します。
対数を利用すると、
\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)は、\(S= _nC_r\)とおくと
\(
\begin{align}
\displaystyle \ln(S)&=\ln\left[\frac{n!}{(n-r)!r!}\right] \\
&=\ln(n!)-\ln\{(n-r)!\}-\ln(r!) \\
&=\sum_{i=n-r+1}^n\ln(i)-\sum_{i=2}^{r}\ln(i)
\end{align}
\)
と書けます。よって、
\(\displaystyle S=\exp\left[\sum_{i=n-r+1}^n\ln(i)-\sum_{i=2}^{r}\ln(i)\right]\)
です。プログラムを書けば

function nCr_log(n,r)
  !sikinote
  implicit none
  integer::n,r,i,r0,nCr2
  double precision::tmp
 
  r0=n-r
  if(r.le.r0)r0=r

  tmp=0.d0
  do i=n-r0+1,n
     tmp=tmp+log(dble(i))
  enddo
  do i=2,r0
     tmp=tmp-log(dble(i))
  enddo

  nCr2=nint(exp(tmp))  

  return
end function nCr_log

となります。この場合は\(_{n}C_{r}\)が整数型で扱える範囲を越えなければいいという条件だけになるので、
integerでは\(_{33}C_{16}\)までokです。

integer(8)では\(_{66}C_{33}\)までできます…が、上のプログラムそのままではできません。
おそらく、組み込み関数nint(実数型を整数型に四捨五入して代入する)がinteger(8)に対応していない(かも)ということと、倍精度の有効桁数がだんだんと足らなくなっていくので厳しいです。後者による問題によって、確認した範囲では\(_{48}C_{24}\)位が限界です。