sikino のすべての投稿

物理学

時間発展演算子の導出

5件のコメント

量子力学における時間発展演算子\(\displaystyle \hat{U}_{(t)}=e^{-i\frac{\hat{H}}{\hbar}t}\)の導出です。
これは、ハミルトニアンは時間依存しない場合に限ります。時間依存するときは時間順序積という概念が出てきます。

シュレディンガー方程式
\(
\begin{align}
i\hbar\frac{\partial}{\partial t}\psi_{(x,t)}=\hat{H}\psi_{(x,t)}
\end{align}
\)
は既知のものとして進めます。

形式的な導出でよく説明されるのは以下の手順です。

シュレディンガー方程式の両辺を\(i\hbar\)で割って、更に波動関数\(\psi_{(x,t)}\)で割り両辺を時刻\(0\sim t\)まで積分します。
すなわち、
\(
\begin{align}
\int_{\psi_{(0)}}^{\psi_{(t)}}\frac{d\psi}{\psi}&=\int_0^t\frac{\hat{H}}{i\hbar}dt^{\prime} \\
\ln\frac{\psi_{(t)}}{\psi_{(0)}}&=\frac{-i}{\hbar}\hat{H}t \\
\end{align}
\)

なので
\(
\displaystyle \psi_{(x,t)}=e^{-i\frac{\hat{H}}{\hbar}t}\psi_{(x,0)}
\)
証明終了,,

(;’;ﾟ;ж;ﾟ;｀;)ﾌﾞﾎｫｯ
(; ^ω^)は…

何で波動関数で割ってくれちゃってるんですか？ハミルトニアンは演算子ですよ。形式的にしてもひどくない？

ということで、ちゃんと求めましょう。結果は↑のものと同じになります。不思議ですね。

ハミルトニアンが時間依存しないという条件の下求めます。
まず、時間依存するシュレディンガー方程式より、
\(
\displaystyle i\hbar\frac{\partial}{\partial t}\psi_{(x,t)}=\hat{H}\psi_{(x,t)}
\)
となります。無限小時間\(\Delta t\)に対して、シュレディンガー方程式は、
\(
\displaystyle i\hbar\lim_{\Delta t\rightarrow 0}\frac{\psi_{(x,t+\Delta t)}-\psi_{(x,t)}}{\Delta t}=\hat{H}\psi_{(x,t)}
\)
です。以降\(\lim\)は省略します。

式を変形して、
\(
\displaystyle \psi_{(x,t+\Delta t)}=\left(1-i\frac{\hat{H}}{\hbar}\Delta t\right)\psi_{(x,t)}
\)
また、もう\(\Delta t\)だけ時間を進めると、
\(
\displaystyle \psi_{(x,t+2\Delta t)}=\left(1-i\frac{\hat{H}}{\hbar}\Delta t\right)^2\psi_{(x,t)}
\)
という結果が得られます。

ここで、\(\Delta t\)をN回作用させることを考えます。
すなわち、\(t^{\prime}=N\Delta t\)とおき、\(\Delta t=\frac{t^{\prime}}{N}\)として考えれば、任意の時間\(t^{\prime}\)に対して、
\(
\displaystyle \psi_{(x,t+t^{\prime})}=\left(1-i\frac{\hat{H}}{\hbar}t^{\prime}\frac{1}{N}\right)^N\psi_{(x,t)}
\)
という式が成立します。

無限回、微小区間\(\Delta t\)を動かす操作を考えればいいので、\(N\rightarrow \infty\)として考えれば、
\(
\displaystyle \psi_{(x,t+t^{\prime})}=\lim_{N\rightarrow \infty}\left(1-i\frac{\hat{H}}{\hbar}t^{\prime}\frac{1}{N}\right)^N\psi_{(x,t)}
\)
公式
\(
\displaystyle \lim_{x\rightarrow \pm\infty}\left(1+\frac{a}{x}\right)^x=e^a
\)
より、
\(
\displaystyle \psi_{(x,t+t^{\prime})}=e^{-i\frac{\hat{H}}{\hbar}t^{\prime}}\psi_{(x,t)}
\)

\(t=0\)と置き、\(t^{\prime}=t\)と文字を置き換えれば、
\(
\displaystyle \psi_{(x,t)}=e^{-i\frac{\hat{H}}{\hbar}t}\psi_{(x,0)}
\)

となり、ちゃんと時間発展演算子が導けました。めでたしめでたし。

ハミルトニアンが時間依存する場合、
\(
\displaystyle i\hbar\frac{\partial}{\partial t}\psi_{(x,t)}=\hat{H}_{(t)}\psi_{(x,t)}
\)
となります。無限小時間\(\Delta t\)に対して、シュレディンガー方程式は、
\(
\displaystyle i\hbar\lim_{\Delta t\rightarrow 0}\frac{\psi_{(x,t+\Delta t)}-\psi_{(x,t)}}{\Delta t}=\hat{H}_{(t)}\psi_{(x,t)}
\)
次の時刻では
\(
\displaystyle \psi_{(x,t+2\Delta t)}=
\left(1-i\frac{\hat{H}_{(t+\Delta t)}}{\hbar}\Delta t\right)\left(1-i\frac{\hat{H}_{(t)}}{\hbar}\Delta t\right)\psi_{(x,t)}
\)
となります。２乗にはなってくれません。
と、どんどん作用させていくわけです。時間依存しない時と明らかに違ったものになりますが、詳しくは次の機会のお話で。

プログラミングと数値計算, ルンゲ=クッタ法

ルンゲ=クッタ法の説明と刻み幅制御

5件のコメント

ルンゲ=クッタ法(Runge-Kutta method、RK法)とは?
僕の知る限りの知識で紹介します。

特に良く使われる陽的ルンゲ=クッタ法は、
・実装が簡単
・良いアルゴリズムではない
という手法です。

良いアルゴリズムである陰的ルンゲ=クッタ法は、
陰的ルンゲ=クッタ法
をご覧ください。

もくじ

  1. ルンゲ=クッタ法の系統
  2. 陽的ルンゲ=クッタ法の段数と次数について
  3. 誤差について
  4. Butcher tableによるルンゲ=クッタ法の記述
  5. 埋め込まれた陽的ルンゲ=クッタ法
  6. ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(適応刻み幅制御)
  7. ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御のプログラム(実数/複素数 で １/２ 階微分方程式を解くプログラム)
  8. 不連続な点を含む場合
  9. 刻み幅制御のベンチマーク(振り子)
  10. （追記）ルンゲ=クッタ=ドルマンド=プリンス法
  11. 陽的ルンゲ=クッタ法の導出
  12. 参考文献

理論はいいから4次ルンゲ=クッタ法の数値計算ではどうやるかだけ教えてくれ！という方は4次ルンゲ=クッタ法へどうぞ。

ルンゲ=クッタ法の系統

ルンゲ=クッタ法は微分方程式の数値計算解を得るための手法のことを指します。

通常の参考書で微分方程式を解くために良く紹介されているのは、オイラー法と中点法、４次ルンゲ=クッタ法でしょうか。
オイラー法も中点法も4次ルンゲ=クッタ法も、”陽的ルンゲクッタ法” と呼ばれる枠組みの1つです。

オイラー法は正確には “陽的1段1次ルンゲ=クッタ法” と呼ばれ、
中点法は “陽的2段2次ルンゲ=クッタ法”、
4次ルンゲクッタ法(RK4)は、”陽的4段4次ルンゲ=クッタ法” と呼ばれています。

“段”と”次”とはなんなんでしょう？それは、
計算の大変さ(段)と、計算の正確さ(次)
です。”段“の値が小さければ小さいほど計算時間が少なくて済みますし、”次“の値が高ければ高いほど計算が正確です。

オイラー法は1という計算コストで正確さ1が得られますし、RK4は4という計算コストで正確さ4が得られます。

4次ルンゲ=クッタ法が使われる理由

理由は実装が簡単でそれなりの精度を持つから。です。

陽的ルンゲ=クッタ法において、pという計算コスト(p段)で、pより大きな正確さq(q次)を得ることはできません。
Derivation of Runge–Kutta methodsによれば、
\(q\)次の正確さ(q次のオーダー)を得たい場合、最低限必要な段数\(p_{\mbox{min}}(q)\)は

という関係にあります。

ここで注目するべきは4次の時までは計算コストに比例して計算精度が上がっていきます。
しかし、4次以上では、計算コストの増加と計算の正確さが見合わなくなっていきます。故に
計算効率が良いのは4次だろう、
と予想できます。
また、重要な理由として、4次ルンゲ=クッタ法に現れる係数が5次以降と比べて圧倒的にシンプルであることが挙げられます。4次では\(0,1/2,1/6\)程度の係数だけが使われ、プログラム作成時の入力ミスがほぼ生まれません。しかし、5次では\(28561/56430, -7200/2197\)といった係数が数多く出てきます。
これらの理由から,4次ルンゲ=クッタ法(RK4)が数値計算科学の世界でよく使われるのです。

陽的ルンゲ=クッタ法に限って言えばプログラムの実装が非常に簡単であることが挙げられます。陰的ルンゲ=クッタ法と呼ばれるアルゴリズムもあり、これは陽的ルンゲ=クッタよりも優れていますが、計算量が多くなり、若干複雑なアルゴリズムになります。陰的ルンゲ=クッタ法を詳しく知りたい方は陰的ルンゲ=クッタ法をご覧ください。

Q. オイラー法もものすごく細かい分点を取れば、その計算効率はRK4と同じなんじゃないの？
A. 刻み幅の乗数で効いてくるのでそうではありません。高次を使っても計算が信頼できるのであれば、大きなステップで進めるほうが早いです。例え、目標精度への計算時間が同じだとしても、計算機の有効桁数によって否定されてしまいます。
RK4で典型的にとられる時間ステップの間隔は、おおよそ\(10^{-2}\sim 10^{-4}\)程度であり、RK4のエラーのオーダーは\(O(h^5)\)です。
そして、科学計算で使う際の有効桁数は倍精度型で16桁です。
1ステップ当りの誤差は\(h\)の減少に伴い、解が\(h^4\)の早さで収束していく、と言えます。
だから16桁の計算では\(h=10^{-1}\to h=10^{-4}\)に変化させる時、誤差は\(O(h^5)=c 10^{-5}\to c 10^{-20}\)と変化します。
おおよそ\(c\approx 1\)と見積もれば、(有効桁数16桁を多少超えてしまいますが、)有効桁数いっぱいまで正しい値が出るであろうと期待できます。

これに対し、オイラー法で同じことをするには\(h\)を\(10^{-16}\)にしなくてはいけません。
\(t\)の値が\(10^{-16}\)変わった時に、桁落ちの問題を回避できるほど関数\(x\)の値に変化が生まれるか？
が問題になり、まぁそんな急激な変化は生まれないでしょう、と予想できます。これでは桁落ちの問題を回避するほどの変化は到底望めません。

よって計算の効率と有効桁数の限界から、RK4なのです。

また、あまりに高次の方法を使うとルンゲ現象に代表される不安定性といったことが起こるかもしれません。
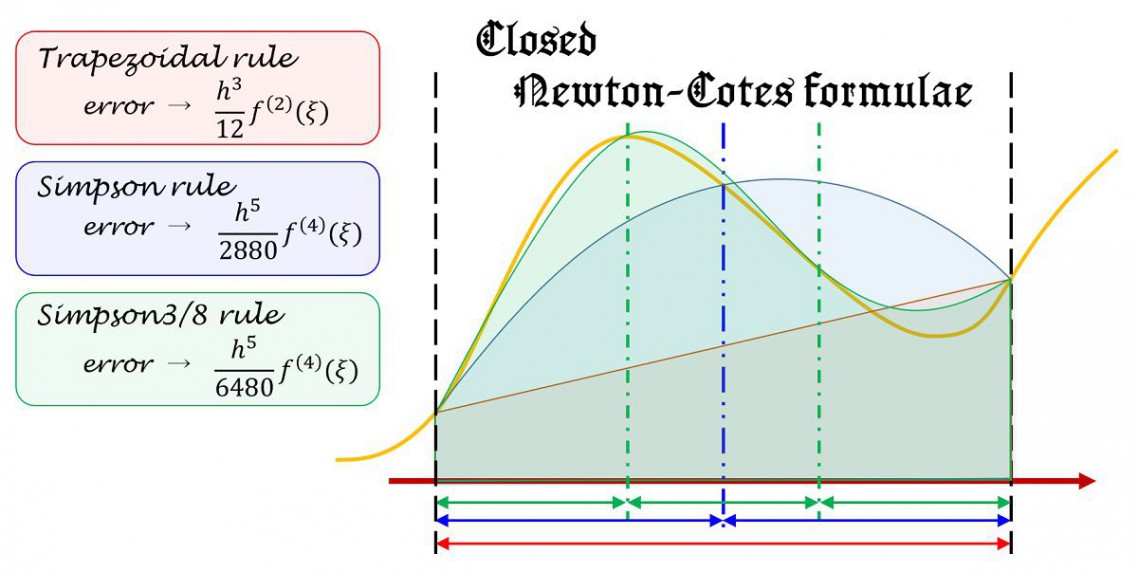
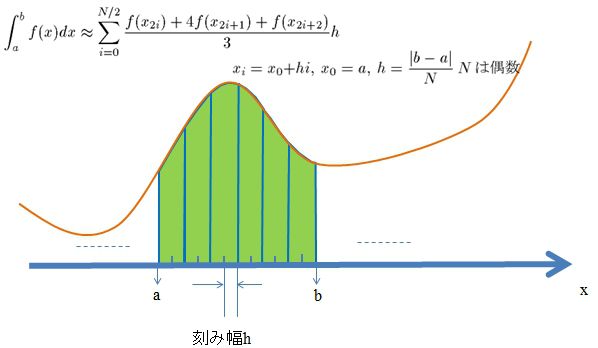
高次は高精度という意味とイコールではないことに注意しましょう。この高次≠高精度については等間隔の分点における数値積分の時に書いたので気になる方はどうぞ。。

誤差について

4次ルンゲ=クッタ法の、1ステップ当りの誤差は\(h^5\)に比例,すなわち\(O(h^5)\)です。
しかし、通常は細かいルンゲ=クッタ法を何度も繰り返して計算します。
区間\([a,b]\)を刻み幅\(h\)の4次ルンゲ=クッタ法で\(N\)回のステップを繰り返し計算する場合、誤差は
\(
\displaystyle N\cdot O(h^5)=\frac{b-a}{h}\cdot O(h^5)=O(h^4)\)

となります。よって、\(N\)回繰り返すような計算では、オーダーが１つ落ちる事に注意しましょう。

[adsense1]

陽的ルンゲ=クッタ法の段数と次数について

さて、ここまで“段”は計算コスト、で“次”は計算の正確さ、という曖昧な表現でしたが、その表現をちゃんと知りましょう。
段と次を知るためにはルンゲ=クッタ法の計算方法を知る必要があります。
具体例を載せます。
\(
\displaystyle \frac{dx}{dt}=f(t,x)
\)
の、\(t_{n}\rightarrow t_{n}+h\ \ (=t_{n+1})\)における初期値問題に対する、
陽的1段1次ルンゲ=クッタ法(オイラー法)の計算スキームは、
\(
x_{n+1}=x_{n}+h\cdot f(t_{n},x_{n})
\)
です。

陽的4段4次ルンゲ=クッタ法(RK4)の計算スキームは、
\(
\begin{align}
k_1&=f(t_n, x_n) \\
k_2&=f(t_n+h/2, x_n+h k_1/2) \\
k_3&=f(t_n+h/2, x_n+h k_2/2) \\
k_4&=f(t_n+h, x_n+h k_3) \\
x_{n+1}&=x_{n}+{(k_1+2k_2+2k_3+k_4)}h/6
\end{align}
\)
として与えられます。

一般的に、陽的s段のルンゲ=クッタ法とは
\(
\begin{align}
g_i&=x_n+h\sum_{j=1}a_{i,j}k_j\ \ \ (j\lt i, \ i=1,2,…,s) \\
k_i&=f(t_n+c_ih, g_i) \\
x_{n+1}&=x_n+h\sum_{i=1}^s b_ik_i
\end{align}
\)
として書けます。
ここで行列形式で与えられる係数\(a_{i,j}, b_{i},c_{i}\)によって、そのs段ルンゲ=クッタ法が持つ次数が決められます。段数はここから由来します。

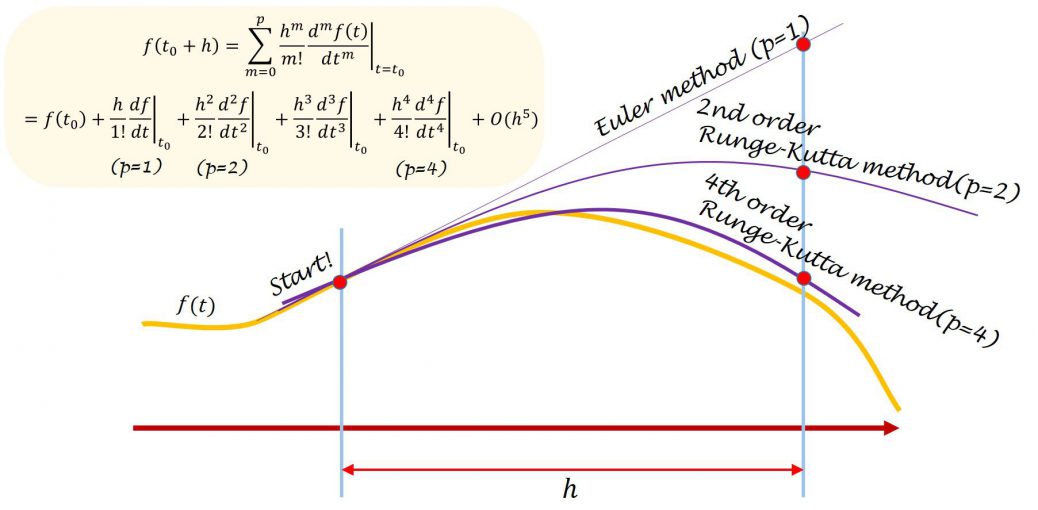
点\((t_n, x(t_n))\)周りで関数をテーラー展開し、その関数が点\((t_n+h\ \ (=t_{n+1}), x(t_{n+1}))\)で作る点を近似解とするのがルンゲ=クッタ法です。
故に、\(x(t_{n+1})\)は、
\(
\begin{align}
x(t_{n+1})=x(t_n)+\left.\frac{h}{1!}\frac{dx}{dt}\right|_{t=t_n}+\left.\frac{h^2}{2!}\frac{d^2x}{dt^2}\right|_{t=t_n}+\left.\frac{h^3}{3!}\frac{d^3x}{dt^3}\right|_{t=t_n}+\left.\frac{h^4}{4!}\frac{d^4x}{dt^4}\right|_{t=t_n}+…
\end{align}
\)
と書けます。
ここで、テイラー展開としてどの程度一致させて\(x(t_n+h)\)を決定するか？を表すのが次数に当たります。

言葉で書くなら、

局所的な精度は，高次項が解のテイラー(Taylor)展開とどの程度マッチしているかによって測定される．オイラー法は一次精度なので，誤差は一次高く\(h^2\)というベキ乗から始まる． ~NDSolveの”ExplicitRungeKutta”メソッドより

ともあります。

Butcher tableによるルンゲ=クッタ法の記述

行列形式で与えられるルンゲ=クッタ法での係数\(a_{i,j}, b_{i},c_{i}\)は何なのか？
具体的に記述してみましょう。
オイラー法(1段1次)はもっとも単純で、係数は
\(
\begin{align}
a_{1,1}&=0　\\
b_{1}&=1 \\
c_{1}&=0
\end{align}
\)
です。これを一般的な表記法の式に当てはめれば、
\(
\begin{align}
g_1&=x_n+h a_{1,1}k_1 \\
k_1&=f(t_n+c_1h, g_1) \\
x_{n+1}&=x_n+h b_1k_1
\end{align}
\)
となります。

中点法は、
\(
\begin{align}
a_{1,1}&=0 \\
a_{1,2}&=0 \\
a_{2,1}&=1/2 \\
a_{2,2}&=0 \\
b_{1}&=0 \\
b_{2}&=1 \\
c_{1}&=0 \\
c_{2}&=1/2
\end{align}
\)
という組で与えられます。

この係数行列の組はまとめてButcher tableと呼ばれる表記をするのが便利です。

これは、\(a_{i,j}, b_{i},c_{i}\)を
Buchertable
としてまとめて書く表記法です。

再び、オイラー法はButcher tableで書くと
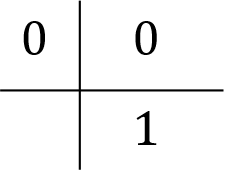
euler_butcher
とまとめて書くことができます。
中点法は
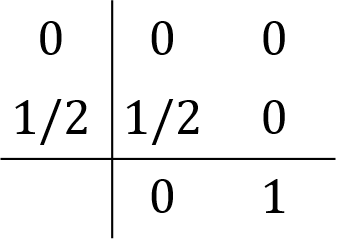
midpoint_butcher
RK4は
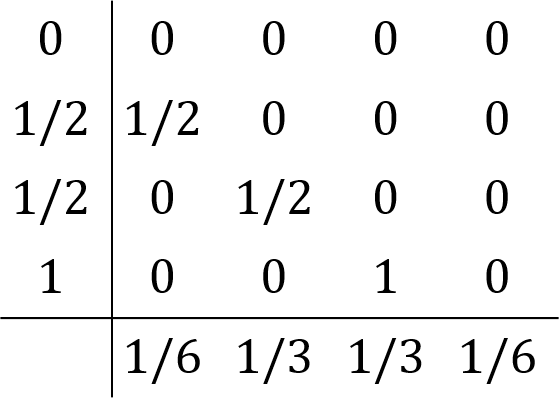
rk4_butcher
です。

高次のルンゲ=クッタ法(10,12,14次)

4次、5次…とずっとあるわけです。
こんなページがありました[3]。
High-Order Explicit Runge-Kutta Methods
この上のページには

  • 17段10次(8次が埋め込まれてる)
  • 25段12次(10次が埋め込まれてる)
  • 35段14次(12次が埋め込まれてる)

といったButcher tableにおける係数の値が書かれています。埋め込まれてる、の意味は次の節で説明します。
ただし、上のページのbutcher tableは
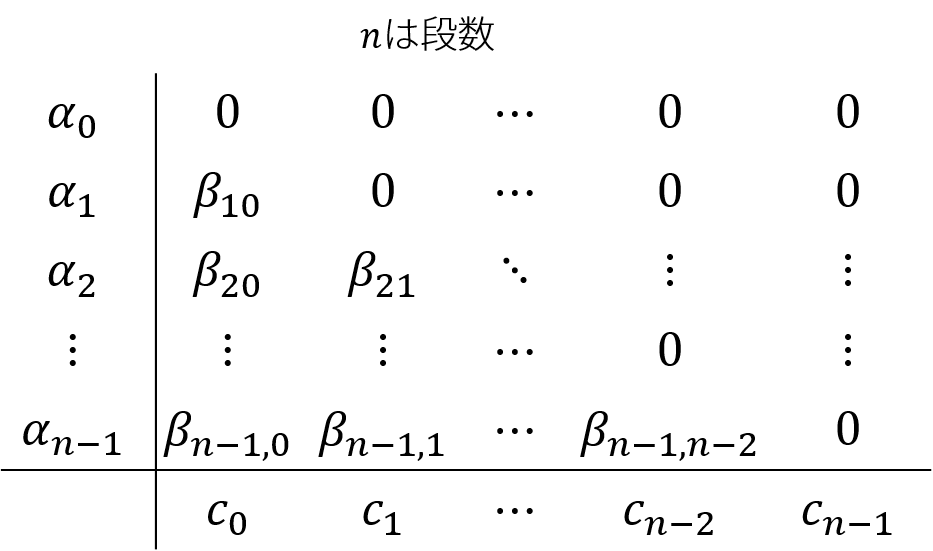
highorderbutcher2
となっているので注意が必要です。

埋め込まれた陽的ルンゲ=クッタ法

“埋め込まれた“という表現が出てきたのでその説明を行いましょう。
日本語では『埋め込まれた陽的ルンゲ=クッタ法』、英語では『embedded explicit runge-kutta method』と呼ばれるものがあります。
これは、p段q次陽的ルンゲ=クッタ法を作ったら、別の次数の陽的ルンゲ=クッタ法も、係数行列\(a_{i,j}, c_{i}\)を使って作れるじゃありませんか!
というものです。

Butcher tableは、この場合extended Butcher tableと呼ばれ、こういう形式で書かれます。
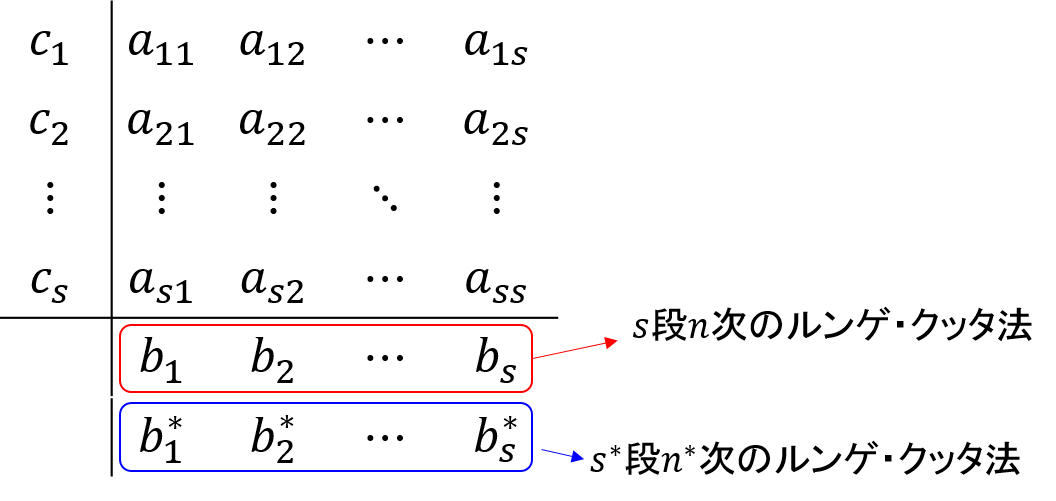
embedded_rk
この埋め込まれたルンゲ=クッタ法のいいところは、

  1. 計算誤差の評価ができる
  2. 刻み幅を自動的に制御できる、適応刻み幅制御。(応用として。)

という点です。ルンゲ=クッタ法によって得られた解が真の解とどのくらい違っているのか？が評価できるんです。

例えば、4次のルンゲ=クッタ法を使って得られた解\(x^{(4)}(t)\)と5次のルンゲ=クッタ法を使って得られた解\(x^{(5)}(t)\)があったとします。
もしも、\(x^{(4)}(t)\)と解\(x^{(5)}(t)\)の解の差を調べ、その差が無かったらその数値計算解は真の解に限りなく近い、と判断することができ、差が大きかったらその解は真の解から離れていて、数値計算の精度が足らない、と判断することができます。どちらも1つだけの解では出来なかったことです。

精度が足らない場合、刻み幅を小さくすれば精度が上がります。また逆に、精度が十分に足りている場合、刻み幅を大きくし、計算時間を減らすことができます。
これが適応刻み幅制御なのです。

違った次数のルンゲ=クッタ法を、まるで別々に計算してもいいのですが、そうすると計算時間が単純に考えておおよそ2倍になります。
解を評価するために2倍の計算時間が必要というのは良くない計算効率です。
そこで考えられたのが埋め込まれたルンゲ=クッタ法なのです。

具体例を挙げましょう。
一番簡単な埋め込まれたルンゲ=クッタ法は、ホイン法と呼ばれています。
butcher_heun
1行目は2次のオーダーを持ち、2行目は1次のオーダーを持ちます。

また、4次と5次を持つ埋め込まれたルンゲ=クッタ法は、ルンゲ=クッタ=フェールベルグ(Runge-Kutta-Fehlberg)法と呼ばれています。
その埋め込まれたルンゲ=クッタ法は、
butcher_rkf45
と書かれます。1行目は5次のオーダー、2行目は4次のオーダーを持ちます。

ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(適応刻み幅制御)

さて、次数の違う2つのルンゲ=クッタ法を用いて、適応刻み幅制御を行いたいと考えます。
刻み幅を制御するにあたって、適当に精度良かったから2倍にしてもまだ大丈夫だろ、とか差が大きすぎるから刻み幅半分にしよう、ということをやってはいけません。
適当にやったら計算時間が余計にかかり、精度が良くない変な結果が得られます。

[5~9]によれば、ルンゲ=クッタ=フェールベルグ法において区間\(i\)での最適な刻み幅\(h’\)は区間\(i\)の誤差評価の結果を使って、
\(
\displaystyle h’=\delta h=\left(\frac{\varepsilon h}{2|x^{(5)}_{i}-x^{(4)}_{i}|}\right)^{1/4} h
\)
と予想できます。ここで\(\varepsilon\)はエラーを制御する精度の目安で、おおよそ計算時に要求する相対誤差です。もちろん、この\(h’\)は区間\(i\)の最適な幅ですが、関数に劇的な変化は無いだろうとして、次の区間の計算の一番初めに用いる刻み幅を推定するのです。
なので、\(i+1\)番目の計算区間では、計算するときはこの\(h’\)の値を使えばいいんです。
(ちなみに、m次ルンゲ=クッタ法の場合では
\(
\displaystyle h’=\delta h=\left(\frac{\varepsilon h}{2|x^{(m+1)}_{i}-x^{(m)}_{i}|}\right)^{1/m} h
\)
と推測されます。)

詳しい理由は分かりませんが、5次オーダーではなく、4次です。5次のオーダーは誤差評価のためだけに用いられているようです。
ルンゲ=クッタ=フェールベルグ法の計算スキームは[7]に詳しく書かれています。
日本語訳して、その計算スキームを書けば下のようになります。


ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(プログラム)

講義のレポート等の宿題で使うのは僕の意向と異なるので使用はご控えください。
研究目的、趣味、確かめの場合はミスがあるかもしれないことを念頭に置いたうえならば使用と改変をご自由にしてください。
このプログラムを使用して生じた責任は取りません。

fortran90によるプログラムです。ほぼ上の説明をそのままプログラミングしたものです。

  • 実数、1階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d}{dx}y=y\cos x,~~y(x=0)=1
    \)
    を倍精度実数、刻み幅制御で\(x=10\)まで解く事を考えます。
    解析解は
    \(
    \displaystyle y(x)=exp(sin(x))
    \)
    です。コードは以下の通りです。

  • 実数、2階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d^2}{dx^2}y=-\frac{1}{4}y,~~y(x=0)=1,~ y'(x=0)=0
    \)
    を倍精度実数、刻み幅制御で\(x=20\)まで解く事を考えます。コードは以下の通りです。

    ※ここで使われているサブルーチンdrkf45は実数一階微分のプログラム内にあるルーチンと一字一句同一です。

  • 複素数、1階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d}{dx}y=y\cos x,~~ y(x=0)=1+i\frac{1}{2}
    \)
    を倍精度実数、刻み幅制御で\(x=10\)まで解く事を考えます。コードは以下の通りです。

  • 複素数、2階微分方程式

    • 微分方程式
    \(
    \displaystyle \frac{d^2}{dx^2}y=-\frac{1}{4}y,~~ y(x=0)=1+i\frac{1}{2},~y'(x=0)=0+i0
    \)
    を倍精度実数、刻み幅制御で\(x=20\)まで解く事を考えます。コードは以下の通りです。

    ※ここで使われているサブルーチンcrkf45は複素数一階微分のプログラム内にあるルーチンと一字一句同一です。

等間隔の出力の場合は、以下の通りで実行できます。
サブルーチンはdrkf45は変わっていません。

[adsense2]

不連続な点を含む場合

不連続な点を含む場合、境界条件を指定しないと解くことはできません。

さて、ここで微分方程式
\(
\begin{eqnarray}
\frac{dy}{dx}=
\left\{
\begin{aligned}
0\;\;(x\le 0)\\
1\;\;(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
を初期条件\(y(-0.095)=0\)の下で考えます(意図的に境界条件は考えません)。
これを4次ルンゲ=クッタと適応刻み幅ルンゲ=クッタで解いてみましょう。
プログラム上ではそのまま解くことが出来ます。
実際に解かせてみますと、
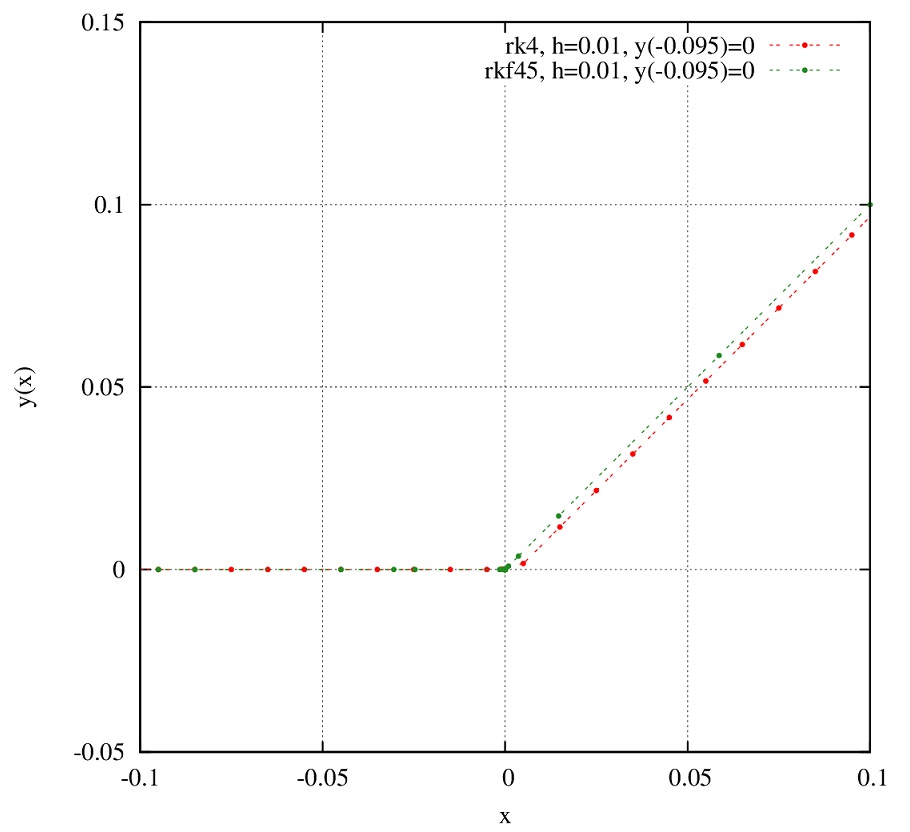
rk4_rkf451_disc
となり、2つの結果(赤：4次ルンゲ=クッタ、緑：刻み幅制御ルンゲ=クッタ)は異なってしまいます。これは1階微分の不連続性のため発生します。
不連続点\(x=0\)で関数\(y(x)\)に境界条件を指定しない限り、どちらも正しい解なのです。

さて、なぜこんなことが発生するのでしょうか？以下のように問題を表すことにします。

不連続な点を含む1階の微分方程式を考えます。
ここで不連続、という意味は関数\(y(x)\)の一階微分が、点\(x’\)で
\(
\displaystyle \left. \frac{dy}{dx}\right|^{x=x’+0}_{x=x’-0}=a,\;\;\;(a\ne 0)
\)
であるような点を指しているとします。

上記の例題を考えてみましょう。
上記の例題では\(a=1\)です。微分方程式を解析的に解いてみますと、
\(
\begin{eqnarray}
y(x)=
\left\{
\begin{aligned}
C_0\;\;(x\le 0)\\
x+C_1\;\;(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。ここで\(C_0, C_1\)は定数です。
\(C_0, C_1\)は\(y(x)\)が解きたい問題の境界条件によって決まります。

例えば、\(y(x)\)は全領域に対して繋がっている、という条件を課しましょう。この場合、不連続点\(x’\)で
\(
\displaystyle \left. y(x)\right|^{x=x’+0}_{x=x’-0}=0
\)
という境界条件を満たさなければなりません。この条件を課すと、\(C_1=C_0\)となり、初めて関数\(y(x)\)を一意に決めることが出来ます。

1階微分方程式を解く場合、適応刻み幅制御では関数\(y(x)\)は計算領域内で繋がっている事が課されています。しかし、4次ルンゲ=クッタではその条件は課されません。\(C_1\)の値は初期条件に依存し、一意に関数が決まりません。
どちらが悪いという話ではありません。

通常は適応刻み幅でも、4次ルンゲ=クッタでも\(y(x)\)にどこか連続ではない変な点がある場合、その点で区間を別々に分けて解きます。その後、境界条件に従って値を調節して全体の関数を構成します。

ベンチマーク用

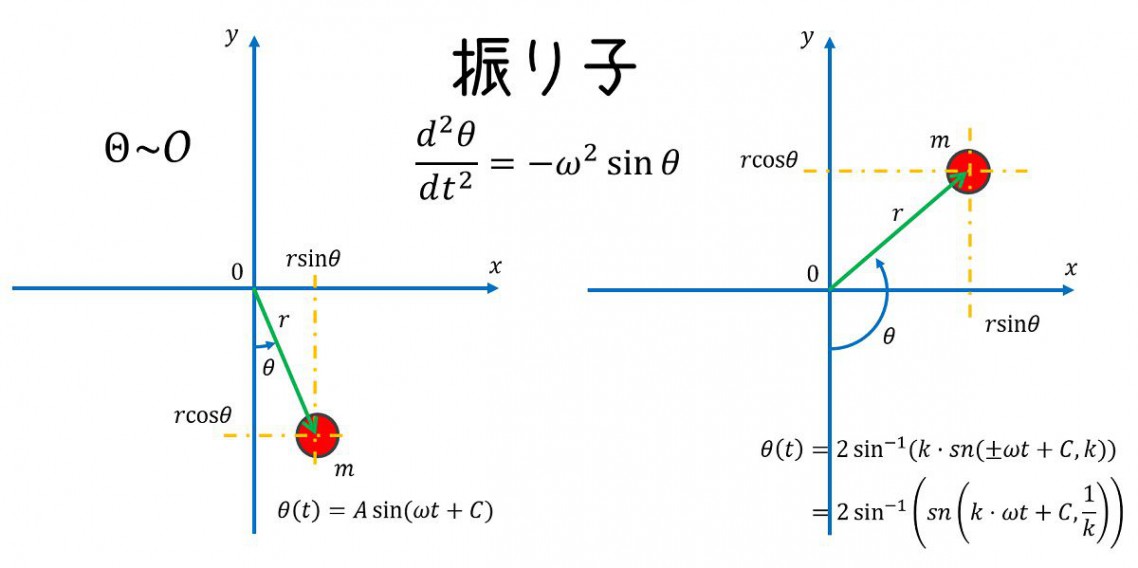
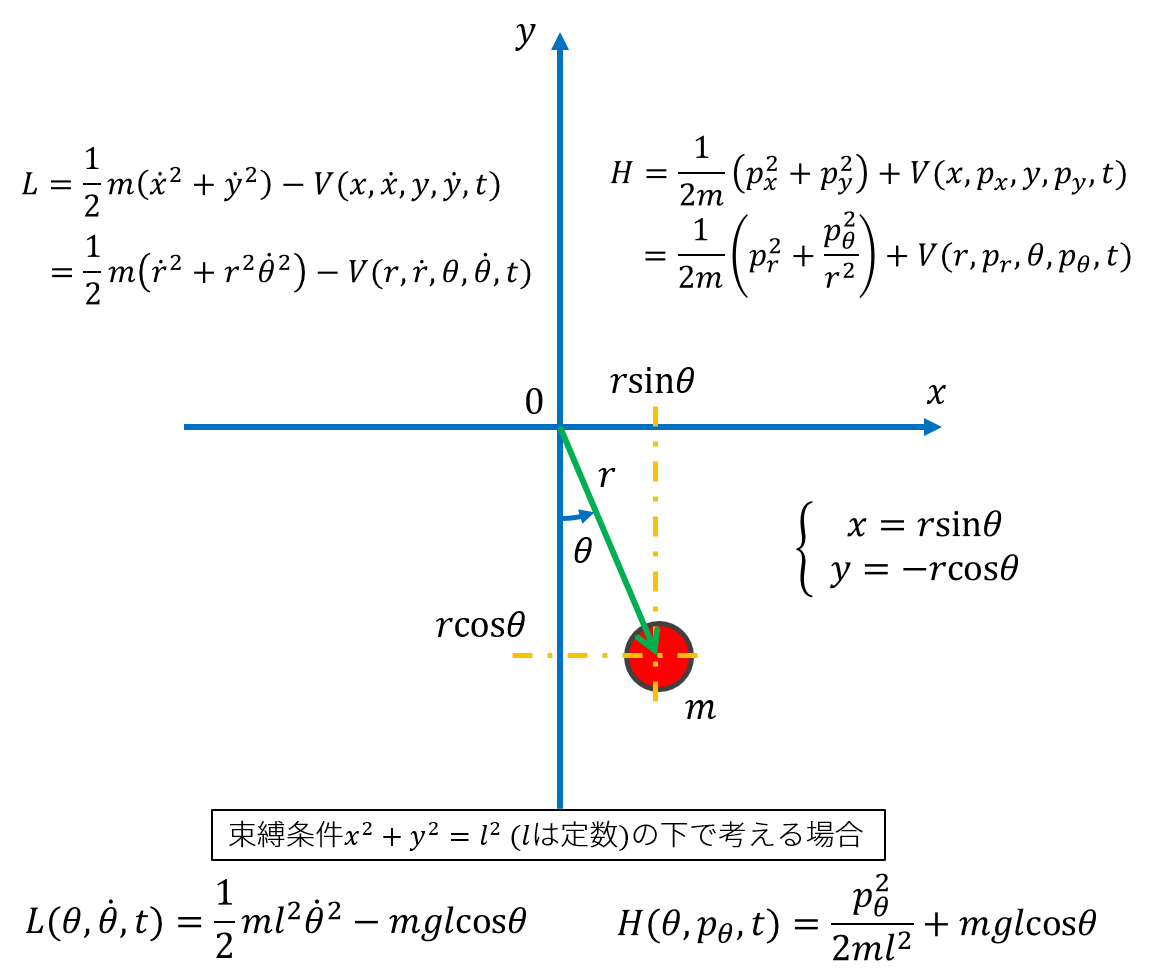
微分方程式の解法がどれくらい正しそうかのベンチマーク問題として振り子(角度が大きい時)を考えましょう(振り子の詳しい解説はこちら)。
以下の\(\omega=1\)としたときの運動方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\sin\theta
\)
を
\(
t=0,\; \theta=0; \frac{d\theta}{dt}=1.9\cdots (k=0.95)
\)
の初期条件の下解いた場合、
1周期\(T\)は
\(
T=4K(0.95)=10.360044923498004876778\cdots
\)
となります。
この値はwolfram alphaから求めました。
4EllipticK[0.950.95] wolfram alpha

刻み幅制御を行い、45000周期目の値を考えます。45000周期目は時刻
\(
T_{45000}=466202.0215574102\cdots
\)
です。刻み幅制御による精度を\(10^{-12}\)に設定し、数値計算を行わせます。

すると実行結果として”fort.10″に

0.4662020113E+006  -0.2103356901E-001   0.1899883579E+001   0.4224109363E-002
0.4662020155E+006  -0.1300808922E-001   0.1899955473E+001   0.4223843994E-002
0.4662020198E+006  -0.4982881533E-002   0.1899993468E+001   0.4223658015E-002
0.4662020240E+006   0.3042061693E-002   0.1899997567E+001   0.4223520921E-002

というデータが出力されます。
1列目が時刻\(t\)、2列目が\(\theta(t)\),3列目が\(\frac{d\theta(t)}{dt}\),4列目が刻み幅\(h\)です。
1回のステップでの要求精度12桁に対し、最終的な結果は8桁まで正しい値を出しています。
この時、計算回数は77,852,488回\(~10^{8}\)回行われているので、最終的な結果として4桁は少なくとも正しいと考えられます。
4桁合っていればいい状況で8桁もあっているのは、被積分関数が変な振る舞いをしないからでしょう。

また、60000周期で確認してみると(\(T_{60000}=621602.695409880292\cdots\))

0.6216026888E+006  -0.1531918479E-001   0.1899938246E+001   0.4223959920E-002
0.6216026930E+006  -0.7293808996E-002   0.1899986003E+001   0.4223717084E-002
0.6216026973E+006   0.7312355417E-003   0.1899999862E+001   0.4223582630E-002
0.6216027015E+006   0.8756011575E-002   0.1899979827E+001   0.4223462029E-002

です。
1回のステップでの要求精度12桁に対し、最終的な結果は8桁まで正しい値を出しています。
この時、計算回数は103,803,513回\(~10^{8}\)回行われているので、最終的な結果として4桁は少なくとも正しいと考えられます。
･･･まだまだ大丈夫そうですね。

少し特殊な初期条件(\(k=1\))でやってみましょう。
この\(k=1\)は、振り子の質点がちょうど真上に来て静止する非常に不安定な状態です。
何秒間静止していられるか試してみましょう。刻み幅の制御等は上記条件と同じです。
横軸に時間\(t\)、縦軸に\(\theta(t)\)を取った時のグラフです。
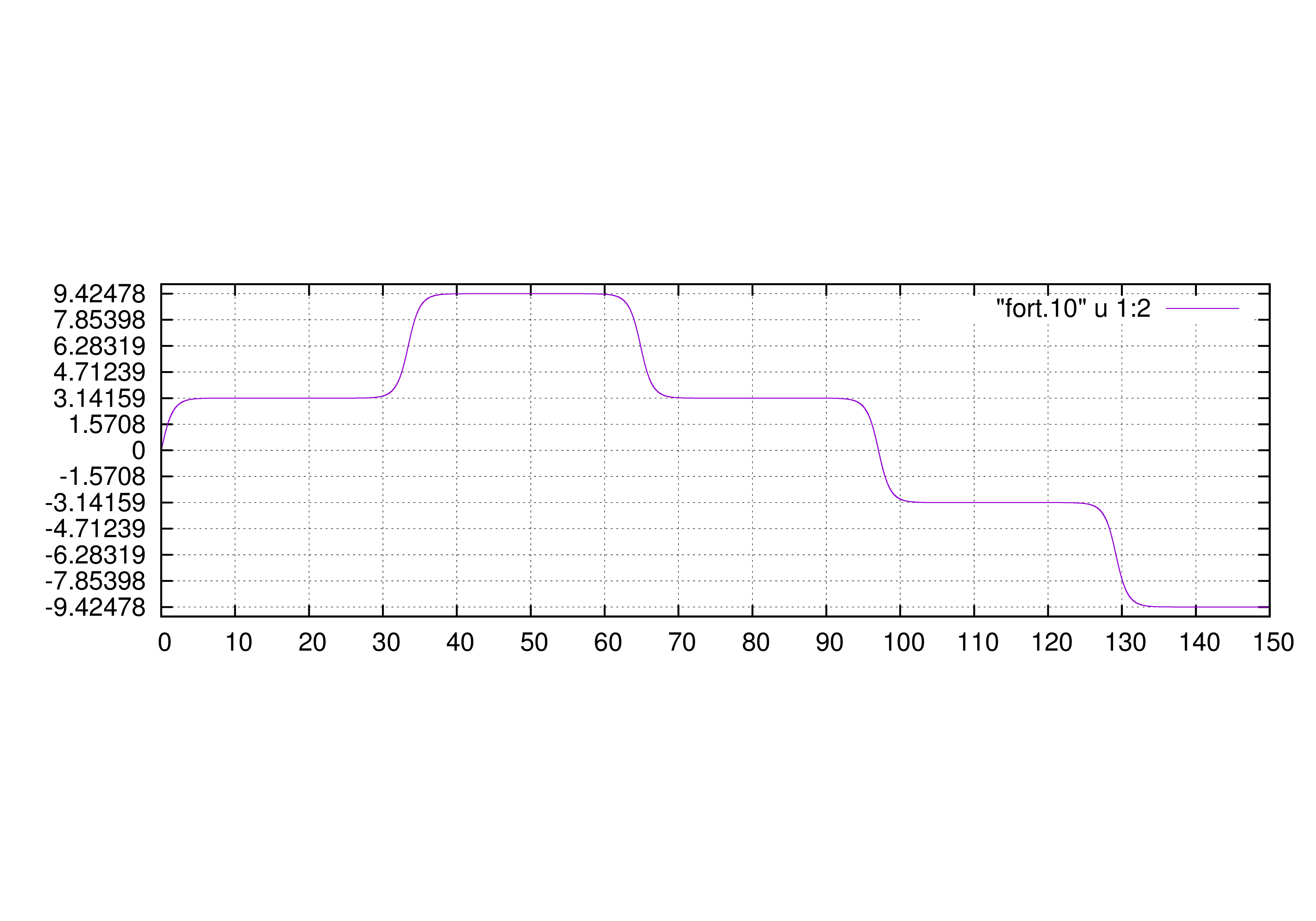
ellk1
すぐに破綻しました。正しい値は\(t=20\)位までですかね。これは、機械的な誤差があることによって不安定な平衡点からほんの少しだけ外れてしまったからです。だからカオスとかを考えるときとかは注意しなければなりません。

ルンゲ=クッタ=ドルマンド=プリンス法

フェールベルグ法は初期の頃に考えられた埋め込まれた方法です。
研究が進み、実用上では別の係数の組み合わせが良いことが分かってきました。
その一つが1980年に発見されたドルマンド=プリンス(Dormand-Prince)法です。

これは、7段4(5)次の方法です。
フェールベルグ法は6段4(5)次の方法ですので、次数は同じです。

良く調べていませんが、この違いは、4次の結果を基準にして求めたブッチャー係数(フェールベルグ法)か、5次の結果を基準に求めたブッチャー係数(ドルマンド=プリンス法)か？の違いのようです。

単純に考えて、同じ次数なのにドルマンド=プリンス法の方が段数が増えていて効率が悪いです。
しかし、本来は7段なのですが、7段目に呼び出した結果を取って置けば、次のステップの1段目に同じ値が使えるように設計されているので、プログラム上は6段と(ほぼ)同じ関数の呼び出し回数になります。

プログラムはこんな感じになるでしょう。

適当な刻み幅で出力

等間隔(サブルーチンは上のものと同じなので省略)

program main
  implicit none
  integer::i,N,info,Nx
  double precision::h,tol
  double precision::xa,xb,tx
  double precision,allocatable::y(:),x(:),work0(:)
  double precision,external::grk

N=1
  allocate(y(1:N),work0(1:N))

Nx=101
  allocate(x(1:Nx))
  xa=0d0
  xb=10d0
  do i=1,Nx
     x(i)=(i-1)*(xb-xa)/dble(Nx-1)+xa
  enddo

!initial conditions
  y(1)=1d0  ! x (0)

tol=1d-8
  write(10,'(2e25.10e3)')x(1),y(1)
  do i=2,Nx
     info=-1
     h=x(i)-x(i-1)
     tx=x(i-1)
     do while(info.le.0)
        call dDP45(grk,tx,h,N,y,x(i),info,tol,work0)
     enddo
     write(10,'(2e25.10e3)')x(i),y(1)
  enddo

stop
end program main

function grk(N,x,y,s)
  implicit none
  integer,intent(in)::N,s
  double precision,intent(in)::x
  double precision,intent(in)::y(1:N)
  double precision::grk

grk=0d0
  if(s.eq.1)then
     grk=y(1)<em>cos(x)
  else
     write(6,</em>)"***Error grk"; stop
  endif

return
end function grk

4倍精度ルーチン

4倍精度のサブルーチンです。
計算速度は倍精度の30~50倍かかるので、必要なとき以外使わないようにしましょう。

陽的ルンゲ=クッタ法の導出

ルンゲ=クッタ法の導出は煩雑です。単に複雑なだけです。
導出過程について詳しく述べられているページは、早川様が記述された以下のpdfを参照すると良いと思います。
Runge-Kutta法についてのノート(早川尚男)
計算過程を含め記述されているので分かりやすいです。

参考文献

[1]Derivation of Runge–Kutta methods
[2]NDSolveの”ExplicitRungeKutta”メソッド
[3]High-Order Explicit Runge-Kutta Methods
[4]List of Runge–Kutta methods
[5]Runge-Kutta-Fehlberg Method (RKF45)
[6]Runge-Kutta-Fehlberg method
[7]Lecture:13Runge-Kutta-Fehlberg Method
[8]GPU acceleration of Runge Kutta-Fehlberg and its comparison with Dormand-Prince method
[9]William H. Pressら著『ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ– 』(1993)

ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ

↑この本が一番有益だと思います。Fortran版もありますが、英語しかありません。ちなみに、英語で,若干古いバージョンでいいのならば
公式のホームページ
Numerical Recipes in C (1992)
Numerical Recipes in Fortran 77 and Fortran 90 (1992, 1996)
で無料で公開されています。

物理学

運動量演算子の導出

コメントする

量子力学の運動量演算子\(\hat{p}\)が
\(
\displaystyle \hat{p}=-i\hbar \frac{d}{d x}
\)
であらわされることを導出します。
ここでの”導出”は運動量演算子として妥当なものを導出する、と言った方がいいかもしれません。

平行移動演算子\(\hat{T}\)を出発点とします。
この平行移動演算子はある波動関数\(\psi_{(x)}\)を平行移動させる演算子で、これを作用させると
\(
\hat{T}_{(\Delta x)}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
となる演算子です。

よく説明される、シュレディンガー方程式の平面波解からの出発はしません。

この\(\hat{T}\)の持つであろう性質を考え、その特性から\(\hat{T}\)の具体的な形を推定し、運動量演算子を導きます。

平行移動演算子\(\hat{T}\)が満たすべき性質

当たり前と思われる性質から、平行移動演算子に関して以下の4つが言えます。

  1. 波動関数\(\psi_{(x)}\)が1に規格化済みであれば、平行移動した波動関数\(\psi_{(x+\Delta x)}\)もまた規格化されているはずである。
    すなわち、
    \(
    \begin{align}
    \langle\psi_{(x)}|\psi_{(x)}\rangle &= \langle\psi_{(x)}|\hat{T}^{\dagger}_{(\Delta x)}\hat{T}_{(\Delta x)}|\psi_{(x)}\rangle \\
    &= \langle\psi_{(x+\Delta x)}|\psi_{(x+\Delta x)}\rangle \\
    &\rightarrow \hat{T}^{\dagger}_{(\Delta x)}\hat{T}_{(\Delta x)}=\mathbf{1}
    \end{align}
    \)
    となり、3本目の式から\(\hat{T}\)はユニタリー演算子であることがわかります。
  2. \(\Delta x\)進めた後、\(\Delta x^{\prime}\)を進める操作は\(\Delta x + \Delta x^{\prime}\)進める操作に等しいはずである。
    すなわち、
    \(
    \hat{T}_{(\Delta x^{\prime})}\hat{T}_{(\Delta x)}=\hat{T}_{(\Delta x+\Delta x^{\prime})}
    \)
  3. 負の方向への平行移動\(\hat{T}_{(-\Delta x)}\)は正の方向への平行移動\(\hat{T}_{(\Delta x)}\)の逆のはずである。
    \(
    \hat{T}_{(-\Delta x)}=\hat{T}^{-1}_{(\Delta x)}
    \)
  4. \(\Delta x\)が0のとき、恒等操作なはずである。
    \(
    \begin{align}
    \hat{T}_{(0)}\psi_{(x)}&=\psi_{(x)} \\
    &\rightarrow \hat{T}_{(0)}=\mathbf{1}
    \end{align}
    \)

平行移動演算子の具体的な形

1,より、\(\hat{T}_{(\Delta x)}\)はユニタリー演算子である事が分かりました。ユニタリー演算子を作る1つの方法として、エルミート演算子\(\hat{A}_{(\Delta x)}\)を用いて、
\(
\hat{T}_{(\Delta x)}=e^{i\hat{A}_{(\Delta x)}}
\)
と置けば、\(\hat{T}_{(\Delta x)}\)はユニタリー演算子となります(エルミート演算子とユニタリー演算子の性質)。
この仮定の下、
\(
\hat{T}_{(\Delta x)}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
に代入して、
\(
e^{i\hat{A}_{(\Delta x)}}\psi_{(x)}=\psi_{(x+\Delta x)}
\)
無限小移動を考えて\(\Delta_{(x)}\rightarrow 0\)と約束すれば、
\(
(1+i\hat{A}_{(\Delta x)})\psi_{(x)}=\psi_{(x+\Delta x)}
\)
変形して、
\(
\psi_{(x+\Delta x)}-\psi_{(x)}=i\hat{A}_{(\Delta x)}\psi_{(x)}
\)
辺々を\(\Delta x\)で割れば、
\(
\begin{align}
\displaystyle \lim_{\Delta x\rightarrow 0}\frac{\psi_{(x+\Delta x)}-\psi_{(x)}}{\Delta x} = \lim_{\Delta x\rightarrow 0} i\frac{\hat{A}_{(\Delta x)}}{\Delta x}\psi_{(x)}
\end{align}…(i)
\)
となります。左辺は位置\(x\)における波動関数の傾きです。
ここで右辺を見ます。\(\hat{A}_{(\Delta x)}\)は\(\Delta x\)のなんらかの関数であるはずですが、\(\hat{A}_{(\Delta x)}\)が分母の\(\Delta x\)と打ち消す形でなければ0、もしくは発散する事になります。
この場合、波動関数の傾きが到る点で0になるということは、全空間で定数ということになり非物理的な解です。また、発散してしまうのであれば波動関数が至る所で発散してしまい、これまた日物理的です。

具体的に、もしも\(\hat{A}_{(\Delta x)}=(\Delta x)^2\)だったら、
\(
\displaystyle \lim_{\Delta x\rightarrow 0} \frac{(\Delta x)^2}{\Delta x}=\lim_{\Delta x\rightarrow 0} \Delta x =0
\)
であるし、もしも\(\hat{A}_{(\Delta x)}=(\Delta x)^{1/2}\)だったら
\(
\displaystyle \lim_{\Delta x\rightarrow 0} \frac{(\Delta x)^{1/2}}{\Delta x}=\lim_{\Delta x\rightarrow 0} \frac{1}{\sqrt{\Delta x}} =\infty
\)
となります。
すなわち、言いたいことは、\(\hat{A}_{(\Delta x)}\)は\(\Delta x\)に関して1次であるべきで、
\(
\hat{A}_{(\Delta x)}=\hat{B}\cdot \Delta x
\)…(ii)
と書けるはずです。ここで\(\hat{B}\)は\(\Delta x\)に依らない演算子です(下に補足説明あり)。

よって、式(i)は\(\Delta x\rightarrow 0\)のとき、
\(
\begin{align}
\displaystyle \lim_{\Delta x\rightarrow 0}\frac{\psi_{(x+\Delta x)}-\psi_{(x)}}{\Delta x} &= \lim_{\Delta x\rightarrow 0} i\frac{\hat{A}_{(\Delta x)}}{\Delta x}\psi_{(x)} \\
\frac{d \psi_{(x)}}{dx}=i\hat{B}\psi_{(x)}
\end{align}…(iii)
\)
と書けるため、
\(
\psi_{(x)}=e^{i\hat{B}\cdot x}\psi_{(0)}
\)
となります。(この式で右辺の\(\psi_{(0)}\)が0である必要はなく、定数であればいいんです。)

平行移動演算子と運動量演算子との関係

次元について考えましょう！
今、\(\hat{T}_{(\Delta x)}=e^{i\hat{B}\cdot \Delta x}\)であり、\(\Delta x\)の次元は\(\mathrm{[m]}\)であるため、\(\hat{B}\)の次元は\(\mathrm{[m^{-1}]}\)でなければなりません。よって、\(\hat{B}\)は波数の次元を持つ演算子であると考えられるため、\(\hat{B}\)を\(c\hat{k}\)と記述することにします。ここで、\(c\)は無次元の定数です。
式(iii)より、
\(
\displaystyle \frac{d \psi_{(x)}}{dx}=ic\hat{k}\psi_{(x)}
\)
辺々に\(-i\hbar\)を掛けると、
\(
\displaystyle -i\hbar \frac{d}{dx} \psi_{(x)}=c\hbar \hat{k}\psi_{(x)}
\)…(iv)

!!!

\(p=\hbar k\)は運動量を表すものでした。よって,\(\hat{p}=\hbar \hat{k}\)と書けば、式(iv)より
\(
\begin{align}
\hat{p}\psi_{(x)}&=\frac{1}{c}\left[-i\hbar\frac{d}{d x}\right] \psi_{(x)} \\
\end{align}
\)
となります。よって運動量演算子は
\(
\begin{align}
\hat{p}\propto -i\hbar\frac{d}{d x} \\
\end{align}
\)
となります。この考えからは定数倍を含めてしまうので、比例する、という事しか言えません。

なぜ決まらないのか考えてみますと、時間の依存性に関する考え方が式のどこにも含んでいないからです。
時間の単位が決まらないと速度の定義が出来ないわけで、これ以上進めることが出来ないのです。

各成分について言えるので、多次元の場合では
\(
\hat{p}_x\propto -i\hbar\frac{\partial}{\partial x}
\)
としても同じことです。
申し訳ないですが、数学的に厳密か？は保証しません。

補足説明

果たして運動量演算子として考えた\(e^{i\hat{B}\cdot \Delta x}\)は\(\hat{T}\)の特性1.~4.を満たすでしょうか？

  1. \(
    \left(e^{i\hat{B}\cdot \Delta x}\right)^{\dagger} \left(e^{i\hat{B}\cdot \Delta x}\right)=e^{-i\hat{B}^{\dagger}\cdot \Delta x}e^{i\hat{B}\cdot \Delta x}=\mathbf{1}
    \)
    ここで\(\hat{B}\)はエルミート演算子を考えているので、\(\hat{B}^{\dagger}=\hat{B}\)です。
    \(
    e^{-i\hat{B}^{\dagger}\cdot \Delta x}e^{i\hat{B}\cdot \Delta x}=\mathbf{1}
    \)
    ok!
  2. \(
    \hat{T}_{(\Delta x^{\prime})}\hat{T}_{(\Delta x)}=\hat{T}_{(\Delta x+\Delta x^{\prime})}
    \)    か？
    \(
    (\mbox{左辺})=e^{i\hat{B}\cdot \Delta x^{\prime}} e^{i\hat{B}\cdot \Delta x}=e^{i\hat{B}\cdot (\Delta x^{\prime}+\Delta x)}
    \)
    ok!
  3. \(
    \hat{T}_{(-\Delta x)}=\hat{T}^{-1}_{(\Delta x)}
    \)    か？
    両辺の左から\(\hat{T}_(\Delta x)\)を掛けて、
    \(
    \begin{align}
    &\hat{T}_{(\Delta x)}\hat{T}_{(-\Delta x)}=\mathbf{1} \\
    &= e^{i\hat{B}\cdot \Delta x}e^{i\hat{B}\cdot (-\Delta x)}=e^{i\hat{B}\cdot 0}=\mathbf{1}
    \end{align}
    \)
    ok!
  4. \(e^{i\hat{B}\cdot 0}=1\)
    ok!

よって、4つすべてを満たすので、\(\hat{T}_{(\Delta x)}=e^{i\hat{B}\cdot \Delta x}\)は平行移動演算子として適当であると考えることができるのです。

プログラミングと数値計算

数値積分(等間隔)

コメントする

数値計算での積分方法、特に等間隔の分点の場合であるニュートン・コーツ積分(とロンバーグ積分)に関する理論とのプログラムを載せます。

  1. ニュートンコーツ型の公式
  2. ルンゲ現象
  3. ロンバーグ積分
  4. サブルーチン”integral”のコードと使い方
  5. サブルーチン”romberg”のコードと使い方

等間隔の分点で積分を行う場合、よく使われる方法は台形則、もしくはシンプソン積分です。

台形則

台形則は、分点間を台形近似して面積を求める方法であり、下図のようなイメージで積分を近似する方法です。
外形_台形_c
積分\(\displaystyle \int_a^b f(x) dx\)を、
\(
\displaystyle \int_a^b f(x) dx \sim \sum_{i=0}^{N-1} \frac{f(x_{i+1})+f(x_i)}{2}h
\)
として近似します。この時、誤差のオーダーは\(O(h^3)\)となります。
言い換えると、
台形積分とは、隣り合う分点間を1次関数で近似して求める積分
言えます。

シンプソン積分

シンプソン積分は、隣り合う分点間を2次関数で近似して求める積分です。イメージは
外形_シンプソン_c
な感じです。数式では
\(
\displaystyle \int_a^b f(x) dx \sim \sum_{i=0}^{N/2} \frac{f(x_{2i})+4f(x_{2i+1})+f(x_{2i+2})}{3}h
\)
となります。

高次≠高精度

これ以降もあります。分点間を3次、4次、…としていけば高次の積分をすることが可能になります。
この分点間の次数をどんどん上げていって積分をする方法をまとめてニュートンコーツの公式、と呼びます。
例えばの台形則はニュートンコーツの公式の1次に相当し、シンプソン則はニュートンコーツの公式の2次に相当しています。

じゃあ100次の公式作れば精度が凄い公式ができるんじゃないか？となりますが、これは違います。
高次であることと精度が高いことは違うのです。だから使うな、というわけではなくて知っておいてほしいことなんです。
ではなぜか？これはwikipediaのニュートンコーツの公式のページからとってきたものですが、この式に理由があります。
ニュートンコーツ型式_c

問題となるのが誤差項です。例えば台形近似を見ますと、誤差項は\(h^3 f^{(2)}(\xi)\)とあります。hは刻み幅なので、この項は刻み幅を小さくすれば小さくするほど精度がよくなることを言っています。
が、問題は\(f^{(2)}(\xi)\)の方です。この項は本当の関数が分からないと評価できません。
多項式だったら微分するごとに次数が1つづつ減少するのでこの項は高次になれば小さくなります。じゃあもしも微分するごとに値が増加していったら…？この場合、hを小さくしてもそれを上回るくらい\(f^{(2)}(\xi)\)が大きくなることがあります。これをルンゲ現象と呼びます。

ルンゲ現象

例えば関数
\(
\displaystyle f(x)=\frac{1}{1+25x^2}
\)
を考えます。wikipediaのページを参考にすれば、その導関数と値は、
ルンゲ現象_c
となります。高次になればなるほど値が増加する関数なのです。
実際には\(h^n f^{(m)}(\xi)\)の積の値が小さいか大きいか？なので、一概には高次は悪い！とは言えません。高次は危ないくらいでしょう。

これを可能な限り回避するために、低次の積分を組み合わせて使う方法がとられます。
こうすることで高次の値を増加を抑えるのです。

そのほかの手法もいろいろあります。分点の位置に縛られなければガウス求積法が最高でしょう。素晴らしい方法です。ぜひ調べてみてください。

[adsense1]

ロンバーグ積分

さて、高次を追い求めるのもいいですが、一線を駕す…とまではいきませんが、ロンバーグ(Romberg)積分というものがあります。
このロンバーグ積分とは、台形則による計算を基本とし、無限小区間での積分結果を補外によって求めよう、というものです。
ここでいう補外の概念は以下のような感じです。

刻み幅1で台形則の結果から積分値S1が分かる
↓
刻み幅0.5で台形則による結果から積分値S2がわかる
↓
刻み幅0.25で台形則による結果から積分値S3がわかる
↓
刻み幅0.175で台形則による結果から積分値S4がわかる

とある程度計算していきます。そうすると刻み幅hを変化させるとそれに応じて積分値がS1→S2→S3→S4…と推移していくわけです。
この推移の仕方を計算すれば、刻み幅無限小の場合の積分値Sが分かる、こういう仕組みになっています。収束加速法と言ったり、リチャードソン補外、なんて言ったりします。
この補外による方法はかなり優れています。先ほどの高次がどうこう、といった問題が発生しないのです。台形則しか使ってないんですから。有限桁計算に適した方法である、とかwikipediaに載ってたりします。

ロンバーグ積分の詳しい計算方法や理論は
ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ

ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ

を見ると詳しく書かれています。

日本語では第6章 数値積分と数値微分にロンバーグ積分の記述があります。
英語ではRomberg integralで調べると良いでしょう。参考までに、英語では
Romberg integration exampleや、Romberg Integrationなにかがいいと思います。

2016/03/01
上のRomberg Integrationを参考にして書いたプログラムはこちらです。これは、解析関数fをRomberg積分するプログラムです。
解析関数ではなく、サイズ\(2^{n}+1\)の配列に格納されている場合はこのページの下の方にあるプログラムを参照してください。

call romberg(a,b,s,pre)

で呼び出し、区間a~bの積分\(s=\int_a^b f(x) dx\)を精度preで求めるプログラムです。

サブルーチン”integral”のコードと使い方

下のサブルーチン”integral”は1,2,3次元の短冊近似、台形則、シンプソン積分、シンプソン3/8積分、ブール則(ニュートン・コーツ型積分)をカバーします。
ただし、分点の個数に注意してください。分点の個数を気にせず使える近似方法は、短冊近似、台形近似のみです。

ロンバーグ積分では引数の関係上、ニュートン・コーツ型積分との間をうまく処理できなかったため、別のサブルーチンとして書きます。もしもロンバーグ積分を使いたい場合はもう少し先に進んでください。

まずはニュートン・コーツ型積分です。
下のサブルーチンを使ってください。
使い方は、

 call integral(配列の大きさ,配列,刻み幅,積分結果,積分手法)

という感じです。
実際のプログラムでは、以下のように使用してください。配列yは複素数解列(ただし実軸上の積分)でもokです。

1次元

サブルーチンintegralの使い方
積分則 呼び方
短冊近似(長方形近似)
 call integral(size(w,1),w,h,s,"box")
 配列yの大きさに指定はない。
台形近似
 call integral(size(y,1),y,h,s,"trapezoid")
 配列yの大きさに指定はない。
シンプソン則
 call integral(size(y,1),y,h,s,"simpson")
 配列yの大きさが3,5,7,…個、\(2n+1\)個でないといけない
シンプソン3/8則
 call integral(size(y,1),y,h,s,"simpson38")
 配列yの大きさが4,7,10,…個、\(3n+1\)個でないといけない
ブール則
 call integral(size(y,1),y,h,s,"boole")
 配列yの大きさが5,9,13,…個、\(4n+1\)個でないといけない

2次元配列の場合は以下のように指定してください。

 call integral(size(w,1),size(w,2),w,hx,hy,s,"simpson")

3次元の場合はこう指定してください。

 call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"simpson")

積分のためのモジュール

module integral_mod
  !developer --> sikino
  !date --> 2015/04/07
  implicit none
  interface integral
     module procedure &
          dintegral, &
          dintegral2d, &
          dintegral3d, &
          cintegral, &
          cintegral2d, &
          cintegral3d
  end interface integral
contains
  subroutine dintegral(N,y,h,s,method)
    integer,intent(in)::N
    double precision,intent(in)::h,y(1:N)
    character(*),intent(in)::method
    double precision,intent(out)::s
    integer::i
    double precision::y0,y1,y2,y3
       
    s=0.d0; y0=0.d0; y1=0.d0; y2=0.d0; y3=0.d0
   
    if(trim(method).eq."box")then
       s=h*sum(y(1:N-1))
    elseif(trim(method).eq."trapezoid")then
       y1=y(1)+y(N)
       do i=2,N-1
          y2=y2+y(i)
       enddo
       s=(y1+2.d0*y2)*h*0.5d0
    elseif(trim(method).eq."simpson")then
       if(mod(N,2).ne.1)then
          write(6,*)"=====cannot calculation with simpson"
          write(6,*)"=====program stop"
          stop
       endif

       y1=y(1)+y(N)
       do i=2,N-1,2
          y2=y2+y(i)
       enddo
       do i=3,N-2,2
          y3=y3+y(i)
       enddo

       s=(y1+4.d0*y2+2.d0*y3)*h/3.d0

    elseif(trim(method).eq."simpson38")then

       if(mod(N,3).ne.1)then
          write(6,*)"=====cannot calculation with simpson38"
          write(6,*)"=====program stop"
          stop
       endif

       y0=y(1)+y(N)
       do i=2,N-2,3
          y1=y1+y(i)
       enddo
       do i=3,N-1,3
          y2=y2+y(i)
       enddo
       do i=4,N-3,3
          y3=y3+y(i)
       enddo
       s=(y0+3.d0*(y1+y2)+2.d0*y3)*3.d0*h/8.d0        

    elseif(trim(method).eq."boole")then
       if(mod(N,4).ne.1)then
          write(6,*)"=====cannot calculation with boole"
          write(6,*)"=====program stop"
          stop
       endif

       y0=y(1)+y(N)
       do i=5,N-4,4
          y1=y1+y(i)
       enddo
       do i=2,N-1,2
          y2=y2+y(i)
       enddo
       do i=3,N-2,4
          y3=y3+y(i)
       enddo

       s=(14.d0*y0+28.d0*y1+64.d0*y2+24.d0*y3)*h/45.d0
    else
       write(6,*)"=====cannot calculation in integral"
       write(6,*)"=====program stop"
       stop
    end if

    return
  end subroutine dintegral
 
  subroutine dintegral2d(Nx,Ny,z,hx,hy,s,method)
    implicit none
    integer,intent(in)::Nx,Ny
    double precision,intent(in)::hx,hy,z(1:Nx,1:Ny)
    character(*),intent(in)::method
    double precision,intent(out)::s
    integer::i
    double precision::ty(1:Ny),r(1:Nx)

    s=0.d0
    ty(1:Ny)=0.d0
    r(1:Nx)=0.d0
    do i=1,Nx
       ty(1:Ny)=z(i,1:Ny)
       call integral(Ny,ty,hy,s,method)
       r(i)=s
    enddo
    call integral(Nx,r,hx,s,method)
       
    return
  end subroutine dintegral2d
 
  subroutine dintegral3d(Nx,Ny,Nz,w,hx,hy,hz,s,method)
    implicit none
    integer,intent(in)::Nx,Ny,Nz
    double precision,intent(in)::hx,hy,hz,w(1:Nx,1:Ny,1:Nz)
    character(*),intent(in)::method
    double precision,intent(out)::s
    integer::i
    double precision::tyz(1:Ny,1:Nz),r(1:Nx)
       
    s=0.d0
    tyz(1:Ny,1:Nz)=0.d0
    r(1:Nx)=0.d0
    do i=1,Nx
       tyz(1:Ny,1:Nz)=w(i,1:Ny,1:Nz)
       call integral(Ny,Nz,tyz,hy,hz,s,method)
       r(i)=s
    enddo
    call integral(Nx,r,hx,s,method)    
       
    return
  end subroutine dintegral3d
 
  subroutine cintegral(N,y,h,s,method)
    integer,intent(in)::N
    complex(kind(0d0)),intent(in)::y(1:N)
    double precision,intent(in)::h
    character(*),intent(in)::method
    complex(kind(0d0)),intent(out)::s

    double precision::res,ims

    s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0

    call integral(N,dble(y),h,res,trim(method))
    call integral(N,dimag(y),h,ims,trim(method))
   
    s=dcmplx(res,ims)
   
    return
  end subroutine cintegral

  subroutine cintegral2d(Nx,Ny,z,hx,hy,s,method)
    integer,intent(in)::Nx,Ny
    complex(kind(0d0)),intent(in)::z(1:Nx,1:Ny)
    double precision,intent(in)::hx,hy
    character(*),intent(in)::method
    complex(kind(0d0)),intent(out)::s

    double precision::res,ims

    s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0

    call integral(Nx,Ny,dble(z),hx,hy,res,trim(method))
    call integral(Nx,Ny,dimag(z),hx,hy,ims,trim(method))
   
    s=dcmplx(res,ims)
   
    return
  end subroutine cintegral2d

  subroutine cintegral3d(Nx,Ny,Nz,w,hx,hy,hz,s,method)
    integer,intent(in)::Nx,Ny,Nz
    complex(kind(0d0)),intent(in)::w(1:Nx,1:Ny,1:Nz)
    double precision,intent(in)::hx,hy,hz
    character(*),intent(in)::method
    complex(kind(0d0)),intent(out)::s

    double precision::res,ims

    s=dcmplx(0d0,0d0); res=0.d0; ims=0.d0

    call integral(Nx,Ny,Nz,dble(w),hx,hy,hz,res,trim(method))
    call integral(Nx,Ny,Nz,dimag(w),hx,hy,hz,ims,trim(method))
   
    s=dcmplx(res,ims)
   
    return
  end subroutine cintegral3d
end module integral_mod

サブルーチン”integral”を用いた例題

実際の使い方。参考にどうぞ。
下のコードは2次元の積分
\(
\displaystyle \int\int xe^{-x^2}e^{-y}dxdy=\frac{e^{-x^2}}{2}e^{-y}+\mbox{const}
\)
を数値積分します。積分範囲を\(x=0\sim 3, \; y=0 \sim 5\)にした場合、その解析解は
\(
\begin{align}
\int_0^3 dx\int_0^5 dy xe^{-x^2}e^{-y}&=\frac{1}{2}(1-e^{-5}-e^{-9}+e^{-14})\\
&=0.4965697373627734784608751894356320535936864348993604\cdots
\end{align}
\)
となります。実行すると

./a.out
simpson   :    0.496569737366759E+000
romberg,3 :    0.496569737362773E+000

となります。コードは、

program main
  use integral_mod
  implicit none
  integer::i,j,n,Nx,Ny
  double precision::hx,hy,ans
  double precision::xmin,xmax,ymin,ymax
  double precision,allocatable::x(:),y(:)
  double precision::s
  double precision,allocatable::w(:,:)
  double precision::f
  external::f
 
  n=10

  xmin=0d0
  xmax=3d0

  ymin=0d0
  ymax=5d0

  Nx=2**(n)
  Ny=2**(n)
  allocate(x(0:Nx),y(0:Ny),w(0:Nx,0:Ny))
  x=0d0; y=0d0; w=dcmplx(0d0,0d0)

  hx=(xmax-xmin)/dble(Nx)
  hy=(ymax-ymin)/dble(Ny)
 
  do i=0,Nx
     x(i)=xmin+hx*dble(i)
  enddo
  do i=0,Ny
     y(i)=ymin+hy*dble(i)
  enddo

  do i=0,Nx
     do j=0,Ny
        w(i,j)=f(x(i),y(j))
     end do
  end do

  call integral(size(w,1),size(w,2),w,hx,hy,s,"simpson")
  write(6,'(A,e25.15e3)')"simpson   : ",s
 
  call integral(size(w,1),size(w,2),w,hx,hy,s,"romberg",3)
  write(6,'(A,e25.15e3)')"romberg,3 : ",s
 
  return
end program main

function f(x,y)
  implicit none
  double precision,intent(in)::x,y
  double precision::f
 
  f=x*exp(-x*x)*exp(-y)
 
  return
end function f

3次元の計算の例題です。
下のコードは
\(
\displaystyle \int\int\int x^4y^4z^4 dxdydz=\left(\frac{1}{5}\{0.7^5-(-1)^5\}\right)^3
\)
を数値積分します。積分範囲を\(x,y,z=-1\sim 0.7\)にした場合、その値は
\(
\displaystyle \int_{-1}^{0.7}\int_{-1}^{0.7}\int_{-1}^{0.7} x^4y^4z^4 dxdydz = 0.127496010896795\cdots
\)
となります。実行すると、

$ gfortran integralmod.f90 main.f90
$ ./a.out
analysis  :   0.127496010896795E-01
simpson   :   0.10507613E-006  0.10507613E-006
romberg,3 :  -0.17347235E-017 -0.17347235E-017

と得られます。中身はこうです。分点の数はx,y,z軸各々で違っていて構いません。

program main
  use integral_mod
  implicit none
  integer::i,j,k,n,Nx,Ny,Nz
  double precision::hx,hy,hz,ans
  double precision,allocatable::x(:),y(:),z(:)
  complex(kind(0d0))::s
  complex(kind(0d0)),allocatable::w(:,:,:)
 
  n=6
  Nx=2**(n)
  Ny=2**(n-1)
  Nz=2**(n+1)
 
  allocate(x(0:Nx),y(0:Ny),z(0:Nz),w(0:Nx,0:Ny,0:Nz))
  x=0d0; y=0d0; z=0d0; w=dcmplx(0d0,0d0)
 
  hx=1.7d0/dble(size(w,1)-1)
  hy=1.7d0/dble(size(w,2)-1)
  hz=1.7d0/dble(size(w,3)-1)
 
  do i=0,Nx
     x(i)=hx*dble(i)-1d0
  enddo
  do i=0,Ny
     y(i)=hy*dble(i)-1d0
  enddo
  do i=0,Nz
     z(i)=hz*dble(i)-1d0
  enddo

  do i=0,Nx
     do j=0,Ny
        do k=0,Nz
           w(i,j,k)=dcmplx((x(i)*y(j)*z(k))**4,(x(i)*y(j)*z(k))**4)
        end do
     end do
  end do

  ans=(0.7d0**5.d0+1.d0)/5.d0
  ans=ans**3.d0
  write(6,'(A,e23.15e2)')"analysis  : ",ans
 
  call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"simpson")
  write(6,'(A,2e17.8e3)')"simpson   : ",dble(s)-ans,dimag(s)-ans
 
  call integral(size(w,1),size(w,2),size(w,3),w,hx,hy,hz,s,"romberg",3)
  write(6,'(A,2e17.8e3)')"romberg,3 : ",dble(s)-ans,dimag(s)-ans
 
  return
end program main

ロンバーグ積分のプログラム

ロンバーグ積分
 call romberg(jx,x,y,s,pre)
 配列yの大きさは2,3,5,10,…,\(2^{jx}+1\)個でないといけない ロンバーグ積分では収束精度”pre”を指定すること。もしも収束精度に達しなかった場合、警告と共に、与えられた値での収束限界の積分結果を返す。積分精度を高めたければ刻み幅を小さくする操作(例えば分点数を増やす等)をしてください。”pre”は、積分結果の絶対値が1より大きくなる場合は相対誤差を、小さくなる場合は絶対誤差を取ります。この理由は以前の結果の補正を加え、収束をさせるためであり、非常に小さい誤差の場合いつまでたっても機械誤差のため収束しないからです。
module romberg_mod
  !developer --> sikino
  !date --> 2016/03/01
  !         2016/03/03
  !
  ! 1D case :
  !  romberg(jx,x,y,s,pre)
  !          |  | | | +- (in)  precision (e.g. 1d-8)
  !          |  | | +--- (out) integration result
  !          |  | +----- (in)  y(1:2**jx+1) f(x)
  !          |  +------- (in)  x(1:2**jx+1) x
  !          +---------- (in)  related to array size
  !
  ! 2D case :
  !  romberg(jx,jy,x,y,z,s,pre)
  !          |  |  | | | | +-- (in)  precision (e.g. 1d-8)
  !          |  |  | | | +---- (out) integration result
  !          |  |  | | +------ (in)  z(1:2**jx+1,1:2**jy+1) f(x,y)
  !          |  |  | +-------- (in)  y(1:2**jy+1) y
  !          |  |  +---------- (in)  x(1:2**jx+1) x
  !          |  +------------- (in)  related to array size y
  !          +---------------- (in)  related to array size x
  !
  ! 3D case :
  !  romberg(jx,jy,jz,x,y,z,w,s,pre)
  !          |  |  |  | | | | | +-- (in)  precision (e.g. 1d-8)
  !          |  |  |  | | | | +---- (out) integration result
  !          |  |  |  | | | +------ (in)  w(1:2**jx+1,1:2**jy+1,1:2**jz+1) f(x,y,z)
  !          |  |  |  | | +-------- (in)  z(1:2**jz+1) z
  !          |  |  |  | +---------- (in)  y(1:2**jy+1) y
  !          |  |  |  +------------ (in)  x(1:2**jx+1) x
  !          |  |  +--------------- (in)  related to array size z
  !          |  +------------------ (in)  related to array size y
  !          +--------------------- (in)  related to array size x
  !
  implicit none
  interface romberg
     module procedure &
          dromberg, &
          dromberg2d, &
          dromberg3d
  end interface romberg
contains
  subroutine dromberg(jx,x,y,s,pre)
    implicit none
    integer,intent(in)::jx
    double precision,intent(in)::x(1:2**jx+1),y(1:2**jx+1),pre
    double precision,intent(out)::s

    integer,parameter::jm=6 !--> precision: O(h^(2*jm))
    integer,parameter::nm=2**jm
    double precision,allocatable::tx(:),ty(:)
    double precision::ts
    integer::k

    s=0d0
    if(jx.ge.jm)then
       allocate(tx(1:nm+1),ty(1:nm+1)); tx=0d0; ty=0d0
       do k=0,2**(jx-jm)-1
          ts=0d0
          tx(1:nm+1)=x(k*nm+1:(k+1)*nm+1)
          ty(1:nm+1)=y(k*nm+1:(k+1)*nm+1)

          call romberg_sub(jm,tx,ty,ts,pre)
          s=s+ts
       enddo
       deallocate(tx,ty)    
    else
       call romberg_sub(jx,x,y,s,pre)
    endif

    return
  end subroutine dromberg

  subroutine romberg_sub(jx,x,y,s,pre)
    ! reference "http://www.math.usm.edu/lambers/mat460/fall09/lecture29.pdf"
    implicit none
    integer,intent(in)::jx
    double precision,intent(in)::x(1:2**jx+1),y(1:2**jx+1),pre
    double precision,intent(out)::s

    integer::i,j,k,n,dn
    double precision::h,ps,tmp
    double precision::T(1:jx+1,1:jx+1)

    n=2**jx+1

    h=x(n)-x(1)
    dn=(n-1)/2

    T(1,1)=0.5d0*h*(y(1)+y(n))
    s=T(1,1)
    ps=s
    h=0.5d0*h
    do j=2,jx+1

       ! trapezoidal rule
       tmp=0d0
       do i=1,2**(j-2)
          tmp=tmp+y(1+(2*i-1)*(dn))
       enddo
       T(j,1)=0.5d0*T(j-1,1)+h*tmp

       do k=2,j
          ! Richardson extrapolation
          T(j,k)=T(j,k-1)+(T(j,k-1)-T(j-1,k-1))/(dble(4**(k-1))-1d0)
       enddo
       s=T(j,j)

       ! precision check
       if(abs(s).ge.1d0)then
          if(abs((ps-s)/s).le.pre)exit
       else
          if(abs((ps-s)).le.pre)exit
       endif
       ps=s
       h=0.5d0*h
       dn=dn/2
    enddo

    if(j-1.eq.jx)then
       write(6,'(A)')" -+-+- didn't converge at romberg integral -+-+- "
       write(6,'(A)')"       Please change stepsize h of array x  "
    endif

    return
  end subroutine romberg_sub

  subroutine dromberg2d(jx,jy,x,y,z,s,pre)
    implicit none
    integer,intent(in)::jx,jy
    double precision,intent(in)::pre,x(1:2**jx+1),y(1:2**jy+1)
    double precision,intent(in)::z(1:2**jx+1,1:2**jy+1)
    double precision,intent(out)::s

    integer::i,nx,ny
    double precision::ty(1:2**jy+1),r(1:2**jx+1)
    nx=2**jx+1
    ny=2**jy+1

    s=0.d0
    ty(1:ny)=0.d0
    r(1:nx)=0.d0
    do i=1,nx
       ty(1:ny)=z(i,1:ny)
       call romberg(jy,y,ty,s,pre)
       r(i)=s
    enddo
    call romberg(jx,x,r,s,pre)
       
    return
  end subroutine dromberg2d
 
  subroutine dromberg3d(jx,jy,jz,x,y,z,w,s,pre)
    implicit none
    integer,intent(in)::jx,jy,jz
    double precision,intent(in)::pre,x(1:2**jx+1),y(1:2**jy+1),z(1:2**jz+1)
    double precision,intent(in)::w(1:2**jx+1,1:2**jy+1,1:2**jz+1)
    double precision,intent(out)::s
    integer::i,nx,ny,nz
    double precision::tyz(1:2**jy+1,1:2**jz+1),r(1:2**jx+1)
       
    nx=2**jx+1; ny=2**jy+1; nz=2**jz+1
    s=0.d0
    tyz(1:ny,1:nz)=0.d0
    r(1:nx)=0.d0
    do i=1,nx
       tyz(1:ny,1:nz)=w(i,1:ny,1:nz)
       call romberg(jy,jz,y,z,tyz,s,pre)
       r(i)=s
    enddo
    call romberg(jx,x,r,s,pre)  
       
    return
  end subroutine dromberg3d
end module romberg_mod

ロンバーグ積分(romberg_mod)の例

必要なのは、上で紹介したモジュール “romberg_mod” と下のメインプログラムです。
以下のプログラムは1次元の定積分
\(
\int_1^10 \frac{1}{x^2} dx = 0.9
\)
を分点数\(2^8+1(jx=8)\)個でロンバーグ積分するものです。
精度は\(O(h^{2\cdot min{jm,jx}})\)です。
ここで\(jm\)はモジュールromberg_modの中にパラメータとして宣言されています。

コンパイルは

ifort romberg_mod.f90 main.f90

とでもすればいいでしょう。

program main
  use romberg_mod
  implicit none
  integer::i,jx,n
  double precision::h,a,b,s
  double precision,allocatable::x(:),y(:)
  double precision::f
  external::f
 
  a=1d0
  b=10d0
  jx=8
  n=2**jx+1
  allocate(x(1:n),y(1:n))
  h=(b-a)/dble(n-1)
  do i=1,n
     x(i)=a+h*dble(i-1)
     y(i)=f(x(i))
  enddo
 
  call romberg(jx,x,y,s,1d-8)
  write(6,*)s,"romberg"
 
  stop
end program main

function f(x)
  implicit none
  double precision::f,x
 
  f=1d0/(x*x)
 
  return
end function f

実行例(要求精度は\(10^{-8}\))

>./a.out
  0.900000000062642  
>

2次元ではこう。

program main
  use romberg_mod
  implicit none
  integer::i,j,Nx,Ny,jx,jy
  double precision::hx,hy
  double precision::xmin,xmax,ymin,ymax
  double precision,allocatable::x(:),y(:)
  double precision::s
  double precision,allocatable::w(:,:)
  double precision::f
  external::f
 
  jx=10
  jy=8
  xmin=0d0
  xmax=3d0

  ymin=0d0
  ymax=5d0

  Nx=2**(jx)
  Ny=2**(jy)
  allocate(x(0:Nx),y(0:Ny),w(0:Nx,0:Ny))
  x=0d0; y=0d0; w=dcmplx(0d0,0d0)

  hx=(xmax-xmin)/dble(Nx)
  hy=(ymax-ymin)/dble(Ny)
 
  do i=0,Nx
     x(i)=xmin+hx*dble(i)
  enddo
  do i=0,Ny
     y(i)=ymin+hy*dble(i)
  enddo

  do i=0,Nx
     do j=0,Ny
        w(i,j)=f(x(i),y(j))
     end do
  end do

  call romberg(jx,jy,x,y,w,s,1d-8)
  write(6,*)s
 
  stop
end program main

function f(x,y)
  implicit none
  double precision,intent(in)::x,y
  double precision::f
 
  f=x*exp(-x*x)*exp(-y)
 
  return
end function f

実行例

>./a.out
  0.496569737374163
>

[adsense2]

WordPress

HTMLで行間をちょっとだけ開ける?

コメントする

HTMLで行間を半行開けたい！
そう思ったのが始まりでした。が！
無理らしいです。CSSでやらないといけないみたいです。
まず、通常の改行<br />によって開けると、
———————–
AAA
AAA

AAA

AAA
AAA
———————–
のようにかなりの幅が開いてしまいます。これを
———————–
AAA
AAA
AAA
AAA
AAA
———————–
のように開けます。

ここでやっているのは半行開けるのではなく、行に２倍の広さを持たせて、その中央に文字を書く、ということを行っているのです。

すなわち、
<br /> AAA <br />
によって改行をあけるのではなく、
<span style=”line-height:200%;”>AAA</span>
と書くことです。

イメージとしては

な感じです。

プログラミングと数値計算

ファイル読み込み

コメントする

ファイルの読み込みに関するサブルーチンを記述します。

 do i=1,4
     do j=1,83
        write(30,*)i,j,i*j
     end do
     write(30,*)
  end do

によってファイル”fort.30″が作られたとします。
今、fort.30を読み込んで
“i”の数”4”
と
“j”の数”83″
を取り出したいとします。

read文を使って読み込みますが、そのまま読み込むと空白部分を読み込んだり、読み込まないだったりします。
ここでは上のdoループによって作られたファイルの場合に使えるものを想定します。

ここでは、
大きな塊を表す数である”4″をblock,
塊の中の要素数を表す”83″をelement
と呼ぶことにします。

この問題を解く戦略は、ファイルを読み込む2種類の方法です。
1つは本当の行数(空行含む)を数え、もう1つは空行を飛ばして読み込む方法です。
本当の行数を数えるサブルーチンは下の”linecount”
であり、
空行を読み飛ばして行数を数えるサブルーチンは下の”linecount_eff”
です。
この二つと、一番下の行に追加される余分な１行を対処するために”breaklinecheck”というルーチンを使います。

これによってblockとelementを出力するサブルーチン”blockelement”を作っています。

下のプログラムを実行すると

$ gfortran main.f90
$ ./a.out
 ===Apply for fortran file will done===
 Nblock     ::         4
 Nelement   ::        83

という結果が得られるかと思います。

program main
  !developer => sikinote
  !date      => 2015/03/31
  implicit none
  integer::NBlock,Nelement
  character(48)::filename
 
  filename='./fort.30'
  call blockelement(filename,Nblock,Nelement)

  write(6,'(A,i10)')" Nblock     ::",Nblock
  write(6,'(A,i10)')" Nelement   ::",Nelement

  stop
end program
!===================================
   
subroutine blockelement(filename,Nblock,Nelement)
  !developer => sikino
  !date      => 2015/03/31
  implicit none
  character(*),intent(in)::filename
  integer,intent(out)::Nblock,Nelement
  integer::c1,c2
 
  call linecount(c1,filename)
  call linecount_eff(c2,filename)
  call breaklinecheck(c1,c2)
  Nblock=c1-c2+1
  Nelement=c2/Nblock
 
  return
end subroutine blockelement
!------------------------------
subroutine linecount(c,filename)
  implicit none
  integer,intent(out)::c
  character(*),intent(in)::filename

  integer::ier
  character(len_trim(filename))::fname
 
  fname=trim(filename)
  c=0
  open(100,file=fname,status='old',iostat=ier,err=990)
  do while(.true.)
     read(100,*,end=999)
     c=c+1
  enddo
999 continue
  close(100)
   
  return
!+-----------------------+
990 write(6,'(A)')"!!!!==error when open file",trim(fname),"info-->",ier
  write(6,*)"======program stop at linecount"
  stop

end subroutine linecount
!--------------------------------
subroutine linecount_eff(c,filename)
  implicit none
  integer,intent(out)::c
  character(*),intent(in)::filename

  integer::ier
  character(100)::cc
  character(len_trim(filename))::fname
 
  fname=trim(filename)

  c=0
  open(100,file=fname,status='old',iostat=ier,err=990)
  do while(.true.)
     read(100,*,end=998)cc
     if(len_trim(cc).gt.0)c=c+1
  enddo

998 continue
  close(100)
  return

990 write(6,'(A)')"!!!!==error when open file",trim(fname),"info==>",ier
  write(6,*)"======program stop at linecount_eff"
  stop

end subroutine linecount_eff
!-------------------------------------
subroutine breaklinecheck(c1,c2)
  implicit none
  integer,intent(inout)::c1
  integer,intent(in)::c2
  integer::Nb
 
  Nb=c1-c2+1
  if(Nb.eq.2.or.mod(c2,Nb).ne.0)then
     write(6,*)"===Apply for fortran file will done==="
     c1=c1-1
     Nb=c1-c2+1
     if(mod(c2,Nb).ne.0)then
        write(6,*)"line is different(may be last break)"
        write(6,*)"program stop at subroutine __breaklinecheck__"
        stop
     end if
  endif
 
  return
end subroutine breaklinecheck

データを読み込むには？

さて、ブロックの数と要素の数が上のサブルーチンを使うことにより求められることがわかりました。
実際にデータを配列に代入するためにはどうすればいいんでしょう？
型に応じて使うサブルーチンを変えます。
その手続きは下のモジュールを記述することでokです。これを書いた上で、
メインプログラムを以下のように書きます。そうすれば配列x(,)とy(,)に値がはいります。

program main
  use read1
  implicit none
  integer::NBlock,Nelement,i,j
  character(48)::filename
 
  double precision,allocatable::x(:,:),y(:,:)
 
  filename='./fort.30'
  call blockelement(filename,Nblock,Nelement)

  write(6,'(A,i10)')" Nblock     ::",Nblock
  write(6,'(A,i10)')" Nelement   ::",Nelement
 
  allocate(x(1:Nblock,1:Nelement),y(1:Nblock,1:Nelement))
  call read_filedata(size(y,1),size(y,2),x,y,filename)
 
  do i=1,Nblock
     do j=1,Nelement
        write(11,*)x(i,j),y(i,j)
     enddo
     write(11,*)
  enddo
 
  stop
end program

総称名を用いる場合の手続き(read_filedata())

module read1
  implicit none
  interface read_filedata
     module procedure &
          ! dx1 -> double precision array, x(:)
          ! cy2 -> complex array, y(:,:)
          ! xyy -> coloum of file, | x y y |
          read_dx0_dy1_xy, &
          read_dx0_cy1_xyy, &
          read_dx1_dy1_xy, &
          read_dx1_cy1_xyy, &
          read_dx1_dy2_xy, &
          read_dx1_cy2_xyy, &
          read_dx2_dy2_xy, &
          read_dx2_cy2_xyy
  end interface read_filedata
contains
  subroutine read_dx0_dy1_xy(Ne,y,place,col12)
    integer,intent(in)::Ne,col12
    character(*),intent(in)::place
    double precision,intent(out)::y(1:Ne)

    integer::i,ier
    double precision::a,b
    character(len_trim(place))::fn

    y=0d0
    fn=trim(place)

    open(28,file=fn,status='old',iostat=ier,err=977)
    if(col12.eq.1)then
       do i=1,Ne
          read(28,*)a,b
          y(i)=a
       enddo
    elseif(col12.eq.2)then
       do i=1,Ne
          read(28,*)a,b
          y(i)=b
       enddo
    else
       go to 977
    endif
             
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx0_dy1_11"
    stop
  end subroutine read_dx0_dy1_xy

  subroutine read_dx0_cy1_xyy(Ne,y,place)
    integer,intent(in)::Ne
    character(*),intent(in)::place
    complex(kind(0d0)),intent(out)::y(1:Ne)

    integer::i,ier
    double precision::a,b,c
    character(len_trim(place))::fn

    y=0d0
    fn=trim(place)

    open(28,file=fn,status='old',iostat=ier,err=977)
    do i=1,Ne
       read(28,*)a,b,c
       y(i)=dcmplx(b,c)
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx0_cy1_xyy"
    stop
  end subroutine read_dx0_cy1_xyy

  subroutine read_dx1_dy1_xy(Ne,x,y,place)
    integer,intent(in)::Ne
    character(*),intent(in)::place
    double precision,intent(out)::x(1:Ne),y(1:Ne)

    character(len_trim(place))::fn
    double precision::a,b
    integer::i,ier

    x=0d0; y=0d0
   
    fn=trim(place)
    open(28,file=trim(fn),status='old',iostat=ier,err=977)
    do i=1,Ne
       read(28,*)a,b
       x(i)=a
       y(i)=b
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx1_dy1_xy"
    stop
  end subroutine read_dx1_dy1_xy
 
  subroutine read_dx1_cy1_xyy(Ne,x,y,place)
    integer,intent(in)::Ne
    character(*),intent(in)::place
    double precision,intent(out)::x(1:Ne)
    complex(kind(0d0)),intent(out)::y(1:Ne)

    integer::i,ier
    double precision::a,b,c
    character(len_trim(place))::fn

    y=0d0
    fn=trim(place)

    open(28,file=fn,status='old',iostat=ier,err=977)
    do i=1,Ne
       read(28,*)a,b,c
       x(i)=a
       y(i)=dcmplx(b,c)
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx1_cy1_xyy"
    stop
  end subroutine read_dx1_cy1_xyy

  subroutine read_dx1_dy2_xy(Nb,Ne,x,y,place)
    integer,intent(in)::Nb,Ne
    double precision,intent(out)::x(1:Ne),y(1:Nb,1:Ne)
    character(*),intent(in)::place
   
    integer::i,j,ier
    character(len_trim(place))::fn
    double precision::a,b
   
    x=0d0; y=0d0
   
    fn=trim(place)
    open(28,file=trim(fn),status='old',iostat=ier,err=977)
    do i=1,Nb
       do j=1,Ne
          read(28,*)a,b
          if(i.eq.1)x(j)=a
          y(i,j)=b
       enddo
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx1_dy2_xy"
    stop
  end subroutine read_dx1_dy2_xy
 
  subroutine read_dx1_cy2_xyy(Nb,Ne,x,y,place)
    integer,intent(in)::Nb,Ne
    double precision,intent(out)::x(1:Ne)
    complex(kind(0d0)),intent(out)::y(1:Nb,1:Ne)
    character(*),intent(in)::place

    integer::i,j,ier
    character(len_trim(place))::fn
    double precision::a,b,c

    x=0d0; y=0d0

    fn=trim(place)
    open(28,file=trim(fn),status='old',iostat=ier,err=977)
    do i=1,Nb
       do j=1,Ne
          read(28,*)a,b,c
          if(i.eq.1)x(j)=a
          y(i,j)=dcmplx(b,c)
       enddo
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx1_cy2_12"
    stop
  end subroutine read_dx1_cy2_xyy

  subroutine read_dx2_dy2_xy(Nb,Ne,x,y,place)
    integer,intent(in)::Nb,Ne
    double precision,intent(out)::x(1:Nb,1:Ne),y(1:Nb,1:Ne)
    character(*),intent(in)::place
   
    integer::i,j,ier
    character(len_trim(place))::fn
    double precision::a,b
   
    x=0d0; y=0d0
   
    fn=trim(place)
    open(28,file=trim(fn),status='old',iostat=ier,err=977)
    do i=1,Nb
       do j=1,Ne
          read(28,*)a,b
          x(i,j)=a
          y(i,j)=b
       enddo
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx2_dy2_11"
    stop
  end subroutine read_dx2_dy2_xy

  subroutine read_dx2_cy2_xyy(Nb,Ne,x,y,place)
    integer,intent(in)::Nb,Ne
    double precision,intent(out)::x(1:Nb,1:Ne)
    complex(kind(0d0))::y(1:Nb,1:Ne)
    character(*),intent(in)::place
   
    integer::i,j,ier
    character(len_trim(place))::fn
    double precision::a,b,c
   
    x=0d0; y=dcmplx(0d0,0d0)
   
    fn=trim(place)
    open(28,file=trim(fn),status='old',iostat=ier,err=977)
    do i=1,Nb
       do j=1,Ne
          read(28,*)a,b,c
          x(i,j)=a
          y(i,j)=dcmplx(b,c)
       enddo
    enddo
    close(28)
    return

977 write(6,'(3A,i5)')"!!!!==error when open file",trim(fn),"info==>",ier
    write(6,*)"======program stop at read_dx2_cy2_12"
    stop
  end subroutine read_dx2_cy2_xyy
end module read1
数学, 物理学

ラグランジュの未定乗数法

コメントする

忘れやすいラグランジュの未定乗数法のメモです。
一通り学んだ人が使い方を思い出す、という状況を想定しています。

変数が独立な場合

3変数x,y,zが独立(xが変化してもy,zは変化しない、\(\vec{x}\cdot\vec{y}=0\) (y,zも同様))で、その関数\(f(x,y,z)\)の極値は
\(
\displaystyle \frac{\partial f}{\partial x}=0,\ \ \frac{\partial f}{\partial y}=0,\ \ \frac{\partial f}{\partial z}=0 \ \ \cdots (1)
\)
を連立させて解くことで得られます。

変数が独立ではない(従属な)場合

変数x,y,zの間に関係式
\(
g(x,y,z)=c, \ \mbox{$c$は定数} \ \ \cdots (2)
\)
という条件がある場合、

  1. 式(2)が(例えば)zについて解けるならば、\(f(x,y,z(x,y))\)として2変数\(x,y\)の極値問題として解ける。
  2. \(z=z(x,y)\)の形に書けない場合 →ラグランジュの未定乗数法を使う
  1.  の場合、”関数\(f(x,y,z)\)が極値をとる”、とは
    \(
    \displaystyle df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz=0 \ \ \cdots (3)
    \)
    である点(極値点)である。
    →極値点から\(x,y,z\)を任意の微小量\(dx,dy,dz\)だけ変化させても関数\(f(x,y,z)\)の変化分である\(df\)は1次の範囲でゼロです。
    故に任意の\(dx,dy,dz\)について(3)が成立する、よって(1)が導かれることになります。

  2.  の場合、\(dx,dy,dz\)は独立に選ぶことができません。その取り方は条件(2)に従います。
    極値点まわりで(2)が成立しているならば、
    \(
    g(x+dx,y+dy,z+dz)=g(x,y,z)\ \ \cdots (4)
    \)
    を満たすような\(dx,dy,dz\)の変化しか許されないことになります。この条件から\(dx,dy,dz\)の動かし方は、
    \(
    \displaystyle \frac{\partial g}{\partial x}dx+\frac{\partial g}{\partial y}dy+\frac{\partial g}{\partial z}dz=0 \ \ \cdots (5)
    \)
    に制限されます。
    条件(5)を\(dz\)について変形すると、
    \(
    \displaystyle dz=-\frac{\frac{\partial g}{\partial x}dx+\frac{\partial g}{\partial y}dy}{\frac{\partial g}{\partial z}} \ \ \cdots (6)
    \)
    となります。式(3)へ式(6)を代入すると

    \(
    \begin{align}
    \displaystyle df &=\left( \frac{\partial f}{\partial x}-\frac{\frac{\partial g}{\partial x}}{\frac{\partial g}{\partial z}}\frac{\partial f}{\partial z}\right)dx
    +\left( \frac{\partial f}{\partial y}-\frac{\frac{\partial g}{\partial y}}{\frac{\partial g}{\partial z}}\frac{\partial f}{\partial z}\right)dy=0 \\
    &=\left( \frac{\partial f}{\partial x}-\lambda\frac{\partial g}{\partial x}\right)dx
    +\left( \frac{\partial f}{\partial y}-\lambda\frac{\partial g}{\partial y}\right)dy=0 \ \ \cdots (7)
    \end{align}
    \)

    ここで
    \(
    \displaystyle \lambda=\frac{\frac{\partial f}{\partial z}}{\frac{\partial g}{\partial z}}\ \ \cdots (8)
    \)
    と置きました。この\(\lambda\)はラグランジュの未定乗数と呼ばれます。
    未定乗数という所以は、この\(\lambda\)をあらわに決める必要はなく、決まらない定数のままでも極値点を求めることができるという事を表しています。
    今、\(dx,dy\)は独立であるので(※1)、その係数は\(0\)になるはずです。故に、式(7)と式(8)より、

    \(
    \begin{eqnarray}
    \left\{
    \begin{aligned}
    \frac{\partial f}{\partial x}-\lambda\frac{\partial g}{\partial x}&=0 \\
    \frac{\partial f}{\partial y}-\lambda\frac{\partial g}{\partial y}&=0 \\
    \frac{\partial f}{\partial z}-\lambda\frac{\partial g}{\partial z}&=0
    \end{aligned}
    \right.
    \end{eqnarray}
    \)

    が導けます。変形をすれば、条件式(2)も含めて、

    \(
    \begin{eqnarray}
    \left\{
    \begin{aligned}
    \frac{\partial}{\partial x}\left(f-\lambda g\right)&=0 \\
    \frac{\partial}{\partial y}\left(f-\lambda g\right)&=0 \\
    \frac{\partial}{\partial z}\left(f-\lambda g\right)&=0 \\
    g(x,y,z)&=c
    \end{aligned}
    \right.
    \end{eqnarray}
    \ \ \ \cdots (9)
    \)

    と書くことができます。未知の変数は\(x,y,z,\lambda\)の4つで、方程式は4本なので解くことができます。
    この式が言うことは、束縛条件\(g(x,y,z)=c\)があった場合、関数\(f-\lambda g\)を考えて、その極値を求めればよいことを表しています。

[adsense1]

まとめ

条件\(g(x,y,z)=c\)がある関数f(x,y,z)の極値問題は、
\(
\tilde{f}=f-\lambda g \ \ \cdots (10)
\)
という新たな関数\(\tilde{f}\)を考えるとx,y,zが独立に変化するものと考えて\(\tilde{f}(x,y,z)\)の極値問題を考えればよい、となります。

例題 ~楕円に内接する長方形の面積の最大値を求める~

楕円の方程式は
\(
\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\)
であり、この方程式の許す\(x,y\)を満たしながら、内接する長方形の面積
\(S(x,y)=4xy\)
を最大にする\(x,y\)を求めます。

楕円面積

これは、関数\(f(x,y)=4xy\)の極値を\(\displaystyle g(x,y)=\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)という条件下で解く、という意味になります。
まず、\(\tilde{S}\)を式(10)より求めます。
\(
\begin{align}
\tilde{S}&=S-\lambda g \\
&=4xy-\lambda\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}\right)
\end{align}
\)
式(9)より、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial \tilde{S}}{\partial x}&=0 \\
\frac{\partial \tilde{S}}{\partial y}&=0
\end{aligned}
\right.
\end{eqnarray}
\)
を考えればいいので、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial \tilde{S}}{\partial x}=4y-\lambda \frac{2x}{a^2}&=0 \ \ \cdots (i)\\
\frac{\partial \tilde{S}}{\partial y}=4x-\lambda \frac{2y}{b^2}&=0 \ \ \cdots (ii)\\
\frac{x^2}{a^2}+\frac{y^2}{b^2}&=1 \ \ \cdots (iii)
\end{aligned}
\right.
\end{eqnarray}
\)
を満たす未知の変数\(x,y,\lambda\)が\(S\)の極値となっています。
(i)と(ii)より\(\lambda\)を消去すると
\(
\begin{align}
(i) &\rightarrow \lambda=\frac{2y}{x}a^2 \\
(ii) &\rightarrow 4x-\left(\frac{2y}{x}a^2\right)\frac{2y}{b^2}=0
\end{align}
\)
なので
\(
\displaystyle \frac{x^2}{a^2}=\frac{y^2}{b^2}
\)
(iii)に代入して
\(
\displaystyle 2\frac{x^2}{a^2}=1
\)
より
\(\displaystyle x=\pm\frac{a}{\sqrt{2}},\ \ y=\pm\frac{b}{\sqrt{2}}\)
のとき\(S(x,y)\)が極値を取ることがわかります。

ちなみに、この時の長方形の面積\(S_{max}\)は\(S_{max}=2ab\)であり、
これは楕円の面積\(S=\pi ab\)の\(\frac{2ab}{\pi ab}\sim 0.64\)となり、約64%を占めていることになります。

[adsense2]

※1
x,yが独立であるのは、x,y,zをつなぐ1本の条件式\(g(x,y,z)=c\)によって消え得る変数は1つだけであるためです。

参考

小野寺 嘉孝著 『物理のための応用数学』裳華房(1988)p.6~10

物理学

振り子

コメントする

振り子の角度が小さいとき、また大きいときの振り子の取扱いです。
ラグランジアン\(L\)とハミルトニアン\(H\)から出発して運動方程式を求める方法を記述します。
座標は図のようにとります。
振り子のラグランジアンとハミルトニアン2
式で表せば、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
x&=r \sin{\theta} \\
y&=-r \cos{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
であり、1階微分は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\dot{x}&=\dot{r} \sin{\theta}+r\dot{\theta}\cos{\theta} \\
\dot{y}&=\dot{r} \cos{\theta} -r\dot{\theta}\sin{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
です。

[adsense1]

ラグランジアン\(L\)から出発

上の座標の元、デカルト座標\((x,y)\)での振り子のラグランジアン\(L(x,\dot{x},y,\dot{y},t)\)は
運動エネルギー\(K=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)\), ポテンシャルエネルギー\(V=V(x,\dot{x},y,\dot{y},t)\) より、
\(
\begin{align}
L(x,\dot{x},y,\dot{y},t)&=K-V \\
&=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)-V(x,\dot{x},y,\dot{y},t)
\end{align}
\)
と書けます。新たな座標系でのラグランジアン\(L(r,\dot{r},\theta,\dot{\theta},t)\)は\(\begin{eqnarray}
\left\{
\begin{aligned}
x&=r \sin{\theta} \\
y&=-r \cos{\theta}
\end{aligned}
\right.
\end{eqnarray}\)に従い座標変換をし、
\(
\displaystyle L(r,\dot{r},\theta,\dot{\theta},t)=\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r,\dot{r},\theta,\dot{\theta},t)
\)
とすることで新しい座標でのラグランジアンが得られます。
ここまでは一般的な話です。

今、もしも振り子をつないでいる棒が時間変化しない、言い換えれば束縛条件\(x^2+y^2=l^2\),(ここで\(l\)は定数)の元で考える場合、ポテンシャルエネルギーVは
\(
\begin{align}
V&=V(x,\dot{x},y,\dot{y},t)=-mgy \\
&=V(r,\dot{r},\theta,\dot{\theta},t)=mgr\cos\theta
\end{align}
\)
であり、\(\dot{l}=0\)なので
\(
\displaystyle L(\theta,\dot{\theta},t)=\frac{1}{2}ml^2\dot{\theta}^2-mgl\cos\theta
\)
となります。

運動方程式を求めるにはラグランジュの運動方程式
\(
\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta}=0
\)
に代入し、計算します。
\(
\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial \theta}&=0 \\
\frac{d}{dt}(ml^2\dot{\theta})+mgl\sin{\theta}&=0 \\
ml^2\ddot{\theta}&=-mgl\sin\theta \\
\ddot{\theta}&=-\frac{g}{l}\sin\theta
\end{align}
\)
となり\(\theta\)に関する微分方程式が導けました。

ハミルトニアン\(H\)から出発

ハミルトニアン\(H\)はラグランジアン\(L\)と一般化座標\(q_i\)と一般化運動量\(p_i\)を用いて、
\(
\displaystyle H(\vec{p},\vec{q},t)\equiv\sum_i p_i\dot{q}_i-L(\vec{q},\vec{\dot{q}},t)
\)
と定義されます。また、一般化運動量\(p_i\)は一般化座標\(q_i\)を用いて
\(
\displaystyle p_i=\frac{\partial L(q_i,\dot{q}_i,t)}{\partial \dot{q_i}}
\)
という関係で定義されます。

デカルト座標での一般化運動量\(p_x\)と\(p_y\)は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
p_x&=\frac{\partial L(x,\dot{x},y,\dot{y},t)}{\partial \dot{x}}=m\dot{x} \\
p_y&=\frac{\partial L(x,\dot{x},y,\dot{y},t)}{\partial \dot{y}}=m\dot{y}
\end{aligned}
\right.
\end{eqnarray}
\)
となるため、デカルト座標でのハミルトニアンは
\(
\begin{align}
H(x,p_x,y,p_y,t)&=p_x\dot{x}+p_y\dot{y}-\left\{\frac{1}{2}m(\dot{x}^2+\dot{y}^2)-V(x,\dot{x},y,\dot{y},t)\right\} \\
&=\frac{p_x^2}{m}+\frac{p_y^2}{m}-\left\{\frac{1}{2}m(\frac{p_x^2}{m^2}+\frac{p_y^2}{m^2})-V(x,\dot{x},y,\dot{y},t)\right\} \\
&=\frac{1}{2m}(p_x^2+p_y^2)+V(x,\dot{x},y,\dot{y},t)
\end{align}
\)
と求められます。

新たな座標系でのは一般化運動量\(p_r, p_{\theta}\)は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
p_r&=\frac{\partial L(r,\dot{r},\theta,\dot{\theta},t)}{\partial \dot{r}}=m\dot{r} \\
p_{\theta}&=\frac{\partial L(r,\dot{r},\theta,\dot{\theta},t)}{\partial \dot{\theta}}=mr^2\dot{\theta}
\end{aligned}
\right.
\end{eqnarray}
\)
なので、新たな座標系でのハミルトニアン\(H(r,p_r,\theta,p_{\theta},t)\)は
\(
\begin{align}
H(r,p_r,\theta,p_{\theta},t)&=p_r\dot{r}+p_{\theta}\dot{\theta}-\left\{\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2)-V(r,\dot{r},\theta,\dot{\theta},t) \right\} \\
&=\frac{p_r^2}{m}+\frac{p_{\theta}^2}{mr^2}-\left\{ \frac{p_r^2}{2m}+r^2\frac{p_{\theta}^2}{2mr^4} – V(r,\dot{r},\theta,\dot{\theta},t) \right\} \\
&=\frac{1}{2m}\left(p_r^2+\frac{p_{\theta}^2}{r^2}\right) + V(r,\dot{r},\theta,\dot{\theta},t)
\end{align}
\)
と求められます。

今、もしも振り子をつないでいる棒が時間変化しない、言い換えれば束縛条件\(x^2+y^2=l^2\), (ここで\(l\)は定数) の元で考える場合\(r=l\)を代入し、ポテンシャルエネルギー\(V\)は
\(
\begin{align}
V&=V(x,\dot{x},y,\dot{y},t)=-mgy \\
&=V(l,\dot{l},\theta,\dot{\theta},t)=mgl\cos\theta
\end{align}
\)
と求められます。今、\(p_l=m\dot{l}=0\)なのでハミルトニアンは
\(
\displaystyle H(\theta,p_{\theta},t)=\frac{p_{\theta}^2}{2ml^2}+mgl\cos{\theta}
\)
となります。
ハミルトンの正準運動方程式
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{\partial H}{\partial q_i}&=-\dot{p}_i \\
\frac{\partial H}{\partial p_i}&=\dot{q}_i
\end{aligned}
\right.
\end{eqnarray}
\)
に代入すれば
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{d p_{\theta}}{dt}&=-mgl\sin\theta \\
\frac{d \theta}{dt}&=\frac{p_{\theta}}{ml^2}
\end{aligned}
\right.
\end{eqnarray}
\)
より、\(p_{\theta}\)を消去すれば、
運動方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
と導けます。

振り子の運動方程式

今、解くべき方程式は
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
になります。

振り子の角度が小さいとき

まず、よく近似される角度が小さい時だけを議論するとします。
\(\sin\theta\)はテイラー展開より、
\(
\displaystyle \sin{\theta}= \theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots =\sum_{n=1}^{\infty}(-1)^{n+1}\frac{\theta^{2n-1}}{(2n-1)!}
\)
であるため、\(\theta\ll 1\)である場合は初めの1項だけ考慮し、
\(
\sin{\theta}\sim \theta
\)
と近似します。すると、
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta
\)
となります。

通常は解\(\theta(t)\)を\(C_1\sin(\sqrt{\frac{g}{l}}t)+C_2\cos(\sqrt{\frac{g}{l}}t)\)とか置いてしまいますが、今回は数学的な手順に従って導出します。

まず、\(\displaystyle\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}\)という量を計算すると、
\(
\displaystyle \frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=2\frac{d\theta}{dt}\cdot \frac{d^2\theta}{dt^2}
\)
という関係があることが分かります。これを利用すると2階微分を1階微分に落とすことができます。
まず、運動方程式の両辺に\(\displaystyle 2\frac{d\theta}{dt}\)を掛け、整理していきます。すなわち、
\(
\begin{align}
2\frac{d \theta}{dt}\cdot\frac{d^2 \theta}{dt^2}=-\frac{g}{l}2\frac{d \theta}{dt}\cdot\theta \\
\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=\frac{d}{dt}\left\{-\frac{g}{l}\theta^2\right\} \\
\left(\frac{d\theta}{dt}\right)^2=-\frac{g}{l}\theta^2+C_0
\end{align}
\)
となります。ここで\(\left(\frac{d\theta}{dt}\right)^2\)は\(\theta\)が虚数をとらない限り必ず正であることから、
\(-\pi\lt \theta\lt \pi\)の範囲で(ただし、\(\sin\theta\sim \theta\)の成り立つ近似の領域が\(\theta\)が小さい場合だけなので、まぁまぁ可能な範囲、として考えます。)
どんなに変化しても積分定数\(C_0\)はそれより大きい値(\(\left(\frac{d\theta}{dt}\right)^2\geq 0\)にする値、\(C_0\)は必ず正である。)でなければなりません。
それを考えながら左辺の2乗を取り払い、
\(
\begin{align}
\frac{d\theta}{dt} = \pm \sqrt{C_0-\frac{g}{l}\theta^2} \\
\pm \int \frac{1}{\sqrt{C_0-\frac{g}{l}\theta^2}}d\theta=\int dt
\end{align}
\)
となります。左辺を計算するため変数変換
\(
\displaystyle \sqrt{\frac{g}{l}}\theta=\sqrt{C_0}\sin\phi
\)
を行います。
\(
\displaystyle \frac{d \theta}{d\phi}=\sqrt{\frac{l}{g}C_0}\cos\phi
\)
なので
\(
\begin{align}
\displaystyle \int \frac{1}{\sqrt{C_0-\frac{g}{l}\theta^2}}d\theta
&=\displaystyle \int \frac{1}{\sqrt{C_0}\sqrt{1-\sin^2{\phi}}}\cdot\sqrt{\frac{l}{g}C_0}\cos{\phi}d\phi \\
&=\sqrt{\frac{l}{g}}\phi \\
&=\sqrt{\frac{l}{g}}\sin^{-1}\left(\sqrt{\frac{g}{lC_0}}\theta\right)
\end{align}
\)
と計算できるので、
\(
\begin{align}
\sqrt{\frac{l}{g}}\sin^{-1}\left(\sqrt{\frac{g}{lC_0}}\theta\right)=t+C_1 \\
\theta(t)=\sqrt{\frac{l}{g}C_0}\sin\left(\pm \sqrt{\frac{g}{l}}(t+C_1)\right)
\end{align}
\)
と書けます。\(C_0,C_1\)は単なる積分定数であるためにそれ自体の意味はなく、また、\(\sin\)の中の±は\(C_1\)を調節すれば関係なくなるので、それらを省略すれば
\(
\displaystyle \theta(t)=C_0\sin\left(\sqrt{\frac{g}{l}}t+C_1\right)
\)
となります。角周波数は
\(\displaystyle \omega=\sqrt{\frac{g}{l}}\)
となります。

角度が小さいときはこれでお仕舞いにします。

振り子の角度が大きいとき

楕円関数というものが計算を行っていくと出てきます。そこに至るまでの手順は振り子の角度が小さいときの手順に途中まで同じです。
対象になる問題は
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta
\)
です。ここで\(\sqrt{\frac{g}{l}}=\omega\)とおいて、
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\omega^2\sin\theta
\)
と書き直します。
振り子の角度が小さいときと同じようにまず２階微分を１階微分に焼直すため、両辺に\(\displaystyle 2\frac{d\theta}{dt}\)を掛けて、
\(
\begin{align}
2\frac{d \theta}{dt}\cdot\frac{d^2 \theta}{dt^2}=-\omega^2\frac{d \theta}{dt}\cdot \sin\theta \\
\frac{d}{dt}\left\{\left(\frac{d\theta}{dt}\right)^2\right\}=\frac{d}{dt}\left\{2\omega^2\cos\theta\right\} \\
\left(\frac{d\theta}{dt}\right)^2=2\omega^2\cos(\theta)+C_0
\end{align}
\)
ここで左辺はゼロ以下になることはないため、そうなるように積分定数\(C_0\)を決めます。
ここでの積分定数\(C_0\)の持つ物理的な意味をちょっと考えます。
振り子には大きく分けて２種類の運動が存在します。１つは\(\theta\)が小さいときの運動の延長線上にある、最下点を中心として振動する運動であり、もう1つはぐるんぐるん回る運動です。
ちょっと違う言い方をすれば、1つ目の運動は必ず粒子の速度の大きさ\(|v|=l|\frac{d \theta}{dt}|\)=0になる時間が存在する運動を表し、2つ目の運動は常に速度の大きさ\(|v|\)がゼロではない有限の値を持つ運動を表します。
この運動の区別がこの積分定数\(C_0\)に依存するのです。

何はともあれ、数学的な話をしていけば２つの運動を記述する微分方程式はどちらも\(\displaystyle \frac{d^2\theta}{dt^2}=-\omega^2\sin\theta\)であるので、これが解ければ自然と両方の運動を記述する答えが得られるはずです。その区別は後で考えましょう。

つまり、言いたかったことは\(C_0\)はいつも\(2\omega^2\cos(\theta)\)以上ですよ、ということを言いたかったんです。
よって、左辺のルートを取り払います。
\(
\begin{align}
\left(\frac{d\theta}{dt}\right)^2 &=2\omega^2\cos(\theta)+C_0 \\
\frac{d\theta}{dt} &=\pm\sqrt{C_0+2\omega^2\cos(\theta)}
\end{align}
\)
天下り的ですが、ここで
\(
\displaystyle \cos\theta=1-2\sin^2{\frac{\theta}{2}}
\)
の関係式を使って、
\(
\begin{align}
\frac{d\theta}{dt} &=\pm\sqrt{C_0+2\omega^2\left(1-2\sin^2{\frac{\theta}{2}}\right)} \\
&=\pm \sqrt{(C_0+2\omega^2)}\sqrt{1-\frac{4\omega^2}{C_0+2\omega^2}\sin^2\frac{\theta}{2}} \\
&=\pm 2\omega k\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}
\end{align}
\)
となります。ここで\(\displaystyle \frac{1}{k}=\sqrt{\frac{4\omega^2}{C_0+2\omega^2}}\)という量\(k\)を定義しました。
なぜ\(\frac{1}{k}\)なの？という理由は後々都合がよくなるからです。深い意味はありません。

運動方程式は
\(
\begin{align}
\frac{d\theta}{dt}=\pm 2\omega k\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}
\end{align}
\)
とここまで簡略化されました。積分します。
\(
\displaystyle \pm\frac{1}{2\omega k}\int_{\theta_0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta=\int_{t_0}^{t} dt
\)
となります。積分区間は初期時刻\(t_0\)に角度\(\theta_0\)にいた質点が時刻\(t\)には角度\(\theta\)にいることを意味します。
通常、積分区間は積分定数\(C_1\)を使って表します。この積分区間は以下の変形が可能です。丁寧にやると、
\(
\begin{align}
\int_{\theta_0}^{\theta} f(\theta)d\theta &= \int_{t_0}^{t} g(t) dt \\
\int_{\theta_0}^{0} f(\theta)d\theta+\int_{0}^{\theta} f(\theta)d\theta &= \int_{t_0}^{0} g(t) dt+\int_{0}^{t} g(t) dt \\
\int_{0}^{\theta} f(\theta)d\theta &= \int_{0}^{t} g(t) dt + C_1
\end{align}
\)
です。よって
\(
\displaystyle \pm\frac{1}{2\omega k}\int_{0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta=\int_{0}^{t} dt + C_1
\)
を解けば良いことになります。左辺の積分を解きましょう。
変数変換\(\frac{1}{k}\sin\frac{\theta}{2}=\sin{\phi}\)を行います。

\(
\begin{align}
\frac{d}{d\phi}\left(\frac{1}{k}\sin\frac{\theta}{2}\right)&=\frac{d}{d\phi}\sin\phi \\
\frac{1}{k}\cos\left(\frac{\theta}{2}\right)\frac{1}{2}\frac{d \theta}{d\phi} &= \cos\phi \\
\frac{d \theta}{d\phi} &= 2k \frac{\cos{\phi}}{\cos\frac{\theta}{2}}
\end{align}
\)
となります。積分区間は
\(
\begin{align}
&\theta\ \ | 0 \rightarrow \ \theta \\
&\phi\ \ | 0 \rightarrow \ \phi(=\sin^{-1}(\frac{1}{k}\sin{\frac{\theta}{2}})) \\
\end{align}
\)
と変化します。左辺に代入すれば、
\(
\begin{align}
\pm\frac{1}{2\omega k}\int_{0}^{\theta} \frac{1}{\sqrt{1-\frac{1}{k^2}\sin^2\frac{\theta}{2}}}d\theta
&=\pm\frac{1}{2\omega k}\int_{0}^{\phi} \frac{1}{\sqrt{1-\sin^2\phi}}2k\frac{\cos{\phi}}{\cos\frac{\theta}{2}} d\phi \\
&=\pm \frac{1}{\omega} \int_{0}^{\phi} \frac{1}{\cos\frac{\theta}{2}}d\phi \\
&=\pm \frac{1}{\omega} \int_{0}^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi \\
\end{align}
\)
となります。故に、
\(
\displaystyle \int_{0}^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi =\pm\omega t+C_1
\)    …(A)
と表されます。左辺の積分は楕円積分と呼ばれています。

第一種Legendre楕円積分は
\(
\displaystyle F(\phi, k)=\int_0^{\phi} \frac{1}{\sqrt{1-k^2\sin^2\phi}}d\phi
\)
と定義されます。この逆関数の\(sin\)はJacobiの楕円関数\(sn(u,k)\)をして定義されています。
どういうことかといえば、\(u=F(\phi, k)\)のとき、\(\phi=F^{-1}(u,k)\)であるので、
\(
\sin\phi=\sin(F^{-1}(u,k))=sn(u,k)
\)
という関数を定義するのです。

すると、今、\(\pm \omega t+C_1=F(\phi, k)\)であるため、
\(
\begin{align}
\pm \omega t+C_1&=F(\phi, k)=u \\
\phi&=F^{-1}(\pm \omega t+C_1, k) \\
\sin\phi &=\sin(F^{-1}(u,k)) \\
\sin\phi &=sn(u,k)
\end{align}
\)
となります。

\(\sin\phi=\frac{1}{k}\sin\frac{\theta}{2}\)なので求めたかった\(\theta(t)\)は
\(
\begin{align}
\sin{\frac{\theta}{2}}=k\ sn(\pm\omega t+C_1, k) \\
\theta(t)=2\sin^{-1}(k\ sn(\pm\omega t+C_1, k))
\end{align}
\)
と求められます。

[adsense2]

Jacobiの楕円関数は数値計算的にはランデンの方法という方法で計算されるそうです。
さて、式(A)を見ていると、kが1以上の場合、なんかおかしいことに気が付くかと思います。もしもkが1以上の場合、被積分関数のルートの中が負になることがあり得るんじゃ・・・？
実はこの状況が生まれることはありません。これは積分範囲が今\(0\sim\phi\)になっていますが、\(\phi=\sin^{-1}(\frac{1}{k}\sin{\frac{\theta}{2}})\)であらわされる区間なので、kの値に応じてとりうる積分範囲は必ずルートの中が負にならない範囲に収まるのです。

ただ、上の問題を心配する必要が無いようにkの範囲は\(0\le k\le 1\)に通常は制限されます。
k=2の楕円関数は存在するのに範囲が制限されて、計算どうするの？という疑問が生まれます。
これを解決するのはJacobiの楕円関数snの性質を利用します。
Jacobiの楕円関数は三角関数の拡張であるとみなせるので、その性質は非常に多岐にわたります。
その中の一つにこういう関係式があります。
\(
\displaystyle sn(u,\frac{1}{k})=k\ sn(\frac{u}{k},k)
\)
これを使うとkが1より大きい時でも変換することができます。

具体的には、
\(
\begin{eqnarray}
\theta(t)=
\left\{
\begin{aligned}
& 2\sin^{-1}(k\ sn(\pm\omega t+C_1, k)) \dots (0 \lt k \lt 1) \\
& 2\sin^{-1}(sn(k \omega t+C_1),\frac{1}{k}) \dots (1\lt k)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。運動の状態と対応させるのであれば、一つ目の式\((k\lt 1)\)の場合は往復運動をし、\((k\gt 1)\)の時はぐるんぐるん回る運動に対応します。

１往復、または１回転に要する時間Tは
\(
\begin{eqnarray}
T=
\left\{
\begin{aligned}
&\frac{4}{\omega}K(k) \dots (0 \lt k \lt 1) \\
&\frac{2}{k\omega}K(\frac{1}{k}) \dots (1 \lt k1)
\end{aligned}
\right.
\end{eqnarray}
\)
として与えられます。ここでK(k)は第1種完全楕円積分で、
\(
\displaystyle K(k)=\int_0^1 \frac{1}{\sqrt{(1-x^2)(1-k^2 x^2)}}dx
\)
という定積分です。

※
例えば、微分方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\sin\theta
\)
を
\(
t=0,\; \theta=0; \frac{d\theta}{dt}=1.9 (k=0.95)
\)
の初期条件の下解いた場合、
1周期\(T\)は
\(
T=4K(0.95)=10.360044923498004876778\cdots
\)
となります。
この値はwolfram alphaから求めました。
4*EllipticK[0.95*0.95] wolfram alpha
wolfram alphaでの第1種完全楕円積分は
\(
\displaystyle EllipticK[k’]=\int_0^1 \frac{1}{\sqrt{(1-x^2)(1-k’ x^2)}}dx
\)
として定義されているので注意が必要です。


参考文献

森口繁一, 宇田川銈久, 一松信著『数学公式Ⅲ 特殊関数』岩波書店(1960)p.40~45
Hamilton の正準運動方程式 -epii’s physics notes
KIT -数学ナビゲーション
振り子と楕円関数
Jacobi Elliptic Functions — from Wolfram MathWorld