amesyabody のすべての投稿

数学, 物理学

縮約

コメントする

縮約はアインシュタインが一般相対性理論を説明するために最初に導入した数式のお約束です。
これが考え出されたのはアインシュタインが

和記号を書くのに飽きた

からであると予想されます。
このお約束なんですが，大学の物理科ではあまり触れられない癖に教授たちは常識のように語るので，
身につけておいて損はないですね。

さて，あるテンソル量\(A_{i}\)と\(B_{i}\)があったとしましょう。
この二つの縮約をとるということは，同じテンソル同士の和を取る，という意味になります。
アインシュタインの記法に則れば次のように書きます。

\(
A_{i}B^{i}=\sum_{i}{A_{i}B_{i}}
\)

ようするに同じ添え字が右下と右上に来たら和をとりましょうという約束です。
上の式は内積を表していることがわかります。
これを使うと外積の\(i\)成分も次のようになります。

\(
(A \times B)_i= \epsilon_{i,j,k}A^{j}B^{k}
\)
\(
\epsilon_{i,j,k}= 1 ~~ {\rm at} ~~ i,j,k=(1,2,3),(2,3,1),(3,1,2)
\)
\(
\epsilon_{i,j,k}= -1 ~~ {\rm at} ~~ i,j,k=(1,3,2),(3,2,1),(2,1,3)
\)
\(
\epsilon_{i,j,k}= 0 ~~ {\rm at} ~~ i,j,k=(otherwise)
\)

この\(\epsilon_{i,j,k}\)をレヴィチビタの完全反対称テンソルといいます。

プログラミングと数値計算, 物理学

モンテカルロ法

2件のコメント

モンテカルロ法は，乱数を使って系の平衡状態にせまる一つの方法です。

ここでは二次元正方格子のイジング模型について紹介します。
イジング模型は隣り合う格子のスピン同士の相関エネルギーのみを考慮した模型です。
ハミルトニアンは以下のようになります。

\(
\displaystyle
H=-J \Sigma_{< i , j >}{s_{i}s_{j}}
\)
　
あるスピン状態を持つ系の状態Aについて，そのハミルトニアンを\(H_A\)とすると，
ボルツマン因子と分配関数\(Z\)を用いて状態の実現確率を計算することが出来ます。

\(
P(A)=\frac{\exp{(-\frac{H_A}{k_B T})}}{Z}
\)
　
Aからランダムに一つの格子におけるスピンを一つだけフリップした状態を状態Bとして，
状態Aと状態Bの実現確率比を乱数と比較します。
\(P(B)/P(A)>{\rm random}\)ならば状態Bを採用し，そうでなければ状態Aを採用します。
ここまでの流れを1mcs(モンテカルロステップ)といい，これを何度も繰り返すことで平衡状態に近づきます。
以下の二つのgifは，相転移温度より高い温度と低い温度で，
モンテカルロステップにより二次元正方格子のスピンがどのように振る舞うかをみているアニメーションです。
黒がダウンスピン，白がアップスピンです。


温度T=10eVのスピンの挙動
温度T=10eVのスピンの挙動

こちらは温度T=10eVで，自発磁化を持たない事が分かります。


温度T=0.001eVのスピンの挙動
温度T=0.001eVのスピンの挙動

こちらは温度T=0.001eVで，スピンが揃って自発磁化を持つ事が分かります。

画像をクリックするとmcsスタート!!

スピンのふるまいを追うと，自発磁化を持つ温度と持たない温度でスピンのふるまいが違う事が分かります。
二次元のイジング模型はオンサーガーにより厳密に解かれている(相転移温度T=2.26eV at J=1)ので，
それを踏まえて下のプログラムで遊んでみるといいですよ。

これのプログラムソースコード(保証は一切しません!!)
*注意　このプログラムを実行する前にising_anというディレクトリを作ってください。
*追記　2015 2/13　磁化とエネルギーを計算出来るようにしました。
計算方法は重み付き選択法というのを使ってます。

\(
\langle A \rangle = \frac{1}{T} \sum_{t=t_0+1}^{t_0 + T}A_{\alpha_{t}}
\)
　
十分平衡状態になっている\(t_0\)以降のモンテカルロステップで，物理量の統計平均を取る方法です。
平衡以前の物理量を計算しないmcsをからまわしと言います。

格子点51×51で，\(J=2\)で計算しました。
スピンの大きさを1として，相互作用をダブルカウントしているので注意しましょう。
即ち\(J=1\)の結果が欲しければプログラム上ではintJ=0.125にすればよいかも。

**********parameter**********
i_max::x方向の格子点の数
j_max::y方向の格子点の数
mcs_max::最大モンテカルロステップ数
mcs2step::mcs2step以降のmcsを平衡状態と見なし，物理量を計算します
intj::\(J/4\)
temp::温度
mov_max::mcs_max/movmax毎のスピン状態をgifアニメーションで見れるように区切ります。
**********parameter**********

単位格子あたりのエネルギーの温度依存性グラフを添付します。

ene

相転移温度付近でエネルギーの変化が大きい事が分かります。

単位格子あたりの磁化の絶対値の温度依存性グラフを添付します。

mag

相転移温度付近で自発磁化が発生し始めている事が分かります。

gnuplotを用いて，格子点上のスピンがどのように平衡状態へ近づくかをダイナミックに確認する事が出来ます。

gnuplot anime.gnuplot
　
を実行するとアニメが始まります。

gnuplot animegif.gnuplot
　
でgifアニメが作成出来ます。

!————————————————
! title = ising2d.f90
! developer = Amesyabody
! released = 2015 2/13
! programming language = fortran
!
!explanation
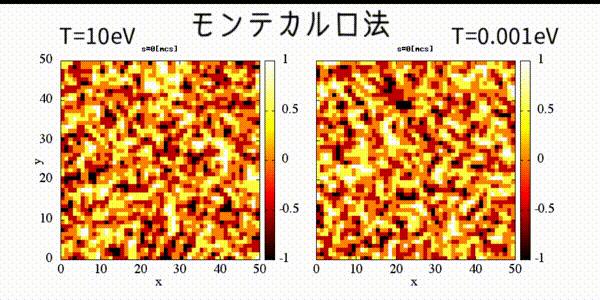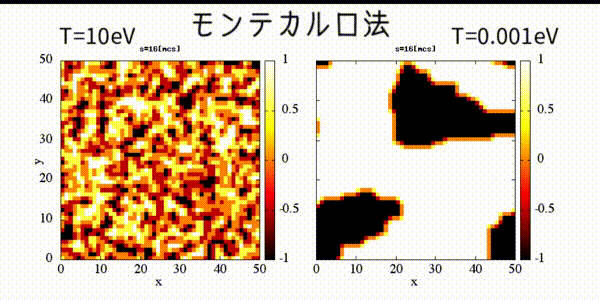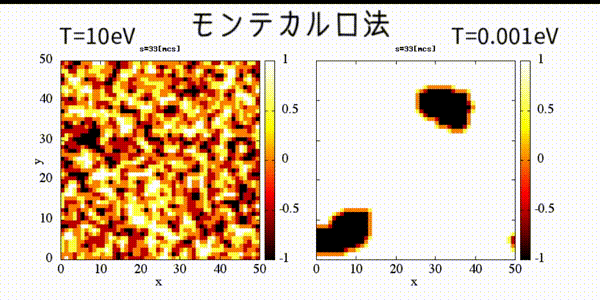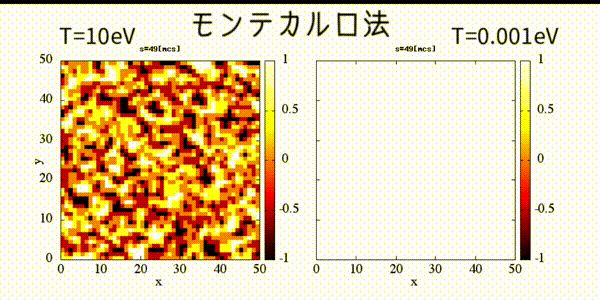
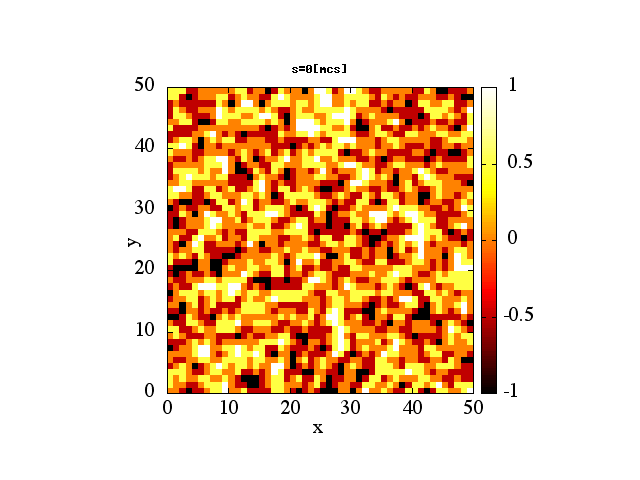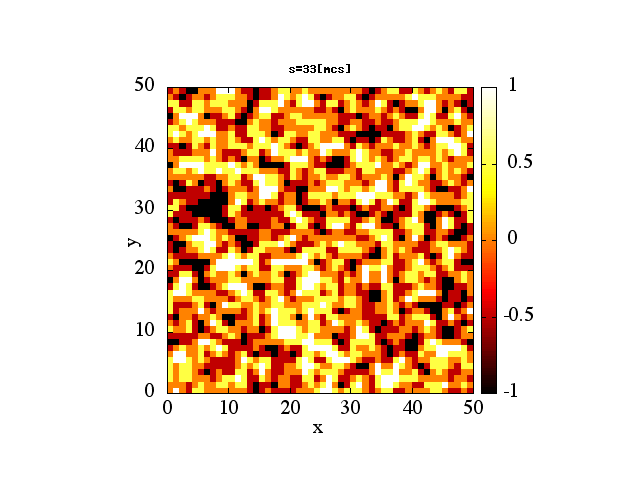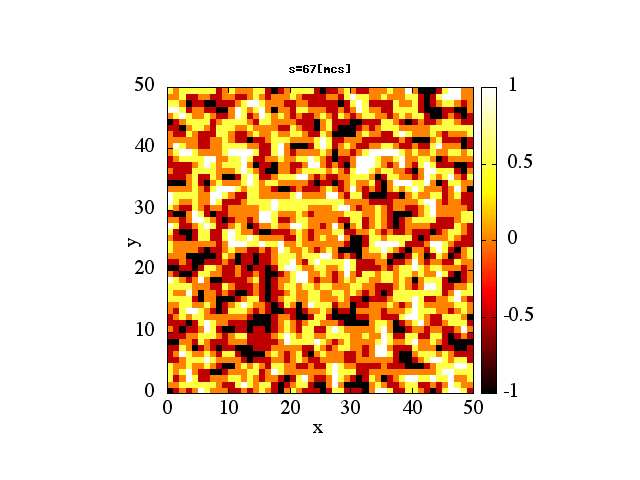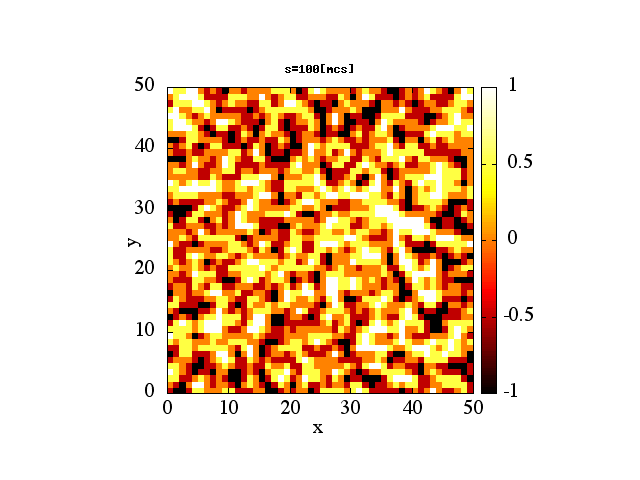
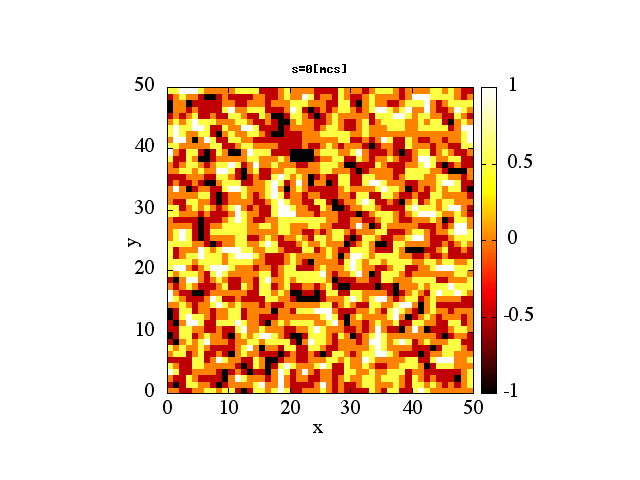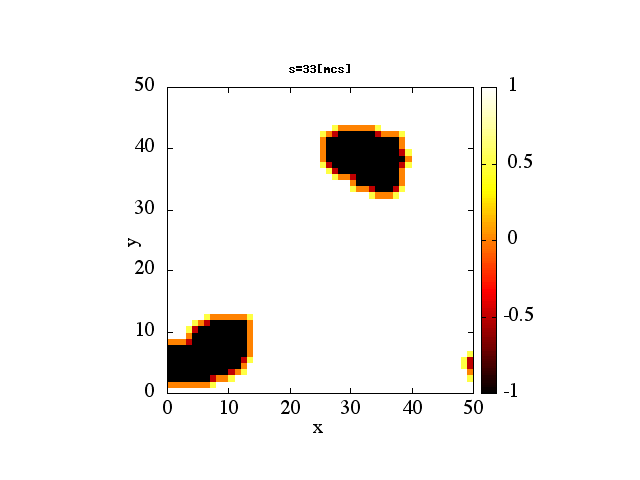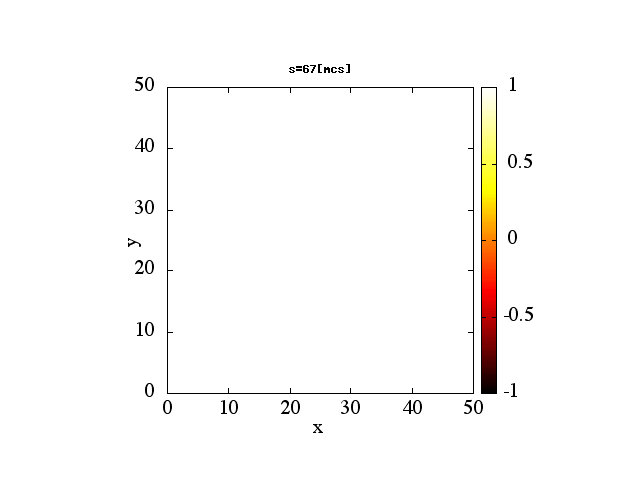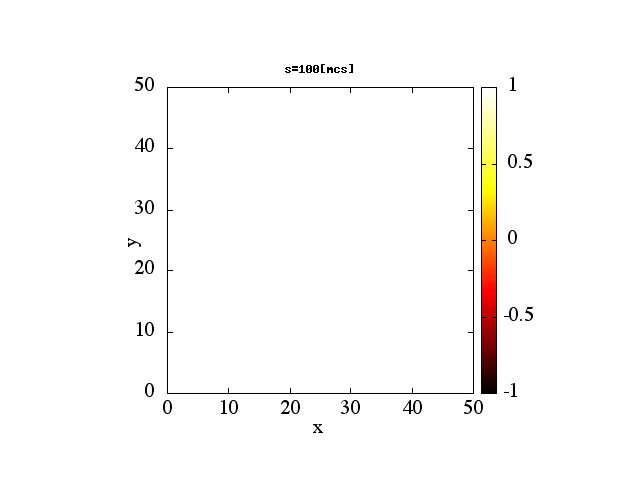
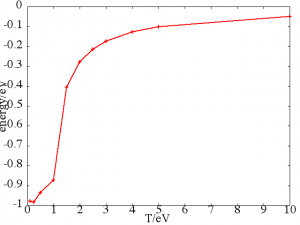
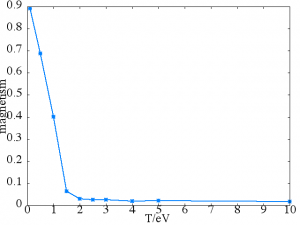
!2 dimentional square lattice Ising model's dynamical magnetism
!calculated by Monte Carlo method.
!————————————————
   
program main
    implicit none
    integer(4)::i,j,i_max,j_max,mcs,mcs_max,mov,mov_max,mcs2step
    parameter(i_max=50,j_max=50,mcs_max=1000000,&
    mcs2step=500000,mov_max=100)
    real(8)::intj,temp
    parameter(intj=0.25d0,temp=0.1d0)
    real(8)::spin(0:i_max,0:j_max)
    real(8)::ratio,ham1,ham2,hamres,dum,ene
    integer(4)::px,mx,py,my,rndx,rndy
    character(10)::movc,movc2

    real(8)::mag,mag2,magres
   
    !-----make random-----
    integer(4),allocatable::seed(:)
    integer cnt,seedsize
    real(8)::rnd,rndi,rndj,rnds
   
    call random_seed(size=seedsize)
    allocate(seed(seedsize))
    write(*,*)seedsize

    dum=rndmf(0)

    call system_clock(count=cnt)
    seed=cnt!+idnint(dum*1000000)
!            dum=rndmf(seed(0))
!            seed=idnint(seed*dum)
    call random_seed(put=seed)

    !------------------

mag2=0.0d0
ene=0.0d0

do mov=0,mov_max

write(movc,'(i3)')mov

open(100+mov,file="ising_an/spin"//trim(adjustl(movc))//".dat"&
,status="unknown")

end do

open(5000,file="ising_an/anime.gnuplot",status="unknown")
open(5001,file="ising_an/animegif.gnuplot",status="unknown")

    !-----primitive spin set-----
   
    do i=0,i_max
        do j=0,j_max
            call random_number(rnd)
!           write(*,*)rnd
            if(rnd>0.5d0)then
                spin(i,j)=1.0d0
            else
                spin(i,j)=-1.0d0
            end if
!           write(*,*)spin(i,j)!,cnt,seed(1)

        write(100,'(i3,i3,f5.1)')i,j,spin(i,j)

        end do

        write(100,*)" "

    end do
   
    !----------------------------
   
    do mcs=1,mcs_max
   
        do i=0,i_max
       
            do j=0,j_max
           
                px=i+1
                if(i==i_max)px=px-i_max-1
                py=j+1
                if(j==j_max)py=py-j_max-1
                mx=i-1
                if(i==0)mx=mx+i_max+1
                my=j-1
                if(j==0)my=my+j_max+1

                ham1=ham1-intj*spin(i,j)*spin(px,j)&
                -intj*spin(i,j)*spin(i,py)&
                -intj*spin(mx,j)*spin(i,j)&
                -intj*spin(i,my)*spin(i,j)

                do mov=1,mov_max-1

                    if(mcs==mov*mcs_max/mov_max)&
                    write(100+mov,'(i3,i3,f5.1)')i,j,spin(i,j)

                end do

                if(mcs>mcs2step)then

                    mag2=mag2+spin(i,j)

                end if
               
            end do

            do mov=1,mov_max-1

                if(mcs==mov*mcs_max/mov_max)write(100+mov,*)" "

            end do

        end do

        if(mcs>mcs2step)then

            magres=magres+abs(mag2)
            mag2=0.0d0
            ene=ene+ham1

        end if

        call random_number(rndi)
        call random_number(rndj)
        rndx=idnint(rndi*i_max)
        rndy=idnint(rndj*j_max)

!       write(*,*)rnd
!write(*,*)spin(rndx,rndy)
        spin(rndx,rndy)=-spin(rndx,rndy)
!write(*,*)spin(rndx,rndy)
        do i=0,i_max
       
            do j=0,j_max
           
                px=i+1
                if(i==i_max)px=px-i_max-1
                py=j+1
                if(j==j_max)py=py-j_max-1

                mx=i-1
                if(i==0)mx=mx+i_max+1
                my=j-1
                if(j==0)my=my+j_max+1

                ham2=ham2-intj*spin(i,j)*spin(px,j)&
                -intj*spin(i,j)*spin(i,py)&
                -intj*spin(mx,j)*spin(i,j)&
                -intj*spin(i,my)*spin(i,j)
   
            end do
           
        end do
       
        ratio=exp((-ham2+ham1)/temp)
!       write(*,*)ham1,ham2,ratio
       
        ham1=0.0d0
        ham2=0.0d0
       
        call random_number(rnds)

        if(ham1 > ham2)then!metroporis
        goto 200
        end if
       
        if(rnds>ratio)then
        spin(rndx,rndy)=-spin(rndx,rndy)
        end if

200     continue

    end do
   
    do i=0,i_max
        do j=0,j_max
       
        mag=mag+spin(i,j)
       
        px=i+1
        if(i==i_max)px=px-i_max-1
        py=j+1
        if(j==j_max)py=py-j_max-1
        mx=i-1
        if(i==0)mx=mx+i_max+1
        my=j-1
        if(j==0)my=my+j_max+1

        hamres=hamres-intj*spin(i,j)*spin(px,j)&
        -intj*spin(i,j)*spin(i,py)&
        -intj*spin(mx,j)*spin(i,j)&
        -intj*spin(i,my)*spin(i,j)

        write(100+mov_max,'(i3,i3,f5.1)')i,j,spin(i,j)
       
        end do

        write(100+mov_max,*)" "

    end do
   
    mag=mag/(dble(i_max*j_max))
   
!   write(*,'(3f10.5,f15.5)')temp,intj,mag,hamres

    ene=ene/(dble((mcs_max-mcs2step)*(i_max+1)*(j_max+1)))
    magres=magres/(dble((mcs_max-mcs2step)*(i_max+1)*(j_max+1)))

    write(*,'(A,f10.5,A,f10.5)')"energy=",ene,"      magnet=",magres

    write(5000,*)"set size sq"
    write(5000,*)"set pm3d map"
    write(5000,*)"set palette rgbformulae 21,22,23"
    write(5000,*)"set xlabel 'x'"
    write(5000,*)"set ylabel 'y'"
    write(5000,*)"set zra[-1:1]"
    write(5000,*)"set zlabel 'spin'"
    write(5000,*)"splot 'spin0.dat'"
    write(5000,*)"pause 0.1"
    do mov=1,mov_max
    write(movc,'(i3)')mov
    write(5000,*)"splot 'spin"//trim(adjustl(movc))//".dat'"
    write(5000,*)"pause 0.1"

    end do

    write(5001,*)"set tics font 'Times,15'"
    write(5001,*)"set xlabel font 'Times,15'"
    write(5001,*)"set ylabel font 'Times,15'"
    write(5001,*)"set size sq"
    write(5001,*)"set pm3d map"
    write(5001,*)"set palette rgbformulae 21,22,23"
    write(5001,*)"set xlabel 'x'"
    write(5001,*)"set ylabel 'y'"
    write(5001,*)"set zra[-1:1]"
    write(5001,*)"set cbrange [-1:1]"
    write(5001,*)"set zlabel 'spin'"
    write(5001,*)"set term gif animate optimize"
    write(5001,*)"set output 'is_t10.gif'"
    write(5001,*)"do for[i=0:100] {"
    write(5001,*)'file = sprintf("spin%01d.dat", i)'
    write(movc2,'(i10)')mcs_max/mov_max
    write(5001,*)'time = sprintf("s=%d[mcs]",i*'//trim(adjustl(movc2))//')'
    write(5001,*)"set title time"
    write(5001,*)"splot file"
    write(5001,*)"}"

    contains

real(8) function rndmf(seeds)
implicit none

integer(4)::a,m,q,p,n,ndiv,j,k,seeds
real(8)::rm,rmax
parameter(a=16807,m=2147483647,rm=1.0/m)
parameter(q=127773,p=2836,n=32,ndiv=1+(m-1)/n)
parameter(rmax=1.0-1.2e-7)
integer(4)r(n),r0,r1

if (seeds .ne. 0)then
r1=abs(seeds)
do j=n+8,1,-1
k=r1/q
r1=a*(r1-k*q)-p*k
if(r1 .lt. 0)r1=r1+m
if(j .le. n)r(j)=r1
end do
r0=r(1)
end if


k=r1/q
r1=a*(r1-k*q) -p*k
if(r1 .lt. 0)r1=r1+m
j=1+r0/ndiv
r0=r(j)
r(j)=r1
rndmf=min(rm*r0,rmax)

end function
   
end program