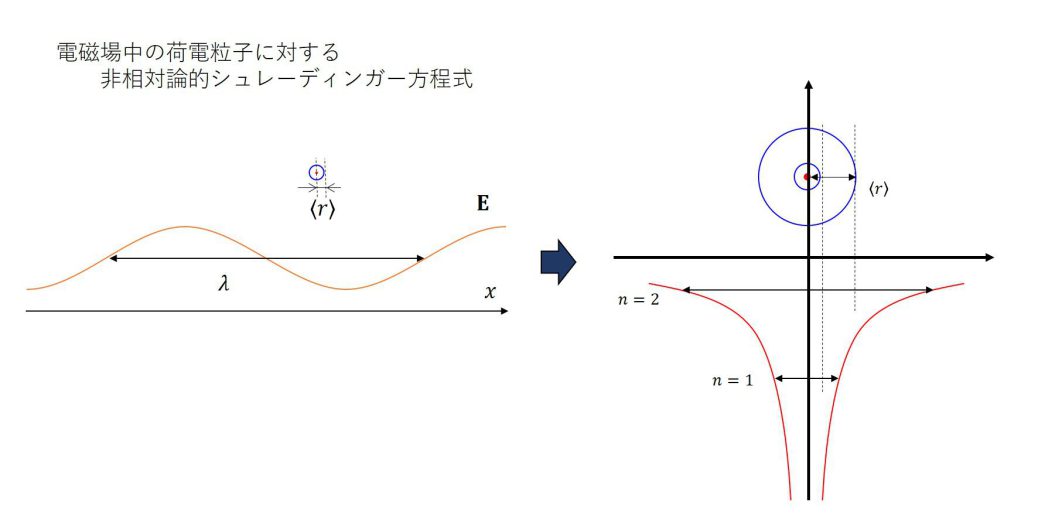
本稿では電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式から双極子近似についてまで説明を行います.

ここでは目的と結論しか載せませんので、詳しくは以下のPDFをご覧ください。
https://slpr.sakura.ne.jp/qp/supplement_data/nrtdse_in_electromagneticfields/oneElectronAtom_electricField.pdf

目的と結論

---

自由粒子に対する非相対論的シュレーディンガー方程式

からスタートして, 電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式

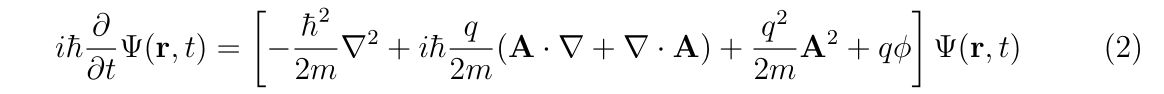
を導きます\((\mathbf{A}=\mathbf{A}(\mathbf{r},t), \phi=\phi(\mathbf{r},t))\).

その後, クーロンゲージ\((\nabla\cdot \mathbf{A}=0)\)を満たす\(\chi(\mathbf{r},t)\)を選び, かつ双極子近似\((\mathbf{A}\approx\mathbf{A}(t))\)を採用した場合に電磁場中の一電子原子の電子(電荷\(q=-e\))に対する, 速度ゲージ (Velocity gauge) , 長さゲージ (Length gauge) における真空中の非相対論的シュレーディンガー方程式

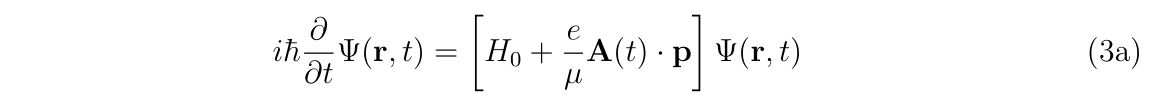
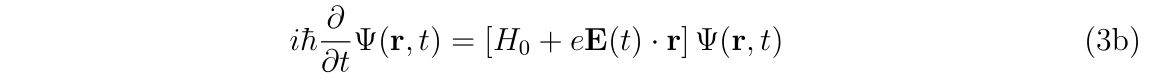
を導きます.ここで\(H_0\)は電磁場のない空間における原子のポテンシャルです. 式(3a)は速度ゲージ, 式(3b)は長さゲージにおける非相対論的シュレーディンガー方程式と呼ばれています. 双極子近似である式(3a), (3b)は, \(\mathbf{A}^2\)を含む非線形項を無視するので, 一光子過程しか考えない( 多光子過程が起こらない)という近似が入っています.

本稿の主な参考文献は,
B. H. Bransden and C. J. Joachain, 2003, “Physics of Atoms and Molecules second edition” , Prentice Hall, ISBN 0-582-35692-X
の第4章”Interaction of one-electron atoms with electromagnetic radiation”を元にしていますので, 正確な文章を希望する方はこちらをご参照ください.