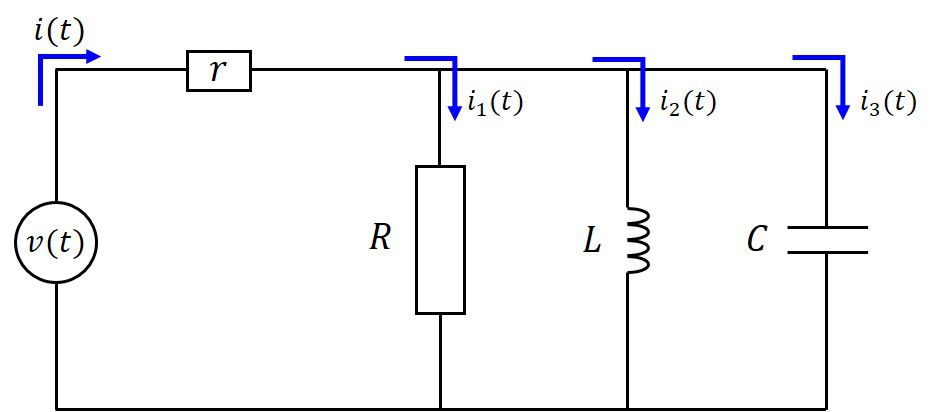
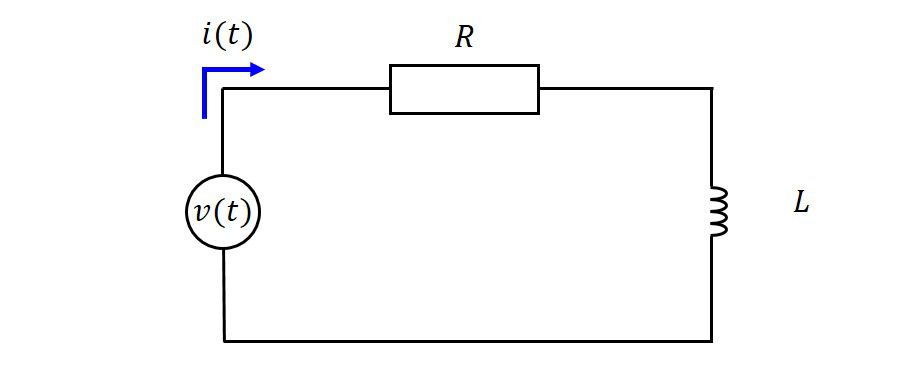
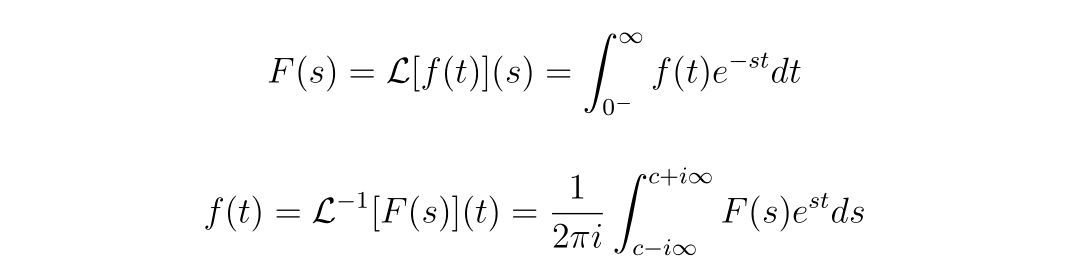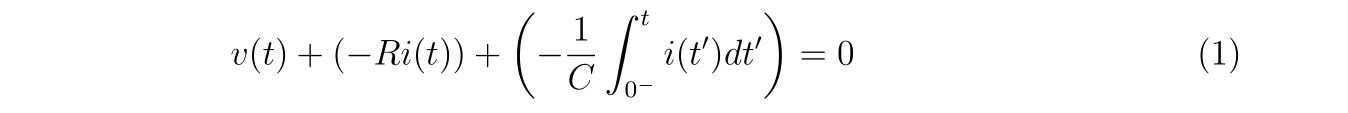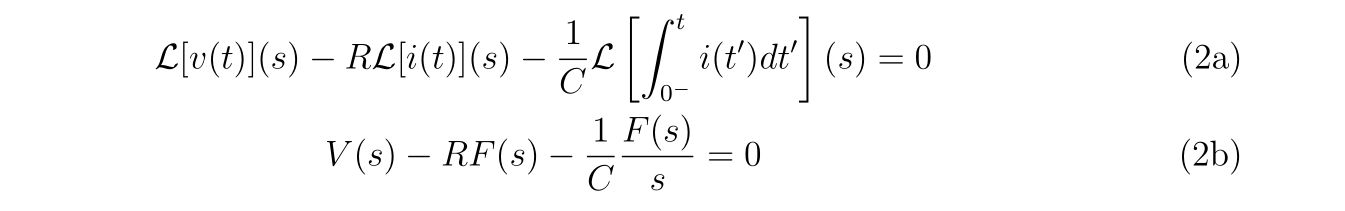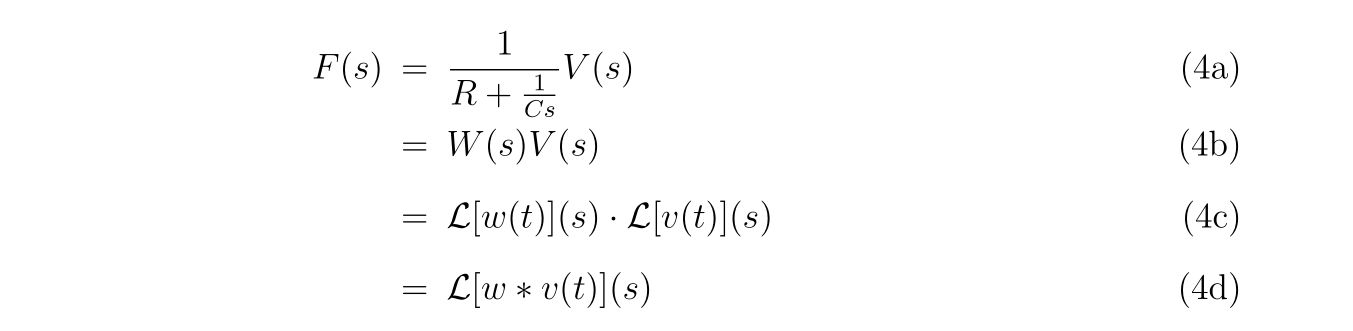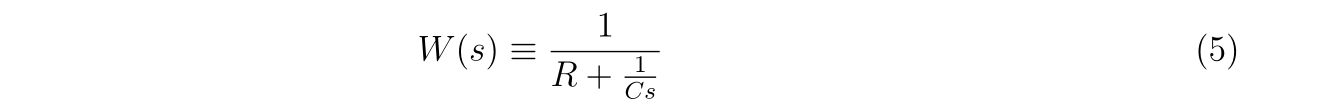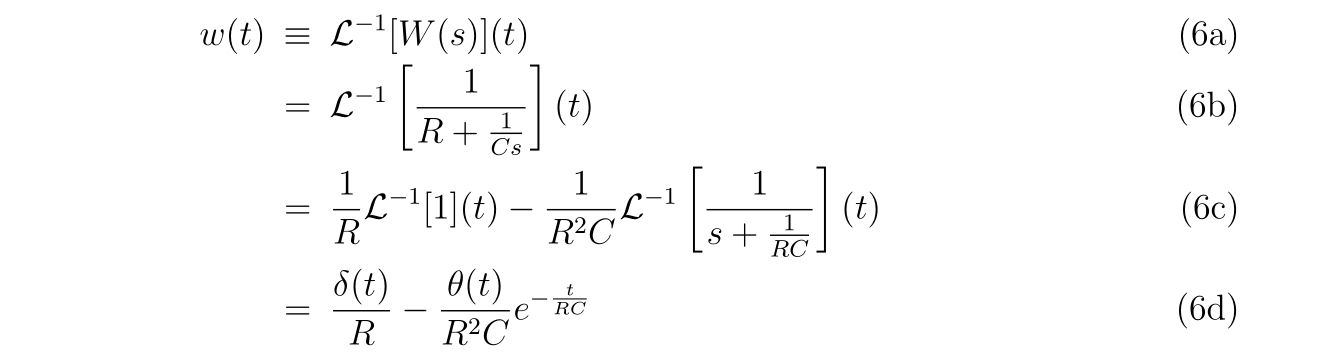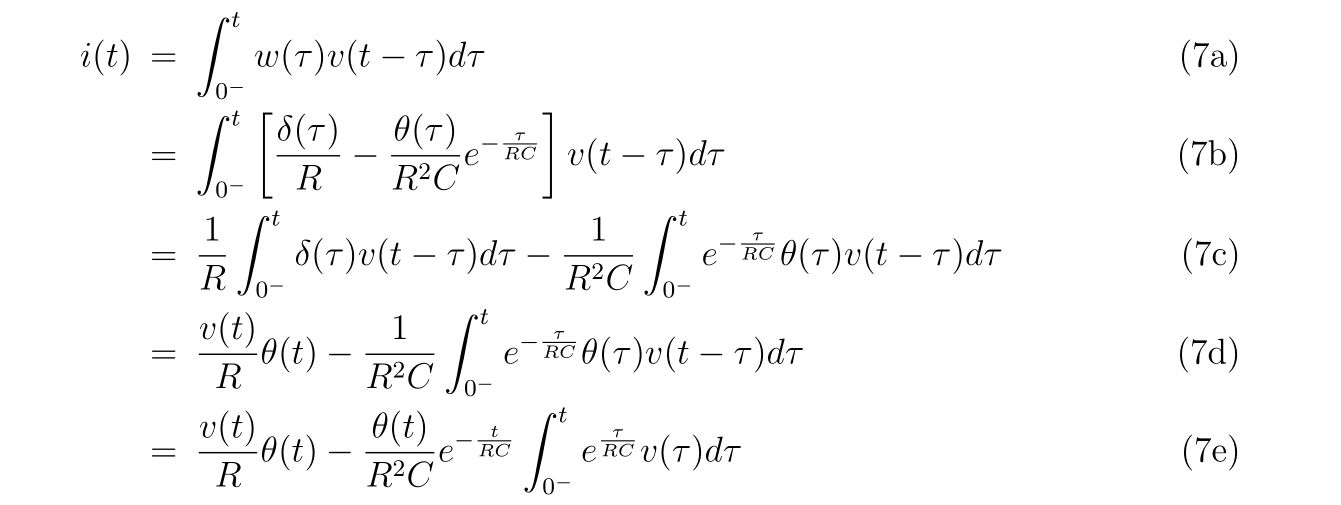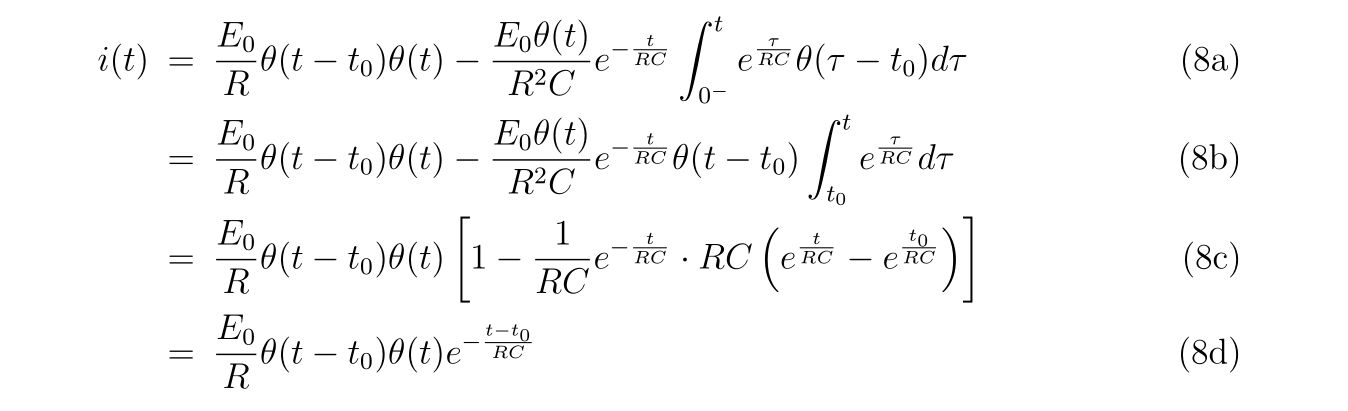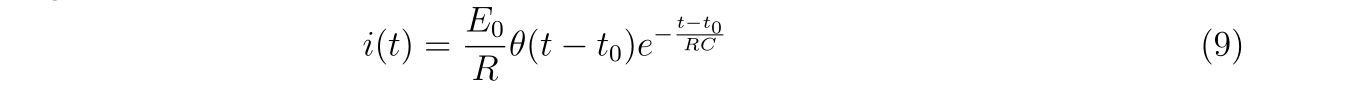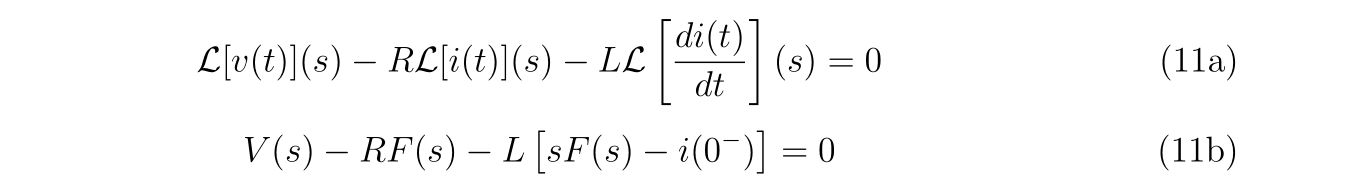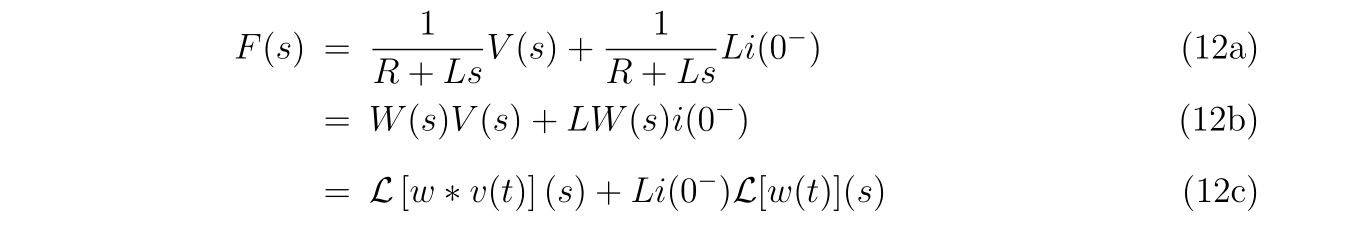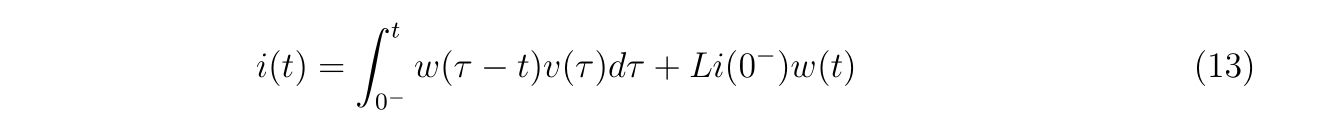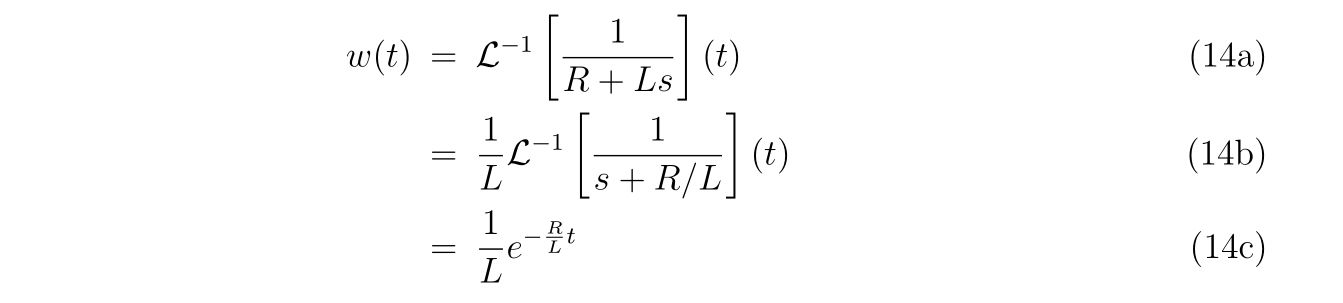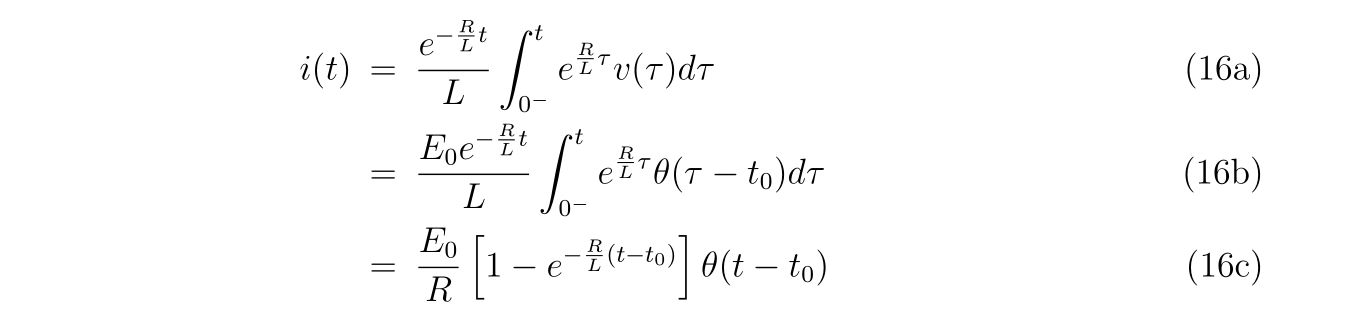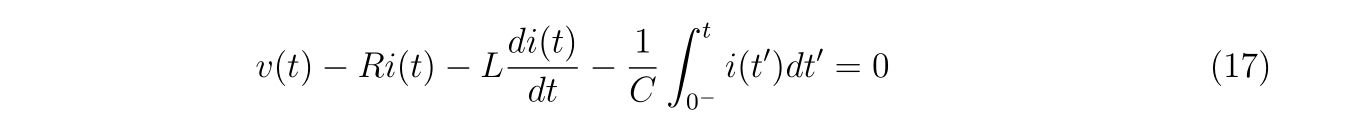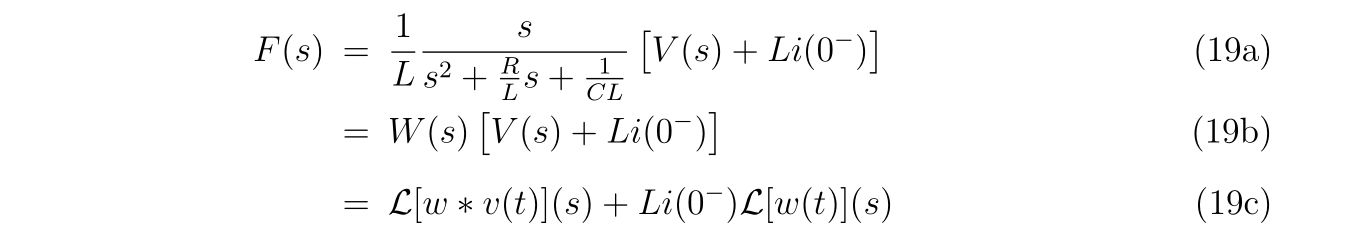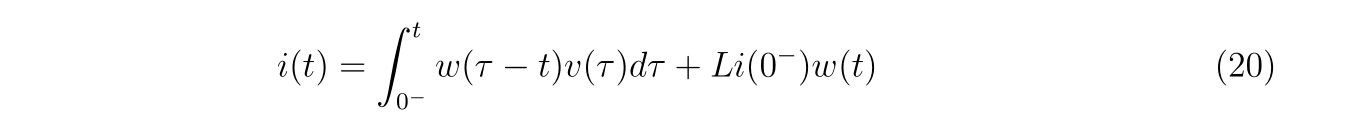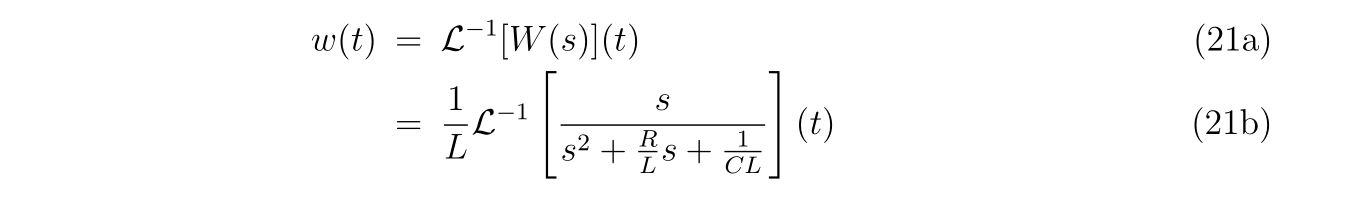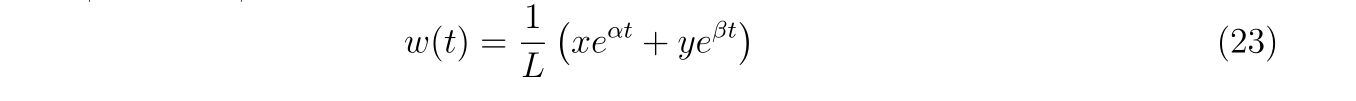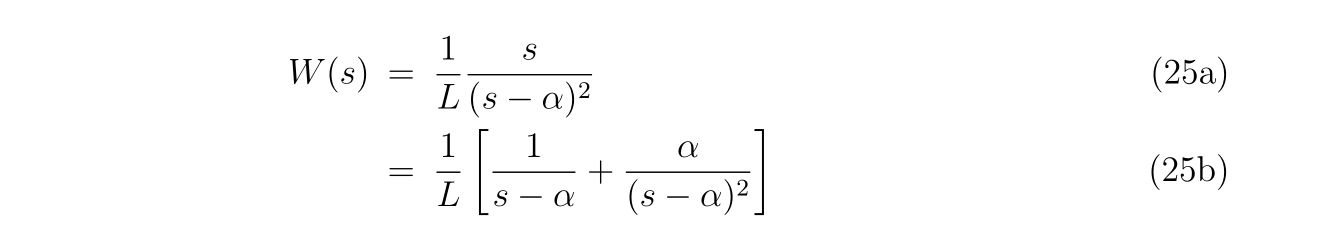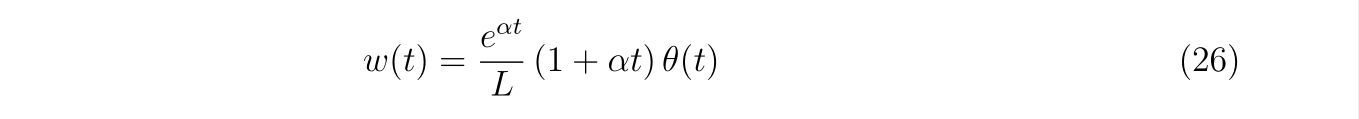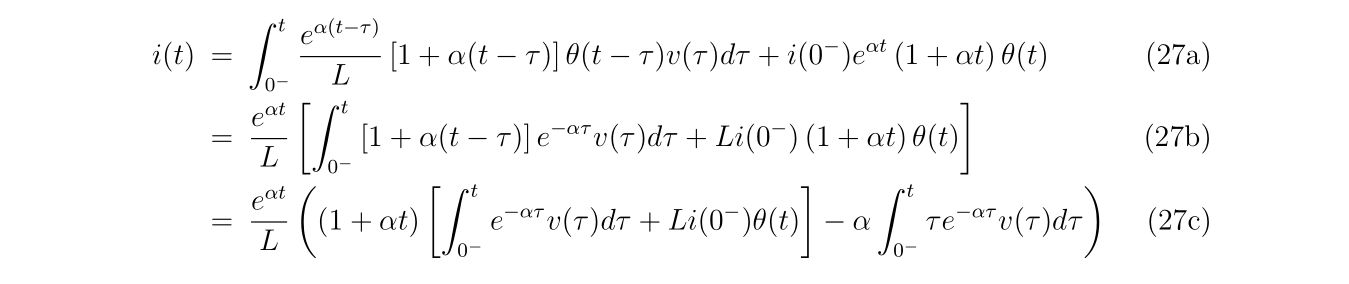RLC並列回路を考えます。
良くあるページではインピーダンスを考えるだけでよし、としていますが、過渡現象が知りたいですよね。私はそうです。ですので、ラプラス変換を用いて解いていきましょう。
回路方程式を立てれば、
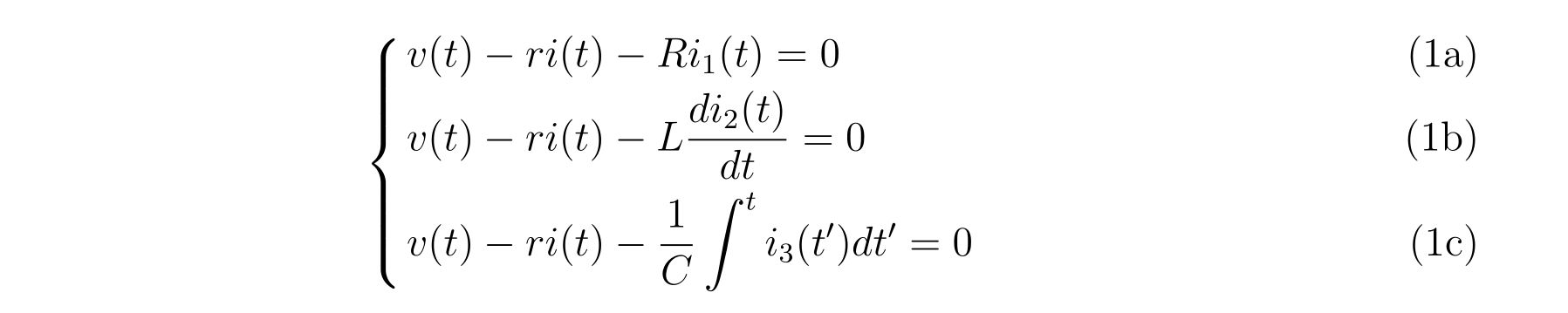
と
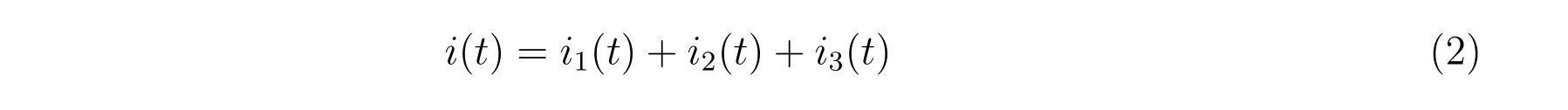
なります。この式(1)と式(2)の計4本の連立方程式を解いて、未知の関数\(i(t),i_1(t),i_2(t),i_3(t)\)を求めることが目標です。
電圧、電流のラプラス変換を
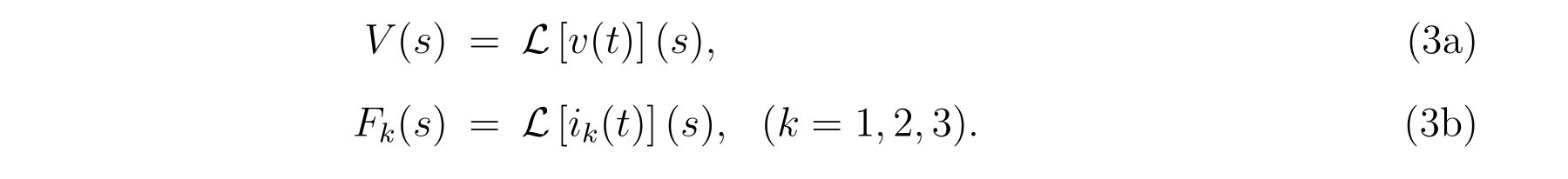
と書くことにします。式(2)を式(1)に代入して、ラプラス変換を施せば、
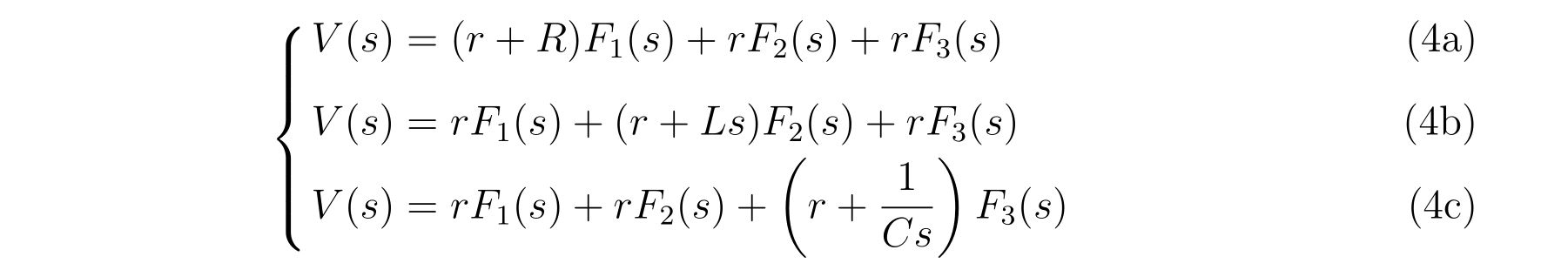
を得ます。もっと厳密に書けば、式(1b)のラプラス変換には\(i_2(0^-)\)という項が含まれますが、\(i_2(0^-)=0\), すなわち電源がオンになるまでは電流は存在しないと仮定します。
行列表示にすれば
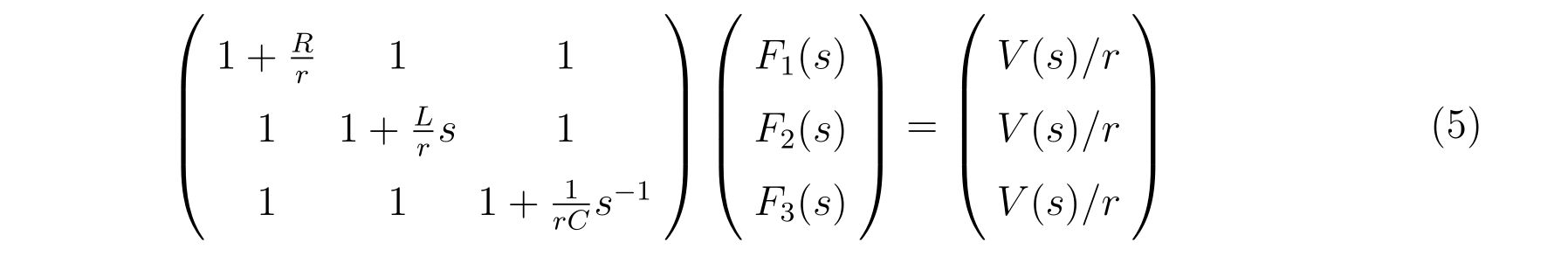
となります。関数\(F_k(s)\)にとって線形の問題です。表記を簡単にするために、
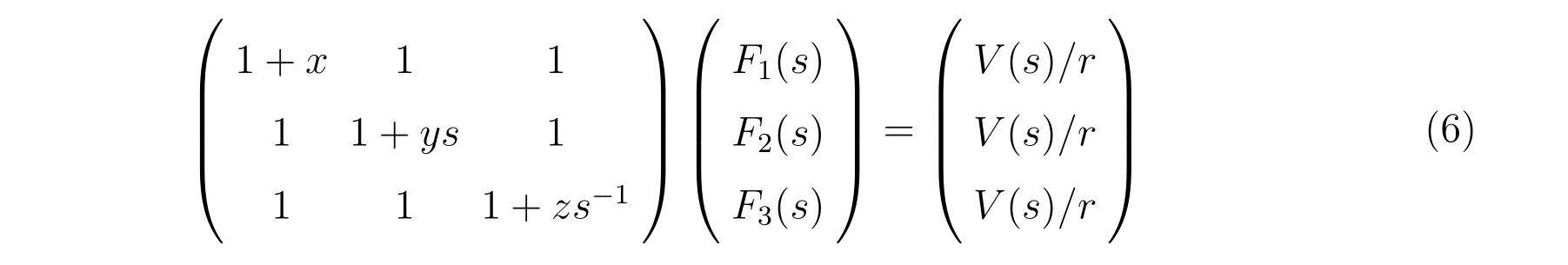
と書くことにします。ここで、\(x, y, z\)は
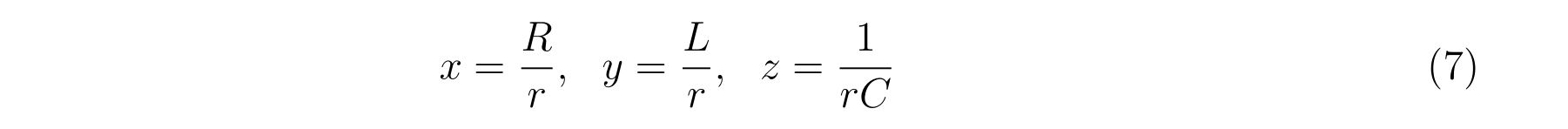
を意味します。ただの定数です。
クラメルの公式を用いて式(6)を解きます。関数
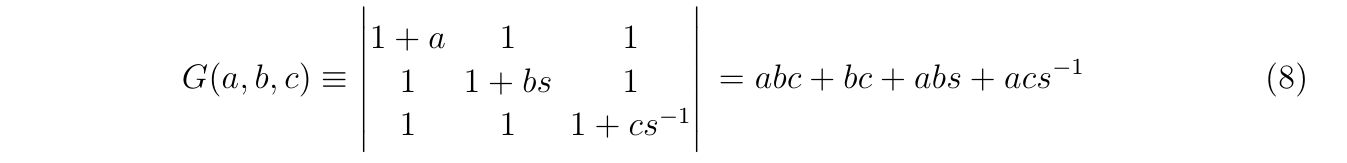
を定義すれば、式(6)の解は
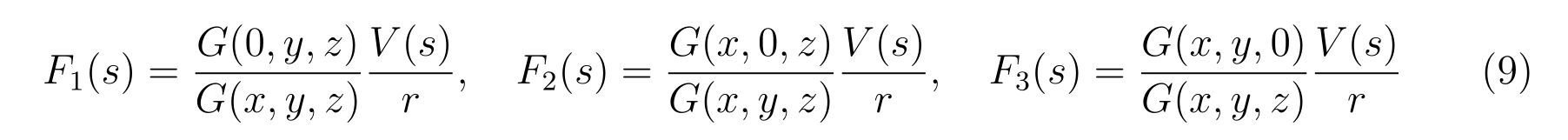
と書くことが出来ます。あらわに\(G(x,y,z)\)を書けば
\(\displaystyle
\begin{align}
~~~~~~~~~G(x,y,z)&=xyszs^{-1}+xys+yszs^{-1}+xzs^{-1} ~~~~~~~~~~(10a)\\
&=\frac{xy}{s}\left[s^2+z\Bigl(1+\frac{1}{x}\Bigr)s+\frac{z}{y}\right]~~~~~~~~~~(10b)\\
&=\frac{xy}{s}(s-\alpha)(s-\beta)~~~~~~~~~~(10c)\\
\end{align}\)
と表すことが出来ます。ここで、\(\alpha, \beta\)は
\begin{align}
s^2+z\Bigl(1+\frac{1}{x}\Bigr)s+\frac{z}{y}=(s-\alpha)(s-\beta)~~~~~~~~~~(11)
\end{align}
を満たすような解として書きました。
以降、\(\alpha, \beta\)は同じでは場合を考えていきます。
具体的に式(9)に現れる量を計算していけば、
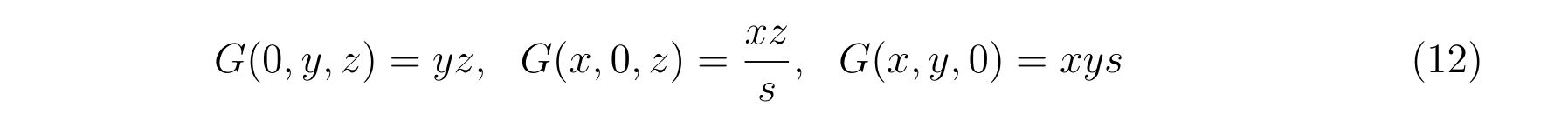
となります。それぞれ、
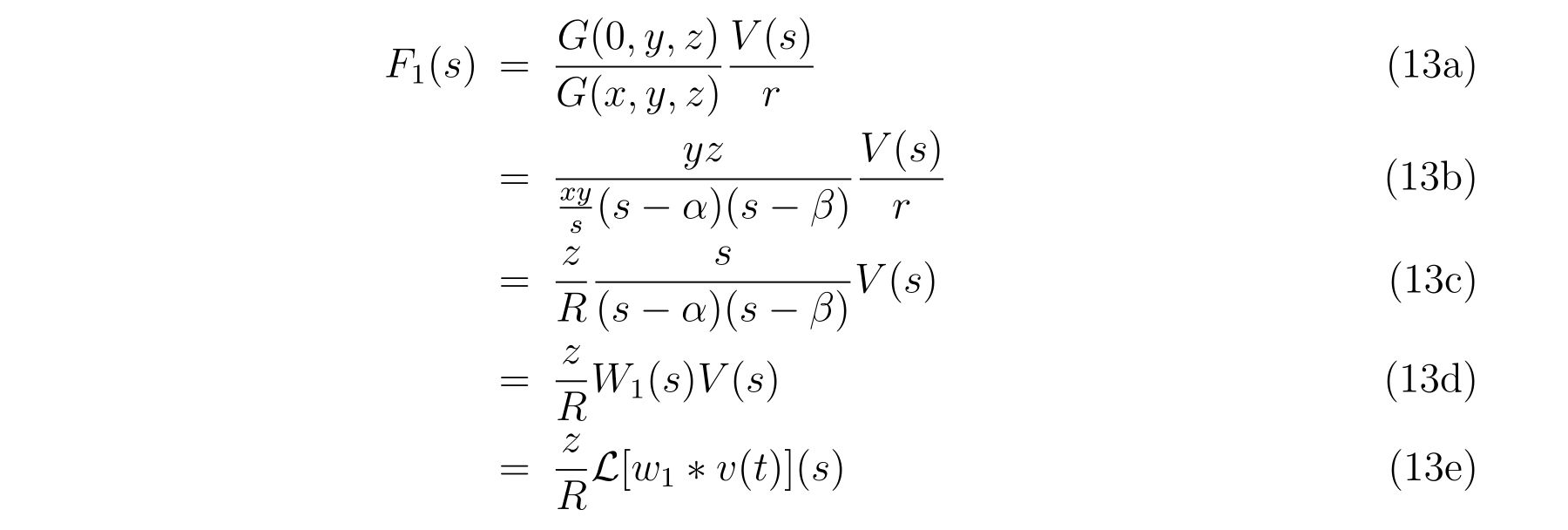
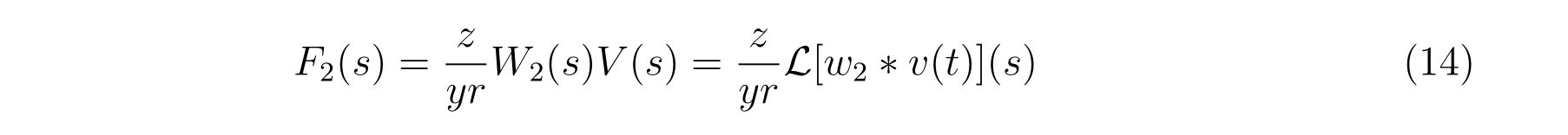
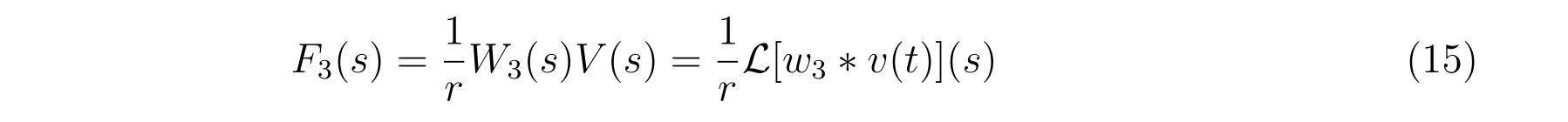
という結果が得られます。ここにいたるまでに、
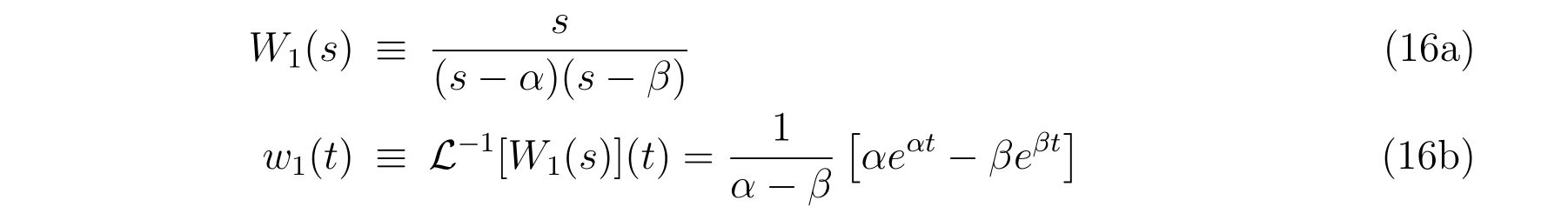
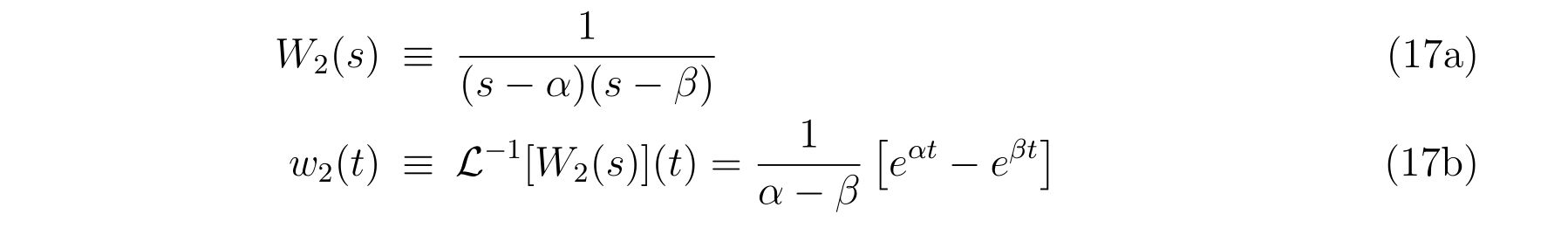
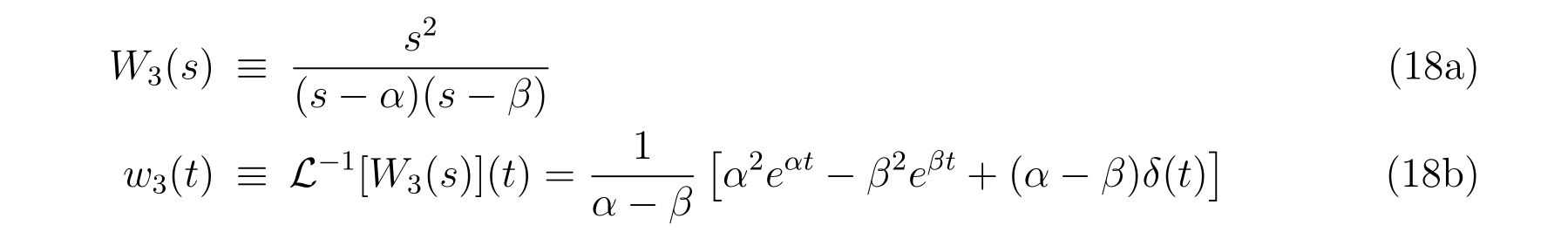
という関数を定義しました。
すると、それぞれの電流は
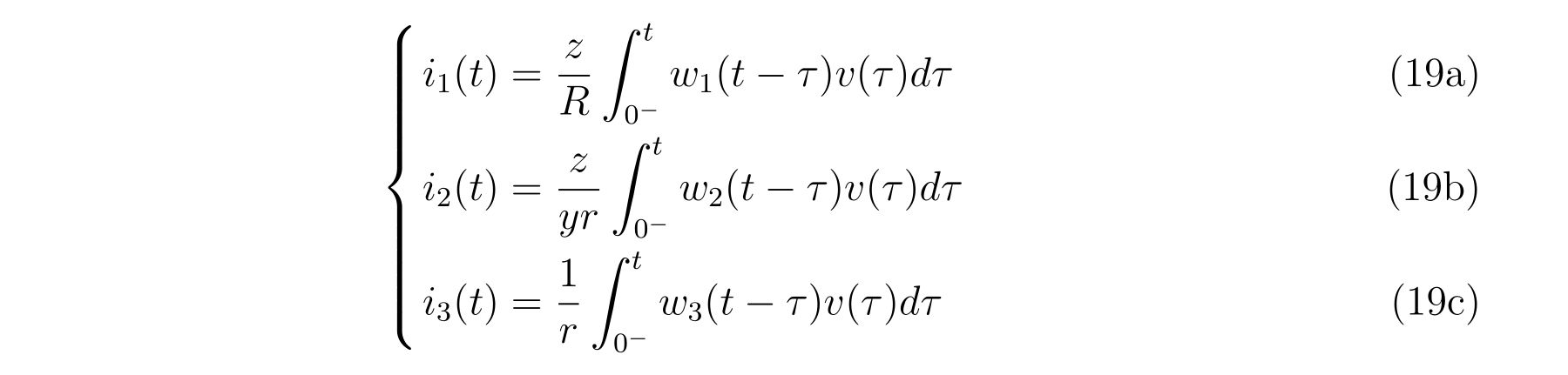
と書くことができ、具体的に
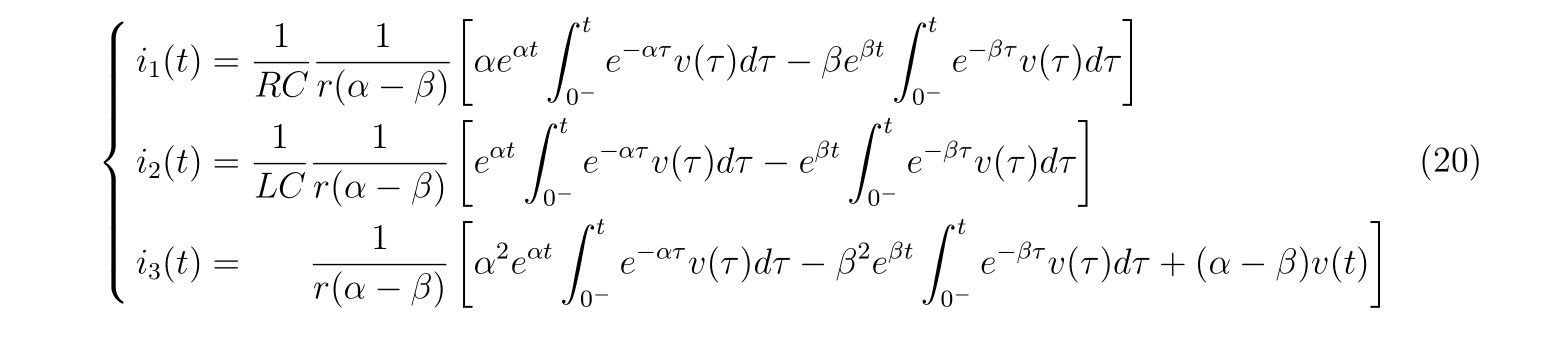
と求められます。
この結果を導くにあたって使用した仮定をまとめますと、
1. \(\alpha\ne \beta\)
2. \(i(t\lt 0)=0\)
という仮定の下、導き出された結果です。
導いた式(20)が合っているのか、直流電圧源を考えて考察してみましょう。
直流電圧源が時刻\(t=t_0\geq 0\)にスイッチオンする場合、電圧は
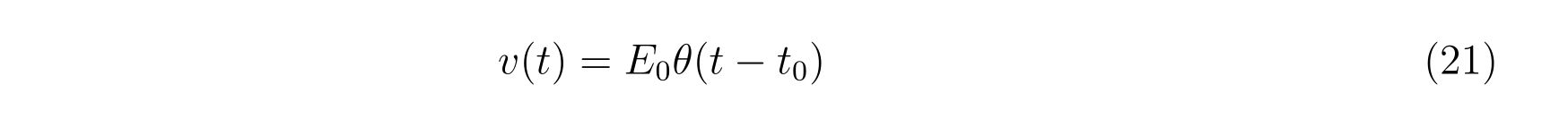
と書くことが出来ます。式(20)に出てくる積分は

と計算できますので、それぞれの素子を流れる電流は

と書きあらわすことが出来ます。
では、\(t\to\infty\)の漸近形を考えてみましょう。
\(t\to\infty\)の振る舞いは指数関数の型の\(t\)にかかる係数の実部の符号によって支配されます。式(11)より、具体的に\(\alpha, \beta\)を書くと

と求められます。今、\(R, C, L\)は全て正の実数ですので、ルートの項がその前の項の絶対値よりも大きくなることはありません。
よって、\(\text{Re}(\alpha)\lt 0, \text{Re}(\beta)\lt 0\)が導けます。すなわち、
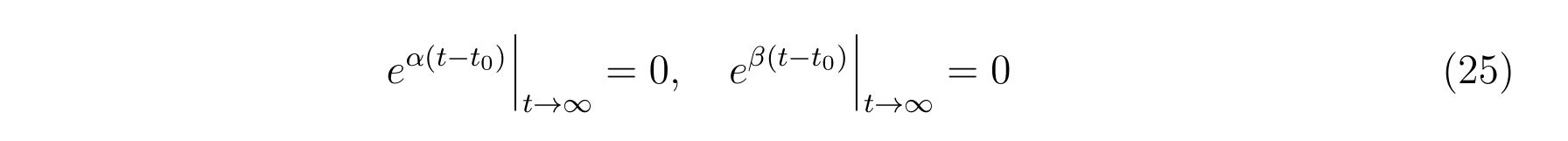
という結果です。
これを式(23)に代入すれば、
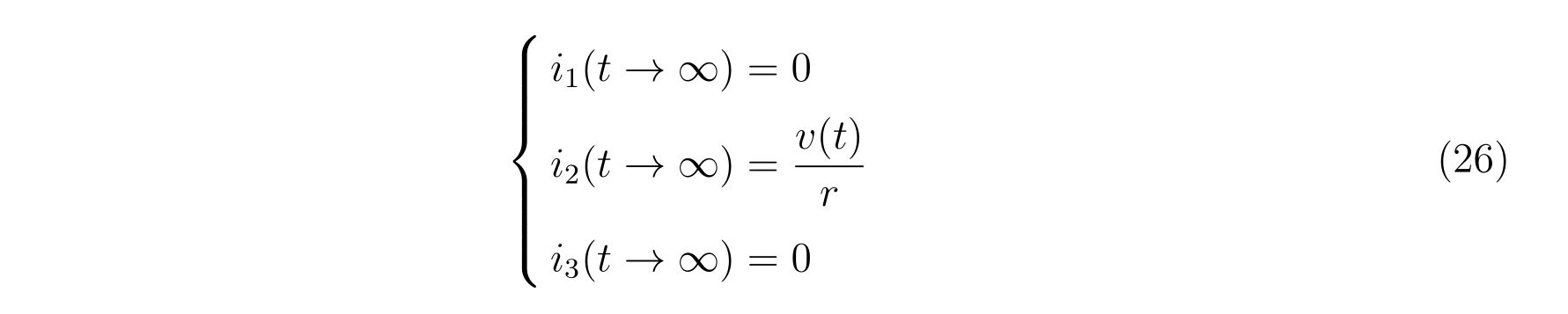
という結果が得られます。
電源が入った後に系が十分に落ち着いた定常状態では、コンデンサーは開放、コイルは短絡されたものと見なしてよいので、その結果に見合った振る舞いであることが分かります。
メモとして書いておきますが、式(11)を計算するにあたって\(\alpha \beta\)を計算する必要があります。これは式(24)から求めるのではなく、式(11)の右辺を展開して、\(s^0\)の項を比較すれば

という結果が得られます。