水中にBB弾が入った時の軌道は計算できるのでしょうか?
もしも水中での軌道が分かったのならば、そこから回転量、初速が分かるはずです。
まとめ
目的
- ハイスピードカメラを用いず、空気中で50mに及ぶ軌道を追わずに回転量を知ることが出来るか?
- 弾道計算(BB弾)の理論の検証
方法
- 水槽に向けてエアガンを撃った軌道とBB弾の弾道計算理論による軌道と比較
結論
- 水中の軌道は定性的に一致
- 定量的に合うのは到達距離、合わないのは水中での揚力
- 水中の軌道から回転量を知るには理論的に不十分
- まとめ
- きっかけ
- 方針
- 理論上の問題
- 実験上の問題
- 実験と理論の比較
- 理論で回転の減衰を入れないと?
- 参考文献
弾道計算に関するその他ページ
弾道計算(BB弾)の理論
BB弾の回転量について(実験との比較)
弾道計算(BB弾)の結果
弾道計算の結果2, 比較と詳細データ
弾道計算(BB弾)のコード(fortran90)
バレル内部でのBB弾の方程式
水中下でのBB弾の弾道計算←今ここ
[adsense1]
きっかけ
つい先日、こんな動画を見つけました。
夏休み 自由研究? BB弾水に撃つと?検証してみた。 マック堺 エアガンレビュー
水中の軌道じゃないですか。面白そう!
計算できない理由は無い。
式もある、プログラムもある。ならやってみよう。
がきっかけです。何故計算しようと思ったか?素晴らしい理由はありません。そこに物理があるからです。
方針
厳密さはそこまで求めません。
これには理由が2つあり、
- 水中を想定して作った理論ではないため、水の揺らぎが与える影響が不明。
- 実験がされた動画の縮尺、距離、回転量を見積もれない。
だからです。詳しい理由は以下の通り。
理論上の問題
空気も水も同じ流体ですが、その特性は大きく違います。

大気中の密度は低く、BB弾の密度と比べても0.1%未満です。そのため、大気の揺らぎがBB弾の影響することは無く、無視できるだろうと予想できます。
しかし、水ではBB弾の半分程度の密度になるために無視はできません。これは、0.1gのBB弾が詰まった容器に0.2gのBB弾を打ち込むようなものです。なので、容器が揺らぐとBB弾もそれにつられて動きます。
なので、現状のBB弾の弾道計算理論では考慮していない効果が現れるはずです。
荒っぽいですが、水は全く揺らいでいないし、揺ぐこともないと考えましょう。
この近似の下で、計算と実際の軌道が程度一致するのかを確かめていきます。
実験上の問題
実験の動画は軌道がはっきりわかるくらいのハイスピードカメラが使われています。
しかし、動画の時間、位置スケールが分からない点と回転量が分からないため、大雑把な値しか見積もれません。
せめて、同じ回転量で大気中の軌道があれば何とかなったかもしれませんが、無い以上は仕方ありません。
よって、方針としては
位置はBB弾のサイズから見積もり、
時間の情報は軌道だけに注目することで無くし、
回転量は数値計算する時の回転量を変えていって、重なる軌道があるかどうか?
で考えで行きます。
[adsense2]
実験と理論の比較
理論上の式を数値計算で解きます。数値計算で用いる数式は弾道計算(BB弾)の理論で導いた、空気抵抗、揚力、回転の減衰を考慮した運動方程式です。
まず、マック堺様による実験動画[1]からサイズ、入射角などを見積もります。
スクリーンショットをとって、BB弾の位置を等間隔に撮っていったのが下の画像になります。
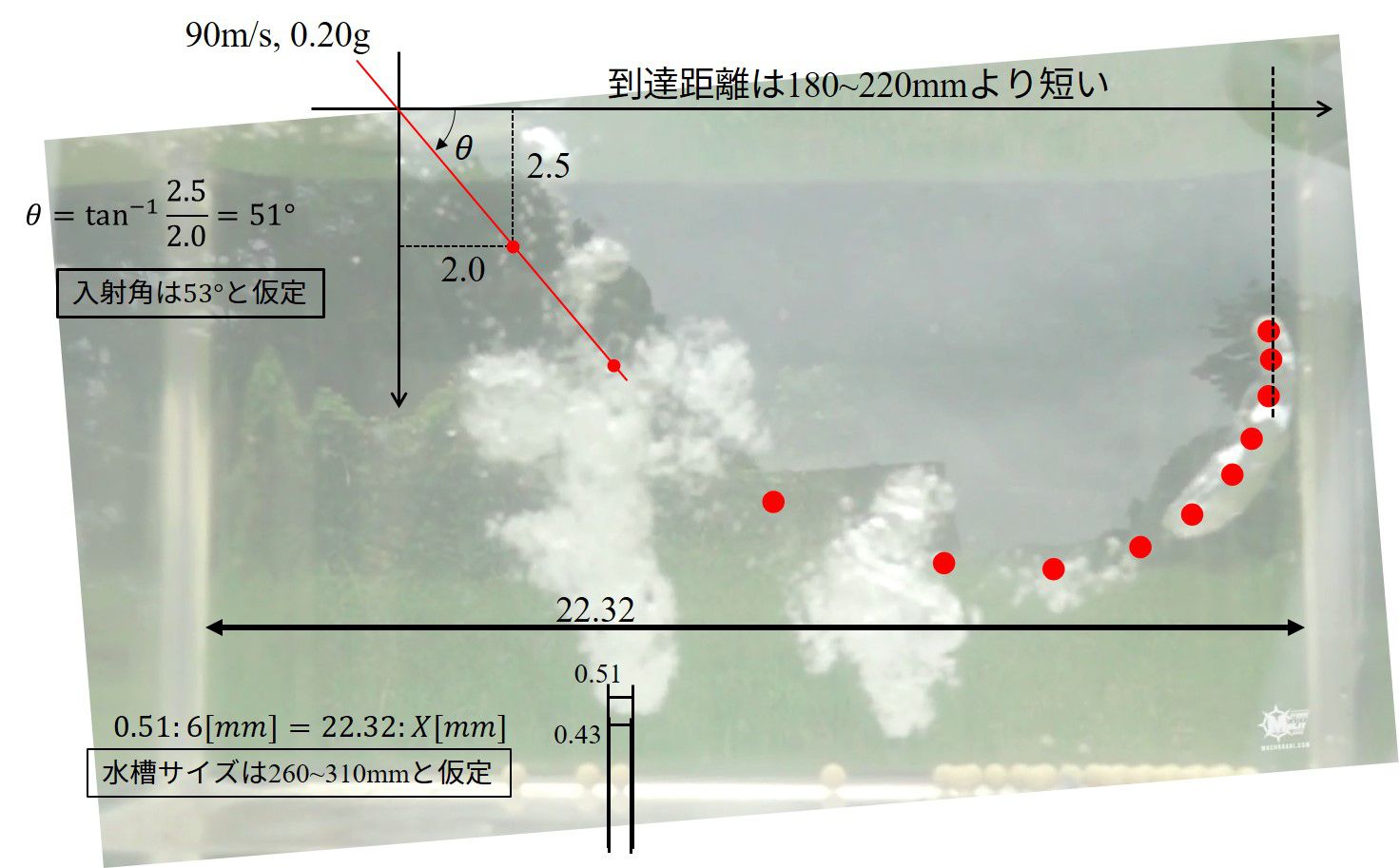
入射角の推定方法などは画像を見ていただければわかると思います。
画像から
入射角:51[度](→53[度]と推定)
入射位置からの到達距離:18~22[cm]
と分かりました。
重さ、初速は動画上で0.20g, 90m/sと紹介されていたのでそれを用います。
水中ではカーブするため、水中の2点間から導いた角度よりも大きくなることは確実です。
53度という値は数値計算で得られた軌道から53度位が良さそうだ、という推定をしました。
上記パラメータを利用し、
水の密度を\(1000[\mbox{kg/m}^3]\),
粘度を\(10^-3[\mbox{Pa}\cdot \mbox{s}]\)
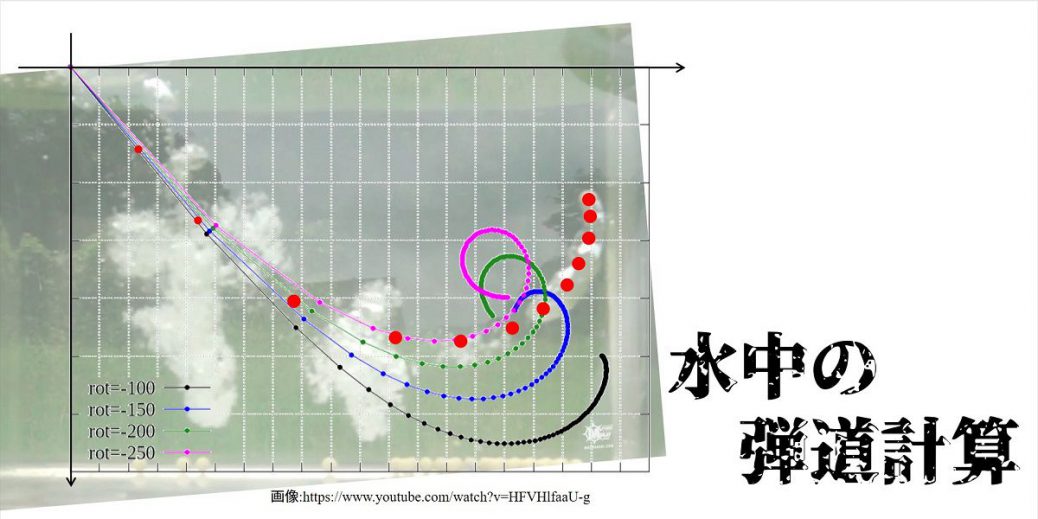
として回転量を変えていった時の軌道は以下のようになります。

実験の状況から、横軸は拡大されて見えているはずなので、BB弾を打ち込んだ位置の到達距離は、推定した一番短い距離を利用しています。
図中の赤い大きな点が実験のBB弾の位置で、線と点で表した4つの線が数値計算です。4つの黒、青、緑、紫は回転量の違いを表し、順に100、150、200、250回転/秒で計算した結果です。
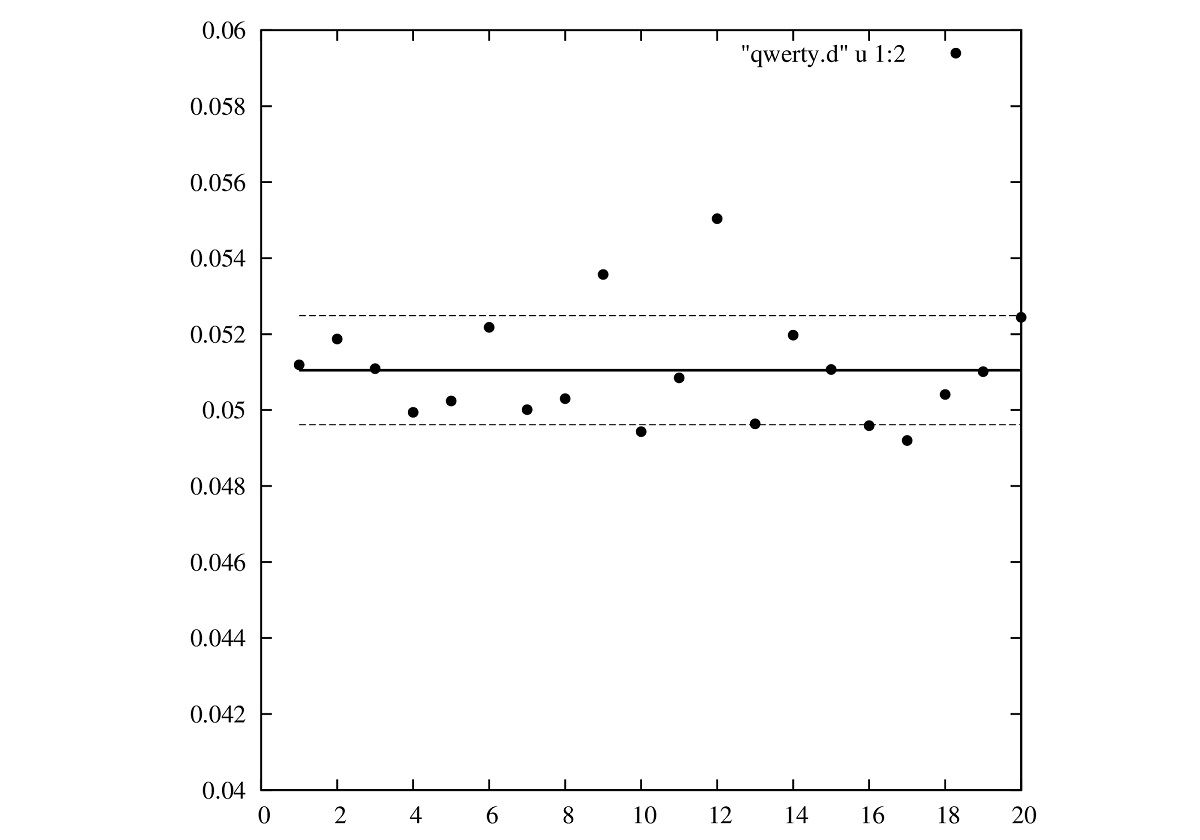
この回転数は妥当なものです。200回転の場合で大気中を想定し同じパラメータで計算しますと

のようになり、ホップが効かな過ぎず効き過ぎずの妥当な軌道になっています。
水の中を全く想定していない理論だとはいえ、良い結果だと思います。
特に、到達距離が数値計算でも20cm前後であることが定量的に再現できたのは大きな成果だと思います。また、水中でも揚力によって上昇することが定性的に再現できました。
揚力について、定量的に異なっています。実験では水面-最下点の半分以上上昇しているように見えますが、計算ではそこまで上昇しません。
空気が入っていることが大きな原因だと思いますが、はっきりとはわかりません。
先ほども述べた通り、水が揺らぐ効果は全く入っていないためです。
もしかするとエアガンを水中に沈め、空気が入らない状態で発射すればよいと思いますが、エアガンが壊れるので現実的ではありません。
銃口に膜でも作って、その膜を通してBB弾の衝撃をうまく伝わらせれば何とかなるかもしれませんが、今度は回転が無くなってしまいます。
ホップのゴムパッキンのすぐ後ろに膜でも作れば何とか…?
理論で回転の減衰を入れないと
回転の減衰を入れないとどうなるでしょうか?
大気中の場合はさほど重大な問題ではありませんでしたが、水中では以下のようになりました。200回転/秒で計算しています。
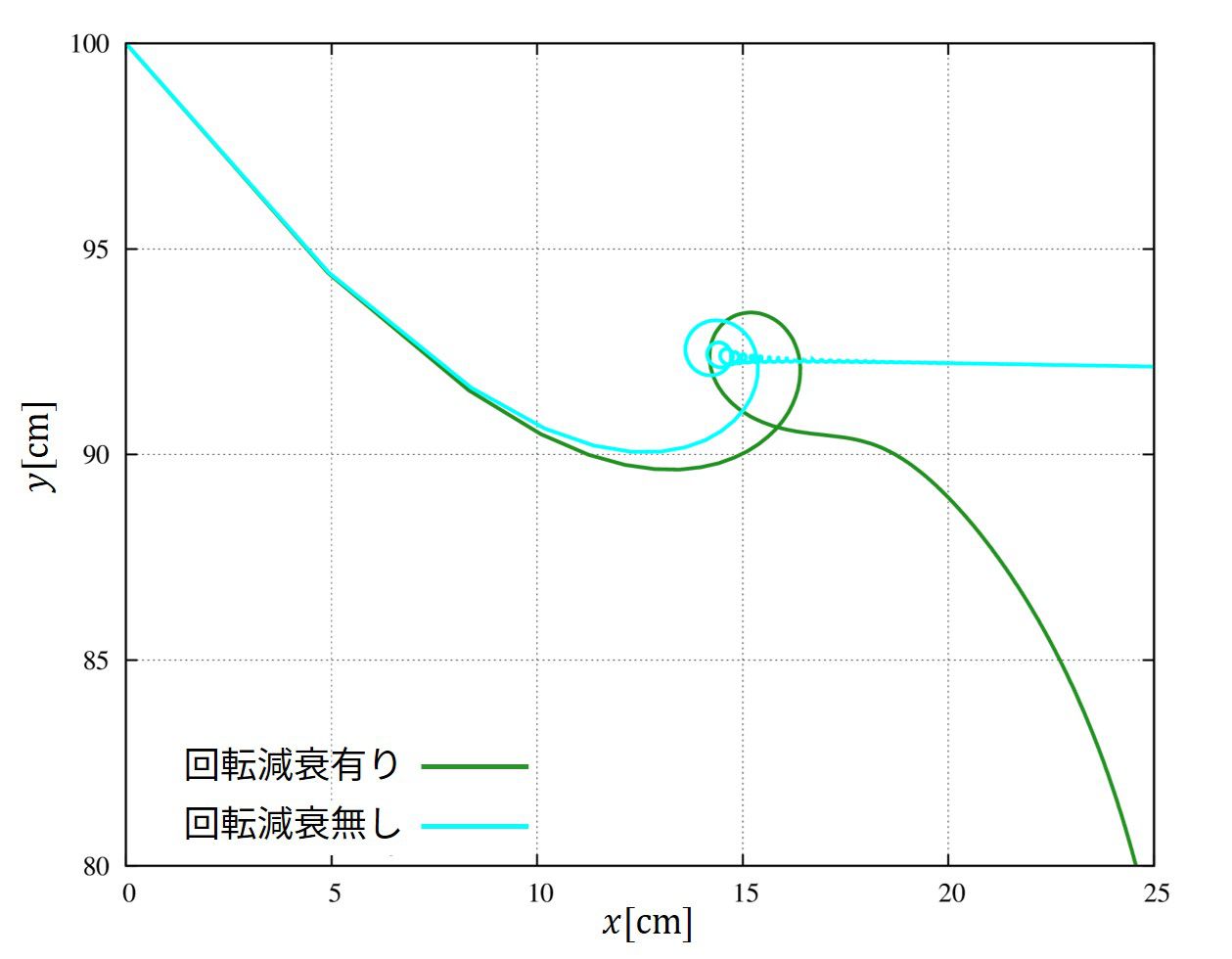
回転の減衰を入れない計算は図中、水色の線であり、明らかに物理が破綻しています。
回転の減衰を入れた計算は図中、緑色の線であり、直感と合い、良い振る舞いをしていることが分かります。
参考文献
[1]夏休み 自由研究? BB弾水に撃つと?検証してみた。 マック堺 エアガンレビュー
※このページでのみ、動画のスクリーンショットに変更を加えた画像の使用許諾済み。
[2]水・空気の物性 密度 粘度 動粘度
[3]弾道計算(BB弾)の理論 -シキノート