月別アーカイブ: 2016年7月

プログラミングと数値計算

4倍精度演算(fortran90)

コメントする

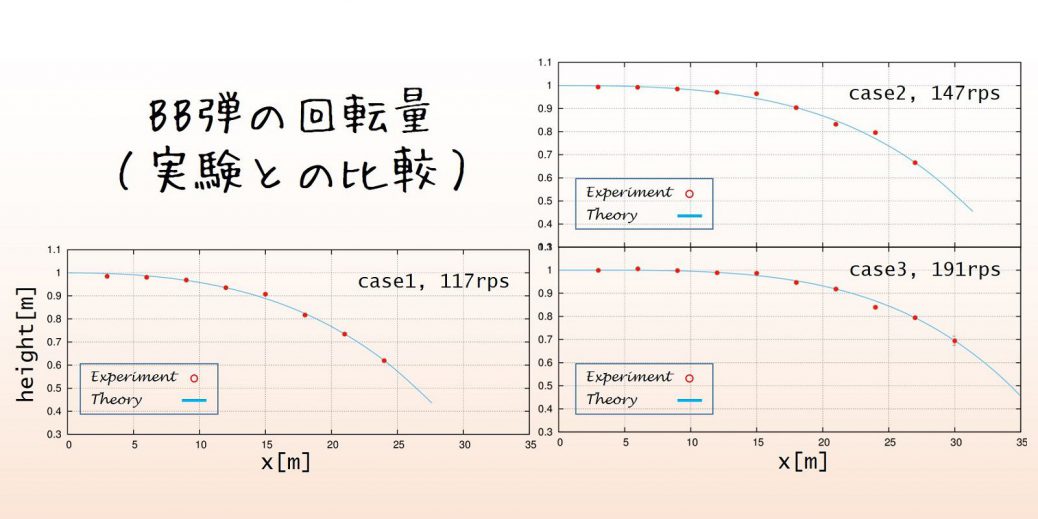
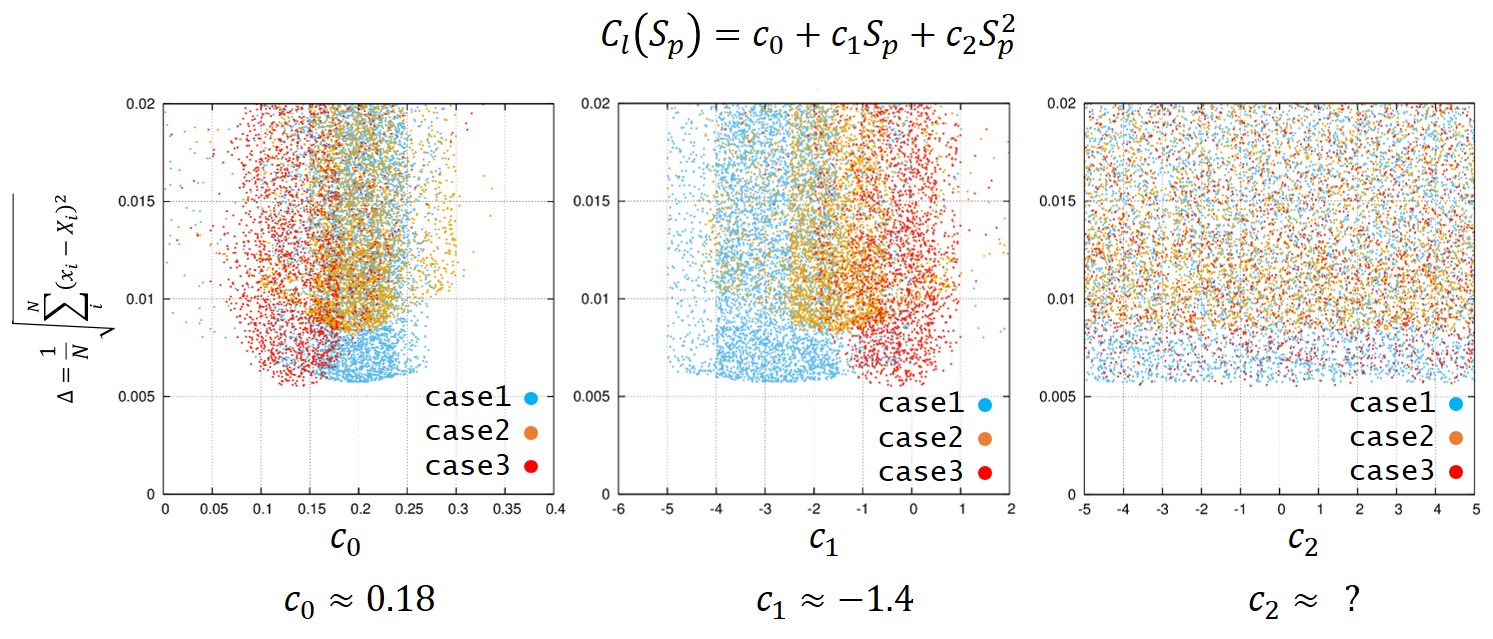
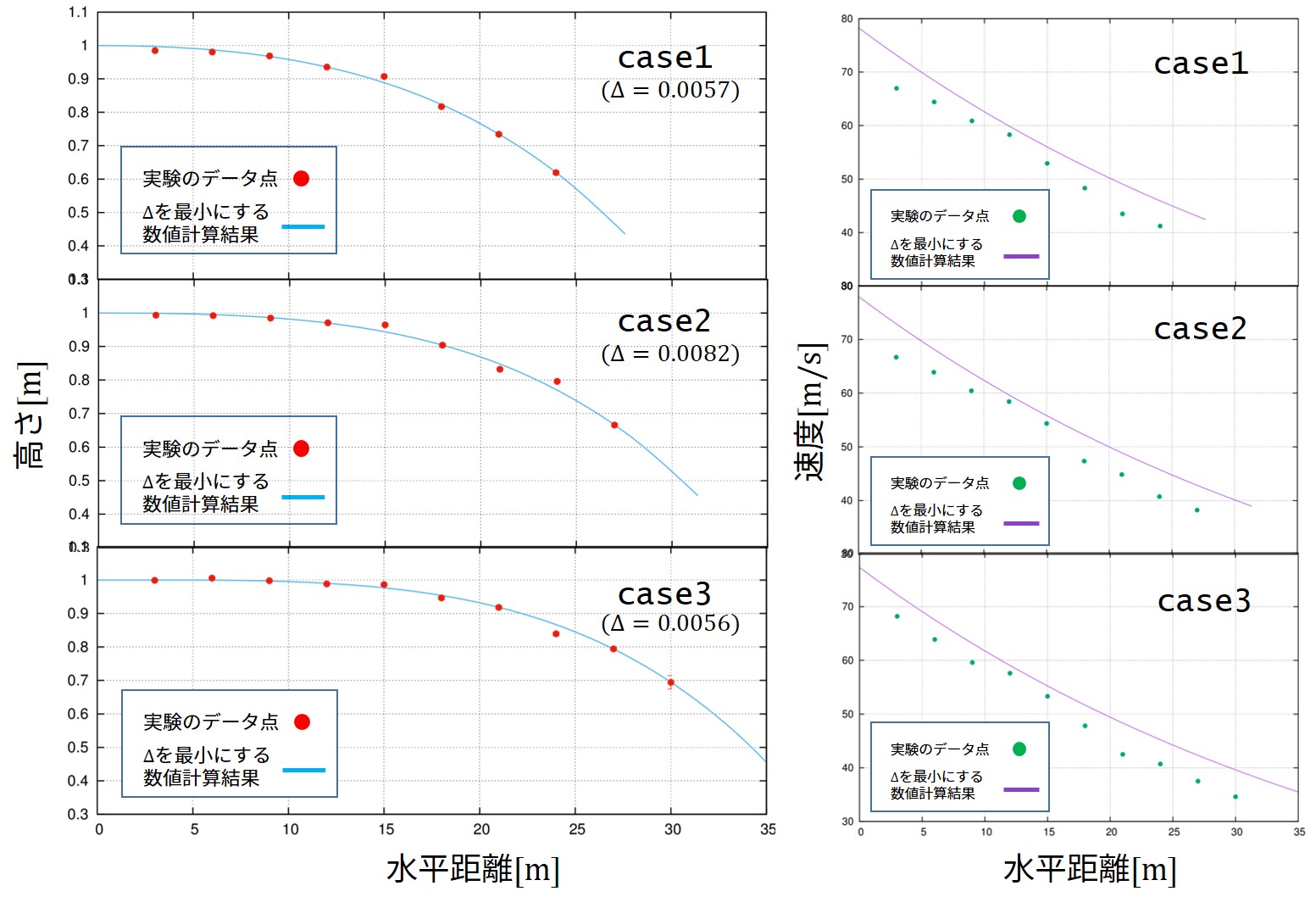
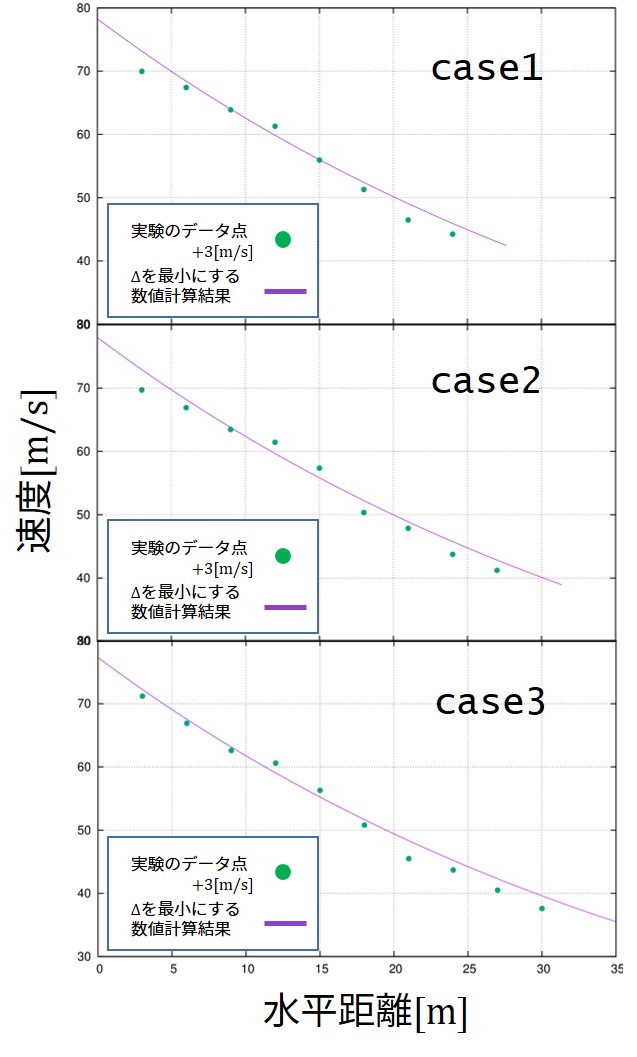
fortran90において4倍精度で計算を行います。

メリット
情報落ちの回避
桁落ちの回避

デメリット
計算速度が遅い(倍精度の40~50倍!)
4倍精度に対応しているライブラリが少ない

計算式を工夫して、どうしても4倍精度でないと解けない場合のみ4倍精度を使うことを考えましょう。

  1. 4倍精度の存在理由
  2. 4倍精度演算の組み込み関数
  3. 4倍精度陽的ルンゲクッタ法(刻み幅制御)
  4. 4倍精度陰的ルンゲクッタ法(刻み幅制御)
  5. 4倍精度の一般行列の対角化(複素非エルミート)
  6. 4倍精度のLU分解による連立方程式

4倍精度の存在理由

4倍精度は倍精度演算を正しく行うための補助的存在です。
初めから最後まで4倍精度で行うことはほとんどありません。
4倍精度が効果を発揮する桁落ちの例を考えましょう。

計算
\(
1-(1+\frac{10^{-10}}{3})
\)
を考えます。
答えは\(-3.333333\cdots\times 10^{-11}\)です。
数値計算で倍精度と4倍精度で試してみますと、

program main
  implicit none
 
  write(6,*)1d0-(1d0+(1d-10)/3d0)
  write(6,*)1q0-(1q0+(1q-10)/3q0)
 
  stop
end program main

であり、実行結果は

$ ifort main.f90
$ ./a.out
 -3.333333609134570E-011
 -3.333333333333333333333342109654793E-0011
$

となります。計算過程で工夫もできないような場合、4倍精度を利用して

program main
  implicit none
  double precision::a
  real*16::b
 
  b=1q0-(1q0+(1q-10)/3q0)
  a=dble(b)
  write(6,*)a
 
  stop
end program main

として途中だけ4倍精度にして計算する、これが4倍精度の存在理由です。
上記プログラムを実行すると

-3.333333333333333E-011

となります。

想定

4倍精度演算は決まった書き方が無く、コンパイラに依存します(補足1)。
ここでは、
intel®fortran コンパイラ(ifort (IFORT) 16.0.2 20160204)
と
gnu fortran コンパイラ(GNU Fortran (Ubuntu 4.8.4-2ubuntu1~14.04.1) 4.8.4
)
の二つで動作することを考えます。

4倍精度変数の宣言方法

4倍精度実数、4倍精度複素数は

real*16::a
complex*32::c

と変数宣言をしましょう。
値を代入する際は、

a=1q0
c=cmplx(1q0,2q0,kind=16)

として”q”を用います。
※”c=cmplx(1q0,2q0)”としてはダメです。
複素数への代入はcmplx(実部、虚部、精度指定)でないといけません。
ifortだけであれば、qcmplxで自動的に精度が4倍精度指定されますが、gfortranではkindで指定しないと代入されません。実際、

program main
  implicit none
  complex*32::z

  z=cmplx(1q0/3q0,1q0)
  write(6,*)z  
 
  z=cmplx(1q0/3q0,1q0,kind=16)
  write(6,*)z

  stop
end program main

を実行すると、gfortranでもifortでも

$ ifort main.f90
$ ./a.out
 (0.333333343267440795898437500000000,1.00000000000000000000000000000000)
 (0.333333333333333333333333333333333,1.00000000000000000000000000000000)
$
$ gfortran main.f90
$ ./a.out
 ( 0.333333343267440795898437500000000000      ,  1.00000000000000000000000000000000000      )
 ( 0.333333333333333333333333333333333317      ,  1.00000000000000000000000000000000000      )
$

という結果を得て、正しく値が代入されません。

[adsense1]

4倍精度演算のための組み込み関数

基本的には総称名を用いるのが良いと思います[1,2]。

a=sin(4q0)
c=exp(cmplx(3q0,1q0,kind=16))

倍精度から4倍精度に変換する際は、

a=sin(4d0)*1q0
c=cmplx(exp(3q0),kind=16)

とすると良いでしょう。あとは他の精度の時と同じです。

ルンゲクッタ法の4倍精度刻み幅制御

4倍精度でルンゲクッタ法を行います。(刻み幅制御ルンゲクッタ法についてはルンゲクッタ法の説明と刻み幅制御をご覧ください。)
対象とする微分方程式は
\(
\displaystyle \frac{d^2y}{dx^2}=\left(-\frac{1}{4x^2}+\frac{i}{x}-1\right)y
\)
を初期条件
\(
\begin{align}
\left. y(x)\right|_{x=1}=\exp(i) \\
\left. \frac{dy(x)}{dx}\right|_{x=1}=\left(\frac{1}{2}+i\right)\exp(i)
\end{align}
\)
の条件下で解くものです。解析解は\(y(x)=\exp(ix)\sqrt{x},\frac{dy(x)}{dx}=\left(\frac{1}{2x}+i\right)\exp(ix)\sqrt{x} \)となります。
メインのコードは

program main
  use qRKmod
  implicit none
  integer::i,N,Nx,info
  real*16::dx,tol,xbound,x0,tx
  real*16,allocatable::x(:)
  complex*32,allocatable::y(:),ss(:)
  complex*32::rkfc
  external::rkfc
 
  N=2
  allocate(y(1:N))
 
  x0=1q0; dx=1000q0; Nx=2
  allocate(x(0:Nx-1))
  do i=0,Nx-1
     x(i)=x0+dble(i)*dx
  enddo

  y(1)=exp(cmplx(0q0,1q0,kind=16))
  y(2)=cmplx(0.5q0,1q0,kind=16)*y(1)

  call qrk_preparation("rkf45")

  tol=1q-18
  write(10,'(3e30.17e4)')x(0),real(y(1)),imag(y(1))
  do i=1,Nx-1
     info=0; tx=x(i-1); xbound=x(i)
     call qrkf45_e(rkfc,tx,y,xbound,info,tol)
     if(info.eq.-1)write(6,'(A,f10.5,A,f10.5)')"strange point between ",x(i-1)," and ",x(i)
 
     write(10,'(3e30.17e4)')x(i),real(y(1)),imag(y(1))
  enddo
  write(6,*)x(0),y(1)
 
  call qrk_deallocation("rkf45")
 
  stop
end program main
!----------------
function rkfc(N,x,y,s)
  implicit none
  integer,intent(in)::N,s
  real*16,intent(in)::x
  complex*32::y(1:N)
  complex*32::rkfc
 
  rkfc=0q0
  if(s.eq.1)then
     rkfc=y(2)
  elseif(s.eq.2)then
     rkfc=(-1q0/(4q0*x*x)+cmplx(0q0,1q0,kind=16)/x-1q0)*y(1)
  else
     write(6,*)"unknown s, program stop"
     stop
  endif
 
  return
end function rkfc

で、4倍精度用のルンゲクッタ法のモジュールはこちら。

1ステップ当りの精度を18桁に設定し、実行すると
実行すると、

$ ifort qrkmod.f90 qmain.f90
$ ./a.out
   1.00000000000000000000000000000000      
 (-12.4004402201339396388318226191018,29.1071998369283977905998988164457)
$
$ gfortran qrkmod.f90 qmain.f90
$ ./a.out
   1.00000000000000000000000000000000000       ( -12.4004402201339396388318226207936776      ,  29.1071998369283977905998988157304999      )
$

という結果を得ます。
ここに表示されているのは、解析解の\(x=1001\)での値で、
-12.400440220133925015780697384759199505100325758422733906… +
29.107199836928403740368952842025341239069669658649312423… i
が厳密値となります。
x=1001で数値計算解と比較すると15桁一致していることが分かります。

計算時間は倍精度計算の約40倍かかりますが、どうしても16桁近い精度が欲しい場合や桁落ちが激しいことが分かっている場合には、途中を4倍精度で演算して後で倍精度に戻す、と言う方法が良いでしょう。

[adsense2]

計算時間について

ルンゲクッタ法で、倍精度、4倍精度を比較します。
中身が複雑なのであまり良い比較方法ではありませんが、目安としてどの程度か分かるでしょう。
CPU時間を計測します。

上記微分方程式を10回解いたとき、
倍精度では
0.298 [秒]
4倍精度では
11.268[秒]
でした。
約40倍遅いことが分かります。
計算が工夫できるならするべきです。むやみに4倍精度を使ってはなりません。

補足1)コンパイラに依存してしまうとは？

例えば、
\(1/3\)を計算してみましょう。

program main
  implicit none

  write(6,*)qext(1d0/3d0)
 
  stop
end program main

”qext”は倍精度→4倍精度の型変換をする組み込み関数です。
このコードをifortで行うと計算が実行され、
実行結果

$ ifort main.f90
$ ./a.out
  0.333333333333333314829616256247391  
$

を得ます。しかし、同じコードをgfortranでコンパイルしようとすると、

$ gfortran main.f90
main.f90:4.12:

  write(6,*)qext(1d0/3d0)
            1
Error: Function 'qext' at (1) has no IMPLICIT type
$

となり、コンパイルが出来ません。
この場合、型変換用の組み込み関数を使わないで、

program main
  implicit none

  write(6,*)(1d0/3d0)*1q0
 
  stop
end program main

とするのが良いでしょう。
異なる型の演算は高い方の型に合わせられることを利用します。
すると、どちらのコンパイラでもokで、

$ gfortran main.f90
$ ./a.out
  0.333333333333333314829616256247390993      
$ ifort main.f90
$ ./a.out
  0.333333333333333314829616256247391      
$

となります。
gfortranとifortで表示されている桁数が違うのは標準出力の違いだけのようです。
なぜなら、組み込み関数[3]
———————————————————–
precision:10進数で表現できる桁数
epsilon:機械精度(1にこの値を足しても1のままになる最大の値)
tiny:指数表現での最小値
huge:指数表現での最大値
———————————————————–
を使って調べると、

program main
  implicit none
  real*16::a
 
  write(6,*)precision(a)
  write(6,*)epsilon(a)
  write(6,*)tiny(a)
  write(6,*)huge(a)

  stop
end program main

実行結果

$ ifort main.f90
$ ./a.out
          33
  1.925929944387235853055977942584927E-0034
  3.362103143112093506262677817321753E-4932
  1.189731495357231765085759326628007E+4932
$
$ gfortran main.f90
$ ./a.out
          33
   1.92592994438723585305597794258492732E-0034
   3.36210314311209350626267781732175260E-4932
   1.18973149535723176508575932662800702E+4932
$

という結果が得られるからです。

4倍精度の陰的ルンゲクッタ法

4倍精度の陰的ルンゲクッタ法については
陰的Runge-Kutta法
に載せてありますので、そちらをご覧ください。

4倍精度の一般行列の対角化

複素非エルミート行列の対角化については
4倍精度の一般行列の対角化
に載せてありますので、そちらをご覧ください。

4倍精度のLU分解による連立方程式の解法

4倍精度のLU分解を用いた連立方程式の解法は
九州大学の渡部 善隆様が公開なさっているGECP(Gaussian Elimination with Complete Pivoting, 一般実行列に対する連立1次方程式の数値解を完全ピボット選択付き Gauss の消去法によって求める Fortran サブルーチン)
によって実現できます[4]。
http://yebisu.cc.kyushu-u.ac.jp/~watanabe/RESERCH/GECP/index.html。
再配布可能です。

参考文献

[1]9.58 CMPLX — Complex conversion function -The GNU Fortran Compiler(gfortran complex精度指定)
[2]第 3 章 FORTRAN 77 および VMS 組み込み関数 -Sun Studio 12: Fortran ライブラリ・リファレンス
[3]浅岡 香枝、平野 彰雄、”はじめてのFortran90”
[4]渡部 善隆, 一般実行列に対する連立1次方程式の数値解を完全ピボット選択付き Gauss の消去法http://yebisu.cc.kyushu-u.ac.jp/~watanabe/RESERCH/GECP/index.html

プログラミングと数値計算

ガウス=クロンロッド求積法

コメントする

ガウス=クロンロッド求積法と呼ばれる数値積分法です。

  1. ガウス=クロンロッド求積法の説明
  2. fortran90によるプログラム
    1. 15次ガウス=クロンロッド求積(\([-1\sim 1]\))
    2. 15次ガウス=クロンロッド求積(\([a\sim b]\))
    3. 61次ガウス=クロンロッド求積(\([a\sim b]\))
  3. 参考文献

説明

ガウス=ルジャンドル求積法の補助的な存在、というとらえ方でいいと思います。
通常はガウス=ルジャンドル求積法の誤差推定のために使われるらしいです。

積分
\(
\displaystyle \int_{-1}^{1} f(x) dx
\)
を、
\(
\displaystyle \int_{-1}^{1} f(x) dx \approx \sum_{i=1}^{2N+1} \omega_i f(x_i)+\mathcal{O}(x^{3N+1})
\)
として近似します。ここで、\(\omega_i\)は点\(x_i\)での重みを意味します。
\(\omega_i, x_i\)は任意に決められず、\(N\)をいくつにするかによって強制的に決定されます。

ガウス=クロンロッド求積法は次数(\(2N+1\))を用いたとき、被積分関数が
\(x^{3N+1}\)以下の多項式であれば厳密な積分値を返しますCHAPTER 5 Numerical Quadrature。
Nは次数。分点数と一致。

重要な事ですが、被積分関数が多項式ではない場合、あまりよくない積分結果になってしまいます。
例えば、積分
\(
\displaystyle \int_0^b \sqrt{x} dx
\)
を考えると、被積分関数が多項式で書けないので、精度はガクッと落ちます。
この理由は、被積分関数の微分が\(x=0\)で発散するためであり、高次の積分法になるほど顕著に表れます。

また、ルンゲ現象に代表される、高次で発生する様々な問題を排除するため、通常は積分区間を複数に分けて、低次の積分法を組み合わせて計算を行います。

[adsense1]

fortran90によるプログラム

以下のプログラムは15次ガウス=クロンロッド求積法のプログラムです。
これは、積分
\(
\displaystyle \int_{-1}^{1}e^{-x} dx = 2\sinh(1) \approx 2.350402387287602913764764
\)
を計算するプログラムとなっています。

program main
  implicit none
  integer::i,N
  double precision,allocatable::x(:),w(:)
  double precision::f,s
  external::f
 
  N=15
  allocate(x(1:N),w(1:N)); x=0d0; w=0d0
  call GaussKronrod15(x,w)
  s=0d0
  do i=1,N
     s=s+w(i)*f(x(i))
  enddo  
  write(6,*)s

  deallocate(x,w)  
 
  stop
end program main

function f(x)
  implicit none
  double precision,intent(in)::x
  double precision::f
 
  f=exp(-x)

  return
end function f

subroutine GaussKronrod15(x,w)
  !Gauss-Kronrod Quadrature Nodes and Weights
  !http://www.advanpix.com/2011/11/07/gauss-kronrod-quadrature-nodes-weights/
  implicit none
  double precision,intent(out)::x(1:15),w(1:15)
 
  integer::i
  integer,parameter::N=15
 
  x=0d0; w=0d0
 
  x( 8) = 0d0
  x( 9) = 2.077849550078984676006894037732449d-1
  x(10) = 4.058451513773971669066064120769615d-1
  x(11) = 5.860872354676911302941448382587296d-1
  x(12) = 7.415311855993944398638647732807884d-1
  x(13) = 8.648644233597690727897127886409262d-1
  x(14) = 9.491079123427585245261896840478513d-1
  x(15) = 9.914553711208126392068546975263285d-1  
  do i=1,7
     x(i)=-x(N-i+1)
  enddo
 
  w( 8) = 2.094821410847278280129991748917143d-1
  w( 9) = 2.044329400752988924141619992346491d-1
  w(10) = 1.903505780647854099132564024210137d-1
  w(11) = 1.690047266392679028265834265985503d-1
  w(12) = 1.406532597155259187451895905102379d-1
  w(13) = 1.047900103222501838398763225415180d-1
  w(14) = 6.309209262997855329070066318920429d-2
  w(15) = 2.293532201052922496373200805896959d-2
  do i=1,7
     w(i)=w(N-i+1)
  enddo

  return
end subroutine GaussKronrod15

実行結果は
2.35040238728760
となり、厳密値
2.350402387287602913
と全桁一致します。

区間変更

定義そのままでは\([-1\sim 1]\)なので、区間を変更しましょう。
区間変更は\(y=\frac{b-a}{2}x+\frac{b+a}{2}\)と変数変換をすれば、

\(
\begin{align}
\int_a^b f(x) dx &= \int_{-1}^{1} f(y) \frac{b-a}{2}dy \\
&\approx \sum_{i=1}^N \left(\frac{b-a}{2}\omega_i\right) f(\frac{b-a}{2}x+\frac{b+a}{2}) \\
&= \sum_{i=1}^N \omega_i’ f(x_i’)
\end{align}
\)
と掛けます。これをプログラムします。
ここでは、積分
\(
\displaystyle \int_{1}^{2.4}e^{-x} dx = e^{-1}-e^{-2.4} \approx 0.27716148788202981
\)
を計算します。

program main
  implicit none
  integer::i,N
  double precision,allocatable::x(:),w(:)
  double precision::f,s
  external::f
 
  N=15
  allocate(x(1:N),w(1:N)); x=0d0; w=0d0
  call GaussKronrod15ab(1d0,2.4d0,x,w)
  s=0d0
  do i=1,N
     s=s+w(i)*f(x(i))
  enddo  
  write(6,*)s

  deallocate(x,w)  
 
  stop
end program main

function f(x)
  implicit none
  double precision,intent(in)::x
  double precision::f
 
  f=exp(-x)

  return
end function f

subroutine GaussKronrod15ab(a,b,x,w)
  !Gauss-Kronrod Quadrature Nodes and Weights
  !http://www.advanpix.com/2011/11/07/gauss-kronrod-quadrature-nodes-weights/
  implicit none
  double precision,intent(in)::a,b
  double precision,intent(out)::x(1:15),w(1:15)
 
  integer::i
  integer,parameter::N=15
 
  x=0d0; w=0d0
 
  x( 8) = 0d0
  x( 9) = 2.077849550078984676006894037732449d-1
  x(10) = 4.058451513773971669066064120769615d-1
  x(11) = 5.860872354676911302941448382587296d-1
  x(12) = 7.415311855993944398638647732807884d-1
  x(13) = 8.648644233597690727897127886409262d-1
  x(14) = 9.491079123427585245261896840478513d-1
  x(15) = 9.914553711208126392068546975263285d-1  
  do i=1,7
     x(i)=-x(N-i+1)
  enddo
 
  w( 8) = 2.094821410847278280129991748917143d-1
  w( 9) = 2.044329400752988924141619992346491d-1
  w(10) = 1.903505780647854099132564024210137d-1
  w(11) = 1.690047266392679028265834265985503d-1
  w(12) = 1.406532597155259187451895905102379d-1
  w(13) = 1.047900103222501838398763225415180d-1
  w(14) = 6.309209262997855329070066318920429d-2
  w(15) = 2.293532201052922496373200805896959d-2
  do i=1,7
     w(i)=w(N-i+1)
  enddo
 
  x=0.5d0*((b-a)*x+(a+b))
  w=0.5d0*(b-a)*w
 
  return
end subroutine GaussKronrod15ab

となります。

実行結果は
0.277161487882030
となり、厳密値
0.27716148788202981
と全桁一致します。数値計算なので、最後のところは四捨五入されています。

61次ガウス=クロンロッド求積法

61次ガウス=クロンロッド求積法のコードも置いておきます。
これほどの高次は余り使わず、低次のものを組み合わせたほうが良いことを再び書いておきます。

積分
\(
\displaystyle \int_{-3}^{20}e^{-x} dx = e^{3}-e^{-20} \approx 20.0855369211265141
\)
を計算します。

program main
  implicit none
  integer::i,N
  double precision,allocatable::x(:),w(:)
  double precision::f,s
  external::f
 
  N=61
  allocate(x(1:N),w(1:N)); x=0d0; w=0d0
  call GaussKronrod61ab(-3d0,20d0,x,w)
  s=0d0
  do i=1,N
     s=s+w(i)*f(x(i))
  enddo  
  write(6,*)s

  deallocate(x,w)  
 
  stop
end program main

function f(x)
  implicit none
  double precision,intent(in)::x
  double precision::f
 
  f=exp(-x)

  return
end function f

subroutine GaussKronrod61ab(a,b,x,w)
  !Gauss-Kronrod Quadrature Nodes and Weights
  !http://www.advanpix.com/2011/11/07/gauss-kronrod-quadrature-nodes-weights/
  implicit none
  double precision,intent(in)::a,b
  double precision,intent(out)::x(1:61),w(1:61)
 
  integer::i
  integer,parameter::N=61
 
  x=0d0; w=0d0
 
  x(31:61) = &
       (/0.000000000000000000000000000000000d0  &
       , 5.147184255531769583302521316672257d-2 &
       , 1.028069379667370301470967513180006d-1 &
       , 1.538699136085835469637946727432559d-1 &
       , 2.045251166823098914389576710020247d-1 &
       , 2.546369261678898464398051298178051d-1 &
       , 3.040732022736250773726771071992566d-1 &
       , 3.527047255308781134710372070893739d-1 &
       , 4.004012548303943925354762115426606d-1 &
       , 4.470337695380891767806099003228540d-1 &
       , 4.924804678617785749936930612077088d-1 &
       , 5.366241481420198992641697933110728d-1 &
       , 5.793452358263616917560249321725405d-1 &
       , 6.205261829892428611404775564311893d-1 &
       , 6.600610641266269613700536681492708d-1 &
       , 6.978504947933157969322923880266401d-1 &
       , 7.337900624532268047261711313695276d-1 &
       , 7.677774321048261949179773409745031d-1 &
       , 7.997278358218390830136689423226832d-1 &
       , 8.295657623827683974428981197325019d-1 &
       , 8.572052335460610989586585106589439d-1 &
       , 8.825605357920526815431164625302256d-1 &
       , 9.055733076999077985465225589259583d-1 &
       , 9.262000474292743258793242770804740d-1 &
       , 9.443744447485599794158313240374391d-1 &
       , 9.600218649683075122168710255817977d-1 &
       , 9.731163225011262683746938684237069d-1 &
       , 9.836681232797472099700325816056628d-1 &
       , 9.916309968704045948586283661094857d-1 &
       , 9.968934840746495402716300509186953d-1 &
       , 9.994844100504906375713258957058108d-1 /)

  do i=1,30
     x(i)=-x(N-i+1)
  enddo
  w(31:61)= &
       (/5.149472942945156755834043364709931d-2 &
       , 5.142612853745902593386287921578126d-2 &
       , 5.122154784925877217065628260494421d-2 &
       , 5.088179589874960649229747304980469d-2 &
       , 5.040592140278234684089308565358503d-2 &
       , 4.979568342707420635781156937994233d-2 &
       , 4.905543455502977888752816536723817d-2 &
       , 4.818586175708712914077949229830459d-2 &
       , 4.718554656929915394526147818109949d-2 &
       , 4.605923827100698811627173555937358d-2 &
       , 4.481480013316266319235555161672324d-2 &
       , 4.345253970135606931683172811707326d-2 &
       , 4.196981021516424614714754128596976d-2 &
       , 4.037453895153595911199527975246811d-2 &
       , 3.867894562472759295034865153228105d-2 &
       , 3.688236465182122922391106561713597d-2 &
       , 3.497933802806002413749967073146788d-2 &
       , 3.298144705748372603181419101685393d-2 &
       , 3.090725756238776247288425294309227d-2 &
       , 2.875404876504129284397878535433421d-2 &
       , 2.650995488233310161060170933507541d-2 &
       , 2.419116207808060136568637072523203d-2 &
       , 2.182803582160919229716748573833899d-2 &
       , 1.941414119394238117340895105012846d-2 &
       , 1.692088918905327262757228942032209d-2 &
       , 1.436972950704580481245143244358001d-2 &
       , 1.182301525349634174223289885325059d-2 &
       , 9.273279659517763428441146892024360d-3 &
       , 6.630703915931292173319826369750168d-3 &
       , 3.890461127099884051267201844515503d-3 &
       , 1.389013698677007624551591226759700d-3/)
  do i=1,30
     w(i)=w(N-i+1)
  enddo
 
  x=0.5d0*((b-a)*x+(a+b))
  w=0.5d0*(b-a)*w
 
  return
end subroutine GaussKronrod61ab

実行結果
20.0855369211265
厳密値
20.0855369211265141

[adsense2]

fortran90で、任意の次数の求積点を知りたければ、f90のプログラムが
KRONROD Gauss-Kronrod Quadrature Rules -Source Codes in
Fortran90
にて公開されています。

参考文献

Gauss-Kronrod Quadrature Nodes and Weights

プログラミングと数値計算

unformattedによるファイル入出力(fortran90)

コメントする

fortran90でファイルの入出力に関する設定です。

fortranでデータの書き出しには、
書式付きと書式なしがあります。

書式付きはそこでプログラムがすべて終わる時
書式なしはそのデータを使って別のプログラムを動かす時
と使い分けられると思います。

[adsense1]

書式付き

利点
・テキストデータなので、結果を人間がわかりやすい形で出力出来る。
・ミスを発見しやすい
欠点
・データの書き出しに時間がかかる
・データ量が多くなる(書式なしの約3倍)

書式付きは、例えば

open(10,file="test.d")
write(10,'(A,i5,e15.5e2)')"aaa",j,alpha

見たいに書式を指定して書ださせることです。

書式なし

利点
・書き出し時間を短くできる
・データ量が少なくなる(書式付の約1/3倍)
・簡潔にコードが書ける
欠点
・バイナリファイルなので出力結果を直接見ることが出来ない。

書式なしのプログラムでは、

open(10,file="test.bin",form="unformatted")
write(10)"aaa",j,alpha

の様に書きます。

実際のプログラムでは、

program main
  implicit none
  integer,parameter::N1=4
  integer,parameter::N2=7

  integer::i,j
  double precision::A(1:N1),B(1:N2)
  complex(kind(0d0))::CC(1:N1,1:N2)
 
  do i=1,N1
     A(i)=100d0+dble(i)
  enddo
  do j=1,N2
     B(j)=dble(j)
  enddo
  do i=1,N1
     do j=1,N2
        CC(i,j)=A(i)+B(j)
     enddo
  enddo
     
!q  open(21,file="unformatted.bin",form="unformatted")
!q  write(21)N1,N2
!q  do i=1,N1
!q     do j=1,N2
!q        write(21)A(i),B(j),CC(i,j)
!q     enddo
!q  enddo
!q  close(21)

  open(21,file="unformatted.bin",form="unformatted")
  write(21)N1,N2
  write(21)A,B,CC
  close(21)
 
  stop
end program main

といった感じです。

書式なしの読み込み

書式なしのファイルを読み込むためにはまったく同じ形で読み込ませればいいです。
例えば、上の形で書いた場合、読み込みは

program main
  implicit none
  integer::i,j,N1,N2
 
  double precision,allocatable::A(:),B(:)
  complex(kind(0d0)),allocatable::CC(:,:)
 
  open(21,file="unformatted.bin",form="unformatted")
  read(21)N1,N2
  allocate(A(1:N1),B(1:N2),CC(1:N1,1:N2))
!q  do i=1,N1
!q     do j=1,N2
!q        read(21) A(i),B(j),CC(i,j)
!q     enddo
!q  enddo
  read(21) A,B,CC
  close(21)
 
  do i=1,N1
     do j=1,N2
        write(6,'(4f10.5)')A(i),B(j),CC(i,j)
     enddo
  enddo
 
  stop
end program main

とすればいいです。
”!q”のコメントアウトは２つのプログラムに共通しています。
なのでどういう書き方でも、同じ入出力の形を指定してあげれば良いです。

[adsense2]

弾道計算

BB弾の回転量について(実験との比較)

2件のコメント

BB弾の回転量について,係数\(C_l\)は
\(
\begin{align}
C_l&\approx 0.12\\
\end{align}
\)
で近似できる、と実験データから求まりました。
実験データ(ハイスピードカメラによる回転量計測及び弾道データ)を提供してくださった
ガンジニア、石岡様(http://gungineer.matrix.jp/)に感謝いたします。

弾道計算に関するその他ページ
弾道計算(BB弾)の理論
BB弾の回転量について(実験との比較)←今ここ
弾道計算(BB弾)の結果
弾道計算の結果2, 比較と詳細データ
弾道計算(BB弾)のコード(fortran90)
バレル内部でのBB弾の方程式

[adsense1]

対象とする問題

BB弾の運動方程式を求める事が出来ましたが、BB弾の回転量に関して計算と実験との間に4~5倍近い差が生じていました。この原因は、BB弾の回転量と発生する循環を一緒にしていたためです。式で表せば運動方程式は

・BB弾の運動方程式
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}+\left\{-6\pi \eta R |\vec{V}|-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|^2\right\}\frac{\vec{V}}{|\vec{V}|}
-C_l\left(S_p\right)\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
・BB弾の回転角速度の減衰を記述する方程式
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)

と書けます。今まで係数\(C_l\left(S_p\right)\)を1にしていました。
この係数を求める事が今回の目標です。

良く使われるパラメータにスピンパラメータ\(S_p\)なるものが存在するようで[1]、今回はこれに倣います。
これは回転球の表面での速度\(R\omega\)と飛翔速度\(v\)に関する無次元量で,
\(
S_p=R\omega/v
\)
と書かれます。
BB弾の場合、実験[2]より、おおよそ150[回転/秒, rps]ということが分かりました。
飛翔速度はおおよそ\(80[{\rm m/s}]\)と考えると、スピンパラメータの値の範囲はおおよそ
\(
\displaystyle S_p=\frac{3\times 10^{-3}{\rm [m]}\cdot 2\pi\cdot 150{\rm [/s]}}{80{\rm [m/s]}}\sim 0.0353\cdots
\)
という量になります。よって、\(C_l(S_p)\)を\(S_p=0\)回りでテーラー展開して、
\(
C_l(S_p)\sim c_0+c_1 S_p+c_2 S_p^2 +O(S_p^3)
\)
と考えられます(補足1)。

\(C_l(S_p)\)の導出

係数\(C_l(S_p)\)を以下のように求めます。

・ある既知の回転量で射出されたBB弾が描く軌道
と
・その既知の回転量を初期条件として運動方程式を解いた場合の軌道

の分散を最小にするパラメータをモンテカルロ法によって求めます。モンテカルロ法などと言っていますが、これは\(c_0,c_1\)に乱数を適当に振って良さげなものを求める、ということです。

ここでは実験から得られたある3つの回転量
case1：117回転/秒
case2：147回転/秒
case3：191回転/秒
の軌道との比較を行います。

実験のデータ点\(x_i\)と数値計算でのデータ点\(X_i\)との差の2乗の平方根をデータ点数\(N\)で割ったものを\(\Delta\)と定義します。

この\(\Delta\)が最も小さくなるパラメータの組み合わせが今求めたいものです。
縦軸に\(\Delta\)、横軸に各々のパラメータ\(c_0,c_1,c_2\)を取ったものをグラフにすると以下のようになります。
Delta_param2

各々のcase1,case2,case3で、\(\Delta\)を最小にするパラメータで軌道と終端速度の妥当性を見てみますとこうなります。

velocity_expthe5

速度が合わない原因としては恐らく、終端速度の計測機器による不具合でしょう。

なぜなら、初期速度を実験から得られたデータ値にした際、case3に対して同様にフィッティングするとばらつき具合を示す\(\Delta\)が1.9という値になってしまい、明らかに悪くなるからです。

実験のデータ点に+3[m/s]にするとおおよそ妥当なことが分かります。
velocity_expthe3
きっと計測機器の初期値がずれていただけでしょう。

\(\Delta\)の図から、最小地点3点での平均を取ればいいです。すると
\(
c_0\approx 0.18,\;\;\; c_1\approx -1.4 \;\; c_2=?
\)
と求める事が出来ました。\(c_2\)の項が求まりませんでしたので、\(c_1\)で打ち切ります。

考察

\(c_1\)で打ち切ることを考えると少し問題が生じます。今、\(c_1\)はどうやら負のようです。
と言うことは、これをこのまま高速回転する状況に使うと、回転が増えると逆に落ちやすくなる事を意味しています。\(S_p\)が上のように限定されている場合では精度よく求められますが、広い範囲ではちょっと上の級数展開式は使えません。

現実的な問題で考えましょう。
物理的に正しくなるように、係数\(C_l(S_p)\)は常に正の値でなければならないと仮定します。なので、上の級数展開はよろしくありません。
単純に定数として求めてしまいましょう。すなわち、
\(
\begin{align}
C_l(S_p)&\approx c_0
\end{align}
\)
とします。球自体の循環だけに依存するとして広い範囲で(とりあえず)使える定数を求めます。
Delta_param_const2
そうして実験データから\(\Delta\)を最小にする\(c_0\)を求めてやると、
\(
C_0=0.12
\)
と求まりました。
実際に\(C_l(S_p)=0.12\)で実験との比較をしてみますと、こうなります。
constcl012_c
定数として考えてもそんなに悪くないと思います。
case1,case3 を用いて、\(C_l(S_p)=0.12\)の妥当性を考えてみます。
\(C_l=0.12\)として、大体どの程度の回転量の誤差に収まっているかを示したのが以下の図です。
click1020pm20
数値計算上で求められた回転量は現実の回転量と10%程度の誤差に収まっていることが分かりました。

どれが良いかは一概には言えません。
回転量を知らなくていいなら\(C_l(S_p)=1\)で良いと思います。
回転数を大雑把にでも知りたければ\(C_l(S_p)=0.12\)を、
\(S_p\)が小さい、すなわちホップをあまりかけないで0.9J近くで飛ばす限定された状況では\(C_l(S_p)= 0.18-1.4S_p\)が良いと思います。

[adsense2]

結論

エアガンから射出された、BB弾の従う方程式は

・BB弾の運動方程式
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|^2\frac{\vec{V}}{|\vec{V}|}
-C_l\left(S_p\right)\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
・BB弾の回転角速度の減衰を記述する方程式
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)
ここで、
\(
\begin{align}
&C_l(S_p)\sim 0.18-1.4S_p+O(S_p^2) \\
&S_p=R\omega/v
\end{align}
\)
もしくは
\(
C_l(S_p)\sim 0.12
\)
で近似できる。
という結論を得ました。

最後に、実験データ(ハイスピードカメラによる回転量計測[2]及び弾道データと速度データ)を提供してくださった
ガンジニア、石岡大樹様(http://gungineer.matrix.jp/)に心より感謝申し上げます。
以下の実験時の条件は石岡様が行っていただいた条件です。

実験[2]とデータ採取時の条件

エアガン：東京マルイ　VSR-10 G-SPEC
BB弾：ギャロップ 0.3g
ハイスピードカメラ：PHOTRON MH4-10K、10000fps
データ点の採取方法：Stealth-Target ST17

室温、湿度、気圧の計測
1つのデータ点につき、30回計測

補足1

私の予測ですが、\(C_l\)の展開方法について述べておきます。
論文[1]によると、回転による揚力を私のようには書いておらず、
揚力を\(L\)と記述し、
\(
\displaystyle L=\frac{1}{2}C_l\rho U^2 A
\)
のように記述しています。ここで、\(\rho\)は空気の密度、\(U\)は球の速度、\(A\)は球の直径断面積です。
[1]では\(L\)を実験から直接求めて\(C_l\)を求めています。
この時に\(C_l\)をスピンパラメータ\(S_p\)で展開して実験データをフィッティングしているので私の計算と事情が違うのかもしれません。

[1]を頼らないことにしましょう。
物理的な予測から求めていきます。回転量依存だと考え、\(C_l(\omega)\)として考えます。
１．どんな回転量でも\(C_l\)は正である必要があります(負のマグヌス力は今回の場合発生しないと考える)。なので、
\(
C_l(\omega) > 0
\)
でなければなりません。
２．回転が非常に0に近い時、球体の循環と周りで発生する循環は一致するはずです。
なので、
\(
C_l(\omega\to 0)=1
\)
であることが予想されます。
３．回転が非常に強い場合、周辺の空気は限られるため発生する揚力は弱くなっていくはずです。
ただし、回転が無限大の時、揚力自体は発散すると予想できるので、係数\(C_L\)は揚力の発散を抑えてはなりません。なので、
\(
C_l(\omega\to\infty) = A\omega^{k},\;\;(A=\mbox{const},\;\; -1 \lt k )
\)
であるはずです。

物理的な考察から、係数\(C_l\)が満たすべき条件はこんなものでしょうか。
BB弾の回転量\(\omega\)が程々の場合は予想が出来ません。どこかにピークがあるのかもしれませんし、緩やかに減少していくだけかもしれません。
適当な関数を持ってくるのも手ですが、私は嫌います。
そんなことをやるのなら定数でいいだろうとして、
\(C_l=0.12\)と言う結論となりました。

参考文献

[1]鳴尾 丈司, 溝田 武人, 下園 仁志, “一様気流中で高速回転するゴルフボールの空気力測定と飛しょう実験” 日本機械学会論文集 B編 Vol. 70 (2004) No. 697 P 2371-2377
[2]石岡大樹、ホップアップの回転数測定　TM VSR-10 G-SPEC

プログラミングと数値計算, 数学

ディガンマ関数の数値計算

4件のコメント

ディガンマ関数\(\psi(z)\)は

\(
\displaystyle \psi(z)=\frac{d}{dz} \ln\Gamma(z)=\frac{\Gamma'(z)}{\Gamma(z)}
\)
として定義されます。

数値計算でこれを求めます。
用いる式は、
ディガンマ関数の漸近展開式[1],
\(
\displaystyle \psi(z)\sim \ln z -\frac{1}{2z}-\sum_{n=1}^{\infty} \frac{B_{2n}}{2nz^{2n}},\;\; z\to\infty (|{\rm arg} z| \lt \pi )
\)
ここで\(B_{2n}\)はベルヌーイ数[2]
と
漸化式[1]
\(
\displaystyle \psi(z+1)=\psi(z)+\frac{1}{z}
\)
相反公式[1]
\(
\psi(1-z)=\psi(z)+\pi \cot(\pi z)
\)
を利用します。

具体的には領域を4つに分けて、

  1. \(10 \lt {\rm Re}(z)\),      漸近展開
  2. \(1 \lt {\rm Re}(z) \lt 10\),    漸近展開+漸化式
  3. \(-9 \lt {\rm Re}(z) \lt 1\),    漸近展開+漸化式+相反公式
  4. \({\rm Re}(z) \lt -9\),      漸近展開+相反公式

を利用しています。

program main
  implicit none
  integer::i,j
  double precision::x,y
  complex(kind(0d0))::z,digamma
  external::digamma
 
  do i=0,200
     x=-10.05d0+i*0.1d0
     do j=0,200
        y=-10.05d0+j*0.1d0
        z=dcmplx(x,y)
        write(10,'(4e20.10e2)')x,y,dble(digamma(z)),dimag(digamma(z))
     enddo
     write(10,*)
  enddo
 
  stop
end program main

!--------------------------

function digamma(z)
  ! digamma function for complex plane
  ! sikinote, http://slpr.sakura.ne.jp/qp/
  ! author : sikino
  ! date : 2016/07/04 (yyyy/mm/dd)
  ! date : 2016/07/07 (yyyy/mm/dd)
  implicit none
  complex(kind(0d0)),intent(in)::z
  complex(kind(0d0))::digamma
 
  integer::i,j,n,m,as,key
  integer,parameter::nmax=100
  double precision::eps=1d-13
  double precision::pi=4d0*atan(1d0)
  complex(kind(0d0))::c,w,t,ds,s
  double precision::B
  external::B

  as=10

  if(dble(z).ge.dble(as))then
     w=z
     key=0
  elseif(dble(z).ge.1d0)then
     w=z+dble(as)
     key=1
  elseif(dble(z).ge.-dble(as-1))then
     w=1d0-z+dble(as)
     key=2
  else
     w=1d0-z
     key=3
  endif
 
  ! Asymptotic expansion
  s=log(w)-0.5d0/w
  do n=1,nmax
     m=2*n
     ds=B(m)/(m*w**m)
     s=s-ds
     if(abs(ds)/abs(s).le.eps)exit
  enddo
  if(n.eq.nmax+1)then
     write(6,*)"Worning! did not converge at digamma"
  endif
 
  if(key.eq.1.or.key.eq.2)then
     !Recurrence relation
     do i=1,as
        s=s+1d0/(1d0-w)
        w=w-1d0
     enddo
  endif
  if(key.eq.2.or.key.eq.3)then
     ! Reflection Formula
     s=s-pi/tan(pi*z)
  endif

  digamma=s
 
  return
end function digamma
!--------------------------
function B(n)
  ! 1st bernoulli number B(n), 0 <= n <= 100
  ! from wolfram alpha
  !    " Table[bernoulli b(i), {i,0,100}] with 17 digits "
  implicit none
  integer,intent(in)::n
  double precision::B,A(0:100)
 
  if(n.lt.0.or.n.gt.100)then
     write(6,*)"Not expected n at bernoulli number function. "
     write(6,*)"program stop"
     stop
  endif
 
  A(0:100)=(/1d0 &
       ,  -0.50000000000000000d0, 0.16666666666666667d0, 0d0, -0.033333333333333333d0, 0d0 &
       ,  0.023809523809523810d0, 0d0, -0.033333333333333333d0, 0d0,  0.075757575757575758d0, 0d0 &
       ,  -0.25311355311355311d0, 0d0,    1.1666666666666667d0, 0d0,   -7.0921568627450980d0, 0d0 &
       ,    54.971177944862155d0, 0d0,   -529.12424242424242d0, 0d0,    6192.1231884057971d0, 0d0 &
       ,   -86580.253113553114d0, 0d0,   1.4255171666666667d+6, 0d0,  -2.7298231067816092d+7, 0d0 &
       ,   6.0158087390064237d+8, 0d0, -1.5116315767092157d+10, 0d0,  4.2961464306116667d+11, 0d0 &
       , -1.3711655205088333d+13, 0d0,  4.8833231897359317d+14, 0d0, -1.9296579341940068d+16, 0d0 &
       ,  8.4169304757368262d+17, 0d0, -4.0338071854059455d+19, 0d0,  2.1150748638081992d+21, 0d0 &
       , -1.2086626522296526d+23, 0d0,  7.5008667460769644d+24, 0d0, -5.0387781014810689d+26, 0d0 &
       ,  3.6528776484818123d+28, 0d0, -2.8498769302450882d+30, 0d0,  2.3865427499683628d+32, 0d0 &
       , -2.1399949257225334d+34, 0d0,  2.0500975723478098d+36, 0d0, -2.0938005911346378d+38, 0d0 &
       ,  2.2752696488463516d+40, 0d0, -2.6257710286239576d+42, 0d0,  3.2125082102718033d+44, 0d0 &
       , -4.1598278166794711d+46, 0d0,  5.6920695482035280d+48, 0d0, -8.2183629419784576d+50, 0d0 &
       ,  1.2502904327166993d+53, 0d0, -2.0015583233248370d+55, 0d0,  3.3674982915364374d+57, 0d0 &
       , -5.9470970503135448d+59, 0d0,  1.1011910323627978d+62, 0d0, -2.1355259545253501d+64, 0d0 &
       ,  4.3328896986641192d+66, 0d0, -9.1885528241669328d+68, 0d0,  2.0346896776329074d+71, 0d0 &
       , -4.7003833958035731d+73, 0d0,  1.1318043445484249d+76, 0d0, -2.8382249570693707d+78/)
 
  B=A(n)
 
  return
end function B

[adsense2]

参考文献

[1]Abramowitz, M. and I.A. Stegun, {\it Handbook of Mathematical Functions}, Dover Publications, Ninth Printing, 1970., P.258-259, Eq.6.3.18(漸近展開式), Eq.6.3.5(漸化式), Eq.6.3.7(相反公式)
[2]Bernoulli Number -wolfram mathworld

プログラミングと数値計算, 数学

ベルヌーイ数の数値計算

コメントする

これがベルヌーイ数を求める最速のアルゴリズムだと思います。
直接代入。これに限ります。

n=0~100までサポートしています。
実用的にはこの範囲で足りるんじゃないかなと思います。

値はwolfram alphaより。
Table[bernoulli b(i), {i,0,100}] with 17 digits

program main
  implicit none
  integer::i
  double precision::B
  external::B
 
  do i=0,30
     write(6,'(i5,f30.17)')i,B(i)
  enddo
 
  stop
end program main
   
function B(n)
  ! 1st bernoulli number B(n), 0 <= n <= 100
  ! from wolfram alpha
  !    " Table[bernoulli b(i), {i,0,100}] with 17 digits "
  implicit none
  integer,intent(in)::n
  double precision::B
  double precision::A(0:100)
 
  if(n.lt.0.or.n.gt.100)then
     write(6,*)"Not expected n at bernoulli number function. "
     write(6,*)"program stop"
     stop
  endif
   
  A(0:100)=(/1d0 &
       ,  -0.50000000000000000d0, 0.16666666666666667d0, 0d0, -0.033333333333333333d0, 0d0 &
       ,  0.023809523809523810d0, 0d0, -0.033333333333333333d0, 0d0,  0.075757575757575758d0, 0d0 &
       ,  -0.25311355311355311d0, 0d0,    1.1666666666666667d0, 0d0,   -7.0921568627450980d0, 0d0 &
       ,    54.971177944862155d0, 0d0,   -529.12424242424242d0, 0d0,    6192.1231884057971d0, 0d0 &
       ,   -86580.253113553114d0, 0d0,   1.4255171666666667d+6, 0d0,  -2.7298231067816092d+7, 0d0 &
       ,   6.0158087390064237d+8, 0d0, -1.5116315767092157d+10, 0d0,  4.2961464306116667d+11, 0d0 &
       , -1.3711655205088333d+13, 0d0,  4.8833231897359317d+14, 0d0, -1.9296579341940068d+16, 0d0 &
       ,  8.4169304757368262d+17, 0d0, -4.0338071854059455d+19, 0d0,  2.1150748638081992d+21, 0d0 &
       , -1.2086626522296526d+23, 0d0,  7.5008667460769644d+24, 0d0, -5.0387781014810689d+26, 0d0 &
       ,  3.6528776484818123d+28, 0d0, -2.8498769302450882d+30, 0d0,  2.3865427499683628d+32, 0d0 &
       , -2.1399949257225334d+34, 0d0,  2.0500975723478098d+36, 0d0, -2.0938005911346378d+38, 0d0 &
       ,  2.2752696488463516d+40, 0d0, -2.6257710286239576d+42, 0d0,  3.2125082102718033d+44, 0d0 &
       , -4.1598278166794711d+46, 0d0,  5.6920695482035280d+48, 0d0, -8.2183629419784576d+50, 0d0 &
       ,  1.2502904327166993d+53, 0d0, -2.0015583233248370d+55, 0d0,  3.3674982915364374d+57, 0d0 &
       , -5.9470970503135448d+59, 0d0,  1.1011910323627978d+62, 0d0, -2.1355259545253501d+64, 0d0 &
       ,  4.3328896986641192d+66, 0d0, -9.1885528241669328d+68, 0d0,  2.0346896776329074d+71, 0d0 &
       , -4.7003833958035731d+73, 0d0,  1.1318043445484249d+76, 0d0, -2.8382249570693707d+78/)
 
  B=A(n)
 
  return
end function B

B(256)まで増やしたのはこちら。

一応逐次的に求める事が出来るアルゴリズムがありまして実装しましたが、全然良くないです[1]。
4倍精度演算を使って\(B_{30}\)を求めようとするとたったの8桁しか一致しません。
倍精度演算のみだと\(B_{14}\)を求めようとするとたったの6桁しか一致しません。

参考文献

[1]Algorithmic description -Bernoulli number, wikipedia

[adsense2]