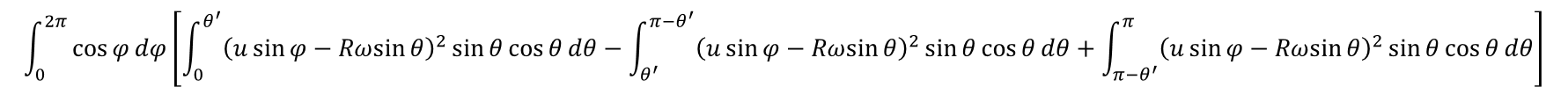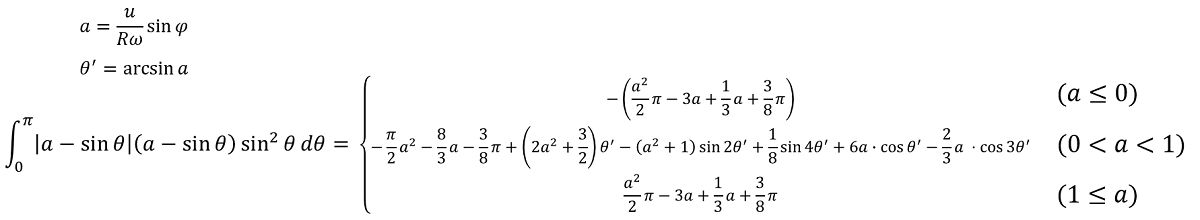月別アーカイブ: 2015年1月

プログラミングと数値計算

プリクラ問題

コメントする

covering designのt=2に相当、
La Jolla Covering Repository Tablesに全部載ってます…
リンク先クリックすればいいんだね。
Combinatorial covering designs に文献とかあるから、なんかもう・・・
もういいや

fortran90によるのコードはこのページの下の方です
だんだんと条件を付け加えて更新していくつもりです。n=9~10でm=3,4程度は厳しいです。

力技でやってみたよ!
主眼が回数になっているので、実際の組み合わせは？と気になってやったものです。

事の発端

コンピュータによる総当たりでは今のままではn=10位が限界です。
だんだんと改良して増やせていければ、と。
コードは後ほど僕に時間ができ次第、公開します。


より↓

念のための確認もかねて、計算は表の値-1から確かめて総当たりを行った結果です。なので具体的な組み合わせが載っているものは正しいはずです。
組み合わせの総数はおおよそ
\(\displaystyle \sum_{q=3}^{q^{Answer}} {}_{{}_nC_m}C_{q}\)
という膨大な数の組み合わせとなります。ここで\(q^{Answer}\)はプリクラ問題の最小回数です。
\(q=3\)はあり得ない、全てを検証する必要はない、など確実にわかる要素は多いですが、例えばn=9,m=3,解q=12を考えると
\(\displaystyle {}_{{}_9C_3}C_{12}=112,992,892,764,570 \ \ \sim 10^{14}(=100T)\)回
の計算が必要です。理想的な状況を考え、cpu10GHz,コア数10で並列処理で行う場合、計算時間は
\(\displaystyle \frac{10^{14}回}{10\times 10^{9}Hz\cdot 10\mbox{コア}}=1000[秒]\)
なのでぎりぎり計算できそうかなーくらいになります。
しかし、このあたりが限界で、n=10,m=3,解q=17になると、
\(\displaystyle {}_{{}_{10}C_3}C_{17}=189,916,591,435,396,829,640\ \ \sim 10^{20}(100E)\)回
の計算となります。先ほどの設定で行うならば、\(10^{9}\)秒~31.7年かかります。
スパコンの京(10PHz)をフルに使えるならば1000[s]で終わります。しかしそこで終わりです。n=11は…もう無理です。

効率のいい方法を考えない限り、解は得られません。

n\m 2 3 4 5 6 7 8 9 10 11
2 1 1 1 1 1 1 1 1 1 1
3 3 1 1 1 1 1 1 1 1 1
4 6 3 1 1 1 1 1 1 1 1
5 10 4 3 1 1 1 1 1 1 1
6 15 6 3 3 1 1 1 1 1 1
7 21 7 5 3 3 1 1 1 1 1
8 28 11 6 4 3 3 1 1 1 1
9 36 12 8 5 3 3 3 1 1 1
10 45 17 9 6 4 3 3 3 1 1
11 55 19 11 7 6 4 3 3 3 1

(3,2)=3

1 2
1 3
2 3

(4,2)=6

略

(4,3)=3

1 2 3
1 2 4
1 3 4

(5,2)=10

略

(5,3)=4

1 2 3
1 2 4
1 2 5
3 4 5

(5,4)=3

1 2 3 4
1 2 3 5
1 2 4 5

(6,2)=15

略

(6,3)=6

1 2 3
1 2 4
1 5 6
2 5 6
3 4 5
3 4 6

(6,4)=3

1 2 3 4
1 2 5 6
3 4 5 6

(6,5)=3

1 2 3 4 5
1 2 3 4 6
1 2 3 5 6

(7,2)=21

略

(7,3)=7

1 2 3
1 4 5
1 6 7
2 4 6
2 5 7
3 4 7
3 5 6

(7,4)=5

1 2 3 4
1 2 3 5
1 2 3 6
1 2 3 7
4 5 6 7
or
1 2 3 5
1 4 6 7
2 3 4 5
2 4 6 7
3 5 6 7

(7,5)=3

1 2 3 4 5
1 2 3 6 7
1 4 5 6 7

(7,6)=3

1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7

(8,2)=28

略

(8,3)=11

計算中…

(8,4)=6

1 2 3 4
1 2 5 6
1 2 7 8
3 4 5 6
3 4 7 8
5 6 7 8

(8,5)=4

1 2 3 4 5
1 2 3 4 6
1 2 3 7 8
4 5 6 7 8

(8,6)=3

1 2 3 4 5 6
1 2 3 4 7 8
1 2 5 6 7 8

(8,7)=3

1 2 3 4 5 6 7
1 2 3 4 5 6 8
1 2 3 4 5 7 8

(9,2)=36

略

(9,3)=12

計算中…

(9,4)=8

1 2 3 5
1 2 3 6
1 2 4 7
1 2 8 9
1 3 4 8
1 3 7 9
4 5 6 9
5 6 7 8


info)cputime=3.0415[s], Nc=10523209, com=1 2 35 115 126

(9,5)=5

1 2 3 4 5
1 2 3 4 6
1 2 7 8 9
3 4 7 8 9
5 6 7 8 9

(9,6)=3

1 2 3 4 5 6
1 2 3 7 8 9
4 5 6 7 8 9

(9,7)=3

1 2 3 4 5 6 7
1 2 3 4 5 8 9
1 2 3 6 7 8 9

(9,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 9
1 2 3 4 5 6 8 9

(10,2)=45

略

(10,3)=17

計算厳しい

(10,4)=9

計算中(4日後くらい?)

(10,5)=6

(10,6)=4

1 2 3 4 5 6
1 2 3 4 7 8
1 2 3 4 9 10
5 6 7 8 9 10

(10,7)=3

1 2 3 4 5 6 7
1 2 3 4 8 9 10
1 5 6 7 8 9 10

(10,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 6 9 10
1 2 3 4 7 8 9 10

(10,9)=3

1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 10
1 2 3 4 5 6 7 9 10

(11,2)=55

略

(11,3)=19

(11,4)=11

(11,5)=7

(11,6)=

(11,7)=4

1 2 3 4 5 6 7
1 2 3 4 5 6 8
1 2 3 4 9 10 11
5 6 7 8 9 10 11

(11,8)=3

1 2 3 4 5 6 7 8
1 2 3 4 5 9 10 11
1 2 6 7 8 9 10 11

(11,9)=3

1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 10 11
1 2 3 4 5 8 9 10 11

(11,10)=3

1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 11
1 2 3 4 5 6 7 8 10 11


fortran90のコード。総当たりで調べます。
別にinputファイルが必要です。n:m=3:2以上の時は考慮していません。3回で終わるからね。
下の例はn=6, m=3に相当しています。(inputのrはmに相当します。)
qiは調べ始める最低回数、qeは調べ終わる最高回数です。
出力はこうなります。

 M          35
q  -->    3
q  -->    4
q  -->    5
q  -->    6
q  -->    7
 number of calculation     1276464
 cpu_time  0.905050993     [sec]
+------------+
  1  2  3
  1  4  5
  1  6  7
  2  4  6
  2  5  7
  3  4  7
  3  5  6
+------------+

ここからfortran90のコード。gfortranで確かめています。

program main
  implicit none
  integer::n,r,qi,qe,qc
  integer::i,j
  real::t1,t2
  integer,allocatable::groups(:,:)
 
  n=7
  r=3
  qi=3
  qe=10
  allocate(groups(1:qe,1:r))
  groups=0

  call cpu_time(t1)  
  call pkprob(n,r,qi,qe,qc,groups)
  call cpu_time(t2)
  write(6,*)"cpu_time",t2-t1,"[sec]"

  write(6,'(A)')"+------------+"
  do i=1,qc
     do j=1,r
        write(6,'(i3)',advance='no')groups(i,j)
     enddo
     write(6,*)          
  enddo
  write(6,'(A)')"+------------+"
 
  stop
end program main
!==========================
subroutine pkprob(n,r,qi,qe,qc,groups)
  !Covering Design t=2
  implicit none
  integer,intent(in)::n,r,qi,qe
  integer,intent(out)::qc,groups(1:qe,1:r)
 
  integer::q,M,ic,ncalc
  integer::i,j,q2,k
  integer,allocatable::ini(:),tmp(:),cgroup(:,:),pk(:,:)
  integer,allocatable::choose(:)
 
  integer::check1,nCr
  integer::csign
  !  logical::csign,gsign
  external::nCr

  !Combination M=nCr
  M=nCr(n,r)  
  write(6,*)"M",M

  !csign      : Sign of critical combination of array  
  !ic         : Critical value of i which number of combination of combination
  !qc         : Critical value of q which number of combination of combination
  !pk(1:n,1:n): Checking array if every number fill(1) combination or not(0)
  !ncount(1:n): To check calculation number of times
  allocate(ini(1:r),tmp(1:r),cgroup(1:M,1:r))
  ini(1:r)=0
  cgroup(1:M,1:r)=0
  tmp(1:r)=0
 
  do j=1,r
     ini(j)=j
     tmp(j)=ini(j)
  enddo
  !Substitute combination to cgroup.
  do i=1,M
     cgroup(i,1:r)=tmp(1:r)
     call combination(n,r,ini,tmp)
  enddo
  deallocate(ini,tmp)
  !csign      : Sign of critical combination of array  
  !ic         : Critical value of i which number of combination of combination
  !qc         : Critical value of q which number of combination of combination
  !pk(1:n,1:n): Checking array if every number fill(1) combination or not(0)
  !ncount(1:n): To check calculation number of times
  csign=0
  ic=0
  qc=0
  allocate(pk(1:n,1:n))
  pk=0

  ncalc=0

  !q : We need to consider below combination.
  !  Example ) n=5, r=3 case.
  !
  !cgroup(i,1:r)
  !i\r| 1 2 3
  !----------
  ! 1 | 1 2 3
  ! 2 | 1 2 4
  ! 3 | 1 2 5
  ! 4 | 1 3 4
  ! 5 | 1 3 5
  ! 6 | 1 4 5
  ! 7 | 2 3 4
  ! 8 | 2 3 5
  ! 9 | 2 4 5
  !10 | 3 4 5
  !
  !We have to choose q= 3 or 4 or 5 ...combination of "cgroup".
  !Sum total of these combination can write D=_{nCr}C_q.
  !Specifically,
  !---choose q groups from cgroup
  ! +----q=3----+ +-----q=4-----+ +------q=5------+
  ! |choose(1:q)| | choose(1:q) | |  choose(1:q)  |
  ! | l |       | | l |         | | l |           |
  ! |===|=======| |===|=========| |===|===========|
  ! | 1 | 1 2 3 | | 1 | 1 2 3 4 | | 1 | 1 2 3 4 5 |
  ! | 2 | 1 2 4 | | 2 | 1 2 3 5 | | 2 | 1 2 3 4 6 |
  ! | 3 | 1 2 5 | | 3 | 1 2 3 6 | | 3 | 1 2 3 4 7 |
  ! | 4 | 1 2 6 | | 4 | 1 2 4 7 | | 4 | 1 2 3 4 8 |
  ! | 5 | 1 2 7 | | 5 | 1 2 4 8 | | 5 | 1 2 3 4 9 |
  ! | 6 | 1 2 8 | | 6 | 1 2 5 9 | | 6 | 1 2 3 4 10|
  ! | 7 | 1 2 9 | | 7 | 1 2 5 10| | 7 | 1 2 3 5 6 |
  ! |...| . . . | |...| . . . . | |...| . . . .   |
  ! |120| 4 5 6 | |210| 7 8 9 10| |252| 6 7 8 9 10|
  ! +-----------+ +-------------+ +---------------+
  !
  ! If q=4, l=3
  !  We choose below combination, and check satisfy condition or not by "pk".
  ! 1 | 1 2 3
  ! 2 | 1 2 4
  ! 3 | 1 2 5
  ! 6 | 1 4 5
 
  do q=qi,qe
     write(6,'(A,i5)')"q  -->",q
     allocate(choose(1:q),ini(1:q))
     choose(1:q)=0
     ini(1:q)=0
     
     do j=1,q
        ini(j)=j
        choose(j)=ini(j)
     enddo
         
     csign=0
     do while(csign.eq.0)
        !condition 1 to reduce calculation
        check1=cgroup(choose(1),1)
        if(check1.ne.1)exit

        !condition 2 to reduce calculation
        check1=cgroup(choose(2),1)
        if(check1.ge.2)exit

        !condition 3 to reduce calculation for less than n:r=3:2
        check1=cgroup(choose(q),1)
        if(check1.ge.3)then
           pk=0
           do q2=1,q
              do j=1,r
                 do k=1,r
                    pk(cgroup(choose(q2),j),cgroup(choose(q2),k))=1
                 enddo
              enddo
           enddo
           !memory calculation number of times
           ncalc=ncalc+1
           if(minval(pk).eq.1)then
              csign=1
              qc=q
           endif

           if(csign.eq.1)exit
        endif

        !go forward choose(1:q)
        call combination(M,q,ini,choose)
     enddo
     
     if(csign.eq.1)exit
     deallocate(choose,ini)
  enddo
  write(6,*)"number of calculation",ncalc

  groups(1:qe,1:r)=0
  do i=1,qc
     do j=1,r
        groups(i,j)=cgroup(choose(i),j)
     enddo
  enddo
 
  return
end subroutine pkprob
!---------------------------------
subroutine combination(n,r,ini,arr)
  implicit none  
  integer(8)::i,n,r,ini(1:r),bef(1:r),arr(1:r)
  integer(8)::numx
  logical::key(1:r)
 
  bef(1:r)=arr(1:r)-ini(1:r)
  arr(1:r)=0
  key(1:r)=.false.

  numx=n-r
  do i=1,r
     if(bef(i).eq.numx)key(i)=.true.
  enddo

  do i=1,r-1
     if(key(i+1))then
        if(key(i))then
           if(i.ne.1)arr(i)=arr(i-1)      
        else
           arr(i)=bef(i)+1
        endif
     else
        arr(i)=bef(i)
     endif
  enddo
  if(key(r))then
     arr(r)=arr(r-1)
  else
     arr(r)=bef(r)+1
  endif
 
  arr(1:r)=arr(1:r)+ini(1:r)

  return
end subroutine combination
!----------------------------------
function nCr(n,r)
  implicit none
  integer(8)::n,r,i,r0,nCr

  r0=n-r
  if(r.le.r0)r0=r

  nCr=1
  do i=1,r0
     nCr=nCr*(n-r0+i)
     nCr=nCr/i
  enddo
 
  return
end function nCr
Linux

LXDE

1件のコメント

LinuxMint 17.1 “Rebecca” においてデスクトップ環境”lxde”をインストールするための手順です。

LXDEの導入

lxdeとは?
→Arch Linux LXDE (日本語)より引用

LXDE (“Lightweight X11 Desktop Environment”) は極めて高いパフォーマンスを持ち省エネルギーなデスクトップ環境です。開発者たちの国際的なコミュニティにより管理され、美しいインターフェース、多言語対応、標準的なキーボードショートカットとタブファイラーのような追加機能を含みます。LXDE は CPU も RAM も他のデスクトップ環境に比べ消費が少ないです。特に、ネットブック、モバイル端末や、古い計算機などによるクラウドコンピューティングにあわせてデザインされています。

ぶっちゃければ軽いよ！ということです。
windowsだったらこの変更に相当する操作はありません。
これからやろうとしているのは
OS → バージョン → デスクトップ環境
の順で書けば、
LinuxMint → 17.1(Rebecca) → cinnamon
から
LinuxMint → 17.1(Rebecca) → LXDE
に変更する、という操作です。cinnamon, LXDEの他にMate, KDE, Xfceなどがあります。
詳しくは調べてください。

設定→Synapticパッケージマネージャ
と進みます。
Synapticパッケージマネージャの検索ボックスでlxdeを検索してチェック、チェックして出てくる関連のものも全てチェックします。
さらに、lxdmもチェックします。
どうやらこのlxdmがないとログイン画面でどのデスクトップ環境でスタートするか？の選択ができません。

あとはSynapticパッケージマネージャの”適用”を押せば終了です。ログアウトして、
ログイン画面で(多分デフォルトでは)λになっているところを押してlxdeで起動を選択、その後ログインしましょう。

lxterminal のカラーを変えたい！

　 …できません。

Thread: Colour Scheme on lxterminal in lubuntu
と
LXTerminal Colors?
より。

At this time we do not offer any more customization than foreground/background. You are encouraged to run any terminal emulator that meets your needs.

訳すと、”前景色と背景色以上のカスタマイズは提供しないよ。カスタムしたかったら別のターミナルをインストールしてねミ☆”
だそうです。

→guake terminalというのがよさそうです。

sudo apt-get install guake

で、インストールが終わったら端末で

guake

と入力し、F12キーを押せば立ち上がります。guake terminalの設定は
スタートボタン→設定→Guake Preferences
で設定できます。

LXDEのスタートアップ(起動時に自動的に実行させるプログラム)の設定がないよ！

Arch LXDEによると、
ディレクトリの場所：~/.config/lxsession/LXDE/autostart
にLXDEを起動させたときに実行させるプログラムが書いてあります。その中身に何が書いてあるかというと、

@xscreensaver -no-splash
@lxpanel --profile LXDE
@pcmanfm --desktop --profile LXDE
@/usr/lib/policykit-1-gnome/polkit-gnome-authentication-agent-1

のような文が記述されていると思います。意味はArch LXDEによると@以下の文が起動時のプログラムとして実行されます。
なので、ここを書き換えて、たとえばguake端末を起動時に立ち上げたいのならば

@xscreensaver -no-splash
@lxpanel --profile LXDE
@pcmanfm --desktop --profile LXDE
@/usr/lib/policykit-1-gnome/polkit-gnome-authentication-agent-1
@guake

という風に@guakeを付け加えてあげましょう。

guakeの横幅を変えたいよ！

How To Adjust Guake Terminal Width を見てみるとUbuntu12.10以降はguakeの設定ファイルは

/usr/bin/guake

にあります。LinuxMint17.1でも同じで、上のディレクトリにあります。この中身を編集していきます。

sudo emacs /usr/bin/guake

で開き、820~830行目あたりにある

def get_final_window_rect(self):
    """Gets the final size of the main window of guake. The height
    is the window_height property, width is window_width and the
    horizontal alignment is given by window_alignment.
    """
    screen = self.window.get_screen()
    height = self.client.get_int(KEY('/general/window_height'))
    width = 100
    halignment = self.client.get_int(KEY('/general/window_halignment'))

のwidth=100になっているところ書き換えてwidth=50とか80とかにします。
ちなみにこのwidthはウインドウの横幅に対するパーセンテージです。

※サイトで検索した時、下の場所にあるからねーっていう記述がかなりあったけれどこれはUbuntu12.04以前の場合です。
/usr/lib/guake/guake.py
昔のだね。

テキストエディタ, プログラミングと数値計算

フォントサイズ変更

コメントする

emacsでフォントサイズを変更したい場合は？環境はemacs24。

(調べてもよくわからないし出てこない…。)
一度だけ変更したい場合は、Ctrl-x-± で可能です。
ではずっと変更したい場合は？
emacsの設定ファイルに記述します。emacsの設定ファイルの場所は
emacswiki – InitFileより

  1. For GnuEmacs, it is ~/.emacs or _emacs or ~/.emacs.d/init.el.
  2. For XEmacs, it is ~/.xemacs or ~/.xemacs/init.el.
  3. For AquamacsEmacs, it is ~/.emacs or ~/Library/Preferences/Aquamacs Emacs/Preferences.el

にあります。環境によって場所が異なります。
Linuxmint17.1,”sudo apt-get install emacs24″で行った場合、おそらく~/.emacsでしょう。

21.8 Fontsを見るとデフォルトでは
フォント(の種類) : monospace font
フォントサイズ : 10pt
として設定されているそうです。

テキストエディタで~/.emacsを開き、
(custom-set-variables
…
…
)
の括弧の外に

(add-to-list 'default-frame-alist
                       '(font . "DejaVu Sans Mono-12"))

という文を記述します。
現在、フォントのタイプの変更は僕は分かりません。多分DejaVu…を変えればよさそう。
12のところを10とか14とかに変えればデフォルトのフォントサイズを変更することができます。

見出しに使っている画像は8,9,10,11,12,20の場合の比較です。参考にどうぞ。

僕の使ってる~./emacsはこちら

gnuplot

カラーマップの上に線を描く

コメントする

gnuplotでカラーマップの上に2次元で書かれたグラフを書きたいとします。

この場合は

set pm3d map
splot "fort.11" u 1:2:3 with pm3d, "fort.10" u 1:2:($2-$2) with point

とすればokです。
カラーマップの情報はfort.10, 書きたい線のデータはfort.11に書かれているとします。
考えは、2次元のデータをあたかも3次元のデータとして扱うことで解決します。

coloronplot
上のデータを得るためのfortranコードはこんな感じです。

program main
  implicit none
  double precision::x,y,h
 
  h=5.d-2
  y=-3.d0
  do while(y.le.3.d0)
     x=-3.d0
     do while(x.le.3.d0)
        write(11,*)x,y,x+y
        x=x+h
     enddo
     write(11,*)
     
     write(10,*)y,sin(y)
     y=y+h
  enddo

  return
end program main

818 re(1):pm3dによる等高線図（カラーマップ）に2次元グラフを重ねる方法

プログラミングと数値計算

組み合わせ

2件のコメント

組み合わせ\(_nC_r\)、重複組み合わせ\(_nH_r\)の一覧を求めるfortranコードです。

\(_nH_r=~_{n+r-1}C_r\)


組み合わせ\(_nC_r\)の場合

  1  2  3  4
  1  2  3  5
  1  2  3  6
  1  2  4  5
  1  2  4  6
  1  2  5  6
  1  3  4  5
  1  3  4  6
  1  3  5  6
  1  4  5  6
  2  3  4  5
  2  3  4  6
  2  3  5  6
  2  4  5  6
  3  4  5  6

を得たい場合

重複組み合わせ\(_nH_r\)の場合

  1  1  1  1
  1  1  1  2
  1  1  1  3
  1  1  2  2
  1  1  2  3
  1  1  3  3
  1  2  2  2
  1  2  2  3
  1  2  3  3
  1  3  3  3
  2  2  2  2
  2  2  2  3
  2  2  3  3
  2  3  3  3
  3  3  3  3

を得たい場合

組み合わせをrecursionを使わないで得るために、全ての行を初めの値で引いてみました。

+------------+
  0  0  0  0
  0  0  0  1
  0  0  0  2
  0  0  1  1
  0  0  1  2
  0  0  2  2
  0  1  1  1
  0  1  1  2
  0  1  2  2
  0  2  2  2
  1  1  1  1
  1  1  1  2
  1  1  2  2
  1  2  2  2
  2  2  2  2
+------------+

すると、ちょうどr進数と同じになります。なので、これを復元するプログラムを書きました。

プログラミングと数値計算

時間計測

4件のコメント

fortran90において、
このプログラムは何秒かかるか？
早い？遅い？
を調べるためにはもちろん計算時間を計るのが一番です。

  1. 実時間とCPU時間の違い
  2. 実時間計測
  3. CPU時間計測

実時間とCPU時間の違い

『計算時間』には大きく２種類あります。実時間とCPU時間です。

  • 実時間 → 現実の世界での経過時間
  • CPU時間 → プログラムの実行でCPUを使った時間

※[1]より。参考文献とは程遠いですが、僕の認識とあっていて、綺麗な説明と感じたので載せておきます。

例えば、計算時間はそんなにかかってないのに詳細な画像を得たいがために書き出すデータ量を増やしている場合、実時間は長く、CPU時間は短くなります。
また、あるデータ点1つを得るために計算時間は膨大にかかる場合、実時間≈CPU時間になります。

fortranでは時刻を得るためのサブルーチンが既に用意されています。
ここで紹介するのは、実時間を得るための
date_and_time
と
system_clock
の2種類。
CPU時間を得るためのサブルーチンは
cpu_time
の1種類です。

実時間計測(date_and_time)

その場所で何時何分何秒を出力させたい時、その場所に

  write(6,'(3A,i0,A,i0,A,i0,A,i0,A,i0,A,i0,A)')"  == ", &
       c," ",ti(1),"/",ti(2),"/",ti(3), &
       "  ",ti(5),":",ti(6),":",ti(7),", (yyyy/mm/dd  hh:mm:ss)"

を入れましょう[2]。character(10)::b(1:3), integer::ti(1:8)です。

使う際はこうすると良いでしょう。

program main
  implicit none

  call current_time("program start ")  

  !program here
  write(6,*)"press Enter"
  read *
   
  call current_time("program finish")  
 
  stop
end program main

subroutine current_time(c)
  implicit none
  character(*),intent(in)::c
  integer::ti(1:8)
  character(10)::b(1:3)
 
  call date_and_time(b(1),b(2),b(3),ti)
  write(6,*)
  write(6,'(3A,i0,A,i0,A,i0,A,i0,A,i0,A,i0,A)')"  == ", &
       c," ",ti(1),"/",ti(2),"/",ti(3), &
       "  ",ti(5),":",ti(6),":",ti(7),", (yyyy/mm/dd  hh:mm:ss)"
  write(6,*)
 
  return
end subroutine current_time

サブルーチンcurrent_timeを定義して、それを呼び出すだけのほうが分かりやすいかと思います。
引数は何という文言をその場所に指定したいかを示すものです。
実行して適当なときにEnterキーを押してプログラムを進めると、

$ gfortran main2.f90
$ ./a.out
   
  == program start  2016/2/15  9:16:38, (yyyy/mm/dd  hh:mm:ss)

 press Enter

  == program finish 2016/2/15  9:16:40, (yyyy/mm/dd  hh:mm:ss)

$

という結果が得られるでしょう。もちろん、プログラムを動かした時点での時間が表示されます。
一瞬で終わるプログラムの場合は差は見られ無いと思います。

実時間計測(system_clock)

system_clockはfortran標準実装なので汎用性は高いです[4]。system_clockは組み込まれているサブルーチンなので下のプログラムをそのままコピペして使う事が出来ます。

program main
  implicit none
  integer::ti,tf,tr ! ti: initial time, tf: finish time, tr: time rate
  integer::i

  call system_clock(ti)

  !program here
  write(6,*)"press Enter"
  read *

  call system_clock(tf,tr)
 
  write(6,'(f10.3,A)')(tf-ti)/dble(tr),"[s]"
 
  return
end program main

上の文を実行して適当なときにEnterキーを押してプログラムを進めると、

$ gfortran main2.f90
$ ./a.out
    press Enter
      1.283[s]
$

という出力が得られます。

CPU時間の計測(cpu_time)

CPU時間の計測するには

    call cpu_time(t0)
    ...
    call cpu_time(t1)
    write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"

を入れましょう[3]。real::t1,t2です。

program main
  implicit none
  real::t0,t1
  integer::i

  call cpu_time(t0)

  !program here
  write(6,*)"press Enter"
  read *
 
  call cpu_time(t1)
 
  write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"
 
  stop
end program main

でokです。適当な時間待って、Enterキーを押すと

$ gfortran main2.f90
$ ./a.out
    press Enter
     0.000[s]

という出力が得られるでしょう。
これはcpuを動かしていないためであり、cpuが動いていた時間というのは限りなく0だ、ということです。

参考文献

[1]ユーザ時間とシステム時間の違いを教えてください。
[2]1.4.7.1 date_and_time: 日付と時刻の取得 -ORACLE®
[3]8 移植性のある時間計測の方法 -nag
[4]9.254 SYSTEM_CLOCK — Time function

プログラミングと数値計算

大きな数を扱う

2件のコメント

大きい数＝工夫or対数!

大きい数を扱う…例えば階乗を計算しろ、という問題や組み合わせ\(_nC_r\)を計算しろ、という問題に時々あたります。

まず、典型的な例として組み合わせ
\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)
を計算しましょう。
この計算はそのまま定義のまま計算しようとすると階乗が出てくるので、途中の値は物凄くでかい数字になるのですが、最後の答えは小さい値になるはずです。それなのに計算できないのはおかしくない!?工夫次第で何とかなるものです。
下の表は３つの計算方法についてまとめたものです。

integer(4バイト整数型±2 147 483 647)を用いた計算
定義のまま計算 工夫して計算 対数を利用して計算
最大のn,r \(_{12}C_6\) \(_{29}C_{14}\) \(_{33}C_{16}\)
理由 階乗の計算によるオーバーフロー “割り切れる”ための制約 (限界値)

integer(8バイト整数型±9 223 372 036 854 775 807)を用いた計算
計算方法 定義のまま計算 工夫して計算 対数を利用して計算
最大のn,r \(_{20}C_{10}\) \(_{61}C_{30}\) \(_{48}C_{24}\)
理由 階乗の計算によるオーバーフロー “割り切れる”ための制約 倍精度型変数の有効桁数が足りない
定義のまま計算

例えばfortranでintegerの宣言により定義した場合、階乗が正しく計算できる範囲(オーバーフローしない範囲)は、\(12!=479\ 001\ 600\)
まで計算できます。
変数の型がいくつまで計算できるかは、組み込み関数hugeを使うことで確認できます。

program main
  implicit none
  integer::n

  write(6,*)"huge",huge(n)

  stop
end program main

これで確認すると、整数型は
\(\pm 2\ 147\ 483\ 647\)
までの値なら代入することができるため、
\(13!=6\ 227\ 020\ 800\)は計算できないことがわかります。
一応関数はこんな感じ。

function nCr_fact(n,r)
  !sikinote
  implicit none
  integer::nCr_fact,fact,n,r
  external::fact
 
  nCr_fact=fact(n)/(fact(n-r)*fact(r))
 
  return
end function nCr_fact
function fact(n)
  implicit none
  integer::fact,i,n
 
  if(n.le.-1)write(6,*)"####warning#### parameter of factorial has negative value"
  fact=1
  do i=2,n
     fact=fact*i
  enddo

  return
end function fact

( ※余談ですが、8バイト型整数で宣言、すなわちinteger(8)で宣言すると
\(9\ 223\ 372\ 036\ 854\ 775\ 807\)
まで計算できます(19桁、\(20!=2\ 432\ 902\ 008\ 176\ 640\ 000\)まで)。)

なので定義通りの計算はn=12までが限界です。実用的じゃありません。

工夫して計算

\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)を工夫します。

\(
\begin{align}
\displaystyle _nC_r&=\frac{n!}{(n-r)!r!} \\
&=\frac{n(n-1)(n-2)\cdots(n-r+2)(n-r+1)}{r(r-1)(r-2)\cdots2\cdot 1} \\
&=\frac{n}{r}\cdot \frac{n-1}{r-1}\cdot \frac{n-2}{r-2}\cdots \frac{n-r+2}{2}\cdot \frac{n-r+1}{1} \\
&=\prod_{i=1}^r\frac{n-r+i}{i}
\end{align}
\)
として計算します。こうすれば階乗みたいに大きな数を計算する必要がなくなります。
関数を書けばこうなります。

function nCr(n,r)
  !sikinote
  implicit none
  integer::n,r,i,r0,nCr

  r0=n-r
  if(r.le.r0)r0=r

  nCr=1
  do i=1,r0
     nCr=nCr*(n-r0+i)
     nCr=nCr/i
  enddo
 
  return
end function nCr

で\(_nC_r\)を求めることができます。
上のプログラムでは、最大\(_{29}C_{14}=77\ 558\ 760\)まで求めることができます。
これは絶対に割り切れることを前提にしているためにおこるもので、

nCr=nCr*(n-r0+i)

の文のところで最大値が決まってしまうためです。
定式化すれば、
式\(_nC_r\)に対し、\(_{n-1}C_{r-1}\cdot n\)が扱える整数値を超えないこと
と表現できます。

\(_{29}C_{14}=77\ 558\ 760\)が計算できるのは、
\(_{29-1}C_{14-1}*29=1\ 085\ 822\ 640\)
であるので計算可能です。次の\(_{30}C_{15}\)を計算するためには
\(_{30-1}C_{15-1}*30=2\ 326\ 762\ 800\)が
integerの最大の整数値\(\pm 2\ 147\ 483\ 647\)
を超えてしまうのでこれ以上計算はできません。
※もしもinteger(8)を用いると\(_{61}C_{30}\)まで計算できます。

対数を利用して計算

もう一つ対数を利用した方法を紹介します。
対数を利用すると、
\(\displaystyle _nC_r=\frac{n!}{(n-r)!r!}\)は、\(S= _nC_r\)とおくと
\(
\begin{align}
\displaystyle \ln(S)&=\ln\left[\frac{n!}{(n-r)!r!}\right] \\
&=\ln(n!)-\ln\{(n-r)!\}-\ln(r!) \\
&=\sum_{i=n-r+1}^n\ln(i)-\sum_{i=2}^{r}\ln(i)
\end{align}
\)
と書けます。よって、
\(\displaystyle S=\exp\left[\sum_{i=n-r+1}^n\ln(i)-\sum_{i=2}^{r}\ln(i)\right]\)
です。プログラムを書けば

function nCr_log(n,r)
  !sikinote
  implicit none
  integer::n,r,i,r0,nCr2
  double precision::tmp
 
  r0=n-r
  if(r.le.r0)r0=r

  tmp=0.d0
  do i=n-r0+1,n
     tmp=tmp+log(dble(i))
  enddo
  do i=2,r0
     tmp=tmp-log(dble(i))
  enddo

  nCr2=nint(exp(tmp))  

  return
end function nCr_log

となります。この場合は\(_{n}C_{r}\)が整数型で扱える範囲を越えなければいいという条件だけになるので、
integerでは\(_{33}C_{16}\)までokです。

integer(8)では\(_{66}C_{33}\)までできます…が、上のプログラムそのままではできません。
おそらく、組み込み関数nint(実数型を整数型に四捨五入して代入する)がinteger(8)に対応していない(かも)ということと、倍精度の有効桁数がだんだんと足らなくなっていくので厳しいです。後者による問題によって、確認した範囲では\(_{48}C_{24}\)位が限界です。

プログラミングと数値計算

乱数

コメントする

fortran90においての乱数の発生方法です。

乱数を１から作るのは、乱数を研究するとかでない限り止めましょう。
ここではfortran90で乱数を発生させるためにどうすればいいか？を記述します。

私は乱数について詳しくありませんが、調べた限りメルセンヌツイスタという乱数発生法が良い乱数を発生するようです。
メルセンヌツイスタの詳細はMersenne Twister Home Page にあるのでご参照ください。
fortran90コードはhttps://gist.github.com/ykonishi/5569005にあります。

上記のリンクから、メルセンヌツイスタのfortran90コード（mt19937.f90）をダウンロードします。
そして、メインプログラム

program main
  use mt19937
  implicit none
  integer::i
  double precision::d

  call sgrnd(2) ! seed
 
  do i=1,10
     write(6,*)grnd()
  enddo
 
  stop
end program main

をmt19937.f90と一緒に

gfortran -fno-range-check mt19937.f90 main2.f90

というオプションを付けてコンパイル（※1）します。実行すると、

$ ./a.out
   6.4690865343436599E-002
  0.40996560384519398    
  0.14283204451203346    
  0.74749888177029788    
  0.59957117028534412    
  0.53676494420506060    
  0.38914293772540987    
  0.94303490873426199    
  0.15882158395834267    
  0.15933134709484875    
$

という結果を得ることが出来ます。

（※1）
このオプションが、型が扱える範囲を超えていても無視するためのオプションです。
何故かgfortranコンパイラ(ver4.8.4で確認)で出ます。
そして、これはコンパイラの問題だと私は結論付けました。
fortranの整数は
-2147483648から2147483647までで定義されているのにもかかわらず、
gfortran(ver4.8.4)は
-2147483647から2147483647の範囲でなければエラーを出すようです。
しかし、実際に整数に-2147483648を代入し、このエラーを無視する上のオプションを付けて実行すると、ちゃんと値が入ります。なので、コンパイラに問題があると判断しました。

[adsense1]

任意の関数に従う乱数(von Neumannの棄却法)

このページのサムネイル画像の右は等方的２次元調和振動子励起状態の密度
\(
\begin{align}
f(x,y)=\frac{4}{\pi}x^2y^2e^{-(x^2+y^2)}
\end{align}
\)
を点の濃さで表現するためのプログラムです。

これは、上の関数に従う乱数分布を書くことにほかなりません。
一様乱数を任意の関数に従う乱数に変換する方法として、
von Neumannの棄却法と呼ばれる方法があります。

以下のようにすると一様乱数を関数\(f(x)\)に従う乱数に変えることが出来ます。

\(x\)の範囲\([x_a,x_b]\)で定義された関数\(f(x)\)に従う乱数を発生させたい。
区間\([x_a,x_b]\)で関数は\([f_a,f_b]\)の値を持つとすると、
　1.　範囲\([x_a,x_b]\)の一様乱数\(x_r\)を生成する。
　2.　範囲\([f_a,f_b]\)の一様乱数\(f_r\)を生成する。
　3.　もしも\(f_r\le f(x_r)\)ならば、その\(x_r\)は\(f(x)\)に従う乱数である。そうでなければ、発生させた乱数は捨てる。
　4.　1-3を繰り返す。
という方法です。アルゴリズムを見て分かる通り、この方法は無駄が多いです。
発生させた乱数を捨てる操作は出来ればしたくありません。
ですが、この方法は非常に簡単に実装できるのでとりあえず実装したいという場合には良い方法です。

以下は、上の考えの二次元版です。

program main
  use mt19937
  implicit none
  integer::i,count,N
  double precision::xp,yp,fp
  double precision::a,b,fmin,fmax
  double precision,external::f
 
  call sgrnd(2)

  N=2000
 
  ! fmin :: minimum value of function f(x,...)
  ! fmax :: maxmum value of function f(x,...)
  fmin=0.d0
  fmax=1.d0

  ! range of random number [a,b]
  a=-5d0
  b= 5d0
 
  open(13,file="./density.d")
  count=0
  do while(count.lt.N)
     xp=grnd()*(b-a)+a
     yp=grnd()*(b-a)+a
     fp=grnd()*(fmax-fmin)+fmin
     
     if(fp.le.f(xp,yp))then
        write(13,*)xp,yp
        count=count+1
     endif
  enddo
  close(13)

  stop
end program main

function f(x,y)
  implicit none
  double precision::f
  double precision,intent(in)::x,y

  double precision::pi=acos(-1.d0)
 
  f=abs(sqrt((1.d0/pi))*2d0*x*y*exp(-0.5d0*(x*x+y*y)))**2
 
  return
end function f

カラーマップと３次元での表現はこうなります。
20150524-210920_1_c

乱数を用いた密度表示(下のプログラム)ではこう表現されます。
nxny11density_c

[adsense2]

参考

任意分布の乱数生成　https://www.slideshare.net/shogoosawa581/ss-65259938

以降はfortranの標準組み込み関数を用いる場合のものです。
消すのは忍びないため、一応おいておきます。

サバイバルゲーム, 弾道計算, 物理学

弾道計算(BB弾)の理論

14件のコメント

エアガンから発射したBB弾がどのように飛んでいくか?
BB弾の弾道計算理論パートです。

完全な計算のためには圧縮ナビエ・ストークス方程式を解いて…ということをしなければなりませんが、そこまでは考えません。
射出後のBB弾がどのような軌道を描き進むのか、ニュートンの運動方程式の範囲で考えていき,定量的な一致を目標にしていきます。

結果として得られる運動方程式は以下の２つです。
・BB弾の運動方程式
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|\vec{V}
-C_l \frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
・BB弾の回転角速度の減衰を記述する方程式
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)
の二つにより構成されます。

実験データから、\(C_l=0.12\)で良く記述できることが分かりました。
詳細はBB弾の回転量について(実験との比較)をご覧ください。

結論を言うと、サバゲーで勝ちたければ、重いBB弾を使うべきです。
飛距離を伸ばすためには
BB弾の重さ、銃口から出てくるときの初速と回転数以外に飛距離を伸ばすことに関係する変数はありません。
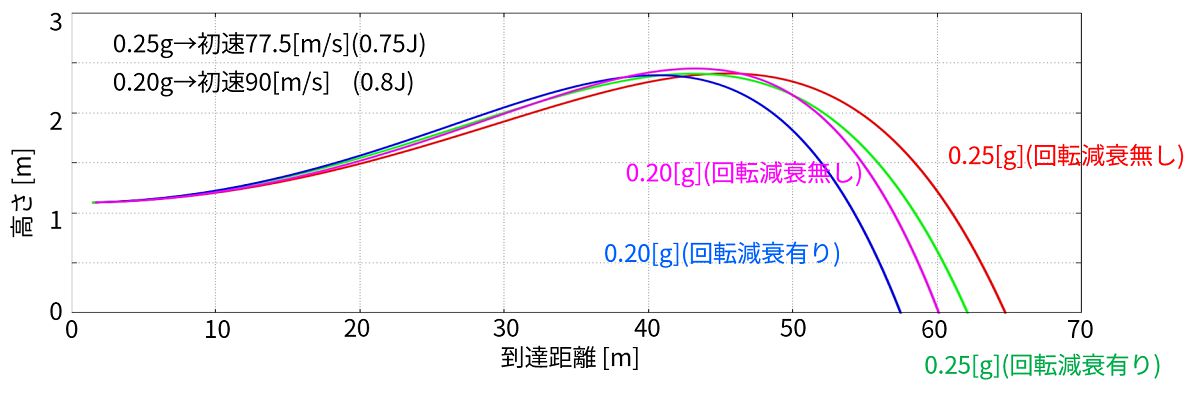
0.20,0.25gの違いと回転減衰
※初速と共に載せました。この初速の値は実験データがあるサイトと同じ値にしています。

追記）2019年6月20日
空気抵抗を1%程多めに見積もっていました。結果はそんなに変わらないと思いますが、記述しておきます。式は訂正しましたが、グラフは訂正していない時の計算式に従っています。時間がある時に修正いたしますので、ご了承下さい。

追記）2021年8月11日
グラフなどを修正しました。

目次

  1. 先行研究の紹介
  2. BB弾に働く力
  3. BB弾の運動方程式
  4. 結果
  5. 流体中に置かれた球体の回転の減衰
  6. 参考文献

弾道計算に関するその他ページ
弾道計算(BB弾)の理論←今ここ
BB弾の回転量について(実験との比較)
弾道計算(BB弾)の結果
弾道計算の結果2, 比較と詳細データ
弾道計算(BB弾)のコード(fortran90)
弾道計算のコード(Excel)
バレル内部でのBB弾の方程式
水中下でのBB弾の弾道計算

先行研究の紹介

誰かやっているかなーっと調べてみると、やっぱりやってる人がいました。

解析解(慣性抵抗とマグヌス力を考慮?)を用いての、定性的な一致に終わっています。
BB弾の弾道計算まとめ -チン太さんのノート(2013年)
(※2016/01/16 正しさの確認がとれないので一応の解析解、ということにしておきます。なぜなら、2次元の空気抵抗を考慮した微分方程式でさえ解析解が存在しないはずだからです[12]。)

本稿では可能な限りの影響を考慮し、定量的に一致させることを目標にしていきます。

BB弾に働く力

質量mのBB弾の場合、運動方程式は言葉で書けば、
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=(\mbox{重力})+(\mbox{風の抵抗力})+(\mbox{回転による揚力})
\)
で十分だと思います。

また、角速度ベクトルの歳差運動はあるかもしれませんが、見積もる方法が分からなかったため考慮していません。

追記)
各々の力の大きさを簡単に計算してみました。BB弾の速さを100m/s, 重さ0.2g, 166回転/sと仮定

重力: \(1.96\times 10^{-3}\)

慣性抵抗力: \(8.52\times 10^{-2}\)
Magnus力: \(1.71\times 10^{-3}\)
コリオリ力(最大): \(2m|\vec{\omega_{earth}}||\vec{v}|=2.8\times 10^{-6}\)

であるため、コリオリ力はほとんど無視できるんじゃないでしょうか。

重力\(F_g\)

場所による重力加速度の違いはあるかもしれませんが、無視できるでしょう。
なので重力\(F_g\)の大きさは
\(F_g=mg\)
でしょう。ここで

  • \(m\ \mathrm{[kg]}\) : 物体の質量
  • \(g\ \mathrm{[m\cdot s^{-2}]}\) : 重力加速度

です。

風の抵抗力\(F_d\)

空気抵抗と呼ばれているものです。
空気抵抗を計算するには物体の形状が分からなければ求めることはできません。
速度に比例する項は理論的に求めることができますが、速度の2乗に比例する空気抵抗の係数(抗力係数)はレイノルズ数の関数となります。

ここでは、半径\(R\)の完全な球体に働く空気抵抗を求め、それを導出、計算します。

風(流体)の抵抗力の大きさ\(F_d\)は一般には次元解析により
\(
\displaystyle F_d=\frac{\eta^2}{\rho}\sum_{n=1}^{\infty}K_n \left(\frac{v \rho L}{\eta}\right)^n
\)
として与えられます[1]。ここで

  • \(\eta\ \mathrm{[kg \cdot m^{-1}\cdot s^{-1}]}\) : 流体の粘性率(Viscosity) ※動粘度ではないです。
  • \(\rho\ \mathrm{[kg \cdot m^{-3}]}\) : 流体の密度
  • \(v\ \mathrm{[m\cdot s^{-1}]}\) : 物体の速度の大きさ
  • \(L\ \mathrm{[m]}\) : 物体の大きさ(半径\(R\)の球の場合、\(L\)は直径\(L=2R\)に相当する量)
  • \(\frac{v \rho L}{\eta}\) : レイノルズ数(\(R_e\),Reynolds number)と呼ばれる無次元量

です。次元解析から具体的な定数の値\(K_n\)を求めることはできません。
通常の場合はn=1(粘性抵抗)とn=2(慣性抵抗)のみ考慮されます。
速度の3乗以上に比例する項というのは見かけません。
おそらく、これから説明する抗力係数\(C_d\)にその効果を全部押し込めているためでしょう。

上の式を速度の関数\(C_d\)を用いて
\(F_d=C_d S \left(\frac{1}{2}\rho v^2\right)\)
と書きます。ここでSは速度に垂直な、物体の断面積です。
今、\(n=2\)以外の項を全て\(C_d\)の中に入れました。

\(C_d\)は抗力係数(Drag Coefficient)と呼ばれ、
これはレイノルズ数の関数となり、
\(C_d=C_d(R_e)\)
となります。
この抗力係数は非常に厄介らしいです。物体の形状に依存したりするらしく、球の場合でも、どうやら実験的に求められているようです。
Wikipediaの抗力係数のページに若干の記述があります。
球の場合の抗力係数の関数\(C_d(R_e)\)をフィッティングした関数は論文[2]より、
\(
\displaystyle C_d=\frac{24}{R_e}+\frac{2.6\left(\frac{R_e}{5.0}\right)}{1+\left(\frac{R_e}{5.0}\right)^{1.52}}
+ \frac{0.411\left(\frac{R_e}{263000}\right)^{-7.94}}{1+\left(\frac{R_e}{263000}\right)^{-8.00}} + \left(\frac{R_e^{0.80}}{461000}\right)
\)
として書けるそうです。実際にプロットしてみるとこんな感じです。
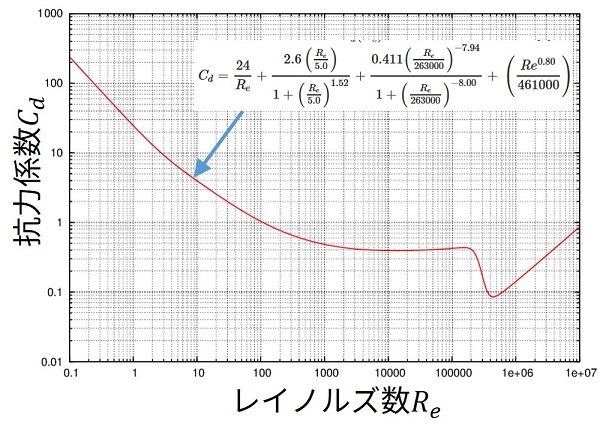
Cdグラフ
確かに抗力係数のグラフと同じようになります。

よって半径Rの球の場合、風の抵抗力\(F_d\)の大きさは結局、
\(
\begin{align}
F_d &= C_d S \left(\frac{1}{2}\rho v^2\right) \\
&= \frac{1}{2} C_d \rho \pi R^2 v^2
\end{align}
\)
として与えられます。

※BB弾をエアガンから、無風状態で発射する場合、抵抗は


風の抵抗力: \(8.52\times 10^{-6}|\vec{v}|^2\)

となります。ここでいう風の抵抗力は、粘性抵抗と慣性抵抗を含んだものです。

回転による揚力\(F_L\)

回転による揚力の発生はマグヌス効果(Magnus effect)と呼ばれています。
空気力学で、回転する円柱の揚力に関する理論クッタ・ジュコーフスキーの定理(Kutta–Joukowski theorem)によって回転による揚力は記述されます。
発生する揚力\(F_L\)の大きさは
\(
F_L=\rho \Gamma v
\)
と書けます[3]。ここで

  • \(\rho\ \mathrm{[kg \cdot m^{-3}]}\) : 流体の密度
  • \(v\ \mathrm{[m\cdot s^{-1}]}\) : 物体の速度の大きさ
  • \(\Gamma\ \mathrm{[m^2\cdot s^{-1}]}\) : 循環

を意味します。循環\(\Gamma\)は
\(
\displaystyle \Gamma=\oint_s \vec{v}\cdot d\vec{s}
\)
という量です。
ここで、\(\oint\)は球体の外側での閉経路に対する線積分であり、球体そのものの循環ではありません[9]。

私は流体力学は良く知らないで余り突っ込まないでおきますが、簡単に仮定します。
実際に発生する循環\(\Gamma\)を無次元の係数\(C_l\)と球体の循環\(\Gamma^{sp}\)を用いて、
\(
\Gamma=C_l\Gamma^{sp}
\)
で書ける、とします。
（実際には迎え角なども関係するようなのでこれは厳密には正しくはありませんが、定性的に説明するので良いでしょう、という仮定しているだけにすぎません。）

球の循環を考えます。
半径\(R\mathrm{[m]}\)の角速度\(\omega\mathrm{[s^{-1}]}\)を持つ円盤に対して循環\(\Gamma^{ci}\)を計算すると、
\(
\begin{align}
\Gamma^{ci} &= \oint_s \vec{v}\cdot d\vec{s} \\
&= \int_0^{2\pi}R\omega\cdot Rd\theta \\
&= 2\pi R^2 \omega
\end{align}
\)
と計算できます。しかし、これから考えるのは球です。
半径\(r\)の円盤に対して循環は、\(\Gamma^{ci}=\Gamma^{ci}(r)=2\pi r^2 \omega\)と書くことができるので、積分して球の循環\(\Gamma^{sp}\)が求められます。
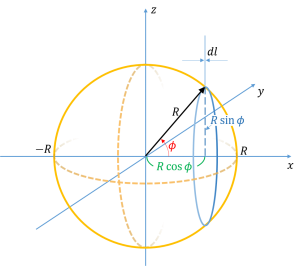
球に対する循環の計算
図のように考えれば、計算は、
\(
\begin{align}
\Gamma^{sp} &= \int_{-R}^{R} \Gamma(r) dl \\
\end{align}
\)
です。\(l=R\cos\phi, \ \ r=R\sin{\phi}\)の変数変換を行って計算すると、
\(
\begin{align}
\Gamma^{sp} &= \int_{-R}^{R} \Gamma(r) dl \\
&= 2\pi \omega R^3 \int_0^\pi \sin^3\phi d\phi \\
&= \frac{4}{3}\pi R^3 \cdot 2\omega
\end{align}
\)
と求められるため、揚力\(F_L\)は無次元の係数\(C_l\)を用いて
\(
\begin{align}
F_L &= C_l \rho \Gamma^{sp} v \\
&= C_l \frac{4}{3}\pi R^3 2\omega \rho v
\end{align}
\)
と書き表せるとします。

2016/07/09 追)
係数\(C_l\)は実験[11]とその弾道データより、
\(
C_l=0.12
\)
で良く近似される、という事が分かりました。詳しくは
BB弾の回転量について(実験との比較)
をご覧ください。

BB弾の運動方程式

重力\(F_g\), 空気抵抗\(F_d\)と回転による揚力\(F_L\)を取り入れたBB弾に対する運動方程式は方向も考慮に入れて、
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}
-\frac{1}{2}C_d \rho \pi R^2 |\vec{v}|\vec{v}
-C_l\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{v}|\frac{\vec{v}\times\vec{\omega}}{|\vec{v}\times\vec{\omega}|}
\)
と書けます。上の式の場合、風速の影響は入っていません。
風速の影響を取り入れるのは風と共に動く座標系で考えてから元の座標系に戻ればいいです。
すなわち、地表に固定した座標に対して風の速度ベクトル(定ベクトル)を\(\vec{u}\), 物体の速度ベクトルを\(\vec{v}(=d\vec{r}/dt)\), とし、
相対的な速度ベクトルを\(\vec{V}=\vec{v}-\vec{u}\)と定義すると、風がある中での運動方程式は、
\(
\displaystyle m\frac{d^2 \vec{r}}{dt^2}=
-mg\vec{k}+-\frac{1}{2}C_d \rho \pi R^2 |\vec{V}|\vec{V}
-C_l\frac{4}{3}\pi R^3 2\rho |\vec{\omega}| |\vec{V}|\frac{\vec{V}\times\vec{\omega}}{|\vec{V}\times\vec{\omega}|}
\)
と書けます。

それぞれの定数の具体的な値を考えます。

各定数の値
名称 記号 捕捉
重力加速度\(g\) \(9.80665\mathrm{[m\cdot s^{-2}]}\)
空気の粘性率(Viscosity)\(\eta\) \(18.2\times 10^{-6}\mathrm{[kg \cdot m^{-1}\cdot s^{-1}]}\) 空気中20度において。また、粘性率は数十気圧から数気圧の間圧力には依存しません。
が、温度に依存し、ある温度\(T_1[K]\)での粘性率\(\eta_1\)が分かっているならば、
温度\(T_2[K]\)での粘性率\(\eta_2\)はサザランドの定数Cを用いて、
\(
\eta_2=\eta_1 \left(\frac{T_1[K]+C}{T_2[K]+C}\right)\left(\frac{T_2[K]}{T_1[K]}\right)^{3/2}
\)
と記述されます。空気の場合、C=117です[4]。
乾燥した空気の密度\(\rho\) \(1.205\mathrm{[kg \cdot m^{-3}]}\) 乾燥した空気の密度は温度と圧力に依存します。温度\(t[℃]\)、圧力をH[torr]とすると
\(
\rho=\frac{1.293}{1+0.00367t[℃]}\cdot \frac{H[torr]}{760}
\)
です[5]。
BB弾の半径\(R\) \(3.0\times 10^{-3}\mathrm{[m]}\)

数値計算は刻み幅制御ルンゲ・クッタ法を用います。
コードはこちら→弾道計算(BB弾)のコード

[adsense1]

結果

結果をまとめます。

回転数と飛距離依存性

撃ちだしの角度を地面と水平にして、同じエネルギー(0.90J)で撃ち出した場合の回転数による飛距離の変化を見てみましょう。

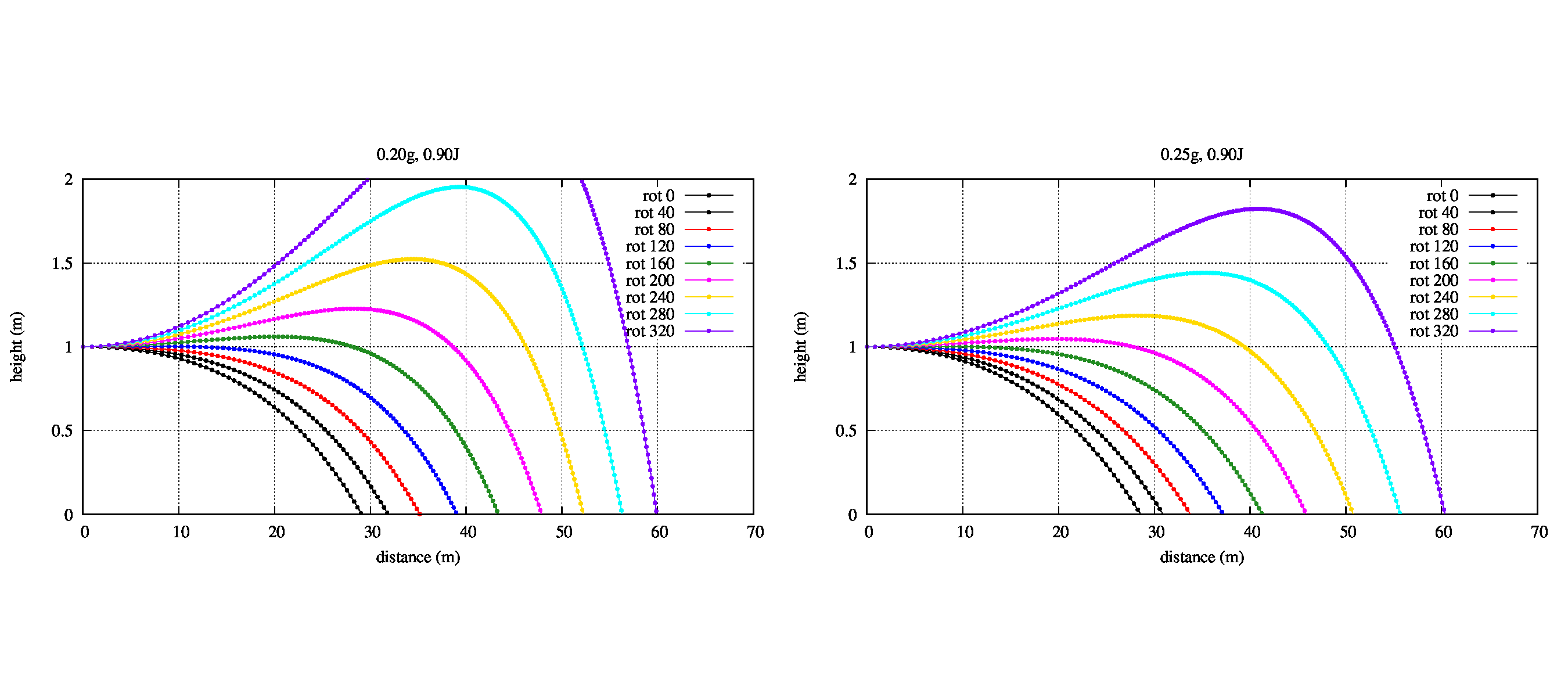
図の横軸は進行方向の距離、縦軸は高さを表し、グラフの色『rot XXX』は、XXX回転/秒を表します。
重たい0.25gの方が、回転数が変化しても軌道が変わりにくいことが分かります。
つまり、0.25gの方がいつも安定して飛ばせる、一発ごとにぶれが少ないということが分かります。

理想的な弾道の軌跡

BB弾の回転数が程よく遠くに飛ぶのは、0.20gで240回転/秒、0.25gで280回転/秒くらいがよさそうな軌道と考えます。
この時、打つ際に若干、下方向に向けて打つことでまっすぐ飛ぶ領域を増やせそうです。どのくらい下向きに打てばいいんでしょうか。その結果がこれです。

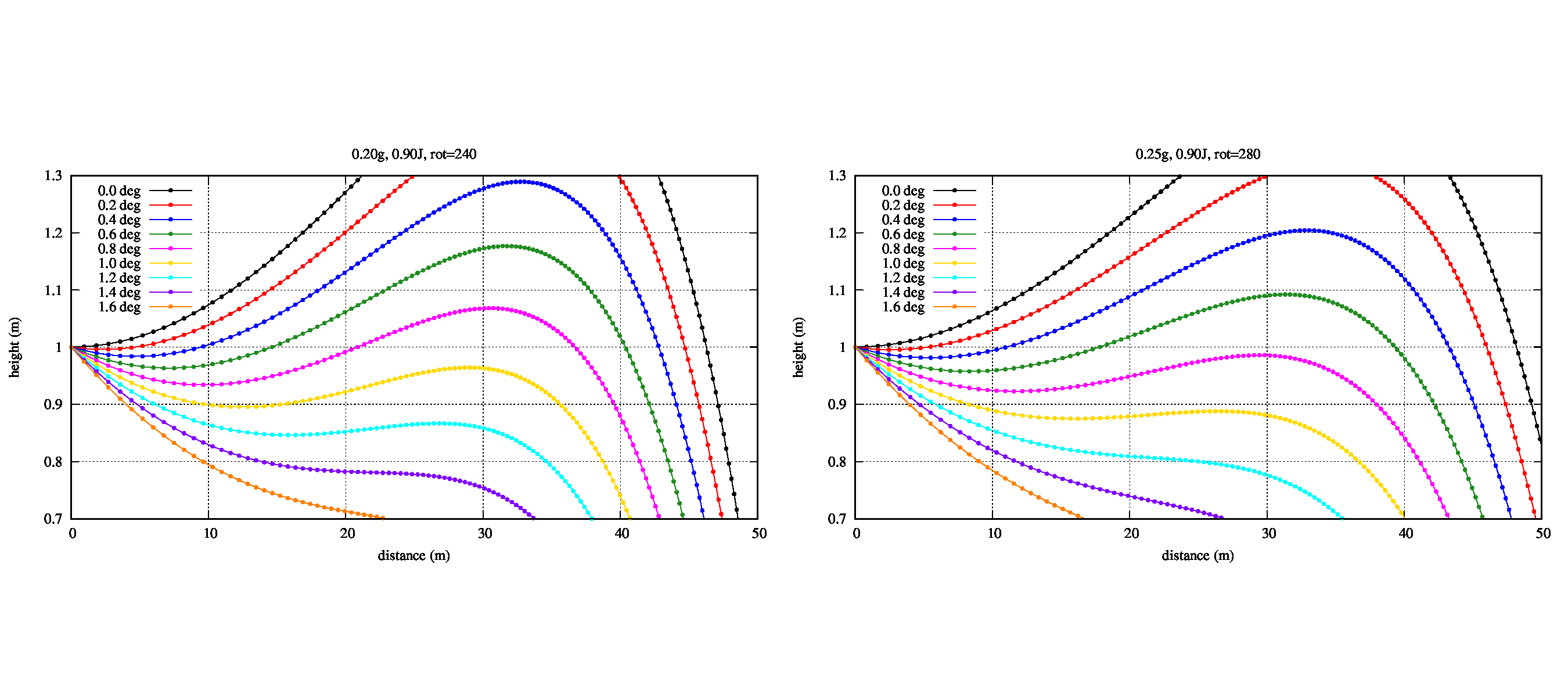
図の横軸は進行方向の距離、縦軸は高さを表し、グラフの色『XXX deg』は、進行方向下向きに角度XXX度で射出したことを表します。

この結果から、一つの最適な軌道を与えるのは0.20gで回転数240回転/秒かつ角度0.8°,0.25gで回転数280回転/秒かつ角度0.6° で射出した時でしょう。その時の上下方向のブレは35m位飛んで10cmくらいであることが分かります。

また、一つ言えるのは一番良い軌道は角度\(\theta\)を変化させたときに上下方向のブレが少ないとき、と言えると思います。
なのでこの値が厳密な最適ではないです。ですが、今まで、最適ホップと言われるような曖昧な定義ではなく、最適な良い軌道の定義について指針ができそうです。

BB弾の重さ0.20gと0.25gの違い

さて、BB弾の重さによって弾道が変わる様子を調べてみましょう。余計な要因をなくすために、回転なし、風なし、同じエネルギー（0.90J）で射出した場合で比較しましょう。

まずは着弾する際の速度についてです。

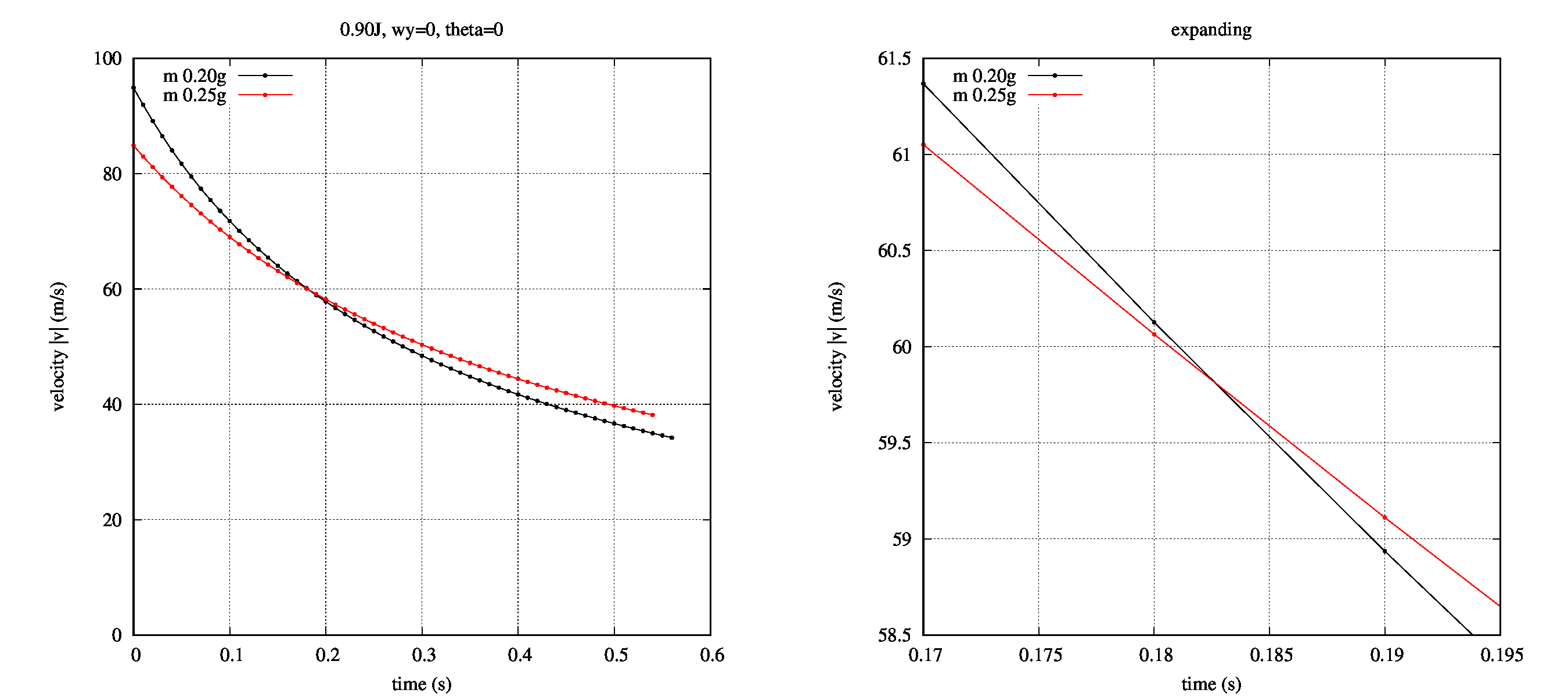
左図中の横軸は時間、縦軸は球の速さを表し、黒(赤)色は0.20g(0.25g)の場合です。
右図は左図と同じですが、軸の範囲を変更して交差する付近を拡大しています。

0.25gの方が着弾までの速度変化が少ないことが分かります。
つまり、空気の影響を受けにくいことを示します。これは、球が重いほうが風の抵抗力があたかも小さくなるからです。

続いて、着弾までの時間についてです

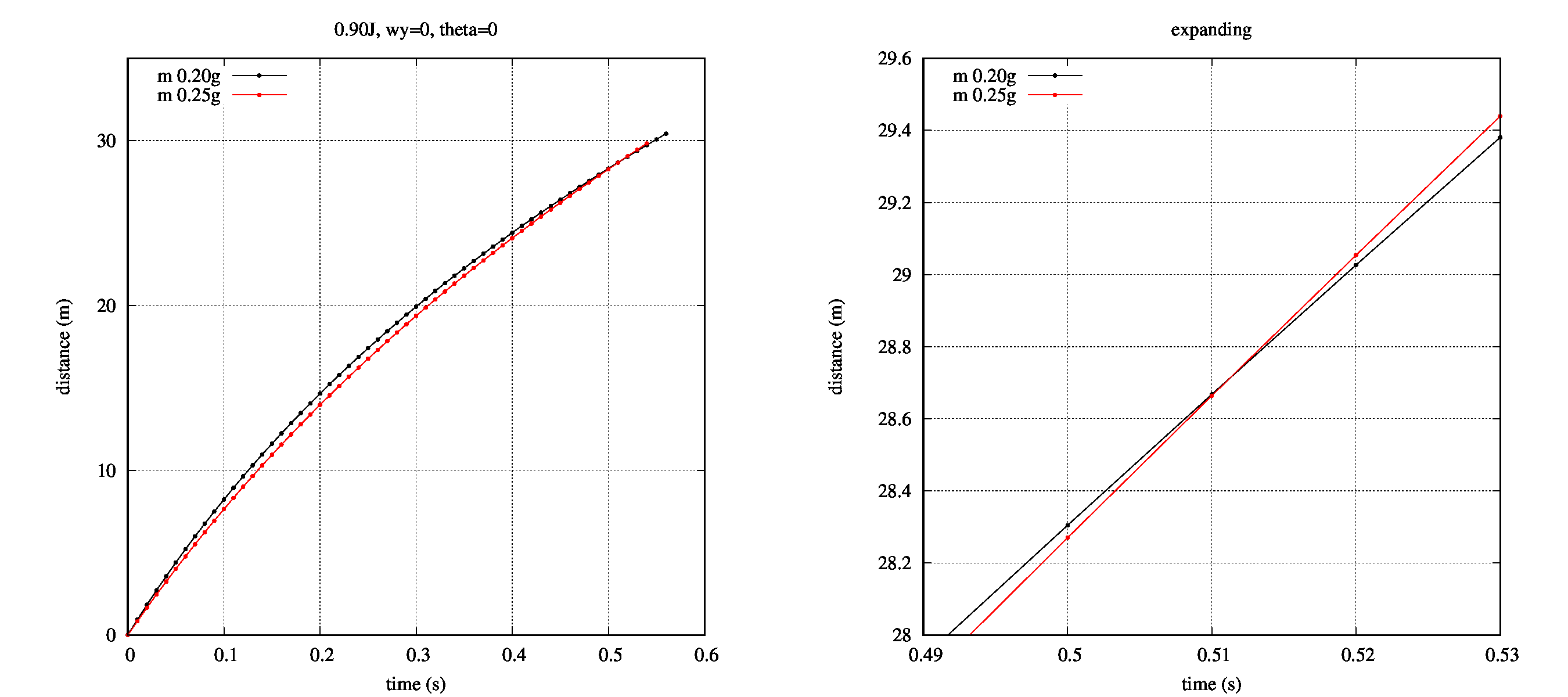
左図中の横軸は時間、縦軸は球の進行方向の距離を表し、黒(赤)色は0.20g(0.25g)の場合です。
右図は左図と同じですが、軸の範囲を変更して交差する付近を拡大しています。

着弾までに早いということは、着弾までのずれがなく、撃った時と着弾までのラグがないということです。
具体的に、到達するまでの時間を見ると30[m]まで0.20gのBB弾のほうが早く到達するようですね。
ですが、その差は0.01秒程度ですので、そんなに実感はできないかと思います。

重さと風の影響

良い軌道と決めたパラメータ（0.20gで240回転/秒, 0.25gは280回転/秒として計算をしています。エネルギーは0.9Jのエネルギーを持つようにしています。

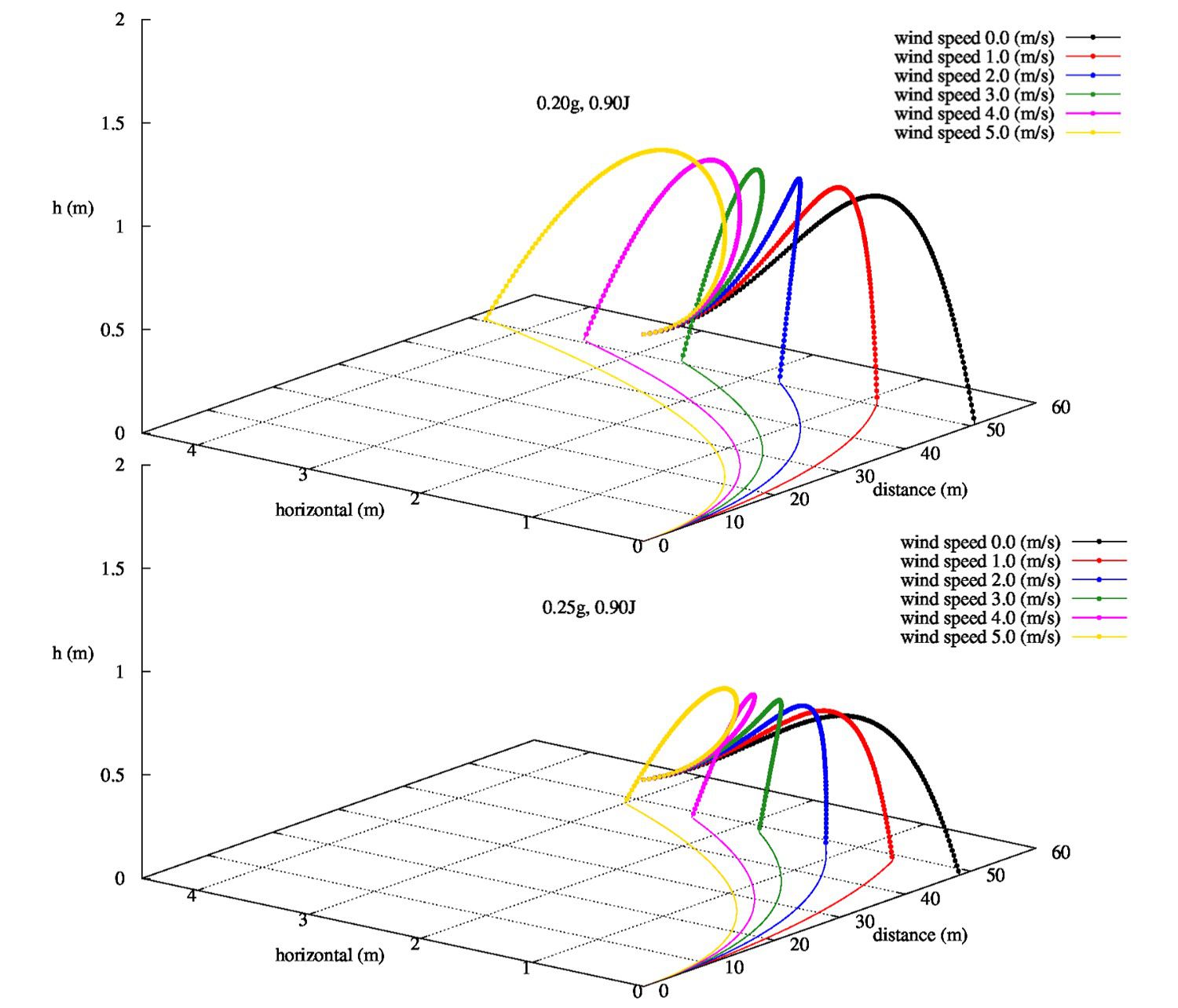
0.2gと0.25gの違いと風の影響は余りなさそうな気がします。例えば30[m]地点ではどちらも5[m/s]の風が吹いていたとしても1.0~1.3[m]のずれに収まっています。
この30cmが問題になるのかは…状況次第ですね。

横向きに打ち出した時の曲がり具合

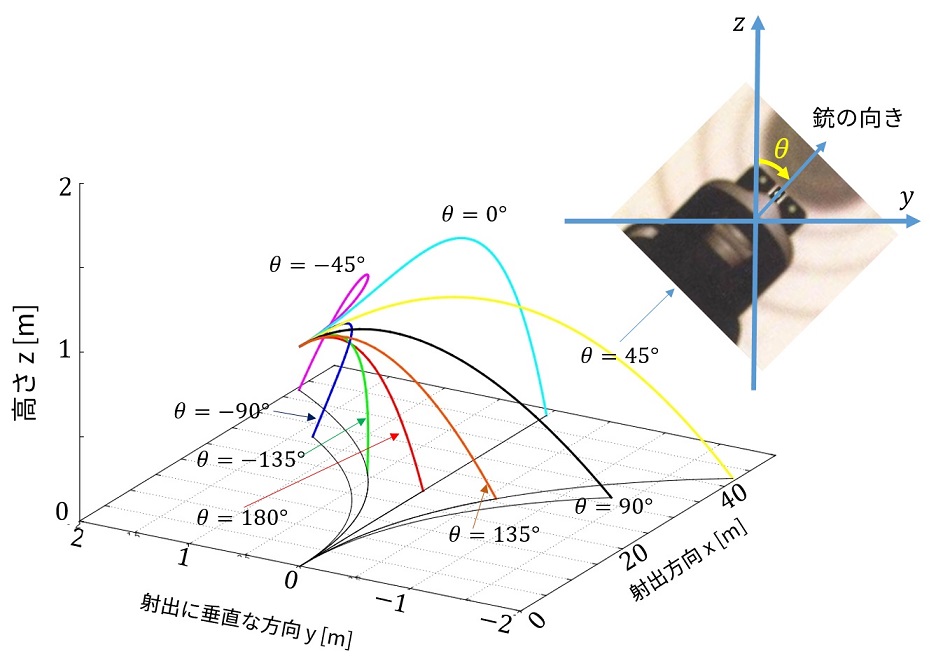
横向き射出2
意外と曲がらないものですね。大体2[m]です。
理由は、この計算では打ち出す時は銃を完全にまっすぐにして固定した状態なのでMagnus力の影響が0から段々と強くなります。
Magnus力の強さは回転軸に垂直の速度成分が速いほど加速度的に増えていくものなので、はじめ銃を曲がる方向に向けて撃てば
曲がる方向の初速度+更なるMagnus力でもっと曲がります。
なので物陰にいる敵を倒す(褒められた方法ではないですが)場合は若干敵の方向へ向けて回転による効果を得られるようにしましょう。

銃を逆さまにして上から狙う

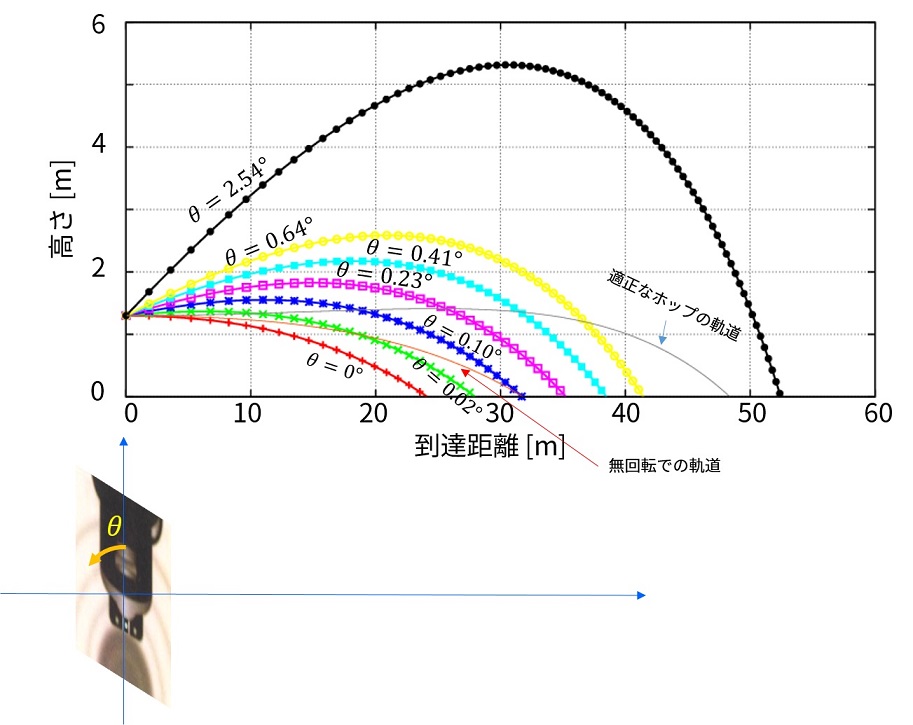
上から落として狙う
じゃあ銃を逆さまにして上向きに撃てば障害物の上から狙えるんじゃ・・・？
適正なホップ(m=0.20[g],20回転)の場合、2[m]位の障害物があれば上の黄色Θ=0.64°の軌道でよさそうです。
しかし、障害物を超えて1m落下するのに5[m]位離れてしまいます。なので、敵が障害物から5[m]程度離れている時に撃てば当てられますね。

2015/4/28 追）

実際の弾道のデータとの比較

BB弾の実際の飛距離をデータとして掲載しているページを見つけました。ここです↓
東京マルイ　G36CにおけるノーマルホップとG-HOPの弾道特性
測定は大変なものなので緻密なデータとはいきませんが、大体の傾向と、この計算がどのくらいよいものなのか、はわかりそうです。
BB弾の回転数は上のページを参考にし、最大到達点を目安に決定しました。
0.2gのデータは良いデータではなさそうだったのであきらめ、0.25gの結果のみで弾道の軌道を比較しましょう。
数値計算では無風状態でBB弾の重さ0.25g, 初速75m/s,高さ1.1mから射出します。
回転数はおおよそ343回転の時、最高到達点が2.4[m]程度と数値計算によって分かったためそれを使います。その時のデータは以下のようになりました。

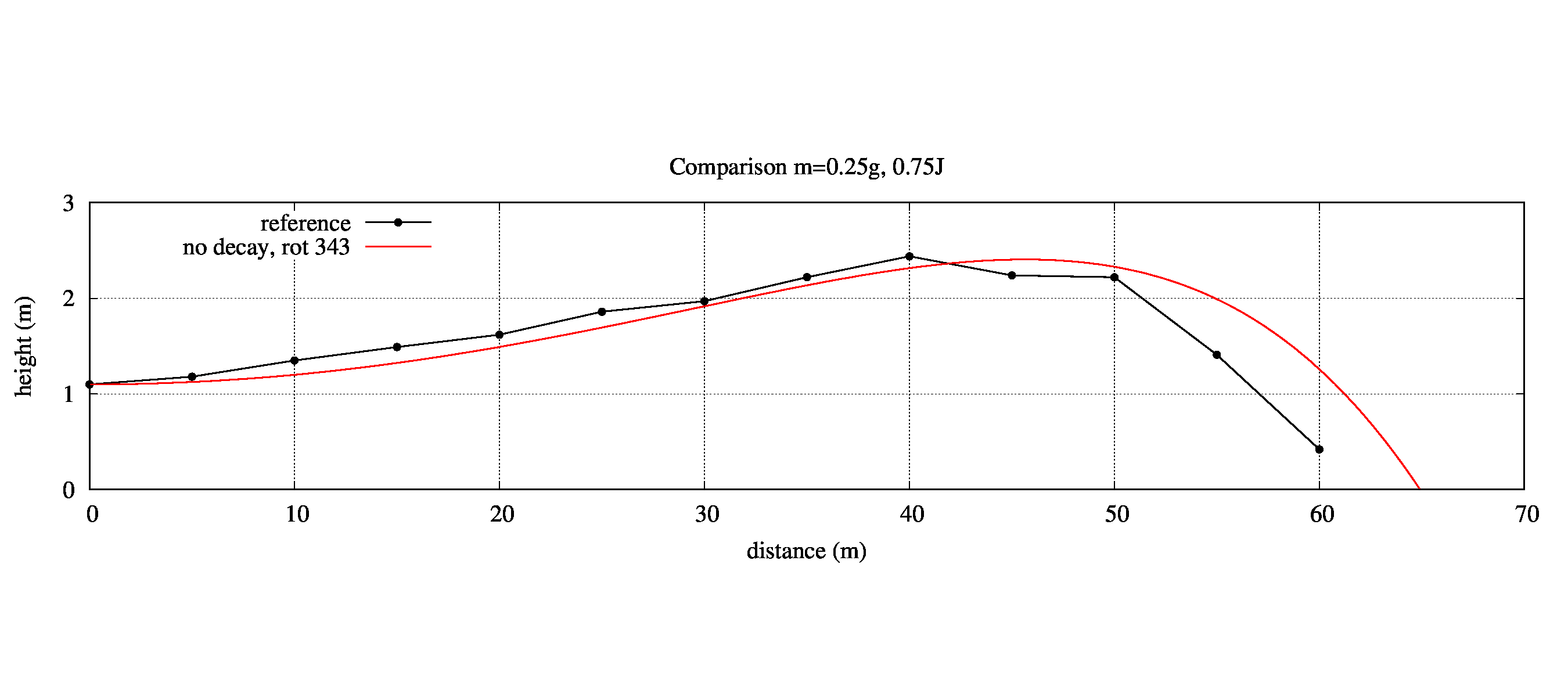
比較対象は黒色の線です。割と良い一致をしています。
原因を考察します。どの程度の統計性があるかは分かりませんが、写真を見る限り、数十発程度の平均値であろうと予想できます。
なので、毎回50m地点で向かい風が吹いて失速し、それが数値計算とのずれだ、などという状況は考えにくそうです。
一番考えられるのはBB弾の回転角速度の減衰でしょう。次の節で取り扱います。

そのほか、この計算に一致しない理由としては、温度による粘性抵抗のずれ、
若干の向かい風がある(計算よりも早くホップにより上昇しているため)、横方向の考慮、測定ミスetc…上げればきりがありません。
しかし、おおよその傾向は良いです。ホップが効いて下がり始めるまではほとんど同じ軌跡を辿っています。

ちなみに、地面に着弾するまでの時間は計算上では2.3秒程度でした。

追)2015/05/31

流体中に置かれた球体の回転の減衰

流体中に板を置けば、板は流体から力を受け、引きずられるはずです。
回転をしているのなら、回転方向とは反対の向きに力のモーメントを受け、回転が減衰するはずです。

最終的に、最初に角運動量がz軸方向の成分しかない場合、角速度の時間変化\(\frac{d\omega_z}{dt}\)は、
\(
\begin{align}
\frac{d\omega_z}{dt}&=N_z/I \\
N_z&=\frac{\rho C_f}{2}R^3\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{align}
\)
と求められます。(ここで\(I\)は慣性モーメント、\(C_f\)は摩擦抗力係数、\(u\)は物体の、風との相対速度を表します。)
これを計算し、BB弾の角速度に反映させます。

ここから自信が無いので、あっているか、物理の背景が正しいかは保証できません。
まず、回転を記述する運動方程式は、
\(
\displaystyle \frac{d\vec{L}}{dt}=\vec{N}
\)
慣性モーメント\(I\)を用いると、\(\vec{L}=I\vec{\omega}\)であるため、
\(
\begin{align}
I\frac{d\vec{\omega}}{dt}&=\vec{N} \\
I\frac{d^2\vec{\theta}}{dt^2}&=\vec{N}
\end{align}
\)
ここで\(\frac{d\vec{\theta}}{dt}=\vec{\omega}\)と置いています。

求めるべきは右辺の力のモーメント\(\vec{N}\)です。

摩擦抗力\(D_f\)、摩擦抗力係数\(C_f\)というものがありました[6,7,10]。
境界層流れ、という分野に分類されるそうです。
流れている流体に対して摩擦によって平板に生まれる、摩擦抗力\(D_f\)は
\(
\displaystyle D_f=-C_f\frac{\rho U^2}{2}S_{contact}
\)
と記述でき、\(C_f\)は摩擦抗力係数、\(\rho\mathrm{[kg\cdot m^{-3}]}\)は流体の密度、
\(U\mathrm{[m\cdot s^{-1}]}\)は流体との相対速度、\(S_{contact}\)は流体と物体の接触面積を記述しています。
\(C_f\)はレイノルズ数\(R_e\)の関数であり、
層流領域(\(R_e\lt 5\times 10^5 \sim 10^6\))では[10]
\(
\displaystyle C_f=\frac{1.328}{\sqrt{R_e}}
\)
乱流領域(\(5\times 10^{5}\lt R_e \lt 5\times 10^6\))では[6]
\(
\displaystyle C_f=\frac{0.074}{{R_e}^{1/5}}
\)
乱流領域(\(10^{7}\lt R_e\))では[6]
\(
\displaystyle C_f=\frac{0.455}{(\log_{10}{R_e})^{2.58}}
\)
を用いるのが推奨されるようです。
専門家ではないのでこれらの係数の導出等々は知りません。
エアガンの場合、レイノルズ数はおおよそ\(3\times 10^{4}\)程度なので層流領域だと見積もられます。

この摩擦抗力を元に、空気抵抗によって回転が減衰することを調べてみましょう。
ただし、ここでは２つの仮定をします。

  1. 風は角度\(\varphi, (0\le\varphi\lt 2\pi)\)のみに依存する
  2. 位置\(\vec{r}\)で速度\(\vec{v}(\vec{r})\)を持つとき、その微小面積\(\Delta S\)に働く摩擦抗力\(\Delta D_\vec{f}\)を
    \(\displaystyle \Delta D_\vec{f}=-\frac{\rho C_f}{2}|\vec{v}(\vec{r})|^2\frac{\vec{v}(\vec{r})}{|\vec{v}(\vec{r})|}\Delta S\)
    と仮定

これらの仮定の下、話を進めます。
微小区間に働く力のモーメント\(\Delta\vec{N}=\vec{r}\times \Delta\vec{f}\)を考えてから、全空間で積分を行います。
そのために位置\(\vec{r}\)の点における速度\(\vec{v}\)を導出します。
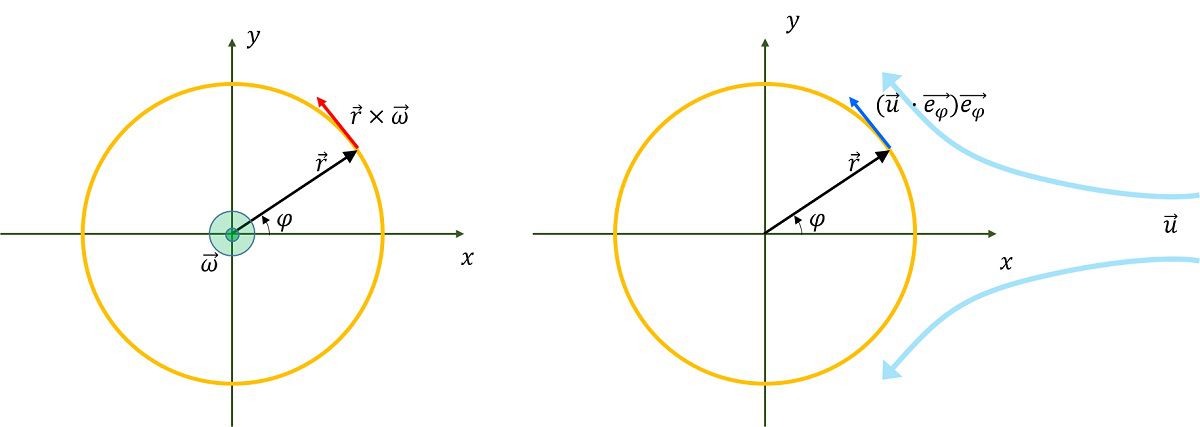
減衰_回転と風_c
摩擦抗力は相対速度\(\vec{v}\)によって記述されると考えられるので、回転によって生じる速度\(\vec{v}_{rot}\)とその地点での風の速度\(\vec{v}_{win}\)を使えば、
\(
\vec{v}=\vec{v}_{win}-\vec{v}_{rot}
\)
と書くことができます。
まず、\(\vec{v}_{rot}\)は、
\(
\vec{v}_{rot}=\vec{r}\times \vec{\omega}
\)
と表現されます。また、\(\vec{v}_{win}\)は、
\(
\vec{v}_{win}=(\vec{u}\cdot \vec{e}_{\varphi})\vec{e}_{\varphi}
\)
であると考えられます(仮定①)。ここで\(\vec{e}_{\varphi}\)は回転方向の単位ベクトルを表します。
よって、位置\(\vec{r}\)の相対速度\(\vec{v}\)は、
\(
\vec{v}=(\vec{u}\cdot \vec{e}_{\varphi})\vec{e}_{\varphi}-(\vec{r}\times \vec{\omega})
\)
となります。
微小区間に働く力のモーメント\(\Delta\vec{N}\)は、
\(
\begin{align}
\Delta\vec{N}&=\vec{r}\times \Delta\vec{f} \\
&=-\vec{r}\times\left(\frac{\rho C_f}{2}|\vec{v}|^2\frac{\vec{v}}{|\vec{v}|}\Delta S\right) \\
&=-\frac{\rho C_f}{2}|\vec{v}|(\vec{r}\times\vec{v})\Delta S
\end{align}
\)
と書かれます(仮定②を使用)。
今、3次元極座標を考えて積分すると位置\(R\)での微小面積はヤコビアンより、\(R^2\sin(\theta)d\varphi d\theta\)なので、
(動径方向は\(r=R\)のみ)、
\(
\displaystyle \vec{N}=-\frac{\rho C_f}{2}R^2 \int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |\vec{v}|\cdot(\vec{r}\times\vec{v}) \sin{\theta}
\)
と表せます。
あとはこれを解いて剛体の運動方程式に当てはめれば、回転の減衰が表せます。

具体的な形を当てはめていきましょう。
半径\(R\)の球体に対して、3次元極座標で考えます。すると、位置\(\vec{r}\)は、
\(
\vec{r}=
\left( \begin{array}{c}
R\sin\theta \cos\varphi \\
R\sin\theta \sin\varphi \\
R\cos\theta
\end{array} \right)
\)
であり、回転方向の単位ベクトル\(\vec{e}_{\varphi}\)は、
\(
\vec{e}_{\varphi}=
\left( \begin{array}{c}
-\sin\varphi \\
\cos\varphi \\
0
\end{array} \right)
\)
です。
回転角速度\(\vec{\omega}=(0,0,\omega)\)、風の方向\(\vec{u}=(u,0,0)\)
であると考えれば、
\(
\vec{r}\times \vec{\omega}=
\left( \begin{array}{c}
R\omega \sin\theta\sin\varphi \\
-R\omega \sin\theta\cos\varphi \\
0
\end{array} \right)
\)
であり、
\(
(\vec{u}\cdot \vec{e}_{\varphi})\vec{e}_{\varphi}=
\left( \begin{array}{c}
u \sin\varphi\sin\varphi \\
-u \sin\varphi\cos\varphi \\
0
\end{array} \right)
\)
となります。よって、相対速度\(\vec{v}\)は
\(
\vec{v}=(\vec{u}\cdot \vec{e}_{\varphi})\vec{e}_{\varphi}-(\vec{r}\times \vec{\omega})=
\left( \begin{array}{c}
(u\sin\varphi-R\omega\sin\theta)\sin\varphi \\
-(u\sin\varphi-R\omega\sin\theta)\cos\varphi \\
0
\end{array} \right)
\)
と計算できます。
故に、\(\vec{r}\times\vec{v}\)は、
\(
\vec{r}\times\vec{v}=
\left( \begin{array}{c}
R\cos\theta(u\sin\varphi-R\omega\sin\theta)\cos\varphi \\
R\cos\theta(u\sin\varphi-R\omega\sin\theta)\sin\varphi \\
-R\sin\theta(u\sin\varphi-R\omega\sin\theta)
\end{array} \right)
\)
です。
具体的に、球体に働く力のモーメント\(\vec{N}\)を求めるためにやらなければならない積分は、
\(
\displaystyle \vec{N}=-\frac{\rho C_f}{2}R^2\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta|\vec{v}|(\vec{r}\times\vec{v})\sin\theta \\
\displaystyle =-\frac{\rho C_f}{2}R^2
\left( \begin{array}{c}
R\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin\theta\cos\theta\cos\varphi \\
R\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin\theta\cos\theta\sin\varphi \\
-R\int_0^{2\pi}d\varphi\int_0^{\pi}d\theta |u\sin\varphi-R\omega\sin\theta|(u\sin\varphi-R\omega\sin\theta)\sin^2\theta
\end{array} \right)
\)
です。まず絶対値の符号を取るために場合分けを行います。
\(
|u\sin\varphi-R\omega\sin\theta| \\
=|R\omega|\cdot|\frac{u}{R\omega}\sin{\varphi}-\sin\theta|
\)
は、\(\frac{u}{R\omega}\sin{\varphi}\)に関して3つの領域に分けられます。

  1. \(\displaystyle \frac{u}{R\omega}\sin{\varphi}\le 0\)の領域
  2. \(\displaystyle 0\lt \frac{u}{R\omega}\sin{\varphi}\lt 1\)の領域
  3. \(\displaystyle 1\le \frac{u}{R\omega}\sin{\varphi}\)の領域

です。

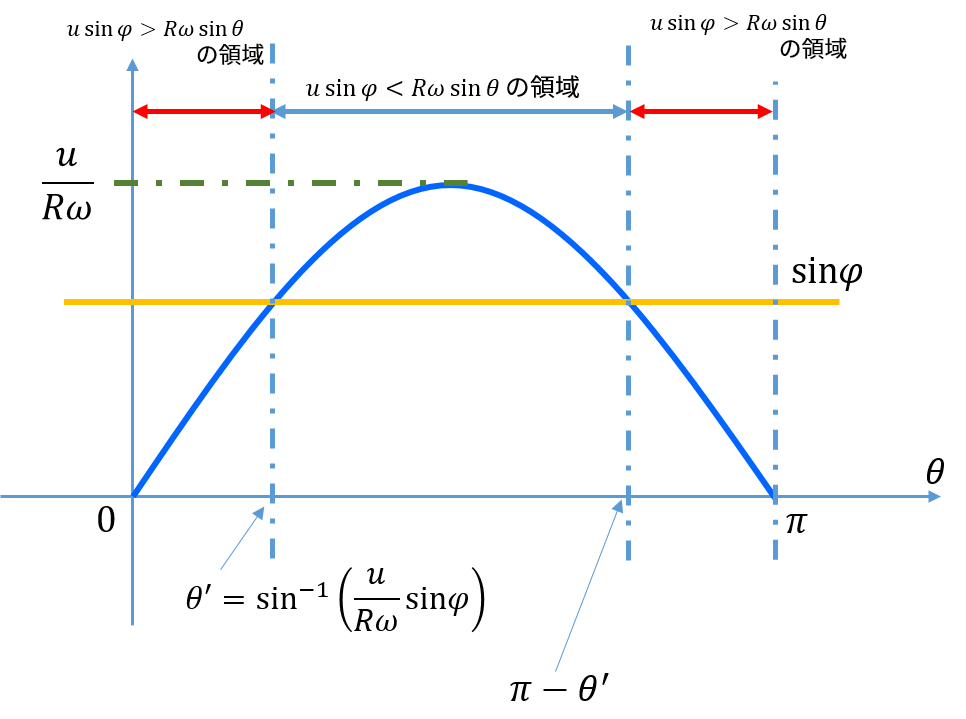
\(0\lt \frac{u}{R\omega}\sin{\varphi}\lt 1\)が厄介なので特に考えましょう。
\(|\vec{v}|=|u\sin\varphi-R\omega\sin\theta|\)に対して、図のように考えます。
場合分け

例えば力のモーメントのx成分の積分は
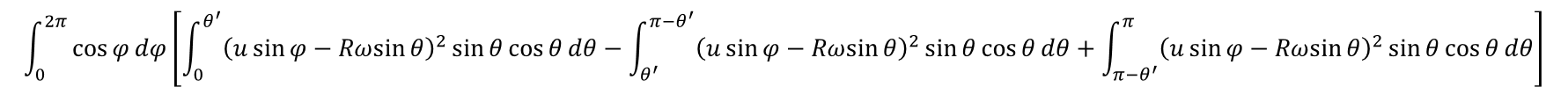
場合分け_積分
となります。

こう表したのですが、x,y成分の被積分関数は\(\pi/2\)を中心に奇関数です。z成分だけは\(\pi/2\)を中心に偶関数となります。
なのでx,y成分は計算するまでもなくゼロになり、z成分だけ残ります。
これはもともとの回転角速度\(\omega\)がz成分しか持っていないから、という概要に合っています。

z成分の\(\theta\)に関する積分までは求めました。
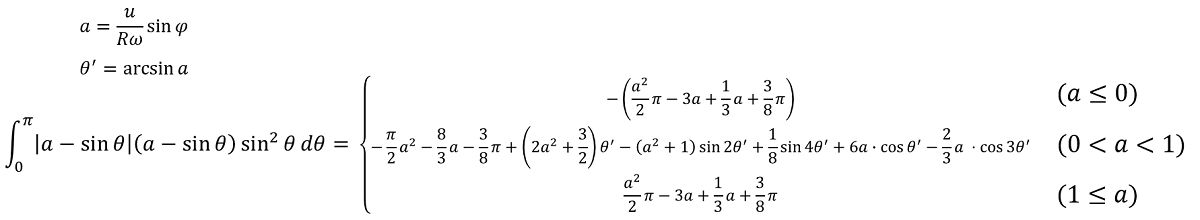
シータ方向z成分_c
となります。
この後更に\(\varphi\)でこれを積分するのですが、僕はできませんでした。多分楕円積分に近いものが必要になるかと式の形から思われます。
\(\varphi\)方向に関しては数値計算でやってしまおうと思います。

2016/08/07追）
上記積分を近似して簡略化します。
回転している球体を上半分と下半分に分けて、球体を2つの平面に近似してしまいます。
上半分の速度\(v_{up}/latexと下半分の速度[latex]v_{down}/latexはそれぞれ
[latex]
\begin{align}
v_{up}&=u\sin_{\varphi_c}-R\omega\sin_{\theta_c} \\
v_{down}&=-u\sin_{\varphi_c}-R\omega\sin_{\theta_c}
\end{align}
\)
と書けます。ここで、\(\varphi_c,\theta_c\)は球を近似するに最適なある特定の角度を表します。
すると、近似した力のモーメントは
\(
\displaystyle N=\frac{\rho C_f}{2}R\frac{4\pi R^2}{2}\left(|v_{up}|v_{up}+|v_{down}|v_{down}\right)
\)
と導くことが出来ます。

実際の弾道のデータとの比較(回転の減衰考慮)

2015/06/07追記）
2021/08/11変更）
数値計算によって\(\varphi\)方向の数値計算を行い、比較してみます。

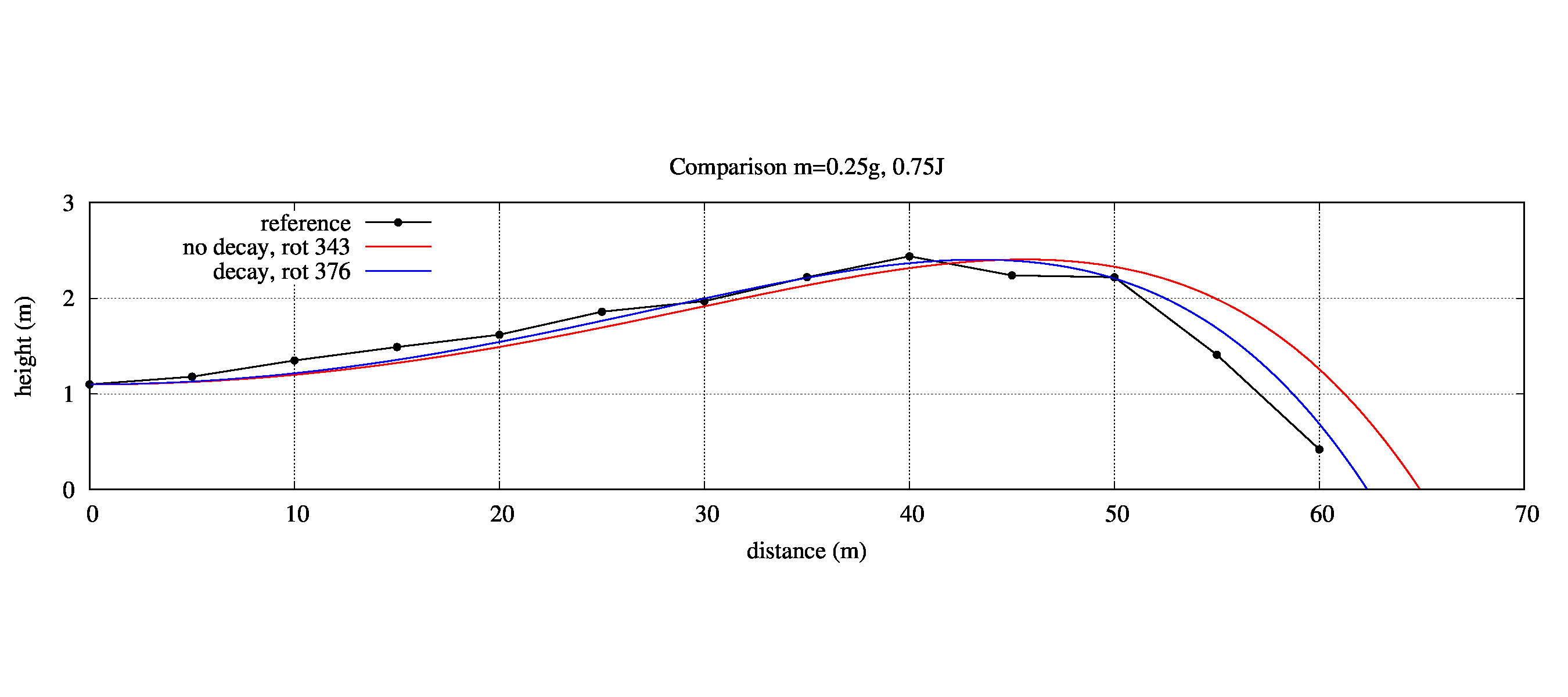
左図中の横軸は球の進行方向を表し、縦軸は高さを表します。
黒は参考とした実測データ、青は回転の減衰の効果を計算に入れない時、赤は回転の減衰を入れた時です。
回転数は、最大到達高さが2.4mになるような値を用いています。

回転の減衰を考慮に入れた計算結果は青の線です。
素晴らしいですね。最高です！
回転の減衰によってMagnus力が減少し、到達距離が短くなっています。
以前の計算結果である赤線の時に問題になった、最後のあたりのBB弾の伸びが違う、といった辺りがちゃんと改善されました。

なぜ質量が軽いほうが回転の減衰が早いのでしょうか？
今回の回転の減衰の導出では、表面積によってのみ、回転の減衰を引き起こす力のモーメントが変化します。なので、質量が重ければ思いほど、その分慣性モーメント\(I\)が大きいことになり、回転量は変化しにくいことになります。

[adsense2]

ちなみに、Magnus力のする仕事はゼロです。
なぜなら、Magnus力の働く方向は粒子の速度に垂直なはずで、方向は\(\vec{v}\times \vec{\omega}\)です。
その仕事は、係数を無視して、
\(
\begin{align}
&\int_{\vec{r}_{(t)}}^{\vec{r}_{(t+\Delta t)}}(\vec{v}\times\vec{\omega})\cdot d\vec{r} \\
&=\int_t^{t+\Delta t} (\vec{v}\times\vec{\omega})\cdot \vec{v} dt \\
&=\int_t^{t+\Delta t} 0{dt}
&=0
\end{align}
\)
となるからです。
・・・ということは、Magnus力が仕事をすることはあり得ません。

fortran90によるコードはこちらへ↓
弾道計算(BB弾)のコード

参考文献

[1]伊東敏雄著『な～るほど!の力学』学術図書出版社 (1994) p.220
[2]Faith A. Morrison, “Data Correlation for Drag Coefficient for Sphere,” Department of Chemical Engineering, Michigan Technological University, Houghton, MI (2015/02/08 アクセス確認)
[3]NASA, Ideal Lift of a Spinning Ball(2015/02/08 アクセス確認)
[4]国立天文台編『理科年表 平成21年 第82冊』丸善株式会社 (2009) p.378
[5]国立天文台編『理科年表 平成21年 第82冊』丸善株式会社 (2009) p.376

[6]第9章 境界層と物体まわりの流れ
[7]Skin friction drag

[8]流体力学講話・つまみ食い（その５）

[9]鳴尾 丈司, 溝田 武人, 下園 仁志, “一様気流中で高速回転するゴルフボールの空気力測定と飛しょう実験” 日本機械学会論文集 B編 Vol. 70 (2004) No. 697 P 2371-2377

[10]第3章 境界層理論, 3.5.4摩擦抵抗係数 \(C_{D_f}\)

[11]石岡、ホップアップの回転数測定　TM VSR-10 G-SPEC

[12]放物運動 -初等力学の未解決問題：速度の２乗に比例する空気抵抗を持つ放物運動

gnuplot

裏面の色と隠線処理

コメントする

gnuplotの通常の表示では隠れて見えない部分も見せようとします。
例えば手前に大きな山があり、後ろは見えないはずですが、格子状にしているとそれが見えてしまいます。表示させないようにするには、

set hidden3d

とすればokです。

set hidden3dをする

hidden3dの効果

また、3D表示において裏面と表面の色を変えたい時は、

set hidden3d back offset 1 trianglepattern 3 undefined 1 altdiagonal bentover

とすればいいです。参考URLの値そのままです。

例えば上の数字のところを変えれば裏面の色を変えることができます。

set hidden3d back offset 2 trianglepattern 3 undefined 1 altdiagonal bentover

とすれば、
hidden3d裏面の色

gnuplot demo script: surface2.demより。