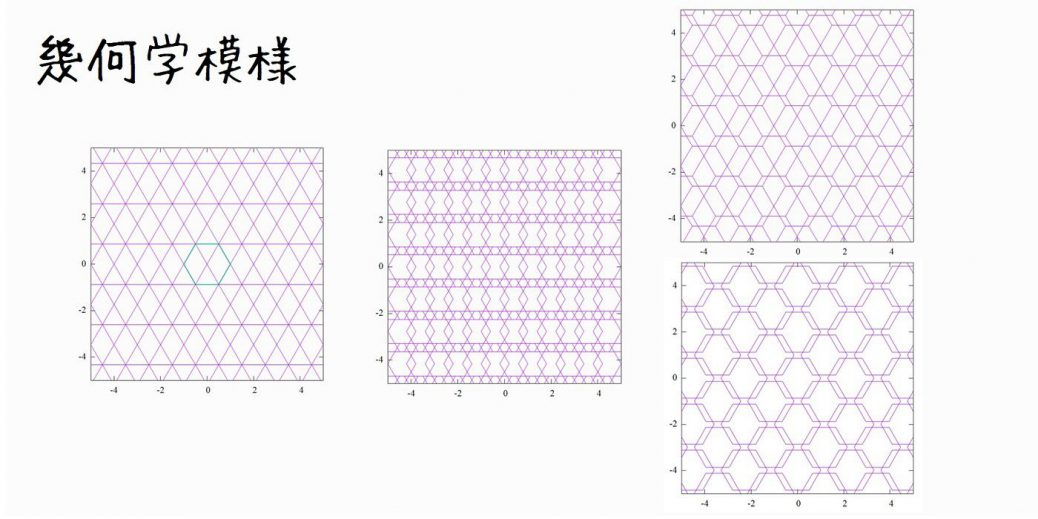
gnuplotで幾何学模様を描きます。
正多角形の組み合わせで幾何学模様を描きます。
gnuplot version5.0以上でないと動きません。
用いるのは正多角形の数式
\(
\begin{equation}
\left\{
\begin{aligned}
x&\displaystyle =\cos t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}\\
y&\displaystyle =\sin t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}
\end{aligned}
\right.
\end{equation}
\)
です。ここで、\(a_n=\frac{2\pi}{n}\)、\({\rm floor}(x)\)は床関数(床関数と天井関数)であり、媒介変数\(t\)の範囲は(\(0\le t \lt 2\pi\))です。
正六角形を特に考えましょう。以下のスクリプトを実行することで
set param
set xr[-5:5]
set yr[-5:5]
set tr[0:2*pi]
unset key
set size ratio -1
n=6
# +---polygon---+
s1(x)=x-floor(x)
a(n)=2e0*pi/real(n)
cnp(n,t)=cos(a(n)*s1(t/a(n))-0.5e0*a(n))
pc(n,t)=cos(t)*cos(0.5e0*a(n))/cnp(n,t)
ps(n,t)=sin(t)*cos(0.5e0*a(n))/cnp(n,t)
set samples n*3+1
# +--- geometric pattern ---+
nr=1e0
ix=6
jy=6
xc=0e0
yc=0e0
xr=1e0
yr=sqrt(3e0)
oddshift=0e0
plot for[i=-ix:ix]for[j=-jy:jy] \
nr*pc(n,t)+xr*i+xc,\
((i+ix)%2 == 1 ? nr*ps(n,t)+yr*j+oddshift+yc : nr*ps(n,t)+yr*j+yc) lc 1
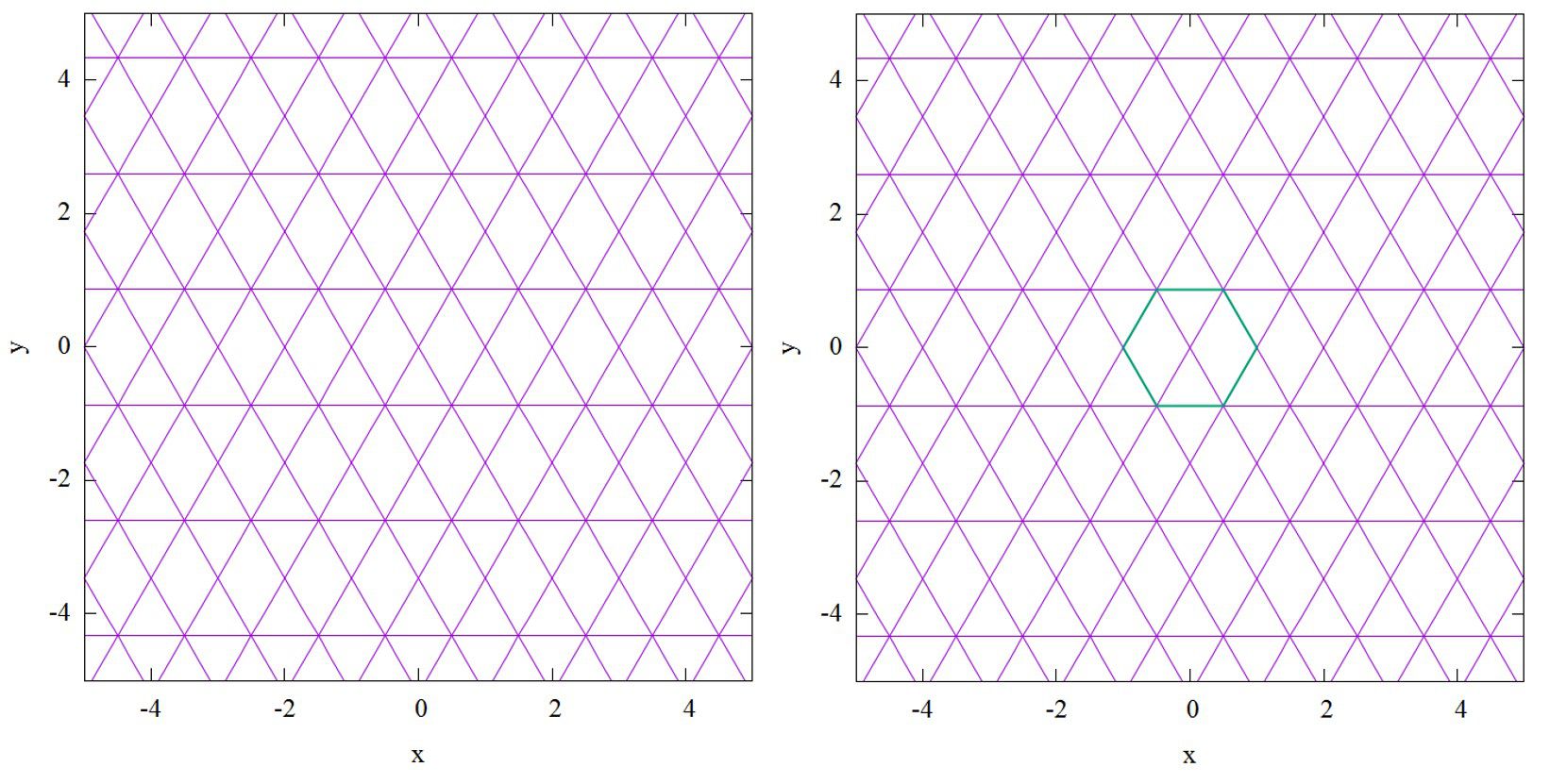
という画像が得られます。
これは、正六角形の組み合わせで作られており、それを格子状に配置することで幾何学模様を作り出しています。
格子点の配置や正六角形の大きさを変更することで様々な幾何学模様が得られます。
上記スクリプトの変数はそれぞれ
————————-
nr : 正n角形の大きさ(比率)
jx : 格子の列数の半分
jy : 格子の行数の半分
xc : x方向の格子のオフセット
yc : y方向の格子のオフセット
xr : x方向の格子の間隔
yr : y方向の格子の間隔
oddshift : x方向の奇数番目の列に対するy方向のオフセット
————————-
以下はxr,yr,oddshiftの組み合わせによって得られる様々な幾何学模様のパターンです。
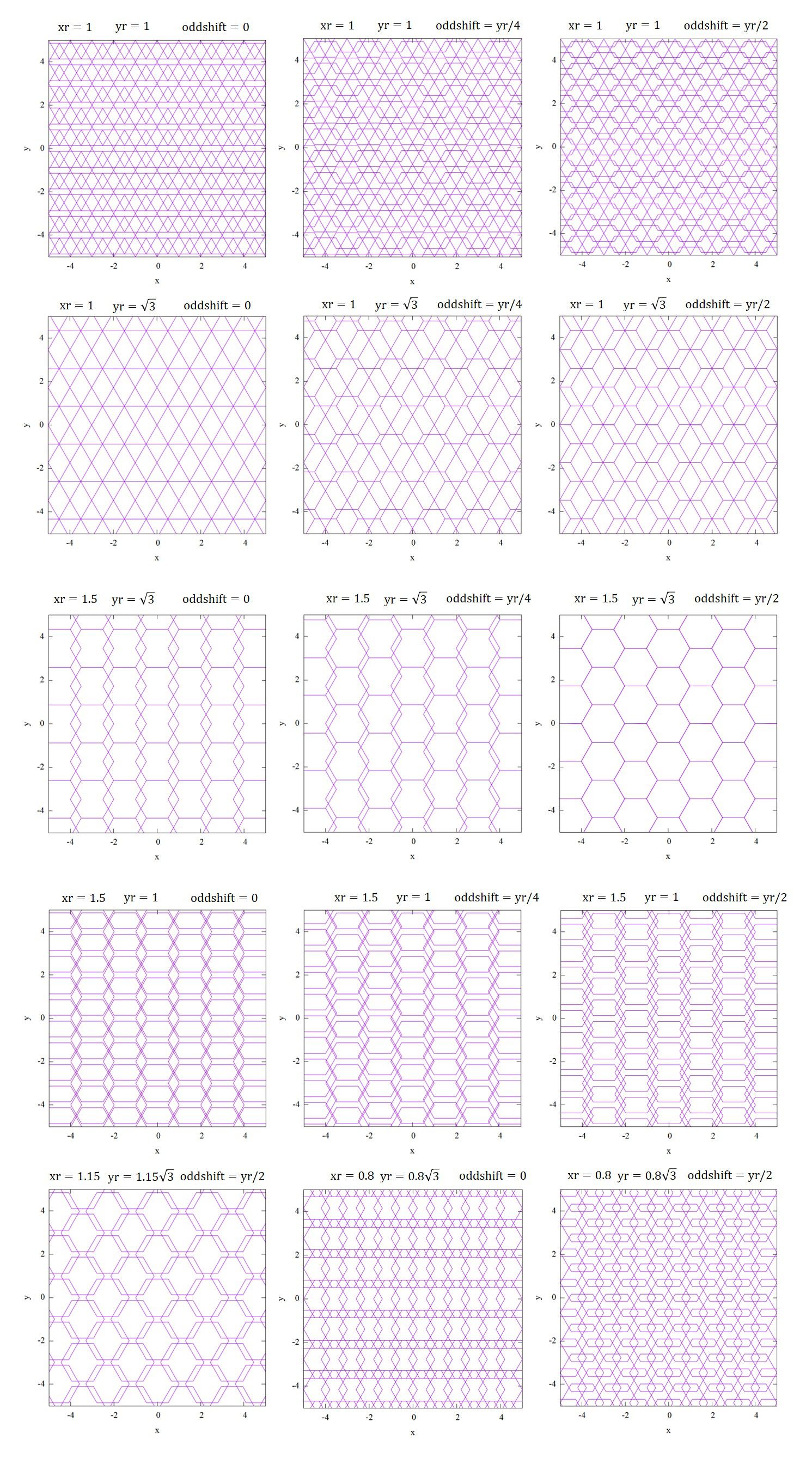
グラフェンっぽいのができますね。
3次元に簡単に拡張できるので、炭素の構造とかも作れます。
もちろん回転させることも可能です。
その場合はスクリプト”setting pattern”以下を
# +--- setting pattern ---+
nr=1e0
ix=6
jy=6
xc=0e0
yc=0e0
xr=1e0
yr=1e0
oddshift=yr/2e0
theta=pi/2e0
plot for[i=-ix:ix]for[j=-jy:jy] \
((i+ix)%2 == 1 ? pc(n,t)*cos(theta)-ps(n,t)*sin(theta)+xr*i+xc : pc(n,t)+xr*i+xc),\
((i+ix)%2 == 1 ? pc(n,t)*sin(theta)+ps(n,t)*cos(theta)+yr*j+yc+oddshift : ps(n,t)+yr*j+yc) lc 1
と変更してください。これは奇数列目のみを回転させる操作です。
適当なパラメータにおいて、
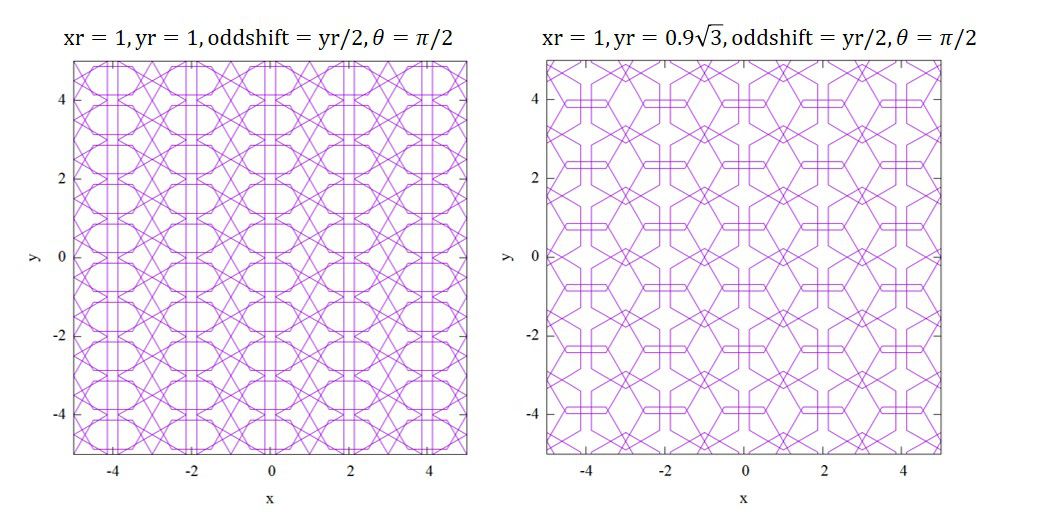
という模様が得られます。
また、正n角形全てのパターンを考える事が出来ます。例えば、正七角形の場合、
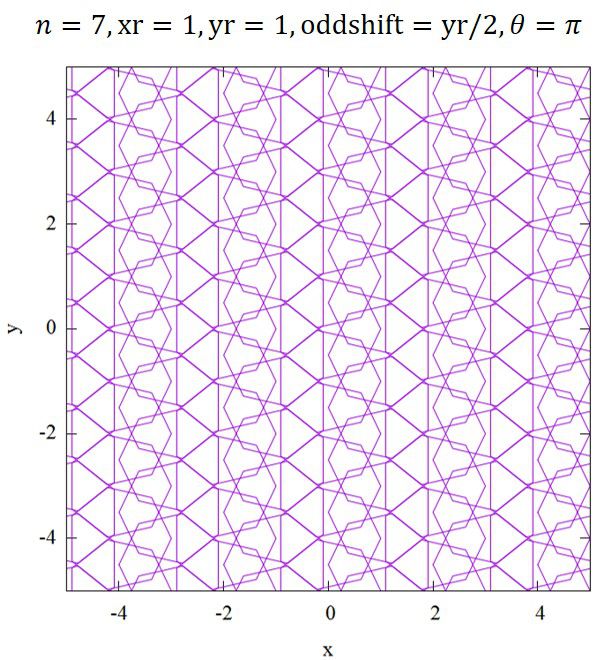
といった模様が得られます。