1. 結論 #

ある一つの真の値 $X$ を得たい時、複数回の測定値 $x_1, x_2,\cdots, x_N$ から真の値を得ようと考えます。

この時、真の値$X$は不確かさを含めて下記の通りに推定します。

$$ \begin{align} \label{eq1} X \to \bar{x} \pm \Delta\bar{x} \end{align} $$

ここで、$\bar{x}$は$x_1, x_2,\cdots, x_N$の最確値（または平均値）, $\Delta\bar{x}$は最確値の不確かさで下記の通り与えられます。

$$ \begin{align} \bar{x} &= \frac{1}{N}\sum_{i=1}^N x_i \label{eq2}\\ \Delta\bar{x} &= \frac{\Delta x}{\sqrt{N}}=\frac{1}{{\sqrt{N}}}\sqrt{\frac{1}{N-1}\sum_{i=1}^N (x_i-\bar{x})^2} \label{eq3} \end{align} $$

“不確かさ” の意味は、測定値が真の値を中心に純粋に確率的にばらつくと仮定した場合に、真の値が$\bar{x}\pm \Delta\bar{x}$の間にある確率が約68.3% (いわゆる$1\sigma$の範囲内) であることを意味します。

式\eqref{eq3}から分かる不確かさの重要な性質として、不確かさを$1/10$にしたい場合、そのデータ総数を100倍にする必要があります。

2. 説明 #

ガウスの誤差理論に従って議論します¹²。 つまり、測定値のばらつきは純粋に確率的であると仮定して話を進めます。 もう少し具体的に言うと、測定値は真の値$X$を中心としたガウス分布の確率分布$p(x)$に従う、と考えます。

つまり、確率分布$p(x)$は下記の形をしています。

$$ \begin{align} \label{eq4} p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp{\left[-\frac{1}{2}\left(\frac{x-X}{\sigma}\right)^2\right]} \end{align} $$

$$ \begin{align} \label{eq5} \int_{-\infty}^{\infty} p(x) dx=1 \end{align} $$

ここで、$\sigma$は標準偏差、$\sigma^2$は分散を示します。

2.1. 最確値$\bar{x}$の導出 #

最確値は、測定対象の最も確からしい値という意味があります。これを確率分布$p(x)$に従う確率で得られる測定結果から計算することを考えましょう。

確率分布$p(x)$を持つ対象に対して測定値$x_i$を得る確率は$p(x_i)$です。 複数の測定で結果 $x_1, x_2, \cdots, x_N$ を得る確率はそれぞれの確率の積で書けるので、その確率は下記のように書けます。

$$ \begin{align} \label{eq6} p(x_1)p(x_2)\cdots p(x_N) &\propto \prod_{i=1}^N \exp{\left[-\frac{1}{2}\left(\frac{x_i-X}{\sigma}\right)^2\right]} \\ &=\exp{\left[-\frac{1}{2\sigma^2}\sum_{i=1}^N\left(x_i-X\right)^2\right]} \label{eq7} \end{align} $$

現実的に複数回の測定を行った場合、それは式\eqref{eq7}を最も大きくする組み合わせが得られるのだと考え、その仮定から$X$を決めます。 それはつまり式\eqref{eq7}が最も大きい、つまり

$$ \begin{align} \label{eq8} \sum_{i=1}^N\left(x_i-X\right)^2 \end{align} $$

を最小にする$X$を測定${x_i}$から得られる測定対象の最も確からしい値、すなわち最確値として採用します。\eqref{eq8}の極値をとる時、その$X$による微分が0になると予想できます。なので、

$$ \begin{align} \label{eq9} \frac{\partial}{\partial X}\sum_{i=1}^N\left(x_i-X\right)^2 = -2\sum_{i=1}^N\left(x_i-X\right) \\ \sum_{i=1}^N\left(x_i-X\right)\Bigr|_{X=X_0}=0 \end{align} $$

が満たされる$X=X_0$が最確値とします。以上から、

$$ \begin{gather} \label{eq10} \sum_{i=1}^N \left(x_i-X_0 \right)=0 \\ \sum_{i=1}^N x_i-N X_0 =0 \\ \to X_0 = \bar{x}\equiv \frac{1}{N}\sum_{i=1}^N x_i \end{gather} $$

を得ます。これはつまり、最確値$X_0$は複数の測定値${x_i}$の算術平均として求められるということです。

2.2. 最確値の不確かさ$\Delta\bar{x}$の導出 #

続いて、測定の不確かさ（ばらつき）を考えます。 ガウス分布を考えているので、標準偏差である$\sigma$を測定値${x_i}$を用いて表現することができればよいと考えます。

$\sigma$は真の値$X$が分かっているときに式\eqref{eq11}に従って求めることができます。

$$ \begin{align} \label{eq11} \sigma^2 = \frac{1}{N}\sum_{i=1}^N (x_i-X)^2 \end{align} $$

ただし、真の値$X$は今分からないので、その状況下で求めることを考えましょう。
ここで、$\sigma$は根号が入っており扱いが面倒であるため、2乗である分散を考えています。

ここまでの議論で、最確値$X_0$は${x_i}$の算術平均$\bar{x}$で良いという結論になったので、これを絡めて式\eqref{eq11}に含まれる和を変形していきます。 天下り的ですが、下記のように平均$\bar{x}$を登場させます。

$$ \begin{align} \sum_{i=1}^N (x_i-X)^2 &=\sum_{i=1}^N \left[{(x_i-\bar{x})+(\bar{x}-X)}\right]^2 \label{eq13}\\ &= \sum_{i=1}^N (x_i-\bar{x})^2 + \sum_{i=1}^N(\bar{x}-X)^2+ 2(\bar{x}-X)\sum_{i=1}^N (x_i-\bar{x}) \label{eq14}\\ &= \sum_{i=1}^N (x_i-\bar{x})^2 + N(\bar{x}-X)^2 \label{eq15} \\ &= \sum_{i=1}^N (x_i-\bar{x})^2 + \frac{1}{N}\left[\sum_{i=1}^N(x_i-X)\right]^2 \label{eq16} \\ &= \sum_{i=1}^N (x_i-\bar{x})^2 + \frac{1}{N}\sum_{i=1}^N(x_i-X)^2+ \frac{1}{N}{\sum\sum}_{i\ne j}(x_i-X)(x_j-X) \label{eq17}\\ &\approx \sum_{i=1}^N (x_i-\bar{x})^2 + \frac{1}{N}\sum_{i=1}^N(x_i-X)^2 \label{eq18} \end{align} $$

ここで、式\eqref{eq14}の第三項は平均値の定義なのでゼロとなります。式\eqref{eq17}から式\eqref{eq18}において、${\sum\sum}_{i\ne j}(x_i-X)(x_j-X)$を無視しました。これは必ず正になる$\sum_{i=1}^N(x_i-X)^2$とは異なり正または負を取りえ、更に異なる確率同士の積の和なのでゼロに近くなることが予想できます。

数値実験をした例を下記に示します。

	平均$\mu=0$, 分散$\sigma=3$のガウス分布に対する式\eqref{eq17}の各項の値
全体像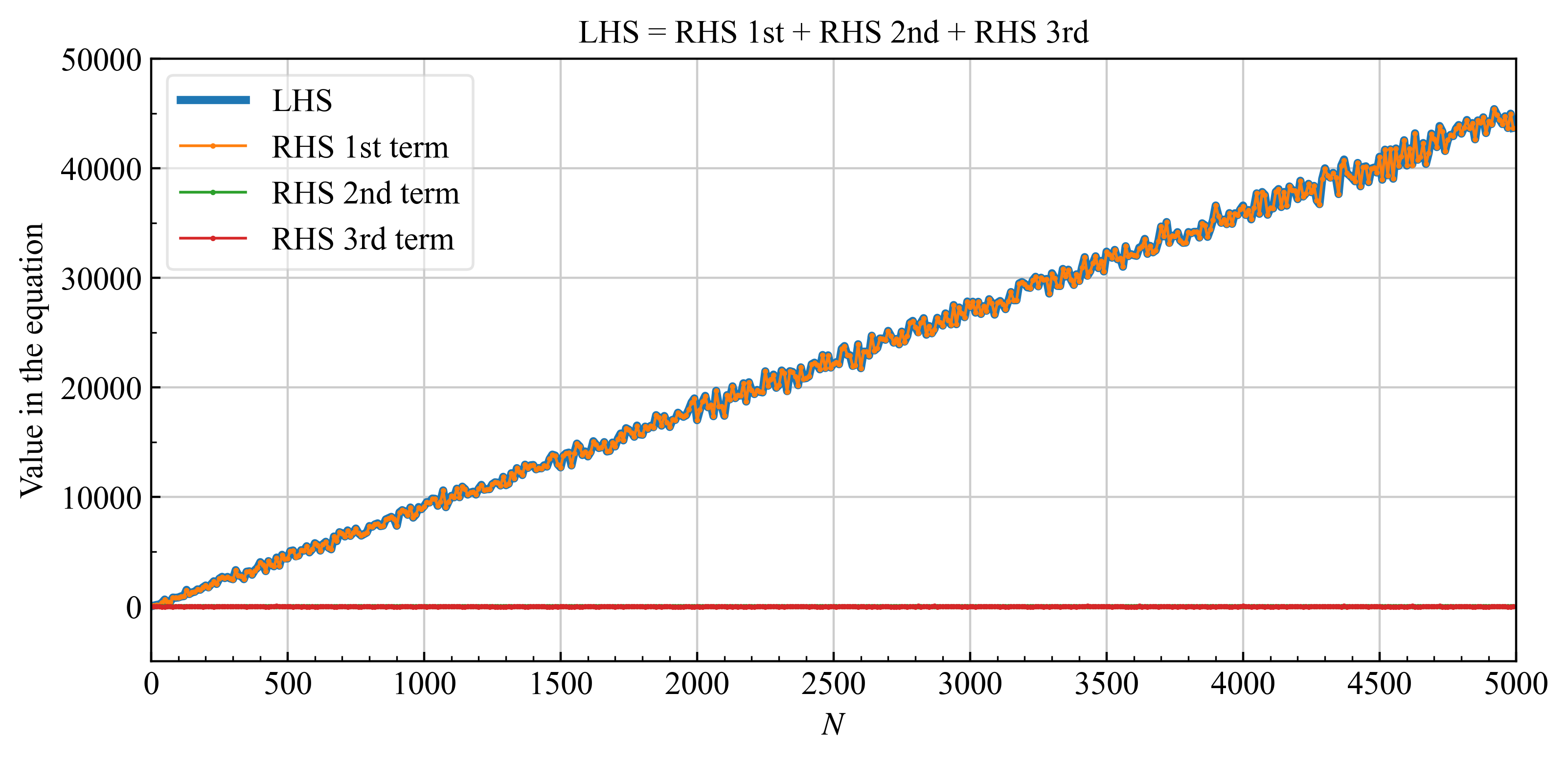
拡大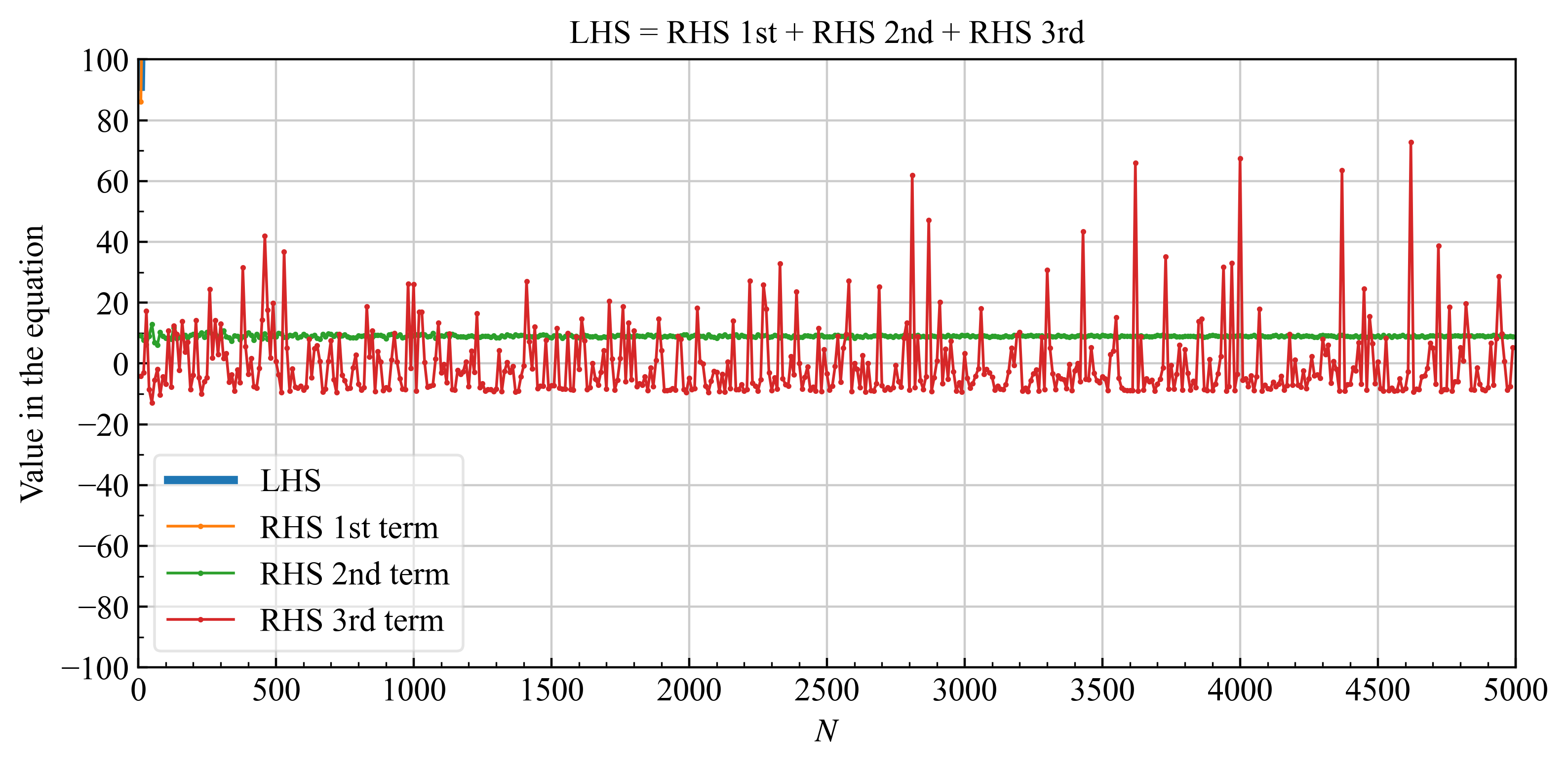

式\eqref{eq18}の第3項を示す赤線は、時々、第2項よりも大きくなる時があるので無視するという近似は使用できないと思うかもしれません。 しかし、第2項、第3項は結局真の値$X$が分からないと評価できないため、期待値として考えるべきです。そのため、第2,3項の期待値を項の値として考えると第2項はある程度の値（上図では約10）, 第3項は0になると考えられます。そのため、式\eqref{eq17}から式\eqref{eq18}にかけて第3項を無視する近似が可能です。

式\eqref{eq18}について、本来求めたかった$\sigma^2=\frac{1}{N}\sum_{i=1}^N (x_i-X)^2$について解けば、関係式

$$ \begin{align} \sigma^2&=\frac{1}{N}\sum_{i=1}^N (x_i-X)^2 \label{eq19} \\ &\approx \frac{1}{N-1}\sum_{i=1}^N (x_i-\bar{x})^2 \label{eq20} \end{align} $$

を得ます。通常、左辺を標準偏差、右辺を不偏標準偏差として区別します。真の値が分からないときは、式\eqref{eq19}の右辺に従って計算しなければなりません。

さて、式\eqref{eq20}より得られる不確かさ$\Delta x=\sigma$は、それぞれの測定$x_i$の不確かさであって、最確値$\bar{x}$の不確かさではない事に注意してください。 最確値$\bar{x}$の不確かさ$\Delta \bar{x}$は、次のように求められます。

$\bar{x}$は${x_i}$の算術平均でした。再掲しますと下記のようになります。

$$ \begin{align} \bar{x} = \frac{1}{N}\sum_{i=1}^N x_i \label{eq21} \end{align} $$

一般に、$f=f(x,y,z,\cdots)$と書かれる関数のそれぞれの引数$x,y,z, \cdots$に不確かさ$\Delta x, \Delta y, \Delta z, \cdots$を持つ場合、$f$の不確かさ$\Delta f$は

$$ \begin{align} \Delta f = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2(\Delta x)^2+\left(\frac{\partial f}{\partial y}\right)^2(\Delta y)^2+\left(\frac{\partial f}{\partial z}\right)^2(\Delta z)^2+\cdots} \label{eq22} \end{align} $$

として与えられます。ここで、偏微分はそれぞれの変数$x,y,z\cdots$の最確値$\bar{x},\bar{y},\bar{z},\cdots$です。これは、最確値周りで解を直線近似（一次までのテーラー展開）を仮定して不確かさ\eqref{eq20}を考えれば得られます。

最確値$\eqref{eq21}$に対して式\eqref{eq22}を適用すると、最確値の不確かさ$\Delta\bar{x}$は

$$ \begin{align} \Delta \bar{x} &= \sqrt{\left(\frac{\partial \bar{x}}{\partial x_1}\right)^2(\Delta x_1)^2 + \left(\frac{\partial \bar{x}}{\partial x_2}\right)^2(\Delta x_2)^2+\cdots} \\ &= \sqrt{\frac{1}{N^2}\sigma^2 + \frac{1}{N^2}\sigma^2 + \cdots + } \\ &= \frac{\sigma}{\sqrt{N}}\label{eq23} \end{align} $$

と計算されます。ここで$\frac{\partial \bar{x}}{\partial x_j} = \frac{1}{N}$を用いました。

2.3. まとめ #

以上より、複数回の測定値 $x_1, x_2,\cdots, x_N$ から最も確からしい最確値は、不確かさを含め

$$ \begin{align} \bar{x} \pm \Delta\bar{x} \end{align} $$

と与えられます。ここで$\bar{x}$は最確値（または平均値）、 $\Delta\bar{x}$は最確値の不確かさで下記の通り与えられます。

$$ \begin{align} \bar{x} &= \frac{1}{N}\sum_{i=1}^N x_i\\ \Delta\bar{x} &= \frac{\Delta x}{\sqrt{N}}=\frac{1}{{\sqrt{N}}}\sqrt{\frac{1}{N-1}\sum_{i=1}^N (x_i-\bar{x})^2} \end{align} $$

不確かさは、この範囲に真の値が含まれる確率が約68.3% (いわゆる$1\sigma$の範囲内) であることを意味します。

3. 数値実験 #

3.1. 例 #

平均$\mu=0$, 偏差$\sigma=3$を持つ正規分布に従う乱数を発生させ、この答えを持っている状態で発生させたデータを解析し、最確値（平均値）とその不確かさを推定します。 具体的な分布は下図の通りです。

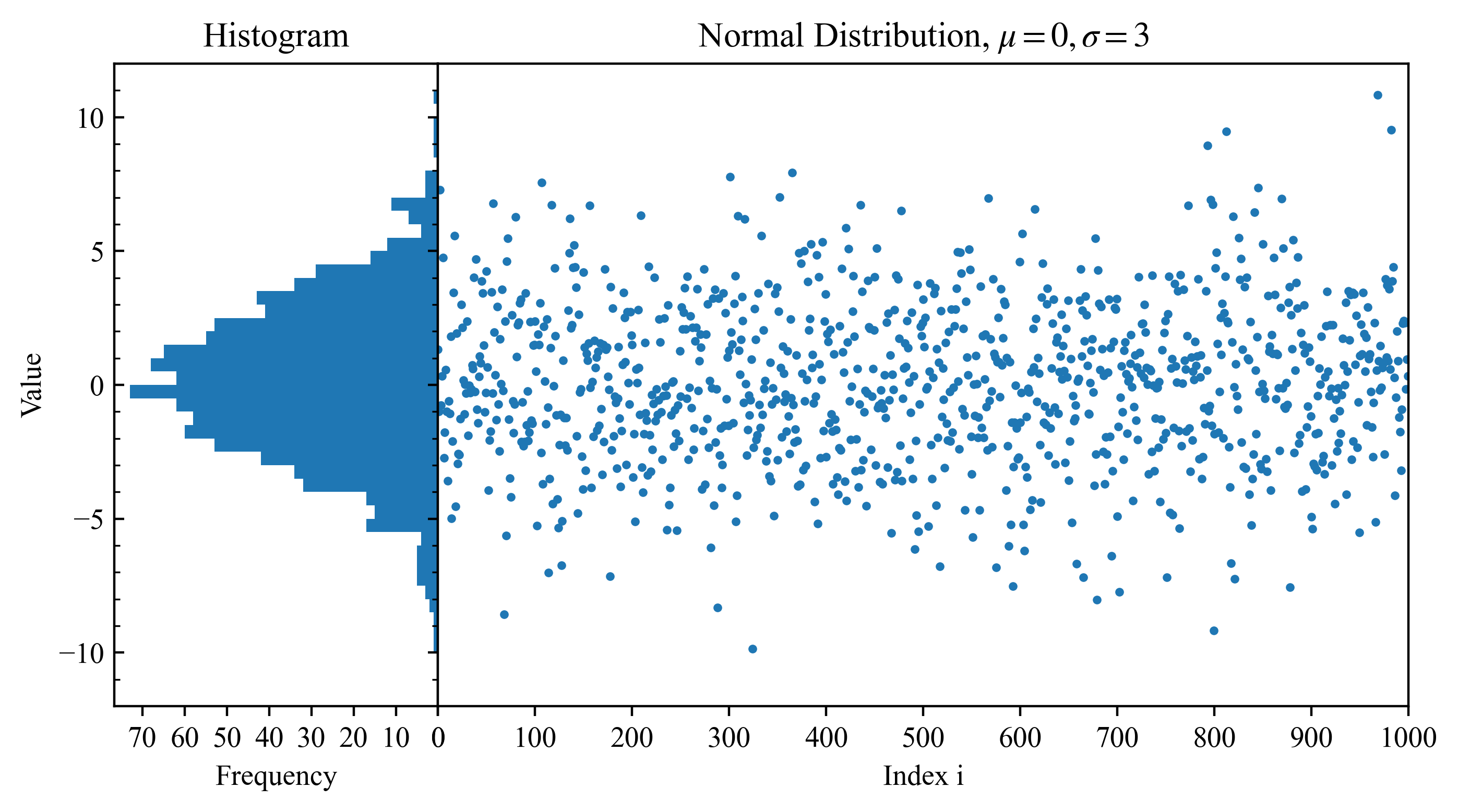
上図のデータはpythonプログラムにおいて、samples = np.random.normal(mu, sigma, N)に従って生成したデータです。

3.2. $N\leq 100$の場合（刻み幅1） #

3.2.1. 偏差・不確かさ #

偏差	不確かさ
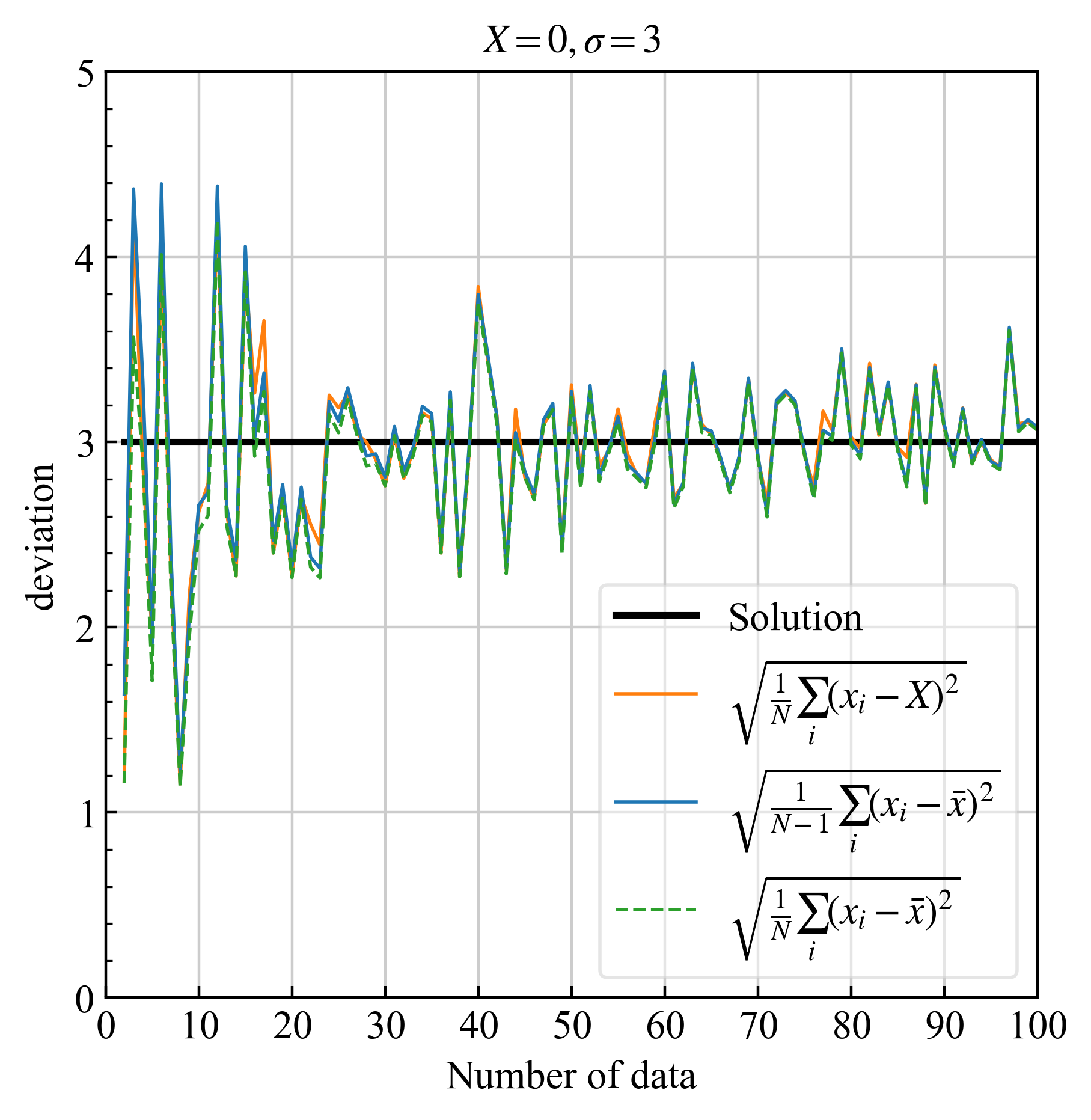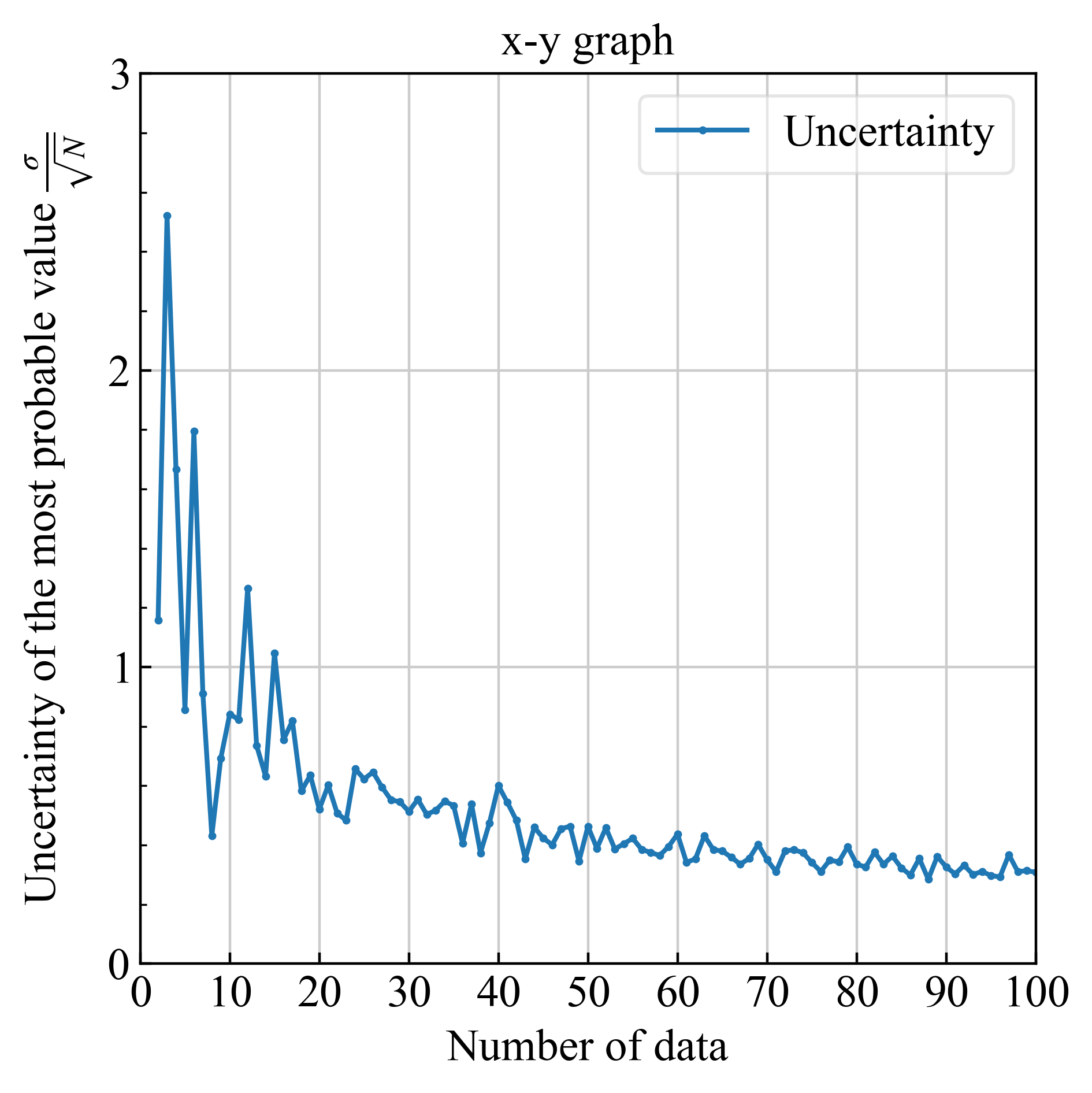正しい計算は青実線 (不偏標準偏差、式\eqref{eq20})	$\sigma/\sqrt{N}$, $\sigma$は式\eqref{eq20}.

3.2.2. 標準偏差との差 #

真値が分かっている場合の偏差（\eqref{eq19}の右辺）と$1/N$(間違い)または$1/(N-1)$(正しい、\eqref{eq20})で割って求めた偏差の差

	標準偏差と不偏標準偏差との差の比較
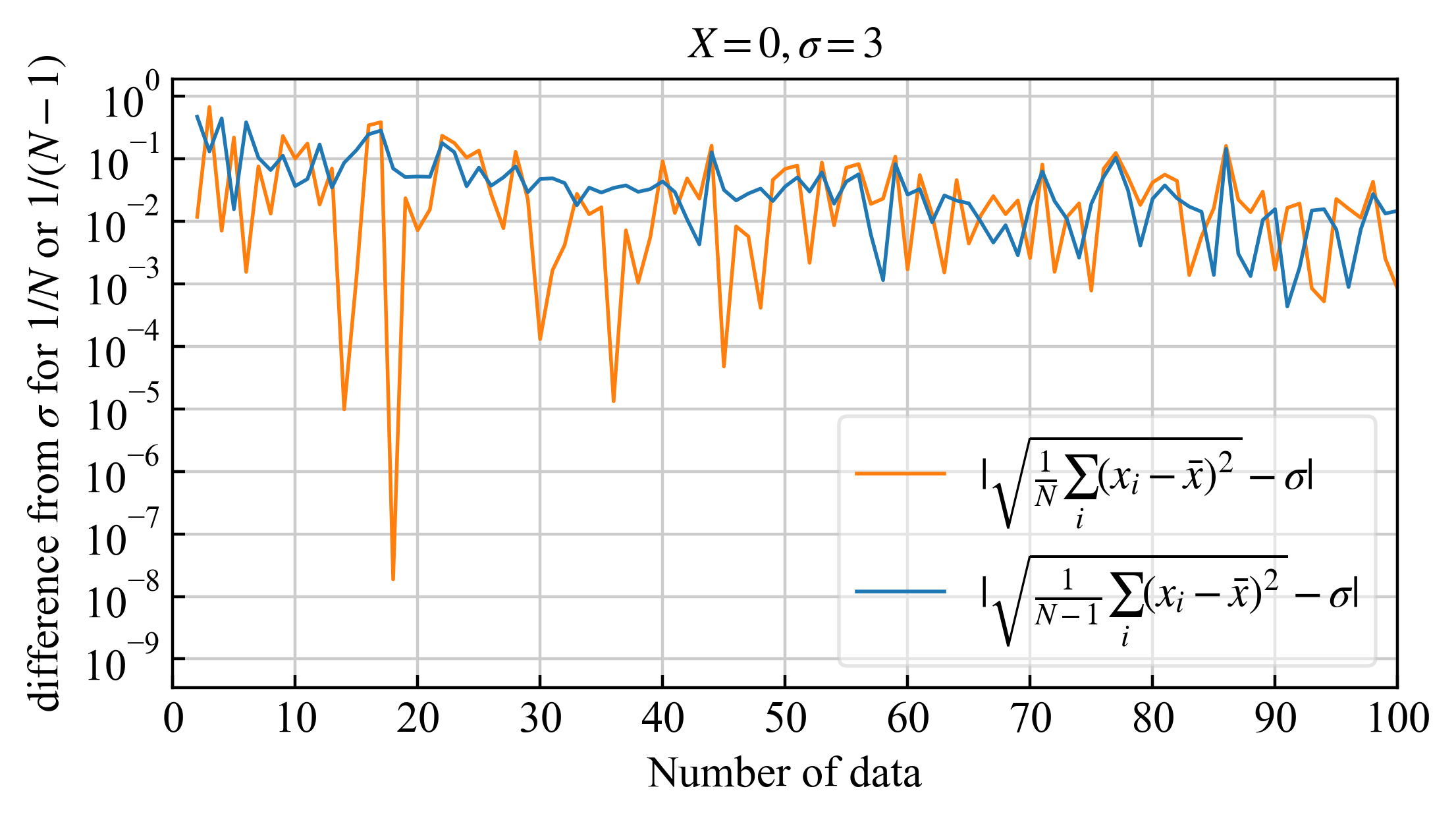	正しい計算は青実線 (|不偏標準偏差-標準偏差|)

差が大きい所に注目すると、正しい計算（青実践）の方が平均的に安定してオレンジより微妙に小さいです。ですが劇的ではないですね。

3.2.3. 最確値とエラーバー #

最確値に不確かさを含め、エラーバーと共に書くと下記のようになります。

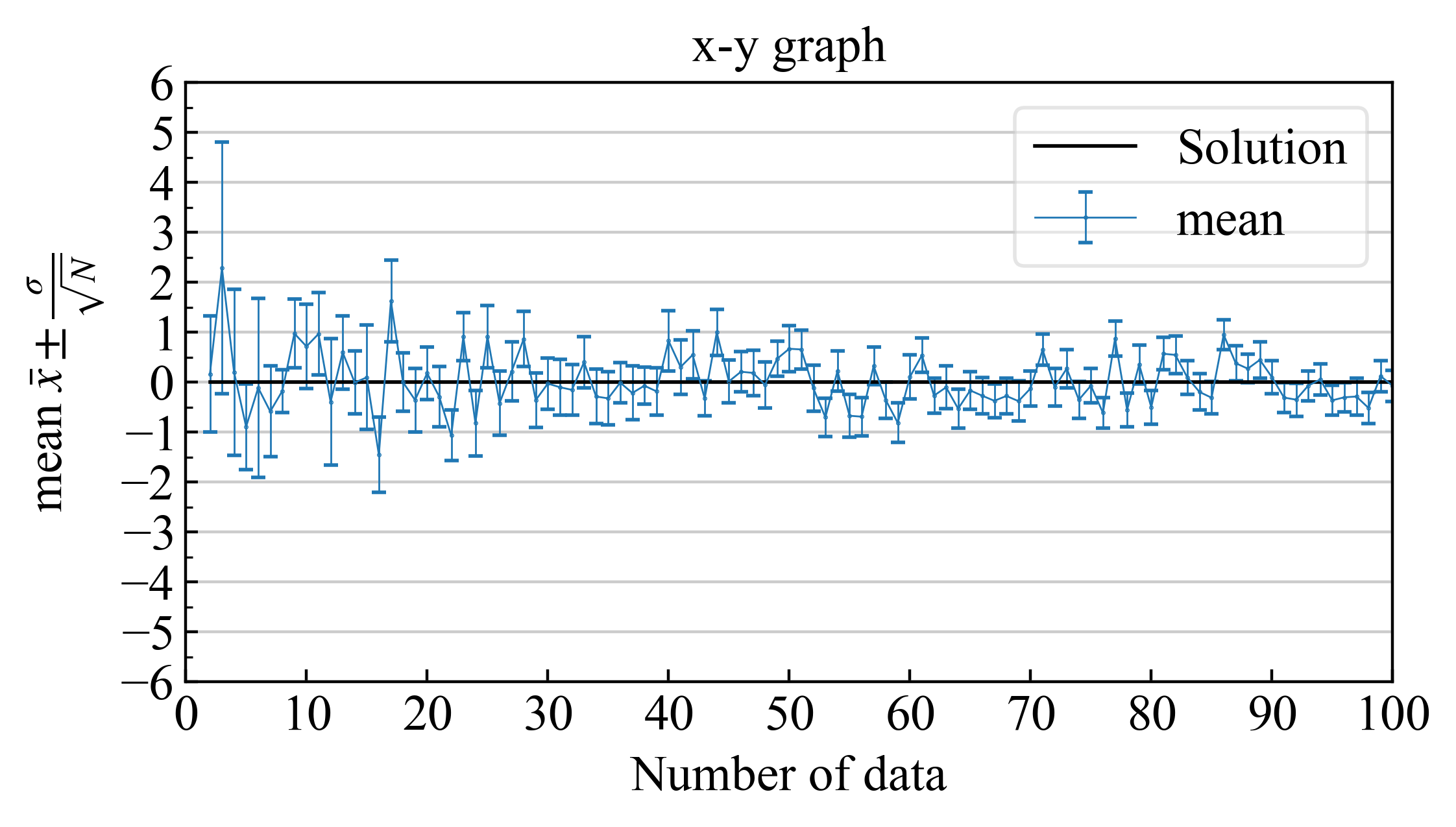	エラーバーの範囲に真値が入る確率が$68.3\%$

3.3. データ点数 $N\leq 100000$の場合（刻み幅100） #

3.3.1. 偏差・不確かさ #

偏差	不確かさ
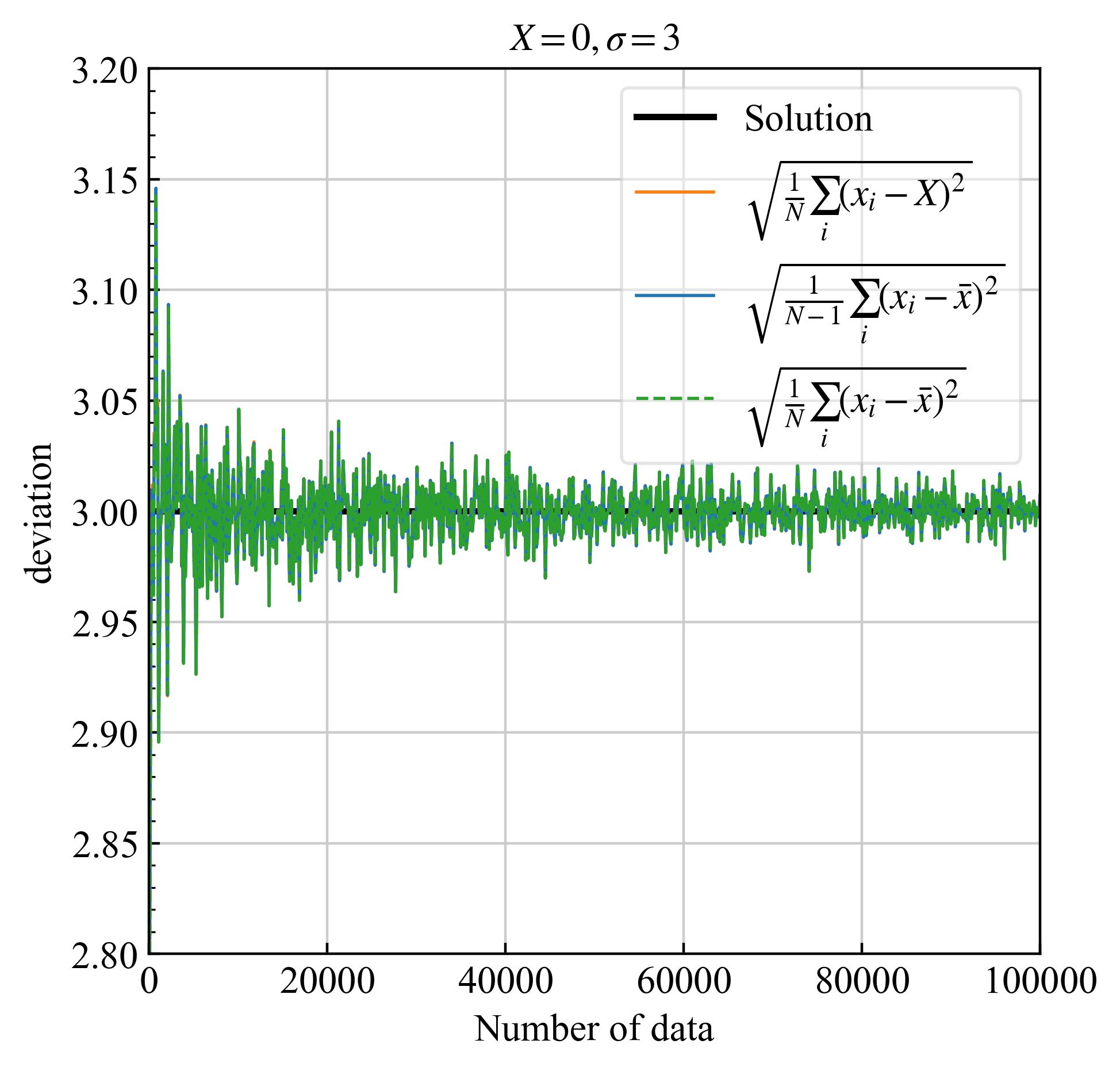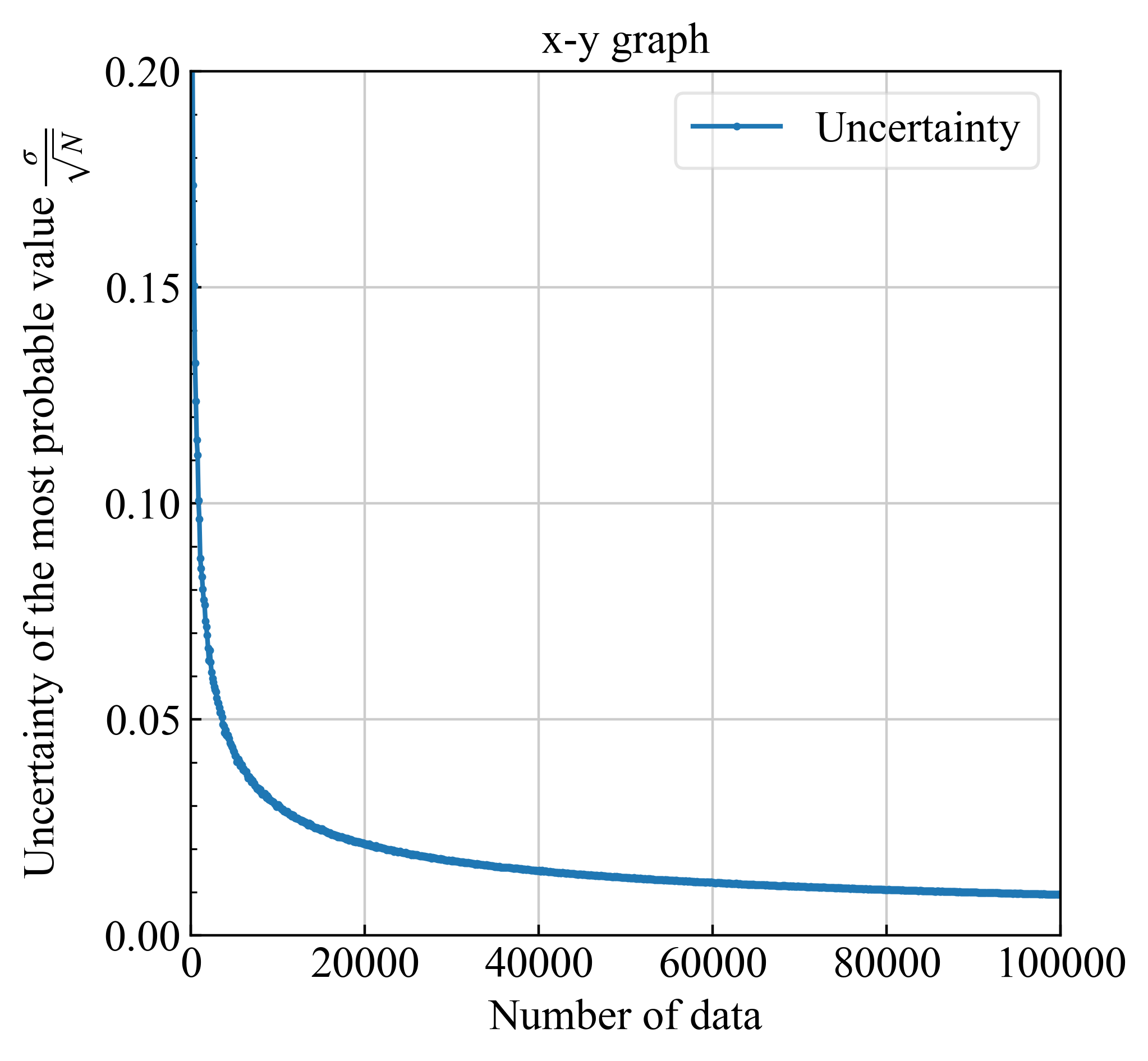正しい計算は青実線 (式\eqref{eq20})	$\sigma/\sqrt{N}$, $\sigma$は式\eqref{eq20}.
	不確かさを対数で表示
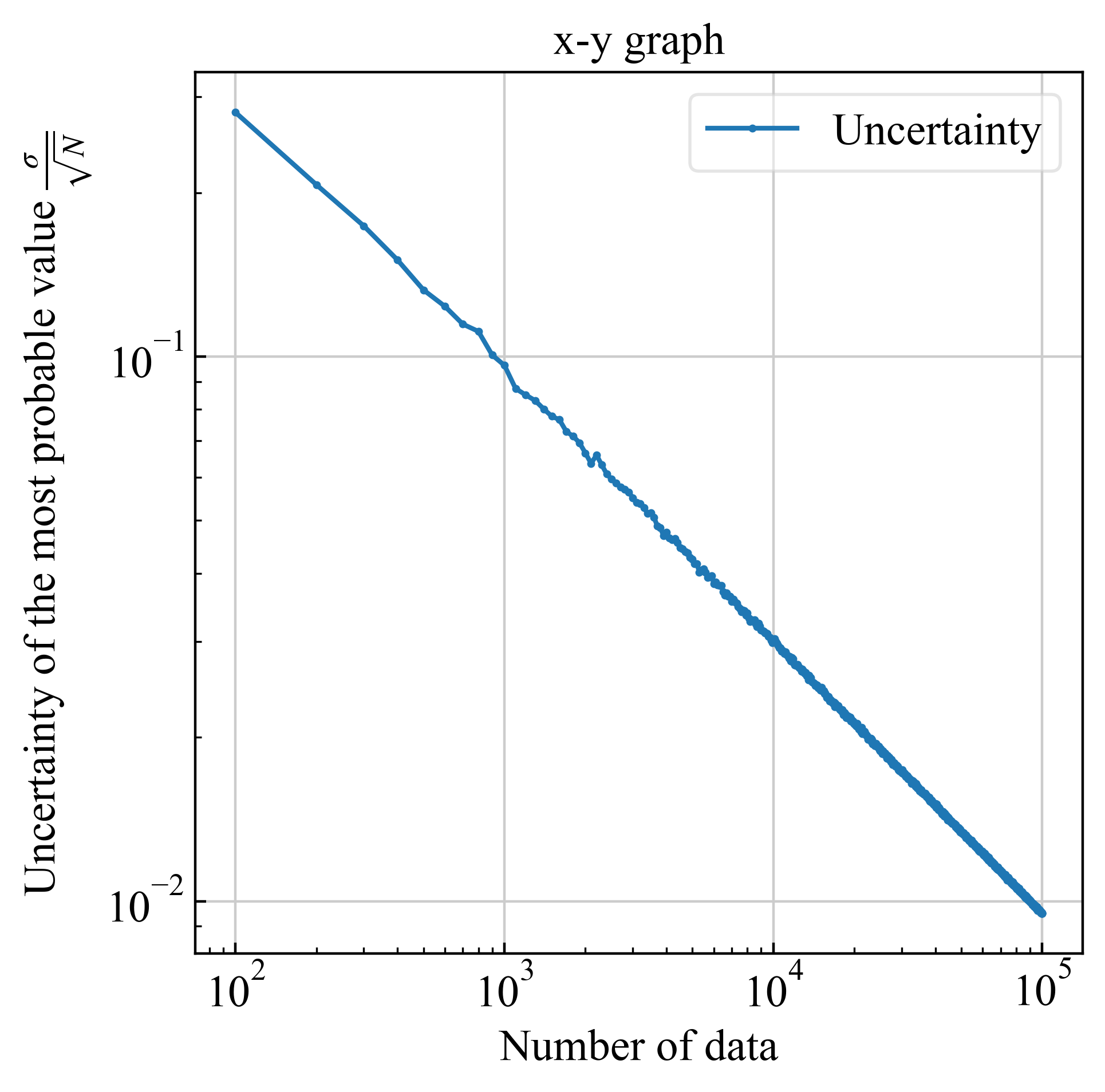	※$1/\sqrt{N}$によってデータ点数が100倍になると、不確かさが1桁小さくなる

3.3.2. 標準偏差との差 #

	標準偏差と不偏標準偏差との差の比較
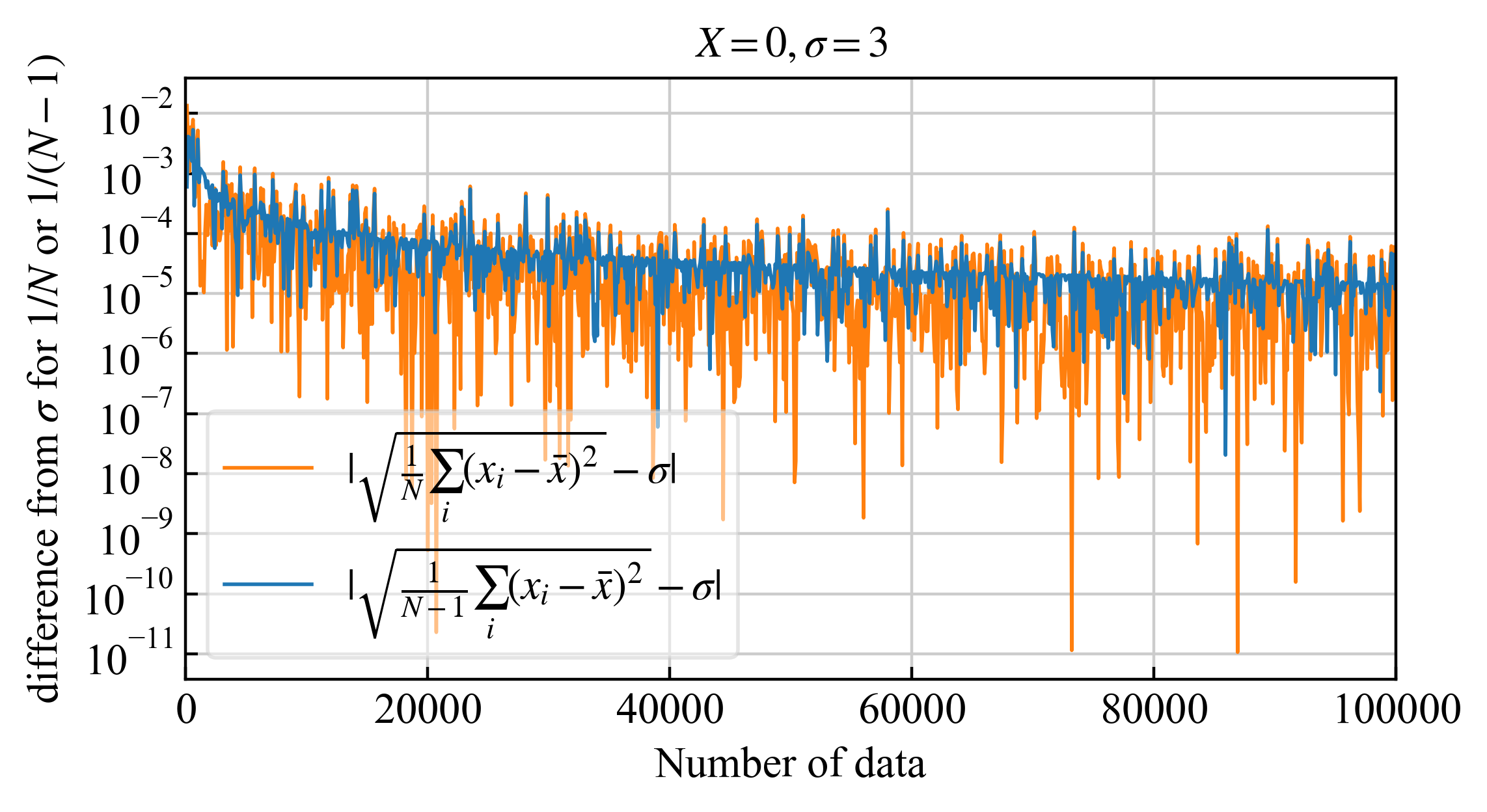	正しい計算は青実線 (|不偏標準偏差-標準偏差|)

3.3.3. 最確値とエラーバー #

最確値に不確かさを含め、エラーバーと共に書くと下記のようになります。

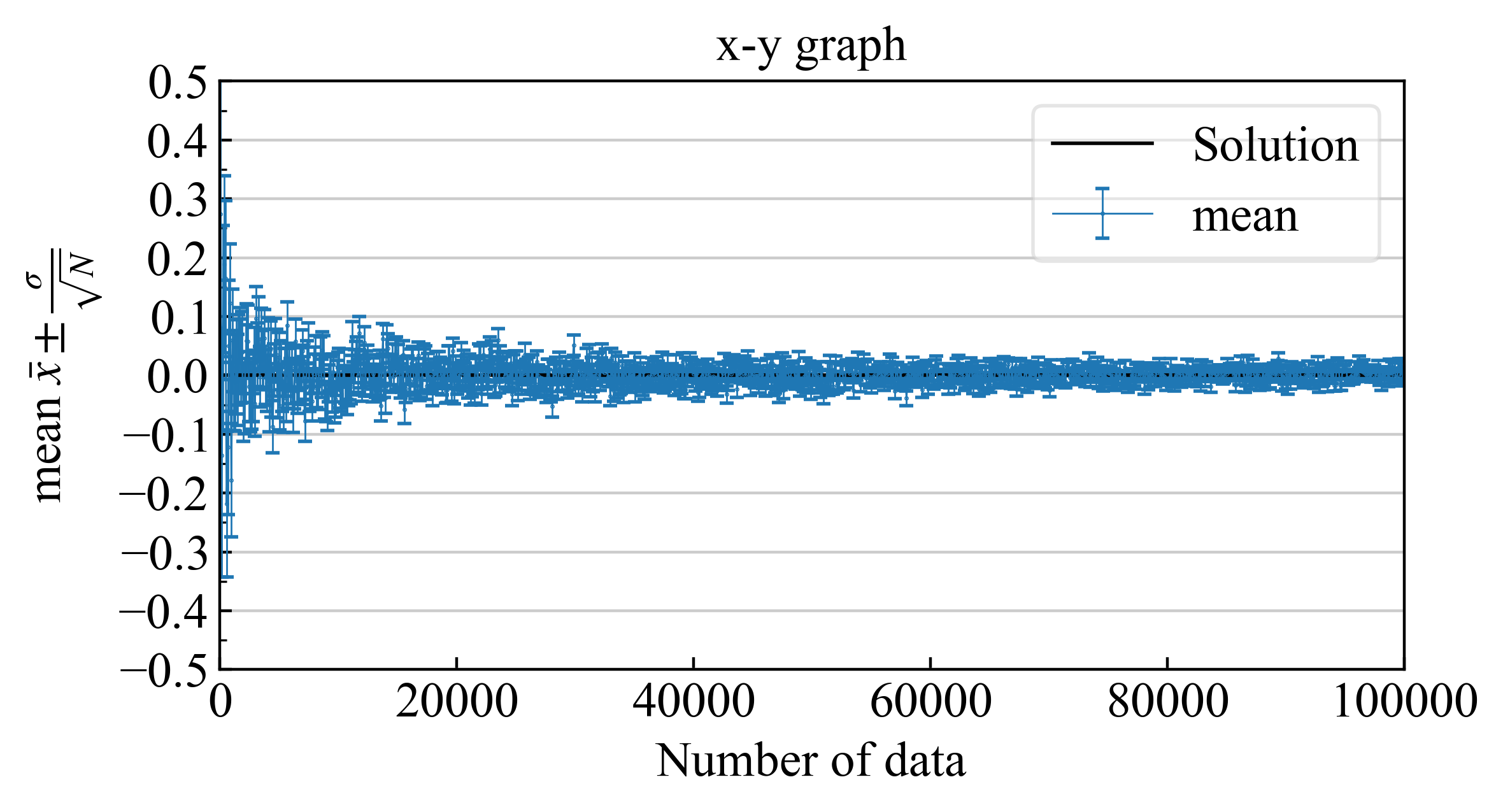	エラーバーの範囲に真値が入る確率が$68.3\%$

3.4. プログラム #

下記に、上記の図を作成した場合のpythonプログラムを置きます。

import numpy as np
from plot_xy import plot_xy
import matplotlib.pyplot as plt

# 平均値と分散を指定
mu = 0  # 平均値
sigma = 3  # 標準偏差

start = 2
step = 1
count = 998
N_points = [start + i * step for i in range(count)]

np.random.seed(5)

means = []  # \bar{x} = \frac{1}{N}\sum_{i=1}^{N}x_i
biased_deviations = []  # \sqrt{ \frac{1}{N} \sum_{i=1}^{N}(x_i-mu)^2 }
unbiased_deviations = []  # \sqrt{ \frac{1}{N-1} \sum_{i=1}^{N}(x_i-\bar{x})^2 }
uncertainties_of_mean = []  # \frac{1}{\sqrt{N}} \times \sqrt{ \frac{1}{N-1} \sum_{i=1}^{N}(x_i-\bar{x})^2 }
for N in N_points:
    # Generate N random numbers following a normal distribution with mean \mu and standard deviation \sigma.
    samples = np.random.normal(mu, sigma, N)

    # Calculate the mean and unbiased variance of the generated random numbers.
    sample_mean = np.mean(samples)  # Mean
    biased_deviation = np.sqrt(np.mean((samples - mu) ** 2))  # Biased deviation (using true value)
    unbiased_deviation = np.sqrt(np.var(samples, ddof=1))  # Unbiased deviation

    print(f"N:{N}, Sample : {sample_mean:.6f}, {unbiased_deviation:.6f}, {biased_deviation:.6f}")

    means.append(sample_mean)
    biased_deviations.append(biased_deviation)
    unbiased_deviations.append(unbiased_deviation)
    uncertainties_of_mean.append(unbiased_deviation / np.sqrt(N))

# -------------------------------------

# - Show histgram
count, bins, ignored = plt.hist(samples, bins=50, density=True)
# Calculate the center of bins
bin_centers = 0.5 * (bins[1:] + bins[:-1])
# Plot the line connecting the centers of the bins
plt.plot(bin_centers, count, "-")
plt.title("Histogram of Normally Distributed Numbers")
plt.xlabel("Points")
plt.ylabel("Frequency")
plt.legend()
plt.show()
plt.clf()

# - Show mean with error bar
plt.errorbar(N_points, means, yerr=uncertainties_of_mean, elinewidth=1, fmt=".-", ms=3, label="with error", capsize=2, capthick=1)
plt.xlabel("Points")
plt.ylabel("Most probable value")
plt.legend()
plt.show()
plt.clf()

# - Deviation
plt.plot(N_points, biased_deviations, ".-", ms=3, label="biased deviation")
plt.plot(N_points, unbiased_deviations, ".-", ms=3, label="unbiased deviation")
plt.xlabel("Points")
plt.ylabel("Deviation")
plt.legend()
plt.show()
plt.clf()