円周率の手計算 #
1. 導入 #
例えば知識だけを持って中世程度の異世界に転生した状況を考えます。
かの亜留間次郎さんは
まず自分が頭のいいところを偉い人に示して、それを認めて貰わないと進めない。
円周率を示し、凄いと思わせなさい。
(執筆者による意訳込み)と言われました1。
本稿では、実際に円周率をどうやって計算し、どうやって導出または証明すれば良いか?の一例を考えてみます。
もちろん、転生先ではアラビア数字や文字は異なるはずなので、転生先の数字・記号に変換することを忘れずに。
人類史における円周率の桁数の世界記録は下記の通りです2。
- 西暦1500年前は3~5桁 (多角形の利用)
- 西暦1500年頃で9桁 (多角形の利用)
- 西暦1600年頃で20~35桁 (多角形の利用)
- 西暦1700年頃で100桁 (atan系公式の利用)
我々が狙う転生先は西暦1700年程度の文明レベルです。 円周率の計算は、数日かければ20~30桁程度が得られるような方法を目指します。
これを目指す理由は、atanを使用する方法が発見される以前は多角形を用いる計算が主流で、その計算は年単位で計算が行われてようやく20桁、という事がザラだったためです3。 そのため、数日で20~30桁は確実に凄いと思わせられるでしょう。
西暦1700年以降に転生した場合でも、可能性は十分あります。 なぜなら、上記は後年判明した桁数であったり、秘匿されている可能性など様々あるからです。 また、情報が伝わる速度もそこまで早くないので、ある国で発見されたからと言って全世界に広がるわけではないのだろうと思います。
もっと円周率の歴史的な経緯を知りたい方は、『円周率πの手計算史』を参照してください4。
2. 転生先の設定 #
- コンピュータは存在しない
- 存在する世界線だったとしても、計算仮定を示すことが出来れば優秀な人材として認められるかもしれません。
- ある程度学問に理解がある世界
- 過去に遡りすぎてもダメです。しかしギリシャ等にピンポイントで転生すれば紀元前でもまだ可能性がありますが、円周率は無理数なのでこれを主張しすぎると○される可能性があります5。
- 転生先がスパルタだったらどうしようもないですね。逃げるか諦めるか、郷に従いましょう。
2.1. 準備 #
- 書くものと書かれるものを調達
- これが非常に難しいかもしれません。
- 石筆と石板、筆と和紙、羽ペンと羊皮紙などなど何でも良いです。
- 師を見つける/公開する場を見つける
- 折角導出しても、理解してもらえる環境ではないと取り越し苦労になります。
書くもの、書かれるものが無いまたは非常に高価である場合、製作するのも手です6。
3. 円周率について #
- 円周率は無理数である
- 円周率は超越数である
3.1. 手計算の工夫 #
- 計算量が少ない方法を選ぶ
- 計算機が無いので、大きな数同士の掛け算・割り算の計算コストが高いです。行うにしても大きな数と1,2桁の掛け算・割り算にしましょう。
- 割り算は極力避ける
- 割り算は非常に計算コストが高いです。小さい数で割るのは余り難しくないですが、大きい数で割るのは大変です。
4. 計算方法 #
ざっくりとこのように計算していきます。
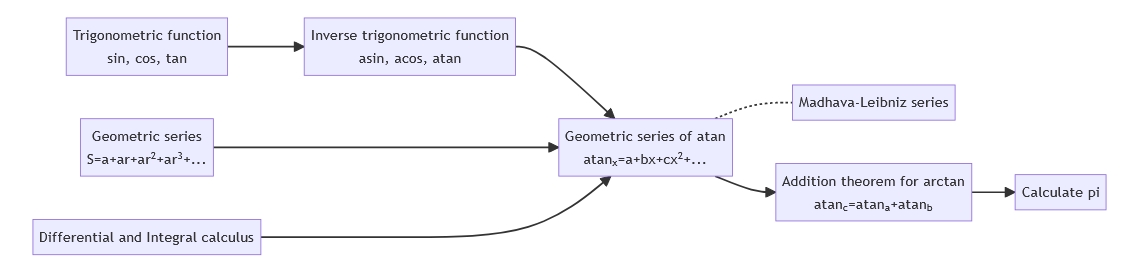
4.1. 三角関数・逆三角関数 #
恐らく、三角関数は知られているかと思います。 人類史でも紀元前1世紀くらいにはある程度知られていたそうです7。 ただし、江戸では角度の概念が無かったとのこともあり、現地の言葉に直して説明するのも難しいかもしれません8。
4.1.1. 三角関数 #
単位円を書いて説明して、ついでにピタゴラスの定理にも触れて説明しましょう。 ある程度不十分な説明でも、導出手順に追求されるのは
『こいつ、円周率を20桁まで求めやがったスゲーッ!!!!!』
となった後なので、多少意味不明な説明になっても大丈夫です。結果がそうなんだからそうなんだ!でごり押しましょう。
…余り問題にはならない事を期待します。
4.1.2. ラジアンの概念 #
ラジアン (radian) は、円周の長さと角度を結び付ける量で、導入しておくと便利です。 ざっくり説明するならば、
- 半径1の円を考える
- この時、円周は$2\pi$
- この円周を角度ラジアンとして採用する
ということです。 堅苦しくラジアンを定義すれば、
The radian is a unit of angular measure defined such that an angle of one radian subtended from the center of a unit circle produces an arc with arc length 1.
として定義されます9。日本語では、
円周上でその円の半径と同じ長さの弧を切り取る2本の半径が成す角の値
となります10。
ラジアンを定義しておくと、角度と円周率を直感的に結び付けることができます。 三角関数の導入が終わっているはずなので、ラジアンによって角度を測ることを採用すると
\begin{align}\label{tanpi4} \tan\left(\frac{\pi}{4}\right)=\frac{\sin\left(\pi/4\right)}{\cos\left(\pi/4\right)}=1 \end{align} を得ます。
4.1.3. 逆三角関数 #
逆三角関数の概念も、もし三角関数が知られている世界線であれば簡単かと思います。
『三角関数の値が分かっているときに、逆に角度を求める関数を逆関数と定義します。』
といえば何とかなるかと思います。 逆三角関数を使用すれば、式\eqref{tanpi4}より
\begin{align} \label{atanpi4} \frac{\pi}{4}=\text{atan}\left(1\right) \end{align}
となります。つまり、何とかして右辺の$\text{atan}$を計算しやすい形に持っていけば、それを4倍するだけでよいわけです。そこで登場するのが級数展開です。
4.2. $\text{atan}(x)$の級数展開 #
級数展開の歴史は古く、明示的に表れるのは西暦500年ころのインドのアーリヤバタ11によって発展した著書"Aryabhatiya"12で記述されたようです。 しかし、紀元前200年の頃でもアルキメデスやアポロニウスによって、級数の概念や基礎は使われていたようですので、若干受け入れられやすいでしょう。
この節で導出したい関係式は、$\text{atan}(x)$に対する級数展開で、下記の数式を導くのがゴールとなります13。
\begin{align}\label{atan1} \text{atan}(x) = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1}x^{2n+1},~~|x|< 1 \end{align}
では、式\eqref{atan1}を導出していきましょう。
最も簡単に$\text{atan}(x)$の級数展開を得るには、等比級数と微分・積分を使用します。 導出は、下記の順序で行います。
- $\text{atan}(x)$を微分すると、等比級数の形になる
- 等比級数の表記となった$\text{atan}(x)$の微分を積分する
- 級数の形で$\text{atan}(x)$を得る
4.2.1. 微分 #
人類史では、微分・積分は1600年代にアイザック・ニュートンとゴットフリート・ライプニッツによって発展してきました14。 微分・積分の説明は割愛しますが、関数の傾きと面積であることが説明できれば、とりあえずは良いでしょう。
まず、$\text{atan}(x)$の微分を考えると、 \begin{align} \label{dinvatan} \frac{d}{dx}\text{atan}(x)=\frac{1}{1+x^2} \end{align} が得られることを示します。これを示すには、逆関数の微分を利用します。
ざっくり逆関数の微分を説明すると、$y=f(x)$の逆関数が存在するならば、 \begin{align}\label{finv} \frac{dy}{dx}=\frac{1}{\hspace{0.5em}\frac{dx}{dy}\hspace{0.5em}} \end{align} が成立するというものです。
まず関数$y$を下記のように定義します。 \begin{align} y\equiv\text{atan}(x) \to x=\tan(y) \end{align}
両辺を$y$で微分して、 \begin{align} \frac{dx}{dy} &=\frac{d}{dy} \tan(y) =\frac{\cos^2{y}+\sin^2{y}}{\cos^2{y}} \nonumber \\ &=\frac{1}{\cos^2{y}} \nonumber \\ &=1+\tan^2(y) \nonumber \\ &=1+x^2 \end{align} となります。ここで、 \begin{align} 1+\tan^2{y}=\frac{1}{\cos^{2}(y)} \end{align} を使用しました。この式は、$\sin^2(x)+\cos^2(x)=1$の両辺を$\cos^2(x)$で割ることで得られます。
ここで、逆関数の微分\eqref{finv}を使用すれば、 \begin{align} \frac{d}{dx}\text{atan}(x)=\frac{1}{1+x^2} \end{align} であり、式\eqref{dinvatan}を得ます。
4.2.2. 等比級数・積分 #
式\eqref{dinvatan}の右辺$\frac{1}{1+x^2}$は、等比級数の形によく似ています。
等比級数である等比数列の総和は、初項$1$, 公比$|r|<1$の場合に \begin{align}\label{geometric} \frac{1}{1-r}=1+r+r^2+r^3+\cdots \end{align} という関係が成立します。導出するためには、等比数列とそれに$r$を掛けた等比数列の差を求めれば導けます。
等比級数\eqref{geometric}に対し、$r=-x^2,~|x|<1$を採用してみます。 \begin{align} \frac{1}{1+x^2}=1-x^2+x^4-x^6+\cdots \end{align} 左辺は、式\eqref{dinvatan}で求めた$\text{atan}(x)$の微分に等しいので、 \begin{align} \frac{d}{dx}\text{atan}(x)=1-x^2+x^4-x^6+\cdots \end{align} となります。両辺を区間$[0,s]$の範囲で$x$について積分すれば、 \begin{gather} \int_{0}^s dx \left[\frac{d}{dx}\text{atan}(x)\right] = \int_{0}^s dx \left(1-x^2+x^4-x^6+\cdots\right) \nonumber \\ \text{atan}(s)-\text{atan}(0) = \left[x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots\right]_{0}^{s} \nonumber \\ \text{atan}(s)=s-\frac{1}{3}s^3+\frac{1}{5}s^5-\frac{1}{7}s^7+\cdots,~ |s|<1 \end{gather}
となります。最後の式変形で$s$を改めて$x$と置けば、$\text{atan}(x)$の級数展開を得ます。 \begin{align} \text{atan}(x)&=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots \nonumber \\ &=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{2n+1}x^{2n+1},~ |x|<1 \label{atantaylor} \end{align}
式\eqref{atantaylor}の右辺を見て分かりますが、$x$が小さいほど、項数が増えるに連れて新たに足す数が急速に小さくなります。
また、級数展開\eqref{atantaylor}は$\text{atan}(x)$の点$x=0$周りのテイラー展開となっています。 もし、テイラー展開の方が発展していたら、この級数展開と絡めて説明しても良いと思います。
4.2.3. マーダヴァ-ライプニッツ級数 #
さて$x=1$の場合、級数展開\eqref{atantaylor}の式は使用できないという結論になりますが、アーベルの連続性定理15より$x=1$でも使用できることが分かっています。
実際の計算を行う場合、もう一段階工夫をするので$x=1$の問題は回避するので、議論をしなくても良いです。
ただし、$x=1$の場合はマーダヴァ-ライプニッツ級数 (Madhava–Leibniz series) として知られており、単純な級数と円周率を結び付ける素敵な下記の式になります。
\begin{align}\label{ML} \frac{\pi}{4}=\text{atan}(1)&=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots \\ \end{align}
4.3. $\text{atan}$系公式の作成 #
さて、もし$x=1$で級数展開が使用できるならば、
\begin{align} \frac{\pi}{4}&=\text{atan}\left(1\right)\nonumber \\ &=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots \label{pi_ML} \end{align}
より、右辺を適当な項数で打ち切ることによって$\pi$の近似値を得ることができます。 しかし、例えば\eqref{pi_ML}の右辺を500項まで計算しても右辺501項目は$\frac{1}{1003}\approx 0.001$であり、小数点第2位程度まで影響を与えてしまいます。つまり、500項計算しても$\pi\approx 3.1$程度しか求めたことにならず、使い物になりません。
そこで、$\text{atan}\left(1\right)$を何とかして引数が1より小さい数の和で書くようにします。
4.3.1. $\text{atan}$の加法定理 #
$\text{atan}$には、下記の加法定理が存在します。
\begin{align} \text{atan}(a)+\text{atan}(b)=\text{atan}\left(\frac{a+b}{1-ab}\right) \end{align}
もし右辺の引数が$1$で、$a, b < 1$であるような組み合わせがあれば級数の収束が早くなり、計算量を大幅に減らせます。
まずはこの加法定理を導出してみましょう。
三角関数の加法定理より \begin{align} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \label{sinadd}\\ \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta \label{cosadd}\\ \end{align}
が得られます16。式\eqref{sinadd}を式\eqref{cosadd}で割ると、
\begin{align} \tan(\alpha+\beta)&=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \nonumber \\ &=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta} \end{align} です。両辺の分子分母に$1/(\cos\alpha\cos\beta)$を掛ければ、$\tan$の加法定理 \begin{align}\label{tanadd} \tan(\alpha+\beta)&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \end{align} を得ます。
\eqref{tanadd}の逆関数を考えると \begin{align} \alpha+\beta=\text{atan}\left[\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\right] \end{align} となるので、$a=\tan\alpha, b=\tan\beta$を新たに導入すると$\text{atan}$の加法定理 \begin{align} \text{atan}(a)+\text{atan}(b)=\text{atan}\left(\frac{a+b}{1-ab}\right) \label{atanadd} \end{align} を得ます。
4.3.2. $\text{atan}(1)$の分割 #
仮に\eqref{atanadd}の右辺の引数が$1$である時、どのように分割されるでしょうか?この問題は \begin{gather} \frac{a+b}{1-ab}=1 \end{gather} であるような$a, b < 1$を探すという問題です。$a, b$は実数です。 最終的な関係式が重要なので当てずっぽうに探しても良いですが、効率的に計算しやすい数による加法定理を見つけるために少し工夫をしましょう。
下記の形で、加法定理を探すことにします。
\begin{gather} \text{atan}\left(\frac{1}{l}\right)=\text{atan}\left(\frac{1}{n}\right)+\text{atan}\left(\frac{1}{m}\right) \end{gather}
ここで、$l, m, n$は整数で、$l < m, n$の関係があるとします。つまり、 \begin{gather} \frac{a+b}{1-ab}=\frac{1}{l},\hspace{1em}a=\frac{1}{m},\hspace{1em}b=\frac{1}{n} \end{gather} となるような整数$l, m, n$を探す問題に変えます。$a, b$を消去し、$n$を求める式に変形すると、 \begin{gather} n=\frac{1+ml}{m-l} \end{gather} を得ます。右辺の分母の形より、組み合わせの一つとして$m=l+1$に選べばいつも$n$が整数になることが分かります。
例えば、$l=1$ならば、解の組み合わせを$(l, m, n)$と表現して、$l, m, n (l < m, n)$を求めると \begin{gather} n=\frac{1+m}{m-1} \hspace{1em}\to\hspace{1em} (l, m, n)=(1, 2, 3) \end{gather} が見つかります。つまり、$\text{atan}$の加法定理として、 \begin{gather} \text{atan}\left(1\right)=\text{atan}\left(\frac{1}{2}\right)+\text{atan}\left(\frac{1}{3}\right) \end{gather} を得ます。
更に右辺に現れる$k=2, k=3$について加法定理を適用していけば、近似計算の収束を早める大きな助けとなります。
この先、手計算で行うことを考えて10進数で出来るだけ割り算が行いやすい$m=2, 5$で表されることを期待し、色々と調べてみます。 すると一例ですが下記の加法定理を見つけることができます。
| $(l, m, n)$ | $\text{atan}$の加法定理 |
|---|---|
| $(1, 2, 3)$ | $\text{atan}(1)=\text{atan}(1/2)+\text{atan}(1/3)$ |
| $(2, 3, 7)$ | $\text{atan}(1/2)=\text{atan}(1/3)+\text{atan}(1/7)$ |
| $(3, 5, 8)$ | $\text{atan}(1/3)=\text{atan}(1/5)+\text{atan}(1/8)$ |
| $(7, 8, 57)$ | $\text{atan}(1/7)=\text{atan}(1/8)+\text{atan}(1/57)$ |
以上より、$\text{atan}(1)$が手計算しやすそうな展開として下記の公式が見つかります。 \begin{align} \text{atan}(1)&=2~\text{atan}(1/5)+3~\text{atan}(1/8)+\text{atan}(1/57) \label{atanmy}\\ \text{atan}(1)&=2~\text{atan}(1/5)+\text{atan}(1/7)+2~\text{atan}(1/8)\label{atanmysub} \end{align}
4.4. 具体的な計算 #
これまでの議論により、関係式\eqref{atanmy}と\eqref{atanmysub}を得ましたが、式\eqref{atanmy}を元に考えていきます。つまり \begin{align} \frac{\pi}{4}=2~\text{atan}(1/5)+3~\text{atan}(1/8)+\text{atan}(1/57) \end{align} を考えていきます。両辺に4を掛けて$\pi=$の形にすれば、 \begin{align} \pi=8~\text{atan}(1/5)+12~\text{atan}(1/8)+4~\text{atan}(1/57) \end{align} を得ます。
近似値は右辺の$\text{atan}$の級数展開を有限項まで計算することで得られます。つまり \begin{align}\label{pitaylor} \pi\approx 8\sum_{i=0}^{N_i}\frac{(-1)^i}{2i+1}\frac{1}{5^{2i+1}}+12\sum_{j=0}^{N_j}\frac{(-1)^j}{2j+1}\frac{1}{8^{2j+1}}+4\sum_{k=0}^{N_k}\frac{(-1)^k}{2k+1}\frac{1}{57^{2k+1}} \end{align} です。後は右辺の$N, M$を十分大きくしていけばいくらでも$\pi$に近づきますので、満足するまで計算すれば良いです。
具体的に計算するには数表をまず作成するのが良いでしょう。 その後、係数を掛けたり引いたりして、円周率を求めます。
今は実際に転生したわけではないので、円周率10桁を目標に実際に求めてみましょう。
以降は、単なる泥臭い計算ですので、下記は知っておかなくても時間を掛ければ何とかなる項目です。
4.4.1. 数表の作成 #
まずは単純な計算をあらかじめ実施します。今回は、10桁程度求めることを目標にするので、0が10個程度並ぶまで作成して計算しておきます。
| $n$ | $(1/5)^{n}$ | $(1/7)^{n}$ | $(1/8)^{n} = (1/2)^{3n}$ | $(1/57)^{n}$ |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0.2 | 0.142 857 142 857 | 0.125 | 0.017 543 859 649 |
| 2 | 0.04 | 0.020 408 163 265 | 0.015 625 | 0.000 307 787 011 |
| 3 | 0.008 | 0.002 915 451 895 | 0.001 953 125 | 0.000 005 399 772 |
| 4 | 0.001 6 | 0.000 416 493 128 | 0.000 244 140 625 | 0.000 000 094 733 |
| 5 | 0.000 32 | 0.000 059 499 018 | 0.000 030 517 578 | 0.000 000 001 662 |
| 6 | 0.000 064 | 0.000 008 499 860 | 0.000 003 814 697 | 0.000 000 000 029 |
| 7 | 0.000 012 8 | 0.000 001 214 266 | 0.000 000 476 837 | 0.000 000 000 001 |
| 8 | 0.000 002 56 | 0.000 000 173 467 | 0.000 000 059 605 | |
| 9 | 0.000 000 512 | 0.000 000 024 781 | 0.000 000 007 451 | |
| 10 | 0.000 000 102 4 | 0.000 000 003 540 | 0.000 000 000 931 | |
| 11 | 0.000 000 020 48 | 0.000 000 000 506 | 0.000 000 000 116 | |
| 12 | 0.000 000 004 096 | 0.000 000 000 072 | ||
| 13 | 0.000 000 000 819 | 0.000 000 000 010 | ||
| 14 | 0.000 000 000 164 | |||
| 15 | 0.000 000 000 033 |
数表を作成するうえで、割り算はミスが出るかもしれません。そのため適当な倍数を掛けた場合に簡単になるならばそれを採用するのも良いです。つまり、 \begin{align} \frac{1}{8} = \frac{125}{1000} \end{align} なので、8で割ることは125を掛けて小数点の位置を3つずらす操作と同じ、と考えて計算を進めても良いです。
$1/57=(1/3)\cdot(1/19)$とできますが、素直に計算した方が良いと思います。 もしくは、使う公式を\eqref{atanmysub}に変えても良いでしょう。こちらは1桁の割り算しか出てこないです。
4.4.2. $\text{atan}(1/n)$の近似値 #
級数展開に含まれるそれぞれの項の符号を除いて、各項を計算すると下記表の通りになります。
下記の表は、 \begin{gather} \label{an} \text{atan}(x) = \sum_{n=0}^{\infty} (-1)^{n}a_n,\hspace{2em} a_n = \frac{1}{2n+1}\left(\frac{1}{x}\right)^{2n+1} \end{gather} と$a_n$を定義した場合の$a_n$の値です。先に作成した数表を元に、$a_n$を計算します。
| $n$ | $\frac{1}{2n+1}(\frac{1}{5})^{2n+1}$ | $\frac{1}{2n+1}(\frac{1}{7})^{2n+1}$ | $\frac{1}{2n+1}(\frac{1}{8})^{-(2n+1)}$ | $\frac{1}{2n+1}(\frac{1}{57})^{-(2n+1)}$ |
|---|---|---|---|---|
| 0 | 0.200 000 000 000 | 0.142 857 142 857 | 0.125 000 000 000 | 0.017 543 859 649 |
| 1 | 0.002 666 666 667 | 0.000 971 817 298 | 0.000 651 041 667 | 0.000 001 799 924 |
| 2 | 0.000 064 000 000 | 0.000 011 899 804 | 0.000 006 103 516 | 0.000 000 000 332 |
| 3 | 0.000 001 828 571 | 0.000 000 173 467 | 0.000 000 068 120 | |
| 4 | 0.000 000 056 889 | 0.000 000 002 753 | 0.000 000 000 828 | |
| 5 | 0.000 000 001 862 | 0.000 000 000 046 | 0.000 000 000 011 | |
| 6 | 0.000 000 000 063 | 0.000 000 000 001 | ||
| 7 | 0.000 000 000 002 |
これらの結果を\eqref{an}に代入し、下記の近似値を得ます。
\begin{align} \text{atan}(1/5) &\approx 0.197~395~559~852 \\ \text{atan}(1/7) &\approx 0.141~897~054~604 \\ \text{atan}(1/8) &\approx 0.124~354~994~546 \\ \text{atan}(1/57) &\approx 0.017~542~060~057 \end{align}
4.4.3. $\pi$の近似値と比較 #
最後に、\eqref{pitaylor}に従ってそれぞれを足します。すると、
\begin{align} \pi &= 8~\text{atan}(1/5)+12~\text{atan}(1/8)+4~\text{atan}(1/57) &\approx \underline{3.141~592~653~5}80 \end{align}
又は、
\begin{align} \pi &= 8~\text{atan}(1/5)+4~\text{atan}(1/7)+8~\text{atan}(1/8) &\approx \underline{3.141~592~653~5}84 \end{align}
を得ます。本当の答えは、
\begin{align} \pi = \underline{3.141~592~653~5}89 … \end{align}
ですので、目標とした10桁まで合っています。8もあっていますが、四捨五入した場合に真値と異なるので含めていません。 念のためですが、通常は10桁まで合わせたい場合、11~12桁程度まで計算して最後の桁を捨てます。
実際、私も数表の作成から手計算で頑張ってみましたが、10桁得るのに半日掛かりました。 計算ミスなどしょっちゅうでストレスも溜まります。計算機の偉大さが分かります。
4.5. 発展 #
級数展開は$x=0$におけるテイラー展開であり、その性質上$\text{atan}$の引数の値がゼロに近いほど正確になります。 計算のしやすさを考えた場合、良く知られるマチンの公式17が良いでしょう。
マチンの公式は下記のものです。
\begin{align} \frac{\pi}{4}=4~\text{atan}(1/5)-\text{atan}(1/239) \end{align}
級数展開をした場合、5の割り算は非常に簡単です。また、他の項も$239$とかなり大きい値なので、1項の計算は重いですが、そこまで計算する必要がありません。
もし詳細を知りたい方は、連鎖探索法18や、逆三角関数のテイラー展開を用いる方法19を参照するとよいでしょう。
5. まとめ #
皆様、これにて講座"異世界転生入門"は終了です。
これから運よく学問に明るい異世界に転生しましたら、ぜひ円周率と共に次のセリフを言いましょう。
あれ、俺何かやっちゃいました?
では、新たな人生をお楽しみください。
6. 変更履歴 #
2023/07/24: (4章の記号を$(l,n,m) \to (l,m,n)$に変更)
2023/07/22: 公開
7. Appendix #
$ab=n^2+1$を満たす整数$n$を選ぶとき、atanの加法定理は下記のように書き変えられます18。 \begin{align} \text{atan}\left(\frac{1}{n}\right)=\text{atan}\left(\frac{1}{n+a}\right)+\text{atan}\left(\frac{1}{n+b}\right) \end{align}
