クーロンポテンシャルによる散乱 #

1. 概要 #

電荷$q_A$を持つ原子核に、遠方から$q_B$を持つ電子が衝突する過程を考えます。 例えば、水素原子の原子核である陽子1個($q_B=+e$, eは電気素量)に対し、遠方から電子($q_A=-e$)が衝突する過程です。 相対座標に対する時間依存しないシュレーディンガー方程式は、 \begin{align} \label{tise0} \left[ -\frac{\hbar^2}{2\mu}\nabla^2+\frac{q_Aq_B}{4\pi\varepsilon_0 r} \right]\psi_c(\mathbf{r})=E\psi_c(\mathbf{r}) \end{align} と書くことができます。ここで、$\hbar$はプランク定数、$\varepsilon_0$は真空の誘電率、$\mu$はAとBの換算質量を表し, $E$は衝突のエネルギーを表します。 簡単にするために係数をまとめて \begin{align} \left[ \nabla^2-\frac{U_0}{r}+k^2\right]\psi_c(\mathbf{r})=0 \end{align} と書きます。ここで、 \begin{align} U_0\equiv \frac{2\mu}{\hbar^2}\frac{q_Aq_B}{4\pi\varepsilon_0},~~ k\equiv \sqrt{\frac{2\mu E}{\hbar^2}} \end{align} という量を定義しました。 これから、運動量$k$で定義される平面波が入射したらどのように応答するか？を知りたいので、式\eqref{tise0}を境界条件 \begin{align} \label{bc0} \psi_c(\mathbf{r})|_{z\to -\infty}=e^{ikz} \end{align} の下で解いていきます。

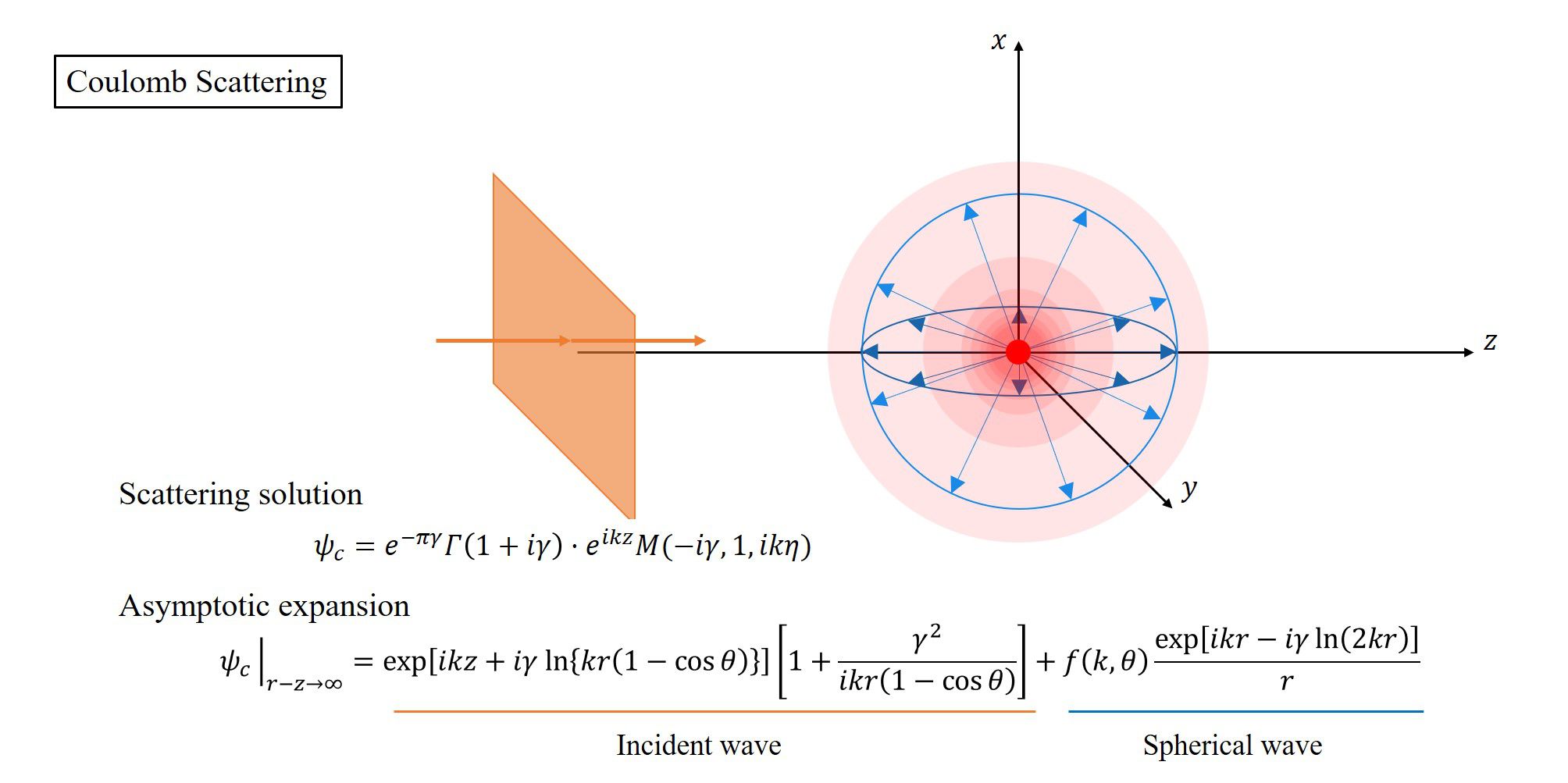
導出した結果は、 \begin{align} &\psi_c(\mathbf{r})\Bigr|_{|r-z|\to\infty} \nonumber\\ &=\exp{\biggl(ikz-i\gamma \ln\Bigl[kr(1-\cos\theta)\Bigr]\biggr)} \cdot\left(1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right) \nonumber\\ &\hspace{13em}+f(k,\theta)\frac{\exp \Bigl[ikr -i\gamma \ln(2kr)\Bigr] }{r} \label{asymcoulomb} \end{align} となります。この展開は$|r-z|\to 0$となる$z$軸上もしくはz軸近傍では使えないことを注記しておきます。元々の境界条件\eqref{bc0}は、$z\to -\infty$だけで決まっており$x,y$に条件はありませんが、$(x,y,z)$の座標系で見た場合に結論として得られるものは$z$軸からは離れた領域でなければならない、となります。正確には放物座標系で見たときの$\eta=r-z$の成分だけに条件が加わります。

ここで \begin{align} \gamma=\frac{U_0}{2k}=\frac{q_Aq_B}{4\pi\varepsilon_0}\frac{1}{\hbar\nu}=\frac{q_Aq_B}{4\pi\varepsilon_0}\frac{\mu}{\hbar^2 k} \end{align} であり、$\gamma$はSommerfeld parameterと呼ばれる量であり、$\nu=\frac{\hbar k}{\mu}$は２粒子間の相対速度を表しています。また、 \begin{align} f(k,\theta)=-\frac{\gamma}{2k\sin^2\frac{\theta}{2}} \cdot\exp\left[-i\gamma\ln\left(\sin^2\frac{\theta}{2}\right)\right] \cdot\frac{\Gamma(1+i\gamma)}{\Gamma(1-i\gamma)} \end{align} はクーロン散乱振幅と呼ばれる量であり、波数$k$を持って入射した平面波が、入射方向に対して角度$\theta$方向にどれだけ球面波が歪むか？を表す量です。 また、$\Gamma(x)$はガンマ関数であり、 \begin{align} \frac{\Gamma(1+i\gamma)}{\Gamma(1-i\gamma)}=\exp(2i\sigma_0) \end{align} と書かれる場合があります。$\sigma_0\equiv\arg(\Gamma(1+i\gamma))$は位相差と呼ばれます。

式\eqref{asymcoulomb}の右辺第一項は入射波、第二項は外向きの球面波を表します。指数関数の中にある$\ln$を含む項は対数の発散で、平面波$e^{ikz}$の形を妨げていることが分かります。これは、クーロンポテンシャルが長距離ポテンシャルであることに由来し、どんなに遠くであっても散乱の影響を受けることを意味します。別の言い方をすれば、クーロンポテンシャルの散乱半径が無限大だということを表しています。

本内容は、主にB. H. BransdenとC. J. Joachainによる著書 Physics of Atoms and Molecules (2nd Edition) の第12章5項 “The Coulomb potential” に基づきます¹。

Physics of Atoms and Molecules

B. H. Bransden and C. J. Joachain, Benjamin Cummings

Amazon

2. 散乱問題 #

時間依存しないシュレーディンガー方程式を変形した \begin{align} \label{tise} \left[ \nabla^2-\frac{U_0}{r}+k^2\right]\psi_c(\mathbf{r})=0 \end{align} を、境界条件 \begin{align} \label{bc} \psi_c(\mathbf{r})|_{z\to -\infty}=e^{ikz} \end{align} の下で解いていきます¹³。この境界条件の想定は、波数$k$を持つ平面波が$z\to-\infty$から入射し、原点に存在する原子核により散乱が起こり、外向きの球面波となる過程を想定しています。

2.1. 入射波として平面波を考える理由 #

なぜ平面波で入射する解を考えるのでしょうか？

この問いに対する答えの一つは、フーリエ変換です。
例えば実験で用意できる波束は、必ず有限の範囲の波束となります。そのため理想的な平面波は存在せず、近似的に平面波として扱うか有限範囲の波束のまま扱わなければなりません。 前者の場合は平面波の議論そのままで問題ありませんが、後者の場合は平面波で表すことはできません。 そこでフーリエ変換が登場します。 任意の初期状態が用意された時、平面波の重ね合わせとして表現できるというのがフーリエ変換なので、平面波に対する応答が分かれば任意の初期状態に対する応答が分かる、という狙いがあります。

これが平面波で入射する解を考える理由の一つです。

3. 散乱状態 #

さて、原子のようなクーロンポテンシャルの問題は、球面座標系や放物座標系などで変数分離を行うことが可能です。 現在考えたい問題は、平面波がクーロンポテンシャルによってどのように散乱されるかを考える問題です。 平面波という特定の方向が存在する問題は、球面的な状態と特定の直線的な方向が存在します。その場合、放物座標系を用いて変数分離していくのが便利です。

3.1. 放物座標系 #

放物座標系は、 \begin{align} \left\{ \begin{array}{l} \xi= r+z,\hspace{4em} (0\leq \xi < \infty)\\ \eta=r-z,\hspace{4em} (0\leq \eta < \infty)\\ \phi=\tan^{-1}\left(\frac{y}{x}\right),\hspace{1.5em} (0\leq \phi < 2\pi)\ \end{array} \right. \end{align} で表現される座標系です⁴²。放物座標系において、ラプラシアンは下記の通り導かれます。 \begin{align} \label{e3} \nabla^2=\frac{4}{\xi+\eta}\left(\frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}\right) +\frac{1}{\xi\eta}\frac{\partial^2}{\partial \phi^2} \end{align}

3.2. $\phi$方向の解 #

まず放物座標系におけるラプラシアンを見ると、$\phi$方向だけ解けてしまいそうなことに気が付きます。 そのため、散乱解が変数分離できると仮定します。つまり、 \begin{align} \psi_c(\mathbf{r})=\psi_c(\xi, \eta)\psi(\phi) \end{align} を考えます。

具体的な手順は省略しますが、$\psi(\phi)$について\eqref{tise}に代入し解けば、 \begin{align} \psi(\phi)\propto e^{im\phi} \end{align} と書けます。

今、入射平面波と球対称のポテンシャルの問題を考えているため、そこから得られる散乱解に$\phi$に対する依存性は無いだろうと予想できます⁵。 つまり$m=0$であることが分かります。よって$m=0$を採用して \begin{align} \label{psicr} \psi_c(\mathbf{r})=\psi_c(\xi, \eta) \end{align} となります⁶¹。

3.3. $\xi, \eta$方向の解 #

では残りの座標である$\xi, \eta$について方程式を考えていきましょう。
時間依存しないシュレーディンガー方程式\eqref{tise}に放物座標系のラプラシアン\eqref{e3}を代入すると \begin{gather} \left[\nabla^2-\frac{U_0}{r}+k^2\right]\psi_c(\mathbf{r})=0 \\ \left[\frac{4}{\xi+\eta}\left(\frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}\right) +\frac{1}{\xi\eta}\frac{\partial^2}{\partial \phi^2}+k^2-\frac{2}{\xi+\eta}U_0\right]\psi_c(\xi, \eta)=0 \end{gather} となります。両辺に$\frac{\xi+\eta}{4}$を掛けて、 \begin{align}\label{e4} \left[\frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{1}{4} k^2\xi+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{1}{4} k^2\eta-\frac{U_0}{2}\right]\psi_c(\xi, \eta)=0 \end{align} を得ます。ここで分離定数$\tilde{\nu}_1, \tilde{\nu}_2$を導入します。分離定数は、 \begin{align} \frac{U_0}{2}=\tilde{\nu}_1+\tilde{\nu}_2 \end{align} を満たすように決定します。

今、式\eqref{e4}の鍵括弧内の演算子は$\xi$と$\eta$の部分で独立しており、それぞれの和で書けています。この場合、解は変数分離可能として考えて、 \begin{align} \label{psicx} \psi_c(\xi, \eta)=f(\xi)g(\eta) \end{align} と書きます。代入して整理しますと、 \begin{align} \left\{ \begin{aligned} & \left[\frac{d}{d \xi}\xi\frac{d}{d \xi}+\frac{1}{4} k^2\xi-\tilde{\nu}_1\right]f(\xi)=0\\ & \left[\frac{d}{d \eta}\eta\frac{d}{d \eta}+\frac{1}{4} k^2\eta-\tilde{\nu}_2\right]g(\eta)=0 \\ & \tilde{\nu}_1+\tilde{\nu}_2=\gamma k \end{aligned} \right. \label{e7} \end{align} を得ます。ここで、 \begin{align} \gamma\equiv\frac{U_0}{2k}=\frac{q_Aq_B}{4\pi\varepsilon_0}\frac{1}{\hbar\nu}=\frac{q_Aq_B}{4\pi\varepsilon_0}\frac{\mu}{\hbar^2 k} \end{align} と置きました。$\gamma$はSommerfeld parameterと呼ばれる無次元量で、系にとって低エネルギー散乱かどうかを特徴づけたりする量です。また$\nu=\frac{\hbar k}{\mu}$は２粒子間の相対速度を表しています。

では、式\eqref{e7}を解いていきましょう。解くためには境界条件\eqref{bc}を考えます。 今、入射平面波は波数$k$を持って$z\to-\infty$から平面波$e^{ikz}$として入射してくることを考えています。この条件を放物座標系で考えると \begin{align} \psi_c(\mathbf{r})|_{z\to -\infty}&=e^{ikz}\nonumber\\ &=\exp\left(\frac{1}{2}ik(\xi-\eta)\right) \label{bcp} \end{align} と書けます。今$\xi, \eta \geq 0$なので、$z\to -\infty$を表現するのは、$\eta\to\infty$の領域しかありません。 つまり、$z\to-\infty$は$\eta\to\infty$に対応します。ただし$\xi$については制限がありません。

以上より、境界条件\eqref{bcp}は下記の通りに解釈することができます。

• $\eta$方向の関数$g(\eta)$は、$\eta\to\infty$で$e^{-ik\eta/2}$の形を持たなくてはならない
• $\xi$方向の関数$f(\xi)$は、$\xi$の至るところで$e^{ik\xi/2}$の形を持たなければならない

よって、境界条件の考察から$\xi$方向の解は \begin{align}\label{e8} f(\xi)=e^{ik\xi/2} \end{align} だと考えられます。

解が式\eqref{e8}であるとして、式\eqref{e7}の第1式に代入してみましょう。 式\eqref{e7}の第1式のなかで、分離定数だけがまだ未定ですのでこれを導いてみます。 すると、 \begin{align} \left[\frac{d}{d \xi}\xi\frac{d}{d \xi}+\frac{1}{4} k^2\xi-\tilde{\nu}_1\right]e^{ik\xi/2}=0 \end{align} より、 \begin{align} \left(\frac{1}{2}ik-\tilde{\nu}_1\right)e^{ik\xi/2}=0 \label{e9} \end{align} となります。式\eqref{e9}は$\xi$に依らずいつも成立していなければならないため、左辺の括弧が常にゼロでなければなりません。 よって分離定数$\tilde{\nu}_1$は下記の値を持たなければなりません。 \begin{align} \tilde{\nu}_1=\frac{1}{2}ik \end{align}

$\tilde{\nu}_1$が分かったので\eqref{e7}の第3式より、もう一つの分離定数$\tilde{\nu}_2$も \begin{align} \tilde{\nu}_2&=\gamma k -\tilde{\nu}_1 \nonumber \\ &=\gamma k -\frac{1}{2}ik \end{align} と判明します。

最後に$\eta$方向の微分方程式\eqref{e7}の第2式を解きましょう。 $\eta$方向は$\eta\to-\infty$で$e^{-ik\eta/2}$の形を持たなければならないため、分かっている部分を下記の形だと仮定し、$h(\eta)$について解いていきます。 \begin{align} \label{gh} g(\eta)=h(\eta)e^{-ik\eta/2} \end{align}

式\eqref{e7}の第2式に代入して$h(\eta)$について微分方程式を考えると \begin{align} \left[\frac{d}{d \eta}\eta\frac{d}{d \eta}+\frac{1}{4} k^2\eta-\tilde{\nu}_2\right]\cdot \bigl(h(\eta)e^{-ik\eta/2}\bigr)=0 \end{align} より \begin{align}\label{ghsub} e^{-ik\eta/2}\left[\eta\frac{d^2h(\eta)}{d \eta^2}+(1-ik\eta)\frac{d h(\eta)}{d\eta}-\gamma k h(\eta)\right]=0 \end{align} となりますが、式\eqref{ghsub}はいかなる$\eta$についても成立しなければならないため、 \begin{align} \label{hetadiff} \left[\eta\frac{d^2}{d \eta^2}+(1-ik\eta)\frac{d}{d\eta}-\gamma k\right]h(\eta)=0 \end{align} が成立していなければなりません。これが解ければ、式\eqref{gh}に代入して$g(\eta)$を解くことができます。

微分方程式\eqref{hetadiff}の形は、Kummer-Laplaceの微分方程式として知られ、その解は合流型超幾何関数(Confluent hypergeometric function)として知られています。 式\eqref{hetadiff}は二階線形偏微分方程式なので、２つの独立な式が現れ、一般解はその２式の線形結合で書くことができます。 その2つの独立な式の例として『原点正則な解』と『原点非正則な解』の２つが選ばれます。物理学で興味がある解は、関数が発散しない『原点正則な解』です。 合流型超幾何関数の中の原点正則な解は$M(a,b,z)$と書かれるので、$h(\eta)$は下記のように書かれます。 \begin{align} \label{heta} h(\eta)=cM(-i\gamma, 1,ik\eta) \end{align} ここで、$M(a,b,0)=1$を満たし⁷、$c$は規格化定数です。これで$h(\eta)$が求まりました。

以上から、散乱解\eqref{psicr}は、式\eqref{psicx}, \eqref{gh}, \eqref{heta}より \begin{align} \psi_c(\mathbf{r})&=\psi_c(\xi, \eta) \nonumber\\ &=ce^{ik\xi/2}e^{-ik\eta/2}M(-i\gamma, 1,ik\eta) \nonumber\\ &=c e^{ikz}M(-i\gamma, 1,ik\eta) \label{psisol} \end{align} となります。

4. 散乱状態の漸近形 #

現在の問題を図示しておくと、このように表されます。

4.1. 関数の漸近形 #

続いて散乱状態が原子核から離れた領域でどのような解を持つか調べてみましょう。 なぜ漸近形を考えるのか、その理由として下記のような理由が挙げられます。

• 解\eqref{psisol}を見ても抽象的で分からないため
• 応用を考えた場合に原子核から離れたところだけクーロンポテンシャルと見なせる問題があり、それに将来的に繋げるため (詳細は4.3.2へ)
• 規格化定数$c$を求めるため
  • 具体的には解\eqref{psisol}の$z\to-\infty$で漸近系を求めると、その漸近系には$e^{ikz}$を含む項が現れるはずなので、その係数が1となるように$c$を決定します。

解\eqref{psisol}の漸近形を調べるためには、合流型超幾何関数$M(a,b,z)$の漸近形を知る必要があります。 $M(a,b,z)$の漸近形は参考文献⁸のEq. (13.5.1)より、

と書けます。ここで、$(a)_n$はポッホハマーの記号で、参考文献⁸のEq. (6.1.22)より \begin{align} (a)_n =a(a+1)(a+2)\cdots(a+n-1) =\frac{\Gamma(a+n)}{\Gamma(a)}, ~~(a)_0=1 \end{align} という意味を持ちます。

合流型超幾何関数の引数が$M(-i\gamma, 1,ik\eta)$の場合、$\arg(ik\eta)=\pi/2$なので 式\eqref{Masy}が利用できます。つまり \begin{align} &\hspace{-2em}M(-i\gamma, 1,ik\eta)\Bigr|_{\eta\to\infty} \nonumber\\ &\hspace{-3em}= \frac{\Gamma(1)}{\Gamma(1+i\gamma)}e^{\pi \gamma}(ik\eta)^{i\gamma}\sum_{n=0}^{\infty}\frac{(-i\gamma)_n(-i\gamma)_n}{n!}(-ik\eta)^{-n} +\frac{\Gamma(1)}{\Gamma(-i\gamma)}e^{ik\eta}(ik\eta)^{-i\gamma-1}\sum_{n=0}^{\infty}\frac{(1+i\gamma)_n(1+i\gamma)_n}{n!}(ik\eta)^{-n} \\ &\hspace{-3em}= \frac{e^{\pi \gamma}}{\Gamma(1+i\gamma)}(ik\eta)^{i\gamma }\sum_{n=0}^{\infty}\frac{{(-i\gamma)_n}^2}{n!}(-ik\eta)^{-n} +\frac{e^{ik\eta}}{\Gamma(-i\gamma)}(ik\eta)^{-i\gamma}\sum_{n=0}^{\infty}\frac{{(1+i\gamma)_n}^2}{n!}(ik\eta)^{-n-1} \end{align} となります。複素数の関係式 \begin{align} z^c=\exp(c\ln z)=\exp\left[c(\ln|z|+i\arg z)\right] \end{align} を用いると、乗数について下記の変形が可能です。 \begin{align} (ik\eta)^{i\gamma}&=\exp\left[i\gamma\left\{\ln(k\eta)+i\frac{\pi}{2}\right\}\right] \\ (ik\eta)^{-i\gamma}&=\exp\left[-i\gamma\left\{\ln(k\eta)+i\frac{\pi}{2}\right\}\right] \end{align} ここで、$k>0, \eta>0$の事実を用いています。式変形を続けると \begin{align} &M(-i\gamma, 1,ik\eta)\Bigr|_{\eta\to\infty} \nonumber \\ &= \frac{e^{\pi\gamma/2}}{\Gamma(1+i\gamma)}\exp\bigl[i\gamma\ln(k\eta)\bigr] \sum_{n=0}^{\infty}\frac{{(-i\gamma)_n}^2}{n!}(-ik\eta)^{-n} -\frac{e^{\pi\gamma/2}e^{ik\eta}}{\Gamma(-i\gamma)}\exp\bigl[-i\gamma\ln(k\eta)\bigr] \sum_{n=0}^{\infty}\frac{{(1+i\gamma)_n}^2}{n!}(ik\eta)^{-n-1} \\ &= \frac{e^{\pi\gamma/2}}{\Gamma(1+i\gamma)}\exp\bigl[i\gamma\ln(k\eta)\bigr] \left[1+\frac{\gamma^2}{ik\eta}+O((k\eta)^{-2})\right] -\frac{e^{\pi\gamma/2}}{\Gamma(-i\gamma)}\exp\bigl[ik\eta-i\gamma\ln(k\eta)\bigr] \frac{1}{ik\eta}\left[1+\frac{(1+i\gamma)^2}{ik\eta}+O((k\eta)^{-2})\right] \label{Masy2} \end{align} となります。この展開を解\eqref{psisol}に代入し、$\eta\to\infty$を考えれば、 \begin{align} \psi_c(\mathbf{r})|_{\eta\to\infty}&=c \frac{e^{\pi\gamma/2}}{\Gamma(1+i\gamma)}\exp\bigl[ikz+i\gamma\ln(k\eta)\bigr] \left[1+\frac{\gamma^2}{ik\eta}+O((k\eta)^{-2})\right] \nonumber \\ &+ c\frac{e^{\pi\gamma/2}}{\Gamma(-i\gamma)}\exp\bigl[ik(z+\eta)-i\gamma\ln(k\eta)\bigr] \frac{1}{ik\eta}\left[1+\frac{(1+i\gamma)^2}{ik\eta}+O((k\eta)^{-2})\right] \end{align} を得ます。 通常、第二項の中括弧内のオーダーは、第二項の係数にかかっている$\eta^{-1}$を考えて$O((k\eta)^{-1})$までで良いですが、折角なので書いておきます。

入射波と球面波の表現にするため, $\eta=r-z=r(1-\cos\theta)=2r\sin^2\frac{\theta}{2}$を用いると \begin{align} \psi_c(\mathbf{r})\Bigr|_{r-z\to\infty} &=c \frac{e^{\pi\gamma/2}}{\Gamma(1+i\gamma)}\exp\bigl[ikz+i\gamma\ln{kr(1-\cos\theta)}\bigr] \left[1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right] \nonumber \\ &+ c\frac{e^{\pi\gamma/2}}{\Gamma(-i\gamma)}\exp\left(ikr-i\gamma\left[\ln(2kr)+\ln\sin^2\frac{\theta}{2}\right]\right) \frac{1}{2ikr\sin^2\frac{\theta}{2}}\left[1+\frac{(1+i\gamma)^2}{ikr(1-\cos\theta)}+\cdots\right]\hspace{3em} \label{psiasy2} \end{align} となります。\eqref{psiasy2}の第一項は平面波、第二項は球面波を表していることが分かります(指数関数の中身の対数を含む部分を消すと明らかになります)。

4.2. 規格化定数の決定 #

規格化として、\eqref{bc}で決めたように入射波の指数関数の係数を1にするようにすれば、 \begin{align} &c \frac{e^{\pi\gamma/2}}{\Gamma(1+i\gamma)}=1,\nonumber \\ &\to c=e^{-\pi\gamma/2}\Gamma(1+i\gamma) \end{align} と決めればよい、と分かります。このように$c$を決めると下記の通りに変形できます。 \begin{align} \hspace{-2em}\psi_c(\mathbf{r})\Bigr|_{r-z\to\infty} &=\exp\bigl[ikz+i\gamma\ln{kr(1-\cos\theta)}\bigr] \left[1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right] \nonumber \\ &+ \frac{\Gamma(1+i\gamma)}{\Gamma(-i\gamma)}\frac{1}{2ik\sin^2\frac{\theta}{2}} \exp\left(-i\gamma\ln\sin^2\frac{\theta}{2}\right) \frac{\exp\left[ikr-i\gamma\ln(2kr)\right]}{r} \left[1+\frac{(1+i\gamma)^2}{ikr(1-\cos\theta)}+\cdots\right]\hspace{3em} \\ &\hspace{-6em}\mbox{$\Gamma(1+z)=z\Gamma(z)$より$\Gamma(-i\gamma)=\frac{\Gamma(1-i\gamma)}{-i\gamma}$の関係式を用いて} \nonumber \\ &=\exp\bigl[ikz+i\gamma\ln{kr(1-\cos\theta)}\bigr] \left[1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right] \nonumber \\ &+ \frac{\Gamma(1+i\gamma)}{\Gamma(1-i\gamma)}\frac{-\gamma}{2k\sin^2\frac{\theta}{2}} \exp\left(-i\gamma\ln\sin^2\frac{\theta}{2}\right) \frac{\exp\left[ikr-i\gamma\ln(2kr)\right]}{r} \left[1+\frac{(1+i\gamma)^2}{ikr(1-\cos\theta)}+\cdots\right]\hspace{3em} \end{align} ここで、クーロン散乱振幅(Coulomb-scattering amplitude) \begin{align} \label{csa} f(k,\theta)\equiv \frac{-\gamma}{2k\sin^2\frac{\theta}{2}} \exp\left[-i\gamma\ln\left(\sin^2\frac{\theta}{2}\right)\right]\frac{\Gamma(1+i\gamma)}{\Gamma(1-i\gamma)} \end{align} を定義して \begin{align} \psi_c(\mathbf{r})\Bigr|_{r-z\to\infty} &=\exp\bigl[ikz+i\gamma\ln{kr(1-\cos\theta)}\bigr] \left[1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right]\nonumber \\ &\hspace{3em}+ f(k,\theta) \frac{\exp\left[ikr-i\gamma\ln(2kr)\right]}{r} \left[1+\frac{(1+i\gamma)^2}{ikr(1-\cos\theta)}+\cdots\right] \hspace{1em}\label{end} \end{align} を得ます。漸近でのオーダーを揃えるならば \begin{align} \psi_c(\mathbf{r})\Bigr|_{r-z\to\infty} &=\exp\bigl[ikz+i\gamma\ln{kr(1-\cos\theta)}\bigr] \left[1+\frac{\gamma^2}{ikr(1-\cos\theta)}+\cdots\right]\nonumber \\ &\hspace{3em}+ f(k,\theta)\frac{\exp\left[ikr-i\gamma\ln(2kr)\right]}{r} \end{align} です。

以上でここまでで導出は終わりです。

4.3. 補足 #

少し補足していきましょう。

4.3.1. クーロン散乱振幅 #

式\eqref{csa}で現れたクーロン散乱振幅(Coulomb-scattering amplitude)は、どのくらいの速度$k$で入射し、どの方向$\theta$に反射する時にどのくらい散乱するか？という量を表しています。これは、$\theta\to 0, \pi$で発散してしまうのが特徴です。

\eqref{end}の1行目、2行目に中に含まれる指数関数内の対数と、そのあとの括弧内の1以外をとりあえず無視すると、 1, 2行目はそれぞれ$e^{ikz}, \frac{e^{ikr}}{r}$になり、z軸正の向きに進む平面波、外向きの球面波を表していそうなことが分かります。 しかし、指数関数の中身は対数の発散であるため、どれだけ離れたとしても完全な平面波として記述することができません。

平面波として記述出来ないにしても、非常に大きい$\eta=r-z$に対して、クーロンポテンシャルによる影響は波動関数の位相に対してのみ影響します($\gamma\ln(kr(1-\cos\theta))$が全て実関数であるためです)。つまり、第一項の波形が歪んでいるとはいっても、位相だけなので、絶対値をとれば消えてしまいます。

流束(確率の流れ)$\mathbf{j}(\mathbf{r})$を計算すれば、単なる平面波の結果と同じとなります。

4.3.2. 漸近形が重要である理由 #

さて、散乱状態$\psi_c(\mathbf{r})$の漸近形が物理学では興味を持たれます。 なぜ漸近形が重要なのか説明しましょう。 今はクーロンポテンシャルであり、解は\eqref{psisol}として全領域で解けてしまう数少ない問題です。 一般的には原子核周辺ではクーロンポテンシャルではなく、非常に遠い領域のみでクーロンポテンシャルと見なせる場合が多いです。 散乱した結果を観測するためには、基本的に原子核の大きさよりも十分離れた距離で見るため、その領域ではクーロンポテンシャル下の微分方程式の線形結合となります。

なので漸近形が重要なのです。

5. 参考文献、脚注 #