クーロンポテンシャルによる散乱（量子力学）

詳細

本稿では概要だけを説明し、導出過程や詳細は以下のpdfで説明します。
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/scattering_coulomb.pdf

概要

電荷\(q_A\)を持つ原子核に、遠方から\(q_B\)を持つ電子が衝突する過程を考えます。
例えば、水素原子の原子核である陽子1個(\(q_B=+e\), eは電気素量)に対し、遠方から電子(\(q_A=-e\))が衝突する過程です。
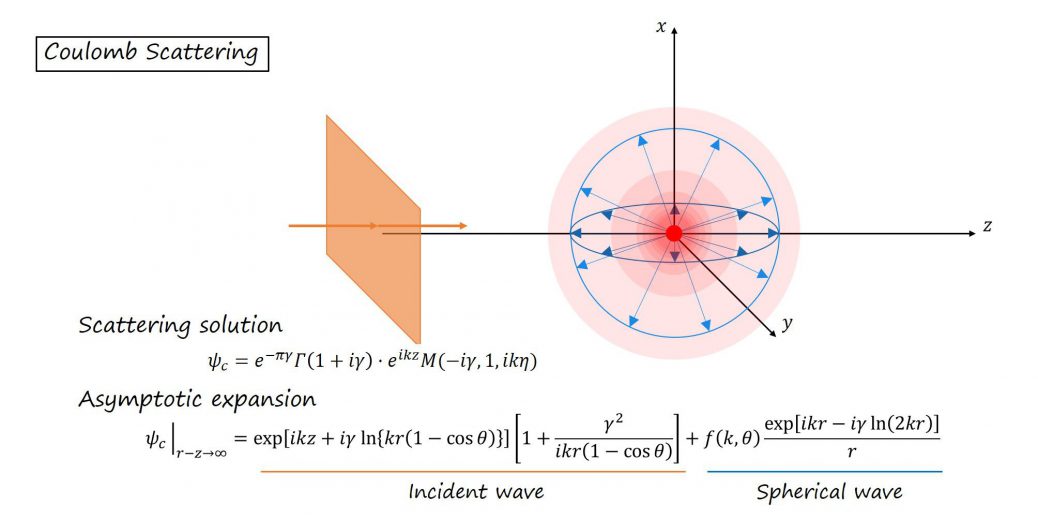
図で表せばこのような感じです。

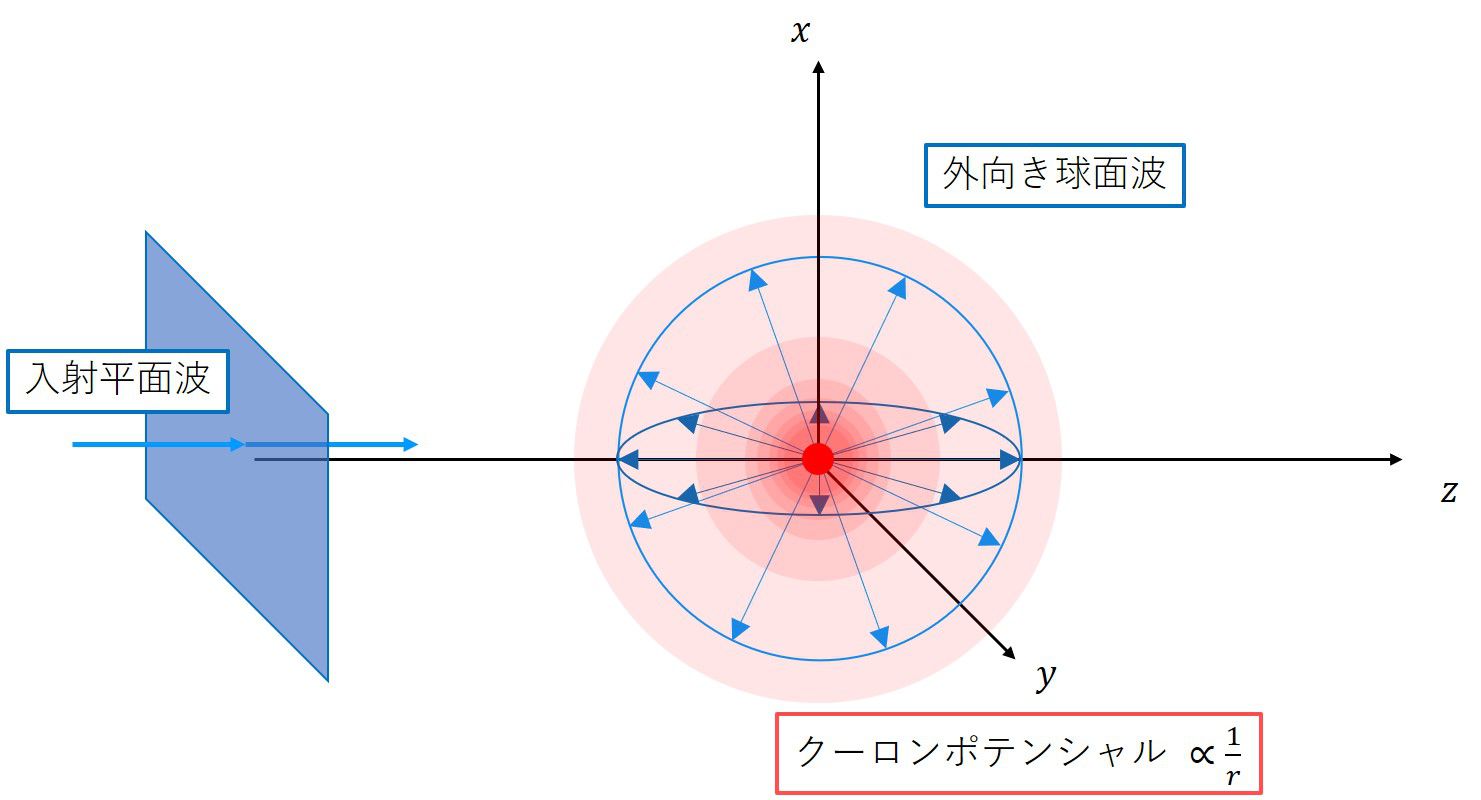
相対座標に対する時間依存しないシュレーディンガー方程式は、

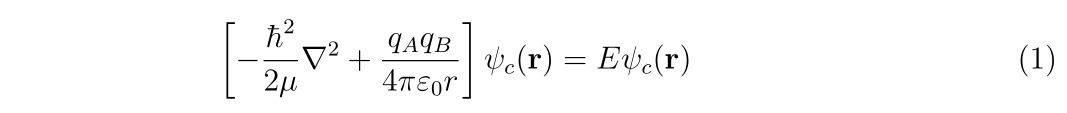
と書くことができます。ここで、\(\hbar\)はプランク定数、\(\varepsilon_0\)は真空の誘電率、\(\mu\)はAとBの換算質量を表し, \(E\)は衝突のエネルギーを表します。
簡単にするために係数をまとめて

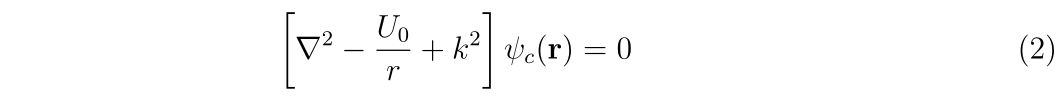
と書きます。ここで、

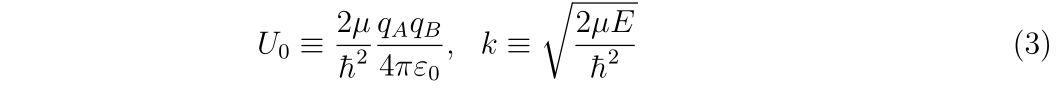
という量を定義しました。
これから、波数\(k\)で定義される平面波が入射したらどのように応答するか？を知りたいので、式(1)を境界条件

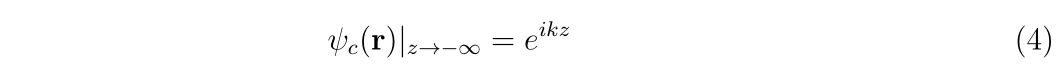
の下で解いていきます。

導出した結果は、

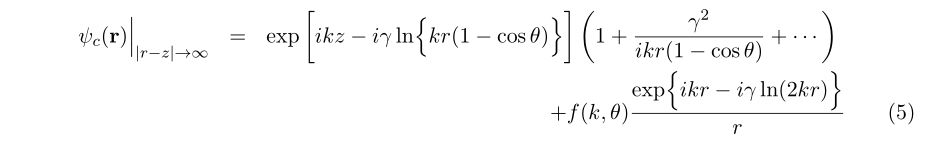
となります。この展開は\(|r-z|\to 0\)となる\(z\)軸上もしくはz軸近傍では使えないことを注記しておきます。元々の境界条件(4)は、\(z\to -\infty\)だけで決まっており\(x,y\)には条件はありませんが、結論として得られるものは\(z\)軸からは離れた領域でなければならない、とより制限された範囲でのみ導ける、となっています。

ここで

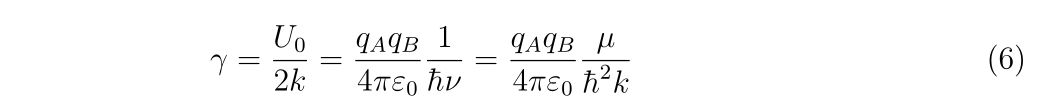
であり、\(\gamma\)はSommerfeld parameterと呼ばれる量であり、\(\nu=\frac{\hbar k}{\mu}\)は２粒子間の相対速度を表しています。また、

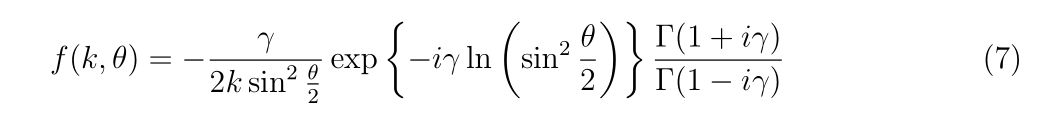
はクーロン散乱振幅と呼ばれる量であり、波数\(k\)を持って入射した平面波が、入射方向に対して角度\(\theta\)方向にどれだけ球面波が歪むか？を表す量です。