問題
水素原子の電子の基底状態において、原点に電子を見出すことができるでしょうか?
問題設定
非相対論の範囲で、水素原子の電子を考えます。
電子の満たすシュレーディンガー方程式は、プランク定数\(\hbar\),電子の電荷\(e\),電子の質量\(m\)
をそれぞれ\(\hbar=1, e=1, m=1\)とする原子単位系で

と書けます。ここで、\(\nabla\)はデカルト座標系\((x,y,z)\)における微分演算子\(\nabla=\left(\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z} \right)\)であり、\(\psi(\mathbf{r})\)は波動関数を表します。
規格化は
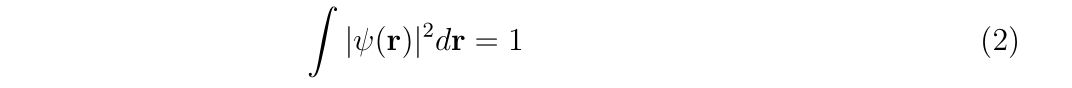
で行います。特に、これから中心力に対する問題を考えていくので、球面座標系で変数分離を考えます。球面座標系において動径方向\(r(=\sqrt{x^2+y^2+z^2})\)と角度方向\(\theta(=\cos^{-1}(z/r)), \varphi((=\tan^{-1}(y/x)))\)の\((r,\theta, \varphi)\)座標における波動関数は
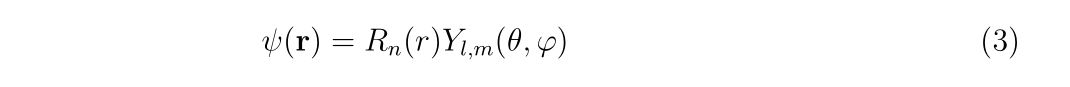
と書きます。ここで規格化は

とします。過程は飛ばしますが、シュレーディンガー方程式の固有値\(E=-1/2\)に属する基底状態の波動関数は、量子数\((n, l, m)=(1,0,0)\)を持つ状態として指定され、\(R(r)\)は

と書けます。\(\theta, \varphi\)方向の関数は\(Y_{0,0}=({4\pi})^{-1/2}\)ですので、波動関数は
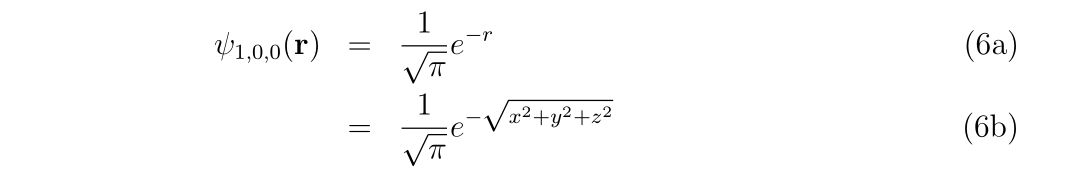
となります。
さて、存在確率密度はどう考えればよいでしょう?
まず規格化から、
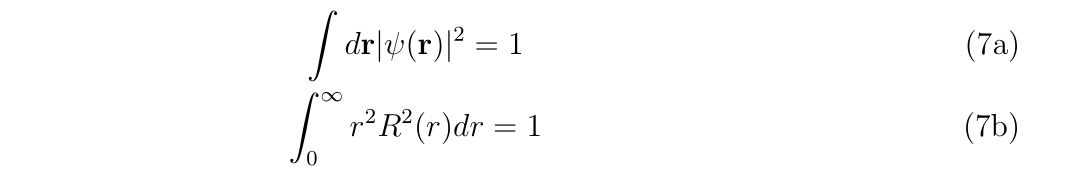
と計算されるわけですから、原点からの距離\(r\sim r+dr\)の範囲に電子を見出す存在確率密度\(f(r)dr\)の係数\(f(r)\)は
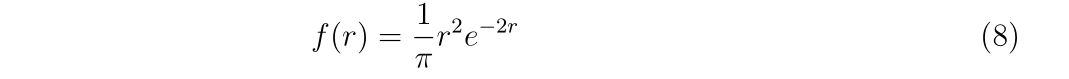
と書けます。
一方、存在確率密度は波動関数の絶対値二乗ですので、

ですから、位置\((x,y,z)\sim (x+\Delta x,y+\Delta y,z+\Delta z)\)の範囲に見出す確率\(g(x,y,z)dxdydz\)の係数\(g(x,y,z)\)は
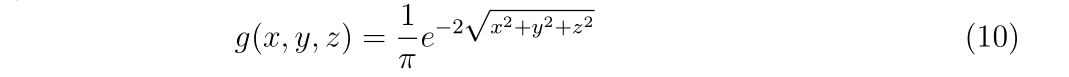
と書けます。
さて、ここで疑問が生じます。原点\((x,y,z)=(0,0,0)\)において、電子を見出す可能性はあるのでしょうか?
つまり、動径方向の関数については原点における\(f(0)\)は式(8)より

であり、\(g(0,0,0)\)は式(10)より
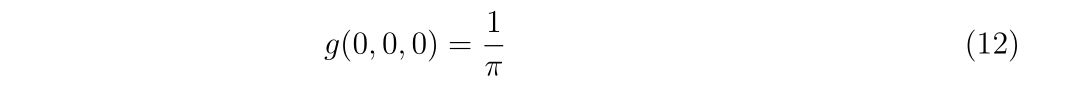
と書けるのでどちらが正しいのか?本当に観測を行ったとき、原点で電子を見出すことはあるのか?
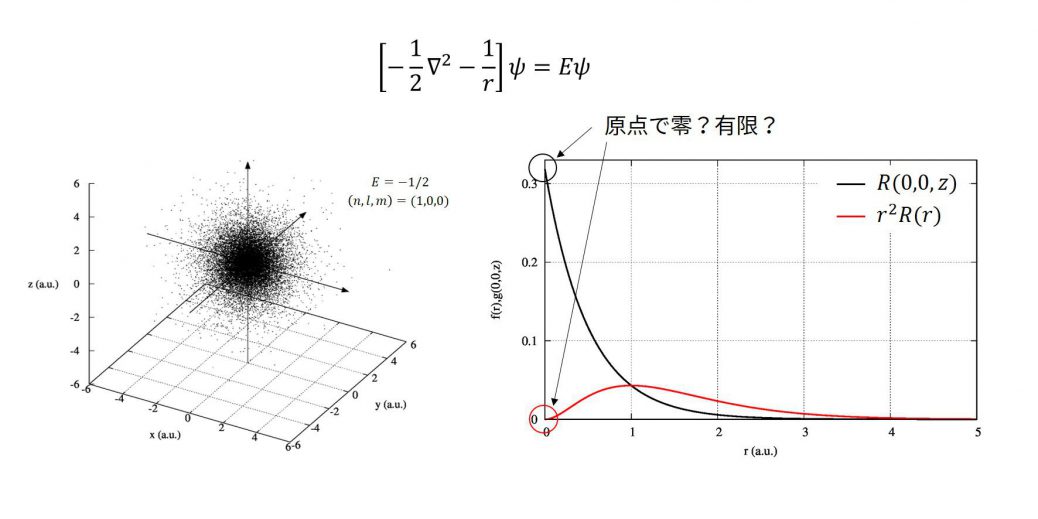
という問題です。つまり、グラフにすると以下のようになります。\(g(x,y,z)\)については、\(x=y=0\)としてグラフにしています。
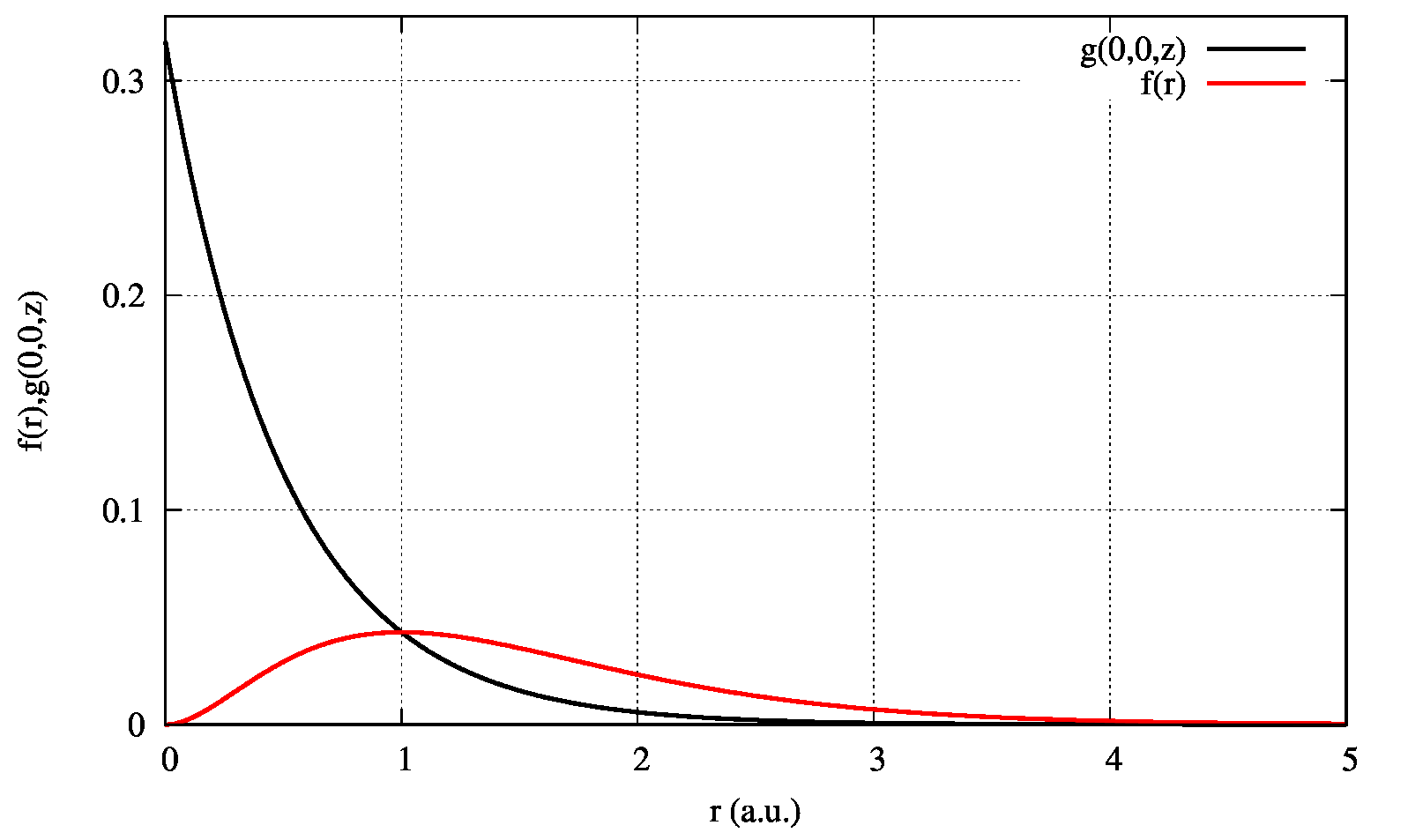
これで注目するのは、原点における値がゼロか有限か?で大きく異なっている点です。
座標系が違うだけで物理が変わることはありませんので、これは解釈の問題です。
現実には原点には原子核があるので原点における電子を観測することはできないので、頭の中で考えます。
結論としては、どちらも正しくて解釈が異なる。そして、原点で電子を見出すことがあっても良いです。
その理由を述べていきます。
考察
まず、数値実験を行い事実を確認します。
デカルト座標系\((x,y,z)\)における波動関数\(\psi(\mathbf{r})=\frac{1}{\sqrt{\pi}}e^{-\sqrt{x^2+y^2+z^2}}\)は紛れもない事実ですので、フォン・ノイマンの棄却法に従って、\((x,y,z)\)空間で一様な変数を作り出し、この確率密度に従った乱数を表示させます。すると以下のような図を得ます。
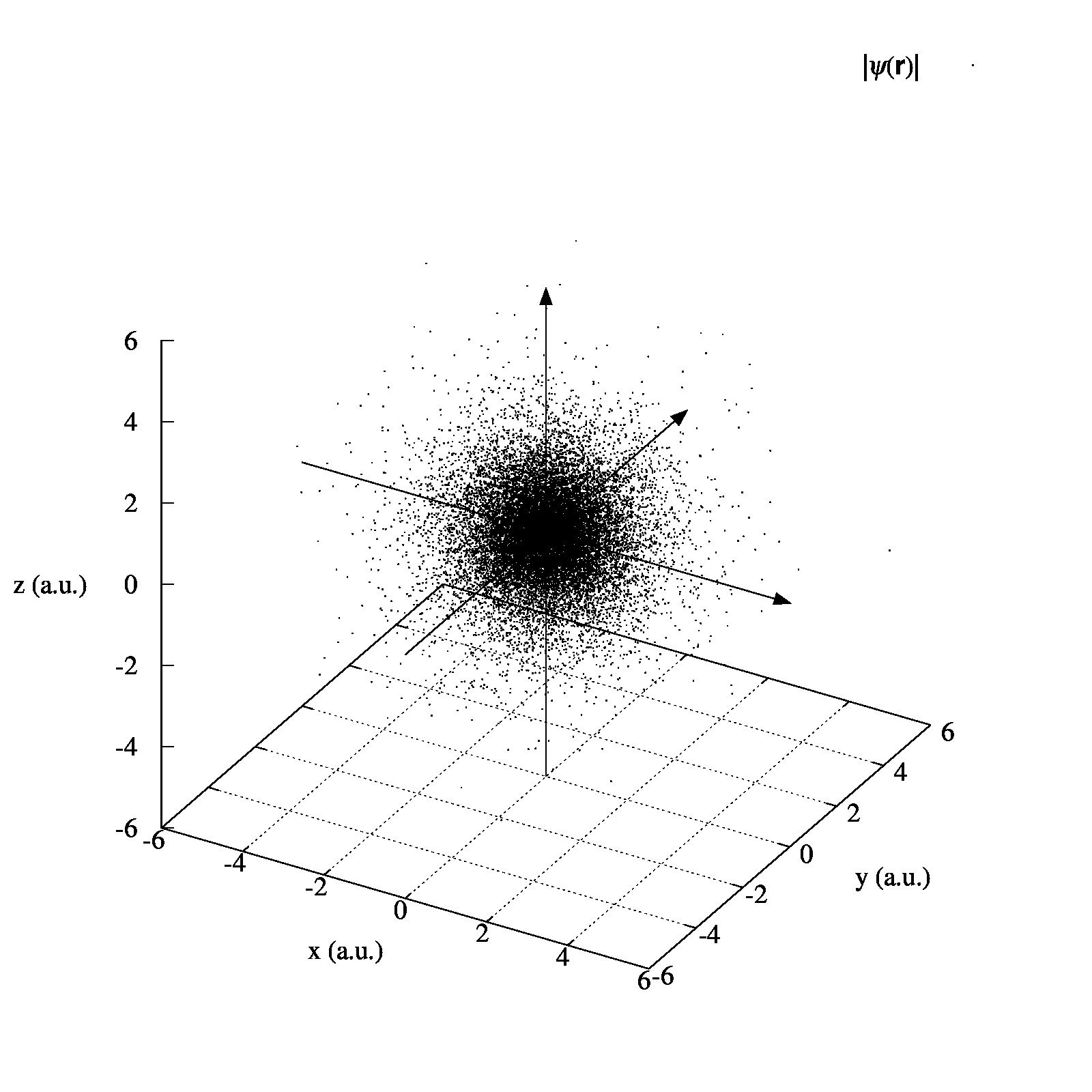
例えば\(x=0, y=0\)に固定してz軸上の波動関数は、
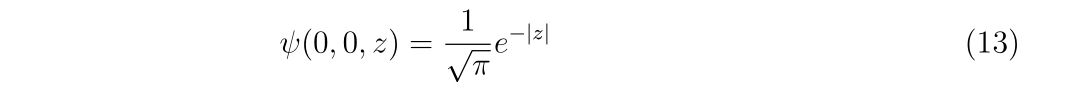
となりますので、\(z=0\)においてゼロではない有限の値をとるため確率密度が存在しそうなので、原点に電子を見出してもよさそうです。
続いて動径方向の分布を考えましょう。棄却法によって採用された\(n\)番目の点\((x_n,y_n,z_n)\)(図に表示されている点)の原点からの距離\(r_n=\sqrt{x_n^2+y_n^2+z_n^2}\)を調べてみます。そして、\(r\sim r+\Delta r\)の範囲にある点数を数え、観測された個数と原点からの距離の関数を考えます。これは動径分布関数の\(f(r)\)に等しいはずです。すると、以下のような図を得ます。
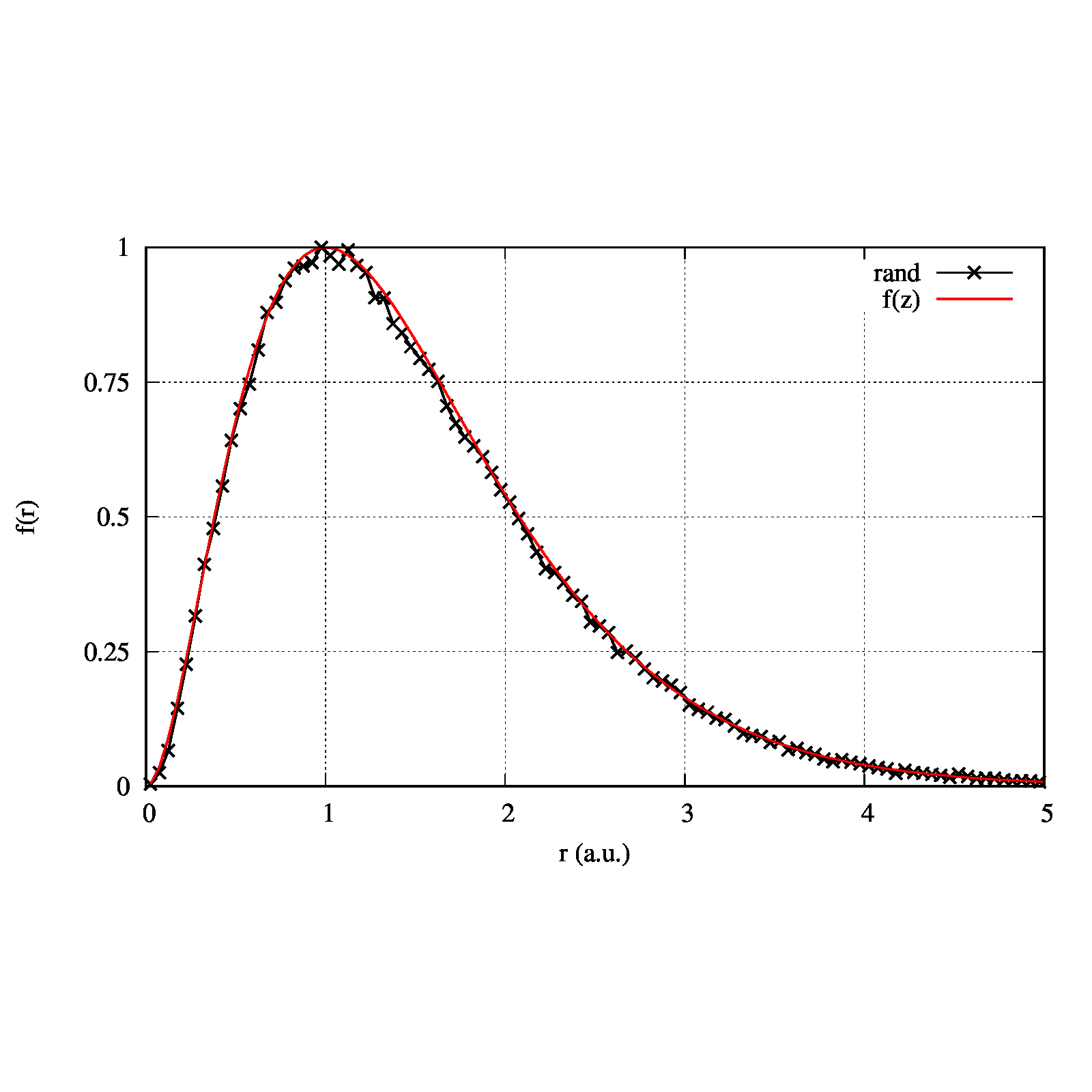
確かに、確率密度の係数にかかる分布\(f(r)\)になっていることが分かります(最大値を1にするように規格化しています)。
さて、以上の数値実験からやはりどちらも数式通りであり、正しいことが分かりました。
すると解釈の問題でしょう。どのように解釈していけばよいかを考えていきます。
まず動径方向の確率密度\(f(r)dr=r^2R^2(r)dr\)ですが、これは正確には

と書いたほうが良いでしょう。意味は、半径が\(r\sim r+dr\)の間を占める球殻の体積は\(4\pi r^2 dr\)であり、その体積の中に粒子の見出しやすさ\(\frac{R^2(r)}{4\pi}\)が掛かっている、という意味です。
半径が\(r\to 0\)の極限において、式を解釈すると、
球殻の体積がゼロのとき、その中に粒子を見出す確率はいくつか?
という問いになります。見出すことができる体積はゼロなので、体積ゼロの領域に電子を見出すことはできません。なので、
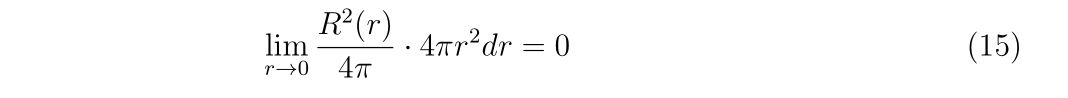
となります。すなわち、\(r^2 dr\)の部分がゼロになるだけで、\(R^2(r)\)の部分は値を持っていても良い、ということになります。少し詳しく言えば、球殻の体積がゼロの時に確率があると確率が無限大になってしまうので、少なくとも\(r\to 0\)で\(R(r)\propto r^{n},~(n>-1)\)であることが課されます。
以上の話が正しければ、原点では体積がゼロなので、電子を見出す確率\(r^2R^2(r)\)は\(r=0\)でゼロ、すなわち電子を見出さない、という結論になりそうです。
これまでの考察を行っても矛盾が生じたままで、何一つ解決していません。
「原点において電子を見出す体積がゼロだから、電子を見出せない」という結論が誤りなのか、もう少し疑ってみます。
体積がゼロでも電子を見出すことがあり得ることを仮定した場合、これはどういう意味を持つでしょうか。
2つの解釈を説明します。
- 有限の大きさによって、本当の原点に電子を見出すことはない
- 点で電子を見出すか、密度を考えるかで区別しなければならない
例えば将来的に超高精度な観測機器ができた場合、原点に電子を見出す場合にしても、現実ではどう頑張ってもプランク長(10^{-35}\mathrm{m})以上の分解能は無いはずです(電子の大きさもありますしね。しかもプランク長以下の長さは物理的な意味がないと言われています。一応、プランク長よりも短くなる長さがあるようですが、無限小よりかは大きいでしょう)。なので、原点に電子を見出した!と思っても、実は原点からほんのちょっとずれているのかもしれません。
だから、本当の原”点”に電子は見出さないのかもしれません。
点自体に体積は無いので、確率密度がゼロだからと言って原点に電子を見出しても良い
二番目の点自体に体積は無いので、確率密度がゼロだからと言って原点に電子を見出しても良い、が正しいと思いますが…すみません。調べたりしたのですが、なかなか目当ての問題や解答がなく、探すのを諦めました。
存在確率密度なので、(体積中の電子を見出す確率)/(見出す体積)ですが、原点であればこの分母がゼロです。
この場合に、原点に電子を見出したからと言って、それは体積でも何でもない0次元の情報ですから、確率「密度」の情報に対応させることができません。なので見出しても問題がないと考えます。
一方、原点以外で波動関数の節となる確率密度がゼロになる点においては体積が有限であり、その点では本当に見出すことは本当の意味でありません。
結論
点自体に体積は無いので、確率密度がゼロだからと言って原点に電子を見出しても良い。
…で合っていると思いますが、明確な参考文献を見つけられませんでした。
メモとして、これまでの考察を書きました。
補足)カスプについて
一つ、本当の原点に電子を見出してしまった場合、ポテンシャルエネルギーが発散しないのか心配になります。
すなわち、ポテンシャルエネルギー項が\(-\frac{1}{r}\)であり、無限大になるので非物理的な気がします。
だからと言って、ポテンシャルエネルギーが発散するから非物理的である、という結論は間違いです。
この原点における発散はカスプ(Cusp)と呼ばれ、運動エネルギーの項と相殺するため、消えてしまう、もしくは消えなければなりません(カスプ条件)。カスプについて説明するために、もう一度シュレーディンガー方程式に立ち返って考えてみます。
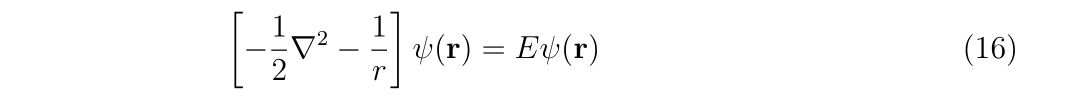
左辺のハミルトニアンのポテンシャル項\(-\frac{1}{r}\)は\(r=0\)で発散しています。しかし束縛状態では、波動関数の二乗は電子の存在確率密度ですので、全空間で積分したら有限にならなければなりません。つまり右辺\(E\psi(\mathbf{r})\)は発散してはなりません。
以上から、\(\psi(\mathbf{r})\)は連続でなければならず、\(r=0\)で

を計算したら\(\frac{1}{r}\psi(\mathbf{r})\)の項が出てきてポテンシャルエネルギーの項を打ち消さなければなりません。
波動関数に課されるこの条件は、カスプ条件と呼ばれます。