まとめ
微分を中心差分に変える
\(
\begin{align}
\frac{d}{dx}\psi(x)&\approx \frac{\psi(x_{i+1})-\psi(x_{i-1})}{2h} \\
\frac{d^2}{dx^2}\psi(x)&\approx \frac{\psi(x_{i+1})-2\psi(x_i)+\psi(x_{i-1})}{h^2}
\end{align}
\)
という操作によって求めたハミルトニアンの行列要素は、空間に局在化した正規直交で選点直交性を持つ基底関数
\(
\begin{eqnarray}
\varphi_i(x)=
\left\{
\begin{aligned}
& \frac{1}{\sqrt{h}} ~~~~~~(x_i-h/2 \lt x \lt x_i+h/2) \\
& \frac{1}{2\sqrt{h}} ~~~~~~(x = x_i\pm h/2) \\
& 0 ~~~~~~(上以外)
\end{aligned}
\right.
\end{eqnarray}
\)
で展開したものと同一です。すなわち、行列要素は
\(
\begin{align}
\langle \varphi_i|\hat{H}|\varphi_j \rangle
&=\int_{-\infty}^{\infty} \varphi_i(x)\left[-\frac{1}{2}\frac{d^2}{dx^2}+V(x)\right]\varphi_j(x)dx\\
&=-\frac{1}{2h^2}\left[\delta_{j,i+1}-2\delta_{j,i}+\delta_{j,i-1}\right]+V(x_j)\delta_{j,i}
\end{align}
\)
と求められます。また、関数\(f(x)\)の期待値は
\(
\begin{align}
&\int_{-\infty}^{\infty} \psi(x) f(x)\psi(x) dx\approx\sum_i f(x_i)
\end{align}
\)
と求められます。
有限差分法で固有値問題を数値計算で解きます。
例として、時間依存しないシュレーディンガー方程式を解いてみます。
同様の方法で波動方程式の固有振動数、固有モードを得ることが出来ます。
wikipediaをはじめとする解説書、解説ページでは、
微分方程式を解くために微分を有限差分近似(差分商)で置き換えて得られる差分方程式で近似する
する解法だ、とあります。
一番簡単な微分を近似する方法としてオイラー法があります。
オイラー法は
\(
\displaystyle \frac{df}{dx}\approx \frac{f(x+\Delta x)-f(x)}{\Delta x}
\)
の形で有限の間隔\(\Delta x\)で微分を差分に置き換える方法です。
この、微分を差分に置き換える近似によって固有値問題である時間依存しないシュレーディンガー方程式
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+V(x)\right]\psi(x)=E\psi(x)
\)
を解きます。二階微分の差分近似式は、一階微分の近似式を2階用います。
すなわち、二階微分は一階微分\(\frac{df}{dx}\equiv g(x)\)の一階微分と表現できるので、前進差分を用いて
\(
\begin{align}
\frac{d^2f}{dx^2}&\approx\frac{d}{dx}\left[\frac{g(x+\Delta x)-g(x)}{\Delta x}\right] \\
\end{align}
\)
と表せます。各々に後退差分を適用すると、
\(
\begin{align}
\frac{d}{dx}g(x+\Delta x)&\approx\frac{f(x+\Delta x)-f(x)}{\Delta x} \\
\frac{d}{dx}g(x)&\approx\frac{f(x)-f(x-\Delta x)}{\Delta x}
\end{align}
\)
より、二階微分は
\(
\begin{align}
\frac{d^2f}{dx^2}\approx\frac{f(x+\Delta x)-2f(x)+f(x-\Delta x)}{\Delta^2}
\end{align}
\)
となります。これを原子単位系のシュレーディンガー方程式に代入すると
\(
\begin{align}
\displaystyle -\frac{1}{2}\frac{\psi(x+\Delta x)-2\psi(x)+\psi(x-\Delta x)}{\Delta x^2}+V(x)\psi(x)=E\psi(x)
\end{align}
\)
より
\(
\begin{align}
-\frac{1}{2\Delta x^2}\psi(x+\Delta x)+\left(\frac{1}{\Delta x^2}+V(x)\right)\psi(x)-\frac{1}{2\Delta x^2}\psi(x-\Delta x)=E\psi(x)
\end{align}
\)
という差分方程式が得られます。
固定端条件(\(\psi(x_0)=\psi(x_{N+1})=0\), 区間\([a\sim b]=[x_0\sim x_{N+1}]\)では)の下で、行列表現では、以下のように書き下せます。
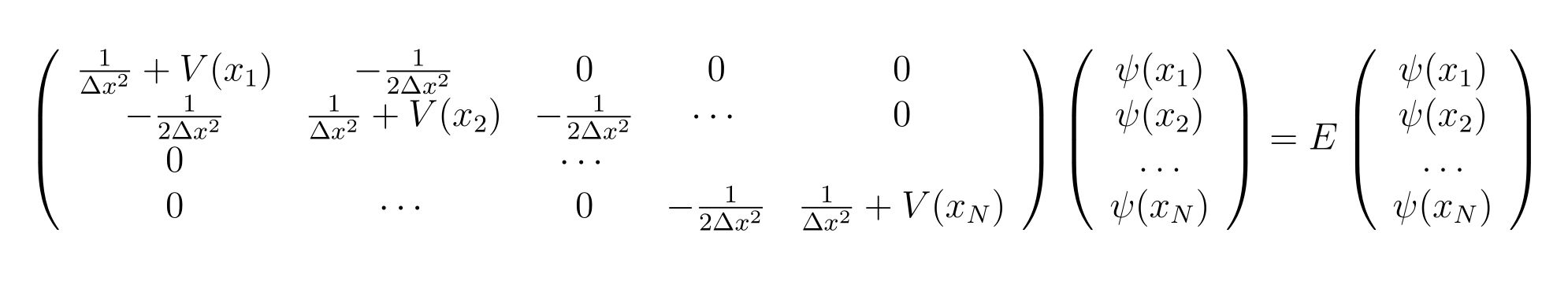
周期境界条件の場合、区間\([a\sim b]=[x_1\sim x_N]\)では、
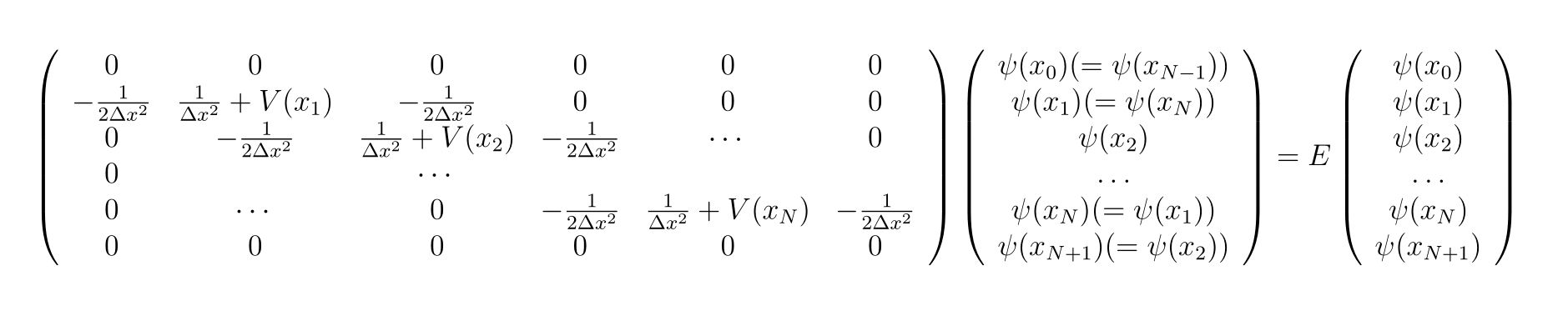
となります。
こののち、左辺を対角化することでエネルギー固有値と固有関数を得ることが出来ます。
差分で対角化→本当に固有値?
さて、以上のように求めた固有値はいったい何なのでしょうか。
何なのでしょうか?とは、
微分を差分で近似して、何か知らないけど対角化した。そしたらエネルギー固有値と固有ベクトルが出てきた。
これは何に基づいた計算なのでしょうか。この方法で求めた固有ベクトルは固有関数に何故一致するのでしょうか。
私はどうもここがすっきりせず、差分による固有値問題の解法が何となく使いたくありませんでした。
ここからは、変分法の原理に基づき、矩形関数による展開を行うと上記の差分による展開式と同じ行列表現が得られることを示していきます。
基底関数による考え
上記の通り、演算子が行列表現として表せるのであれば、それに応じた基底関数があってもおかしくありません。
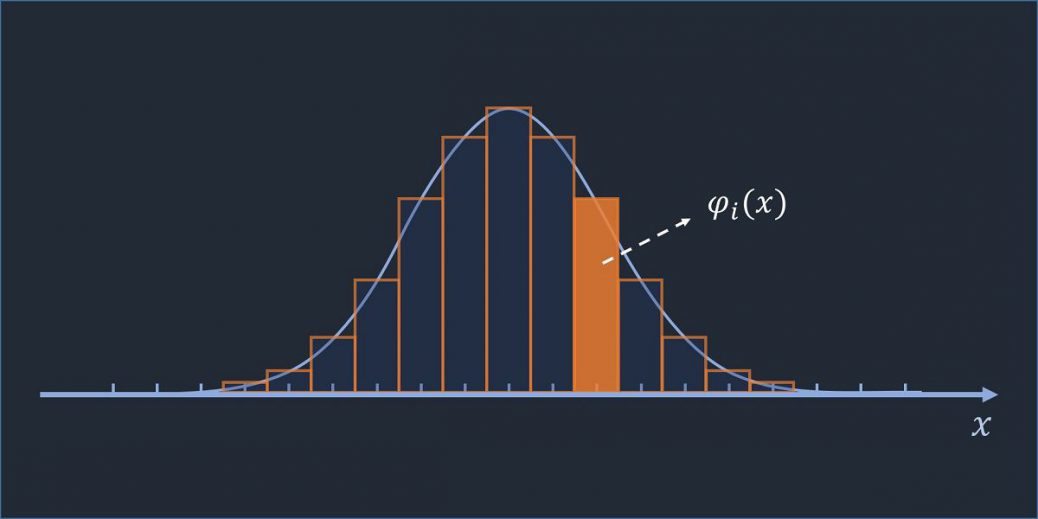
上記のハミルトニアン行列を導き出す方法として、位置的に局在した長方形の関数を考えます。
この基底関数を考えることで上記の行列表現を導くことが出来ます。
空間の離散化
まず、波動関数\(\psi(x)\)をディラックのデルタ関数を用いて
\(
\displaystyle\psi(x)=\int \psi(x’)\delta(x-x’)dx
\)
と表します。これは明らかに成立していますね。右辺を計算すればまさに左辺です。
これは、
空間のある1点\(x\)における波動関数の値\(\psi(x)\)は、関数\(\psi(x’)\)にデルタ関数を掛けて積分したものだ。
と考えることが出来ます。別の言い方をすれば、滑らかな波動関数が無限個の点の集合で書かれているということです。
この、無限個の点の集合を有限個の点の集合と近似して、空間を離散化します。
離散化に物理的な意味は無く、数値計算の都合上と考えてよいです。
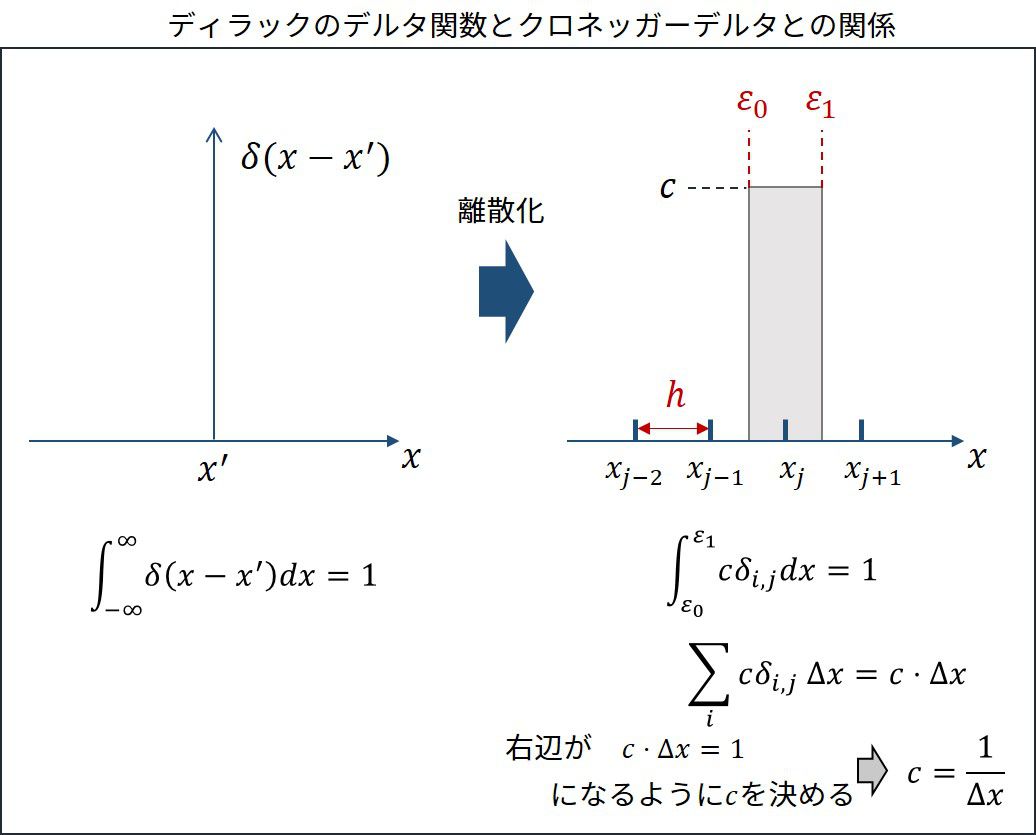
※ここで、\(\Delta x\)と\(h/latex]が混在していますが、どちらも同じものを指します。
いつも[latex]\Delta x=h\)です。
ディラックのデルタ関数と離散化した関数は積分が等しくなるように決めます。
図のように考えますと、結局
\(
\displaystyle \delta(x-x’)\xrightarrow{離散化}\frac{\delta_{i,j}}{\Delta x}
\)
とするのが良いと分かります。ここで、\(\delta_{i,j}\)はクロネッガーのデルタを表し、\(x\)を離散化した座標\(x_i\)がある座標\(x_j\)に等しい時だけ値\(1\)を持つことを意味します。それ以外はゼロです。
以上の事から、空間の離散化はクロネッガーのデルタを用いて表現できることが分かりました。
これはすなわち、波動関数
\(
\displaystyle\psi(x)=\int \psi(x’)\delta(x-x’)dx
\)
を離散化すると、
\(
\begin{align}
\psi(x_i)&=\sum _j \psi(x_j)\frac{\delta_{i,j}}{\Delta x}\cdot \Delta x \\
&=\sum _j \psi(x_j)\delta_{i,j}
\end{align}
\)
と表現できます。ここで、積分を区分求積に変えたため、\(\Delta x\)が掛けられています。
離散化した関数は、
区間\(\displaystyle \left[x_i-\frac{h}{2}, x_i+\frac{h}{2}\right]\)の波動関数\(\psi(x)\)の値を\(\psi(x_i)\)で代表させて近似する
ということです。
※この離散化の考えは自然ですが、非常に非物理的であることに注意してください。なぜならば、\(x_i\pm \frac{h}{2}\)で隣り合う区間の波動関数と、ほとんどの場合不連続になるためです。量子力学では波動関数は滑らかにつながっていなければなりません(カフス等を除いて)。
ハミルトニアンの行列表現
これから考えていく基底関数を用いてハミルトニアンを行列表示します。
ハミルトニアン\(\hat{H}\)は
\(
\begin{align}
\hat{H}=-\frac{1}{2}\frac{d^2}{dx^2}+V(x)
\end{align}
\)
です。
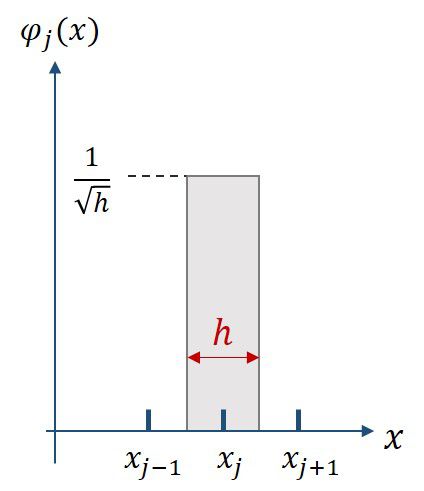
今回用いる基底関数は空間を離散化したもので、数式で表せば、
\(
\begin{eqnarray}
\varphi_i(x)=
\left\{
\begin{aligned}
& \frac{1}{\sqrt{h}} ~~~~~~(x_i-h/2 \lt x \lt x_i+h/2) \\
& \frac{1}{2\sqrt{h}} ~~~~~~(x = x_i\pm h/2) \\
& 0 ~~~~~~(上以外)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。係数の値は正規直交化
\(
\displaystyle \int_{-\infty}^{\infty} \varphi_i(x)\varphi_j(x) dx =\delta_{i,j}
\)
を満たすように決定しています(実関数なので、複素共役は消しています)。
この基底関数は正規直交であるだけでなく、選点直交性と呼ばれる直交性をも持ちます。それは、
\(
\displaystyle \varphi_i(x_j)=\frac{1}{\sqrt{h}}\delta_{i,j}
\)
という直交性です。この性質は積分を計算する際に非常に役立ちます。
波動関数が
\(
\displaystyle \psi(x)=\sum_i c_i \varphi_i(x)
\)
で近似されることを仮定し、変分法の考えに基づいて係数\(c_i\)を求めます。
要素の計算
ハミルトニアン要素を計算していきます。
まず、ポテンシャルの項の方が簡単なのでこちらを計算してしまいます。
\(
\begin{align}
\int_{-\infty}^{\infty} \varphi_i(x)V(x)\varphi_j(x)dx
&=\frac{1}{\sqrt{h}}\int_{x_i-\frac{h}{2}}^{x_i+\frac{h}{2}} V(x)\varphi_j(x)dx \\
&=V(x_i)\delta_{i,j} \\
\end{align}
\)
と書けます。\(i,j\)が同じでなければ、基底関数がゼロになってしまうので値を持ちません。よって上が導けます。簡単ですね。
補足しますと、この基底関数系では任意の関数\(f(x)\)を基底関数で挟んだ値は
\(
\displaystyle \int_{-\infty}^{\infty} \varphi_i(x) f(x)\varphi_j(x) dx \approx f(x_i)\delta_{i,j}
\)
と計算できます。よって、任意の関数\(f(x)\)の系の期待値は
\(
\begin{align}
&\int_{-\infty}^{\infty} \psi(x) f(x)\psi(x) dx \\
&\approx \sum_i \sum_j \int_{-\infty}^{\infty} \varphi_i(x) f(x)\varphi_j(x) dx \\
&=\sum_i \sum_j f(x_i)\delta_{i,j} \\
&=\sum_i f(x_i)
\end{align}
\)
と計算されます。非常に簡単ですね。
では、運動エネルギー項を計算しましょう。
まず一階微分を含む積分は
\(
\begin{align}
\int_{-\infty}^{\infty} \varphi_i(x)\frac{d}{dx}\varphi_j(x)dx
&=\frac{1}{\sqrt{h}}\int_{x_i-\frac{h}{2}}^{x_i+\frac{h}{2}} \frac{d}{dx}\varphi_j(x)dx \\
&=\frac{1}{\sqrt{h}}\int_{\varphi(x_i-\frac{h}{2})}^{\varphi(x_i+\frac{h}{2})} d\varphi_j(x) \\
&=\frac{1}{\sqrt{h}}\left[\varphi_j(x_i+\frac{h}{2})-\varphi_j(x_i-\frac{h}{2})\right] \\
&=\frac{1}{\sqrt{h}}\left[\frac{1}{2\sqrt{h}}\left(\delta_{j,i+1}+\delta_{j,i}-\delta_{j,i-1}-\delta_{j,i}\right)\right] \\
&=\frac{1}{2h}\left(\delta_{j,i+1}-\delta_{j,i-1}\right)
\end{align}
\)
となります。これはまさに中央差分です。二階微分は、
\(\begin{align}
&\int_{-\infty}^{\infty} \varphi_i(x)\frac{d^2}{dx^2}\varphi_j(x)dx \\
&=\frac{1}{\sqrt{h}}\left[\left.\frac{d\varphi_j}{dx}\right|_{x=x_i+h/2}-\left.\frac{d\varphi_j}{dx}\right|_{x=x_i-h/2}\right]\\
&~~~~~~~\left(\frac{d\varphi_j}{dx}=\frac{1}{\sqrt{h}}\left[\delta\left(x-(x_j-h/2)\right)-\delta(x-(x_j+h/2))\right]\mbox{より}\right) \\
&=\frac{1}{h}\left[\delta(x_i+h/2-(x_j-h/2))-\delta(x_i+h/2-(x_j+h/2)\right. \\
&~~~~~~~~~~~~ \left. -\delta(x_i-h/2-(x_j-h/2))+\delta(x_i+h/2-(x_j+h/2))\right] \\
&=\frac{1}{h}\left[\delta(x_i-x_j+h)-2\delta(x_i-x_j)+\delta(x_i-x_j-h)\right] \\
&~~~~~~~\delta(x_i-x_j)\rightarrow\frac{\delta_{i,j}}{h}\mbox{の関係を用いて} \\
&=\frac{1}{h^2}\left[\delta_{j,i+1}-2\delta_{j,i}+\delta_{j,i-1}\right] \\
\end{align}
\)
と計算できます。
最後の式はまさに微分を差分で近似したものと一緒です。
ということは、
微分を上記の差分に置き換えるということは、矩形型の基底関数で展開したものと同じ事が示せました。