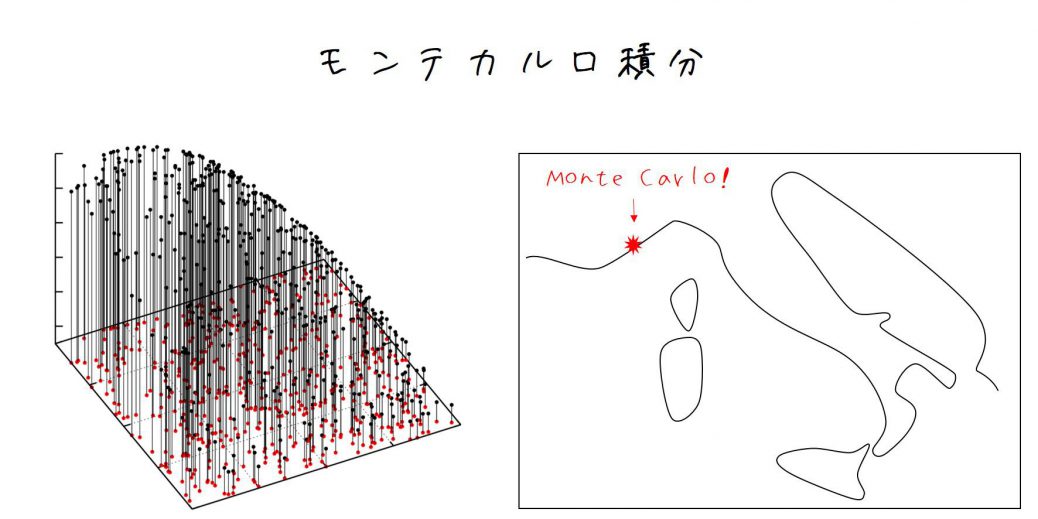
モンテカルロ積分は乱数を利用した積分方法です。

モンテカルロ積分の精度を1桁上げるためには評価点の数を100倍に増やす必要があります。
ですが、この性質は次元数に依らないため、多重積分(5~8次元以上など)を行うときに有利な性質を持ちます。

また、とにかく実装が簡単なので非常に使い易いです。

1次元のモンテカルロ積分

1次元のモンテカルロ積分は定積分を
\(
\displaystyle \int_a^b f(x)dx \approx \frac{1}{N}\sum_{i=1}^N\frac{f(x_i)}{p(x_i)}+O(\frac{1}{\sqrt{N}})
\)
として求めます。
ここで、\(x_i\)は\(p(x)\)に従って\(i\)番目に発生させた乱数で、
\(p(x)\)は区間\([a,b]\)内の乱数の分布を表す関数で、
\(
\displaystyle \int_a^b p(x) dx =1
\)
を満たします。一様乱数であれば
\(
\displaystyle p(x)=\frac{1}{b-a}
\)
です。モンテカルロ積分は一様乱数のみで出来るのではなく、任意の乱数分布に対して適用することが出来ます。

一様乱数によるでD次元の積分は、
\(
\begin{align}
&\int_{x^{(1)}_{a}}^{x^{(1)}_{b}}\int_{x^{(2)}_{a}}^{x^{(2)}_{b}}\cdots\int_{x^{(D)}_{a}}^{x^{(D)}_{b}}
f(x^{(1)},x^{(2)},\cdots,x^{(D)})dx^{(D)}\cdots dx^{(2)} dx^{(1)} \\
&\hspace{1em}\approx
\frac{(x^{(1)}_{b}-x^{(1)}_{a})(x^{(2)}_{b}-x^{(2)}_{a})\cdots(x^{(D)}_{b}-x^{(D)}_{a})}{N}
\sum_{i=1}^N f(x^{(1)}_i,x^{(2)}_i,\cdots,x^{(D)}_i)
+O(\frac{1}{\sqrt{N}})
\end{align}
\)
と求める事が出来ます。

モンテカルロ積分の誤差はサンプル数にのみに依存します。
モンテカルロ積分の誤差は\(O(\frac{1}{\sqrt{N}})\)なので、サンプル数\(N\)を100倍に増やすと積分精度が\(\frac{1}{\sqrt{100}}=\frac{1}{10}\)、つまり1桁上がる事を意味しています。

一般的な数値積分法、例えば台形則を用いて1次元積分を\(N\)点で積分するとします。
すると、2次元の積分では\(N^2\)点、D次元では\(N^D\)点被積分関数を評価する必要があります。
台形則を組み合わせて積分する場合、精度は\(N\cdot O(h^2)\sim O(\frac{1}{N})\)で決まるので、
1桁、積分精度を上げたいとすれば被積分関数の評価回数は\(10^{D}\)倍に増やさなければなりません。

しかしモンテカルロ積分では積分の精度は次元に依らずサンプル数にのみで決定されます。これは、
1桁、積分精度を上げたいとすれば被積分関数の評価回数は\(100\)倍に増やさなければならないことを意味しています。

台形則と比べると収束速度は、おおよそ3重積分を解こうとする際に、モンテカルロ法の方が有利になる、ということが分かります。

(注意)
3次元の定積分を考えます。
この時、台形則では100点で真値と1桁、モンテカルロ積分では10000点で真値と2桁合っているとします。
この状態から精度を1桁上げようとすると関数の評価回数は
台形 \(100\times 10^3= 100,000 \)点
モンテカルロ積分 \(10000\times 100\approx 1,000,000\)点
となり、この場合では台形の方が評価回数が少なくて済みます。ずっと繰り返せばモンテカルロ積分の方が少なくなりますが、現実的な評価回数ではなくなると思います。
なので、評価回数が増えていく割合が変わるのは3重積分あたりですが、最終的に評価回数が少なくなるのはもっと多次元の積分を実行する時かもしれません。

台形則と比較しましたが、台形則の代わりにガウス求積法を用いた場合、もう少し高次元で逆転します。

実用的には6~10次元以上でモンテカルロ積分が使われるようです。

乱数について

モンテカルロ積分は乱数を利用して積分を行うため、乱数の性質が重要になってきます。
私は乱数について詳しくありませんが、調べた限りメルセンヌツイスタという乱数発生法が良い乱数を発生するようです。
メルセンヌツイスタの詳細はMersenne Twister Home Page にあるのでご参照ください。
fortran90コードはhttps://gist.github.com/ykonishi/5569005にあります。

fortran90コード

1次元の積分
\(
\displaystyle \int_0^2 \sin x dx \approx 1.416146836547142\cdots
\)
を実際にメルセンヌツイスタを用いて、計算します。
関数の評価点数は10000点です。

下のコードを実行すると

という出力を得ます。１列目が関数の評価数、2列目がモンテカルロ積分による積分値、3列目が真値です。
1万点の評価で、ただのsin関数を計算しているのに4桁程度というのは経験的に非常に良くない精度です。
しかも、乱数を用いているので、4桁一致していると判断するのは危険です。
もっと乱数を発生させて、値が変わらないのかチェックを欠かすことはできません。

モンテカルロ積分は以下のプログラムで可能です。

コンパイルは上のファイルをmain.f90と名付けた場合

とします。もしもエラーが出てしまう場合

とします。
このエラーはgfortranコンパイラ(ver4.8.4で確認)の問題です。
fortranの整数は
-2147483648から2147483647までで定義されているのにもかかわらず、
gfortran(ver4.8.4)は
-2147483647から2147483647の範囲でなければエラーを出すようです。
しかし、実際に整数に-2147483648を代入し、このエラーを無視する上のオプションを付けて実行すると、ちゃんと値が入ります。なので、コンパイラに問題があると判断しました。

3次元積分

3次元の定積分を2つ考えます。
\(
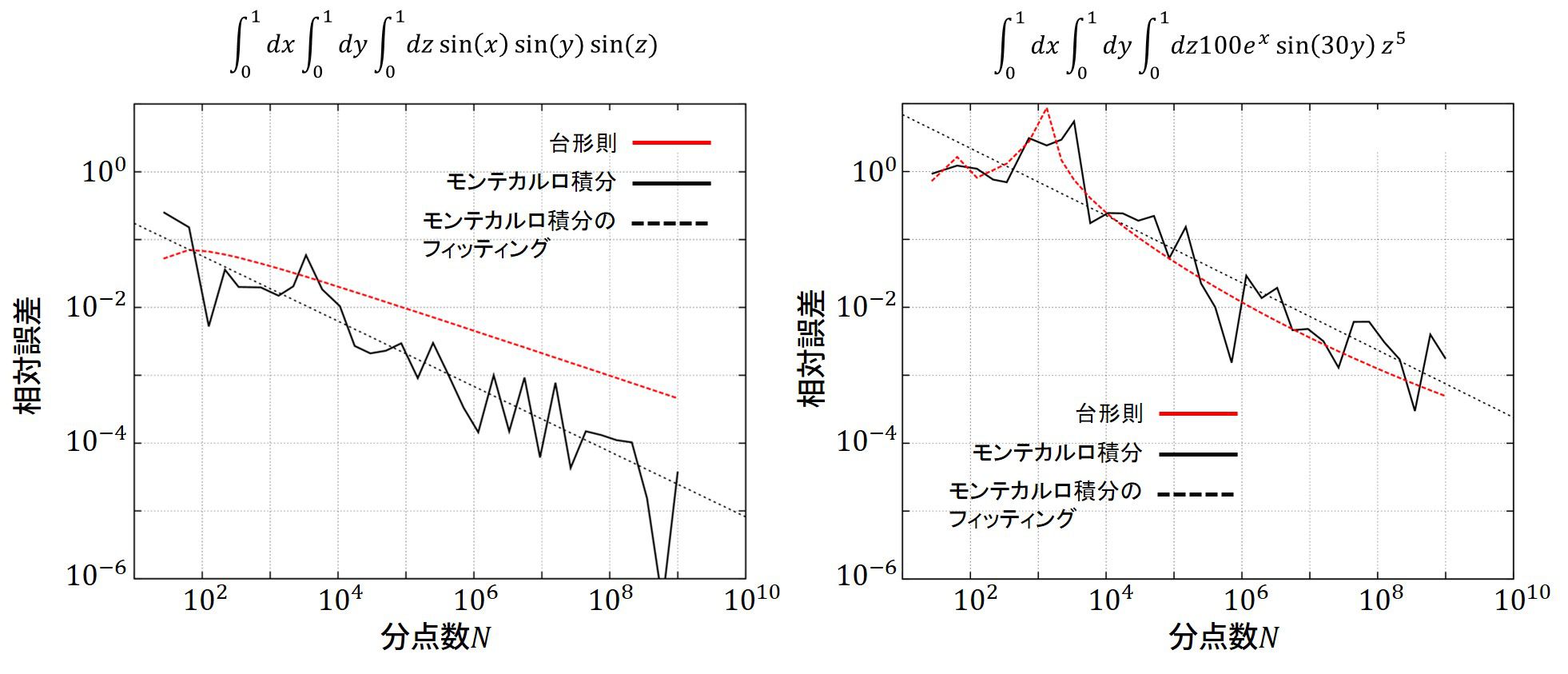
\displaystyle \int_0^1 dz \int_0^1 dy \int_0^1 dx \sin(x)\sin(y)\sin(z) \approx 0.097144222323873819\cdots
\)
\(
\displaystyle \int_0^1 dz \int_0^1 dy \int_0^1 dx 100 e^{x}\sin(30y)z^5 \approx 0.80735242505763782\cdots
\)

比較する積分法はモンテカルロ積分、台形則、quadpackによる自動積分です。
quadpackは15-31点ガウス求積法を用います。3次元関数のfortranによるquadpackコードはこちら

結果は以下の図の方になりました。

quadpackについては余りにも精度が違い過ぎるので図には重ねていません。
それぞれ、関数の評価回数と積分値を載せました。下線は真値と一致している桁です。

quadpack, key=3
3375points, 0.097 144 222 323 873 861
50625points,0.807 352 425 057 637 71

左の図で、台形則では一次元方向の分点数が10倍(3次元なのでグラフ上では1000倍)になると積分の精度が約1桁上昇し、モンテカルロ積分では点数が100倍増えると積分の精度が約1桁上昇しているのが見て取れます。
右の図ではあたかも台形則の方が傾きが急峻そうに見えますが、まだ安定している積分になってなく、傾きが緩やかになっていきそうなことが分かります。

QUADPACKは流石と言いますが、次元が増えると辛いですがまだまだモンテカルロ積分を使わなくてよさそうです。関数の評価点数が5桁なのにほぼ全桁一致しています。

用いたメインのプログラムは以下のものです。これと上で紹介した
メルセンヌツイスタのfortran90プログラム,3次元quadpackプログラムを一緒にコンパイルしてください。

参考文献

モンテカルロ法 (Monte Carlo method)
確率密度関数からモンテカルロ積分まで
メルセンヌツイスタMersenne Twister Home Page
メルセンヌツイスタのfortran90コードhttps://gist.github.com/ykonishi/5569005

Tweet