\(e^{i{\bf k\cdot r}}\)が\({\bf k}\)の方向に進行すること、\(e^{-i{\bf k\cdot r}}\)が\(-{\bf k}\)の方向に進行することの所以を証明します。
まとめ
波は、実部と虚部を並べた時、虚部がある方向に進行していきます。
証明
一次元自由粒子の時間発展を考えます。
自由粒子の時間依存シュレーディンガー方程式は
\(
\displaystyle i\hbar\frac{\partial}{\partial t}\Psi(x,t)=\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\right)\Psi(x,t)
\)
と書けます。時間依存しないシュレーディンガー方程式を求めるために、
\(\Psi(x,t)=\psi(x)e^{-i\frac{E}{\hbar}t}\)
と置いて代入すると
\(
\displaystyle -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi(x)=E\psi(x)
\)
となります。
上の微分方程式の解は、
\(
\psi(x)=e^{\pm i{\sqrt{\frac{2mE}{\hbar^2}}x}}
\)
です。通常、波数\(k=\sqrt{\frac{2mE}{\hbar^2}}\)を定義して、
\(
\psi(x)=e^{\pm ikx}
\)
と書きます。連続状態を考えているので、エネルギー\(E\)は、
\(
\displaystyle E=\frac{\hbar^2k^2}{2m}
\)
です。
時間依存しないシュレーディンガー方程式が解けたので、時間依存するシュレーディンガー方程式の解\(\Psi(x,t)\)は、角周波数\(\omega=\frac{E}{\hbar}\)を用いて、
\(
\begin{align}
\Psi(x,t)&=e^{\pm ikx}e^{-i\frac{E}{\hbar}t} \\
&=e^{i(\pm kx-\omega t)}
\end{align}
\)
と記述されます。
\(e^{ikx}\)の解について
時間依存しない解が
\(e^{ikx}\)
に対する時間発展を考えます。
この時、時間依存する解は\(e^{i(kx-\omega t)}\)ですが、変形して、
\(
\displaystyle e^{ik(x-\frac{\omega}{k} t)}
\)
と書きます。
時刻\(t=0\)に対して、波動関数は\(e^{ikx}\)
時刻\(t=\Delta t\)に対して、波動関数は\(e^{ik(x-\frac{\omega}{k}\Delta t)}\)
です。よって、時刻\(t=0\to \Delta t\)の間に、関数が\(f(x)\to f(x-a)\)になった、つまり位置\(+a\)だけ平行移動された関数になった、とみることができます。
なので進行する波であると言えるのです。
また、その時の進行速度を考えますと、時間\(\Delta t\)の間に距離\(\frac{\omega}{k}\Delta t\)だけ進んだわけですから、速度\(v\)は、
\(
\displaystyle v=\frac{\frac{\omega}{k}\Delta t}{\Delta t}=\frac{\omega}{k}
\)
です。
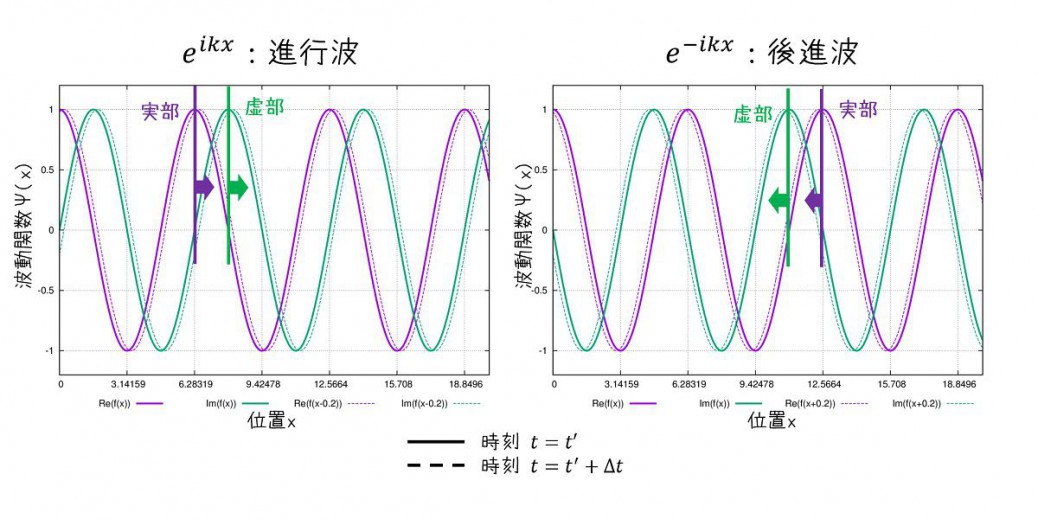
グラフで時間経過を表せば、以下のようになります。
時刻t=0で\(e^{ikx}\)で表される波形(実線、実部:紫線、虚部:緑線)が時間経過して\(e^{ik(x-\frac{\omega}{k}\Delta t)}\)となると破線になります。
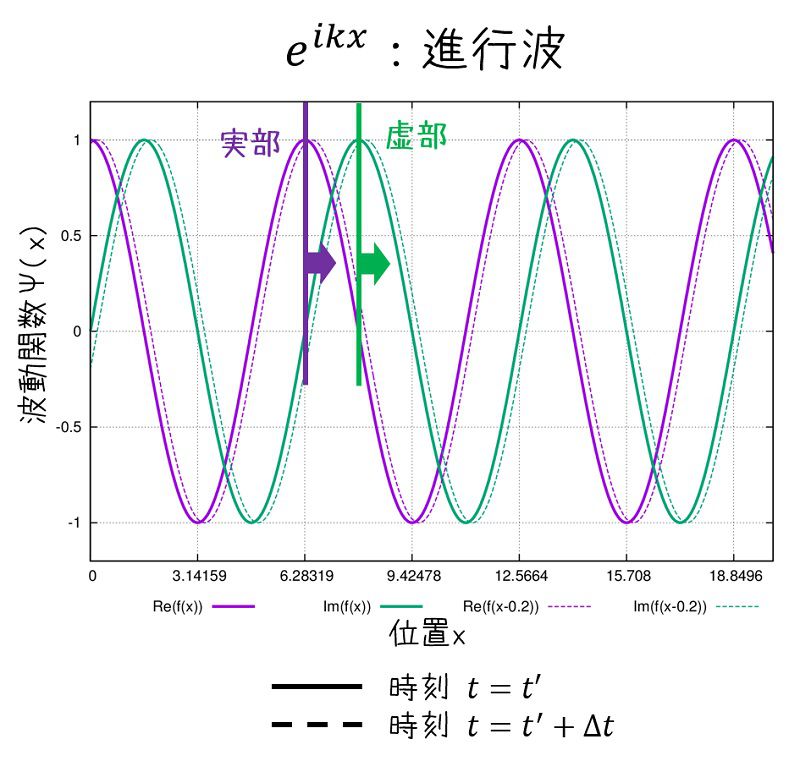
↑画像のgnuplotスクリプト
\(e^{-ikx}\)の解について
次に時間依存しない解が
\(e^{-ikx}\)
に対する時間発展を考えます。
この時、時間依存する解は\(e^{-i(kx+\omega t)}\)ですが、変形して、
\(
\displaystyle e^{-ik(x+\frac{\omega}{k} t)}
\)
と書きます。
時刻\(t=0\)に対して、波動関数は\(e^{-ikx}\)
時刻\(t=\Delta t\)に対して、波動関数は\(e^{-ik(x+\frac{\omega}{k}\Delta t)}\)
です。よって、時刻\(t=0\to \Delta t\)の間に、関数が\(f(x)\to f(x+a)\)になった、つまり位置\(-a\)だけ平行移動された関数になった、とみることができます。
なので後進する波であると言えるのです。
また、その時の進行速度を考えますと、時間\(\Delta t\)の間に距離\(-\frac{\omega}{k}\Delta t\)だけ進んだわけですから、速度\(v\)は、
\(
\displaystyle v=\frac{-\frac{\omega}{k}\Delta t}{\Delta t}=-\frac{\omega}{k}
\)
です。
グラフで時間経過を表せば、以下のようになります。
時刻t=0で\(e^{-ikx}\)で表される波形(実線、実部:紫線、虚部:緑線)が時間経過して\(e^{-ik(x+\frac{\omega}{k}\Delta t)}\)となると破線になります。
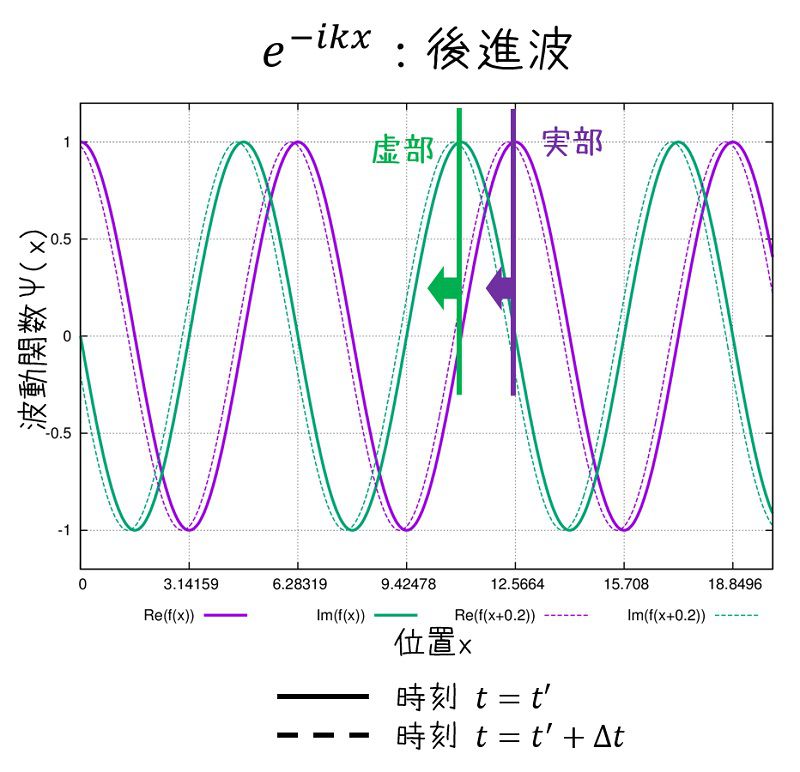
↑画像のgnuplotスクリプト
波動関数は、
進行する波は虚部が先に来て後から実部(実部の位相が\(\pi/2\)遅れる)
後進する波は実部が先に来て後から虚部(虚部の位相が\(\pi/2\)遅れる)
のように見えます。
言い換えれば、波は虚部が先行している方向に進む、ということです。
3次元の場合
3次元でも同じことが言えます。
3次元自由粒子のハミルトニアンは
\(
\displaystyle \hat{H}=-\frac{\hbar^2}{2m}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)
\)
で変数分離可能なので、3次元の1つの方程式ではなく、1次元の3つの方程式に変換可能であり、x,y,z方向は独立に決められます。
なので、
\(
\displaystyle \Psi(x,y,z,t)=e^{ik_x(x-\frac{\omega_x}{k_x} t)+ik_y(y-\frac{\omega_y}{k_y} t)+ik_z(z-\frac{\omega_z}{k_z} t)}
\)
と表されます。
ここで\(\omega_x, \omega_y, \omega_z\)は、1次元の3つの方程式に分けた時のそれぞれのエネルギー固有値\(E_x,E_y,E_z\)に対応する角周波数を示しています(\(\omega_i=E_i/\hbar,\;\; (i=x,y,z)\))。(エネルギーは\(E=E_x+E_y+E_z\)です。)
上の場合は\({\bf k}=(k_x,k_y,k_z)\)方向に進行する波を表します。
通常は波数ベクトルとして書いて、
\(
\begin{align}
& \Psi({\bf r},t)= e^{i{\bf k \cdot r}-\omega t} \\
&\;\;\;\;\; {\small (\omega=\omega_x+\omega_y+\omega_z)}
\end{align}
\)
と書かれます。