正多角形とスピログラフの数式です。
- 正多角形(2次元)
- 正多角形(3次元)
- 星型多角形(2次元)
- 星型多角形(3次元)
- トロコイド(2次元)
- トロコイド(3次元)
- スピログラフ
2016/10/24
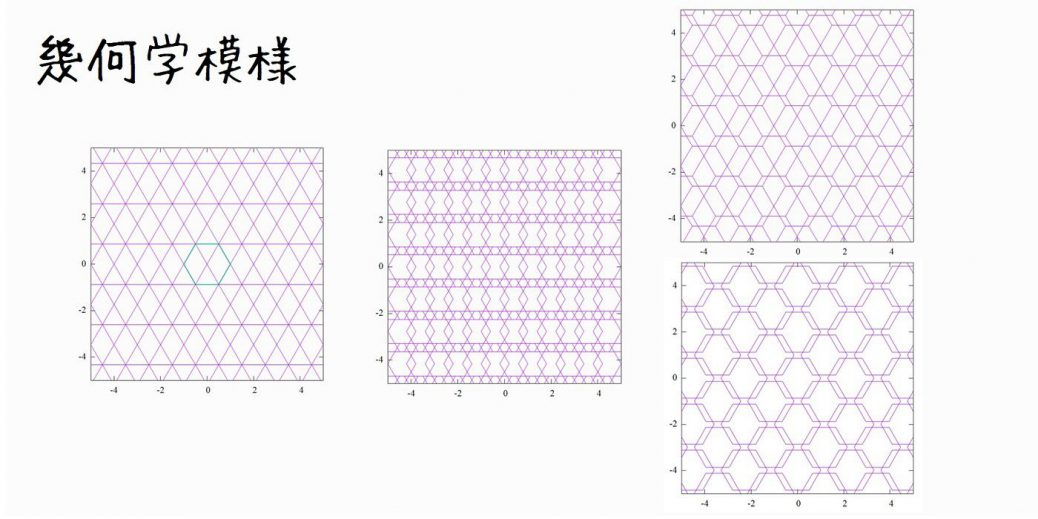
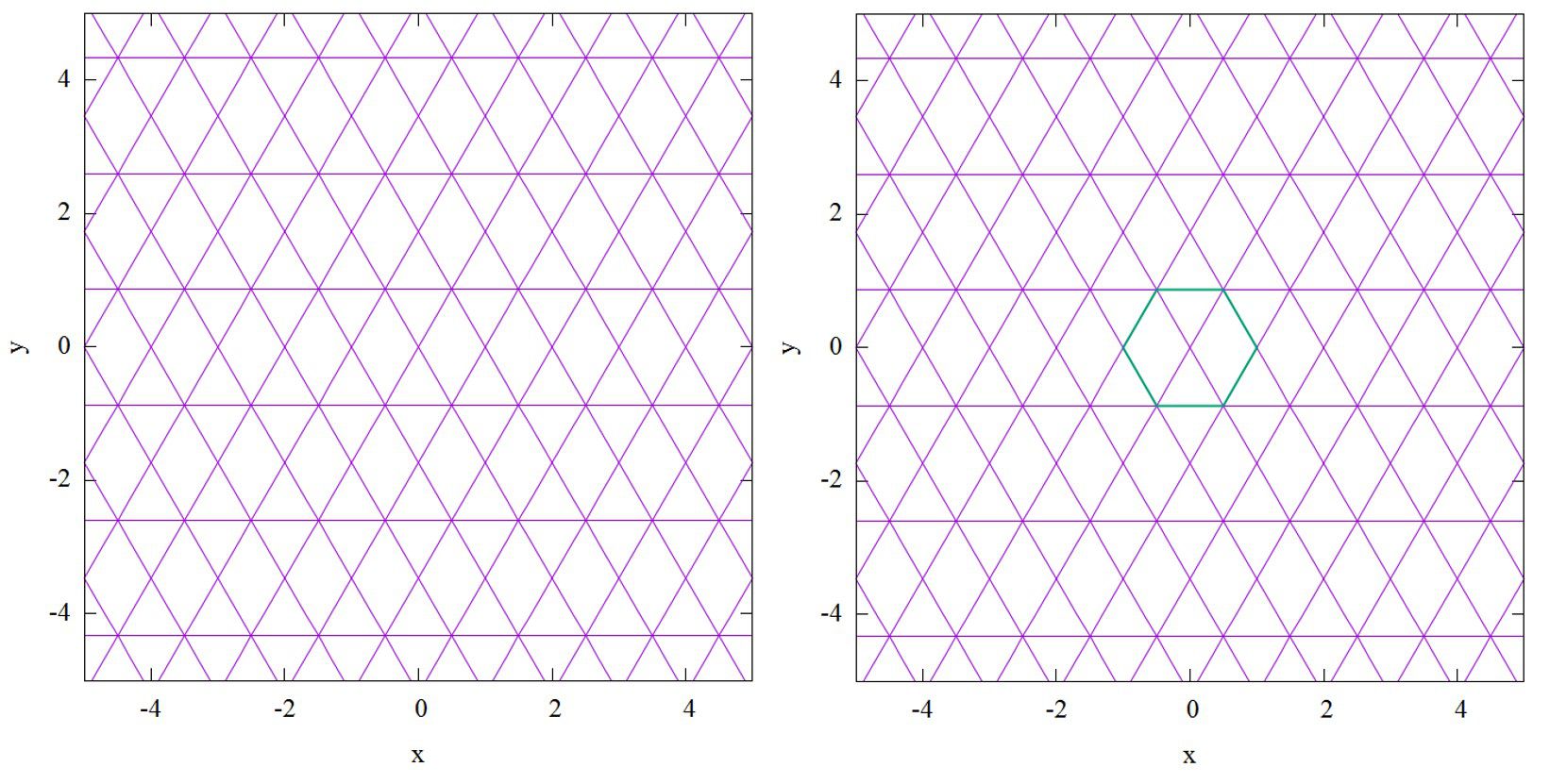
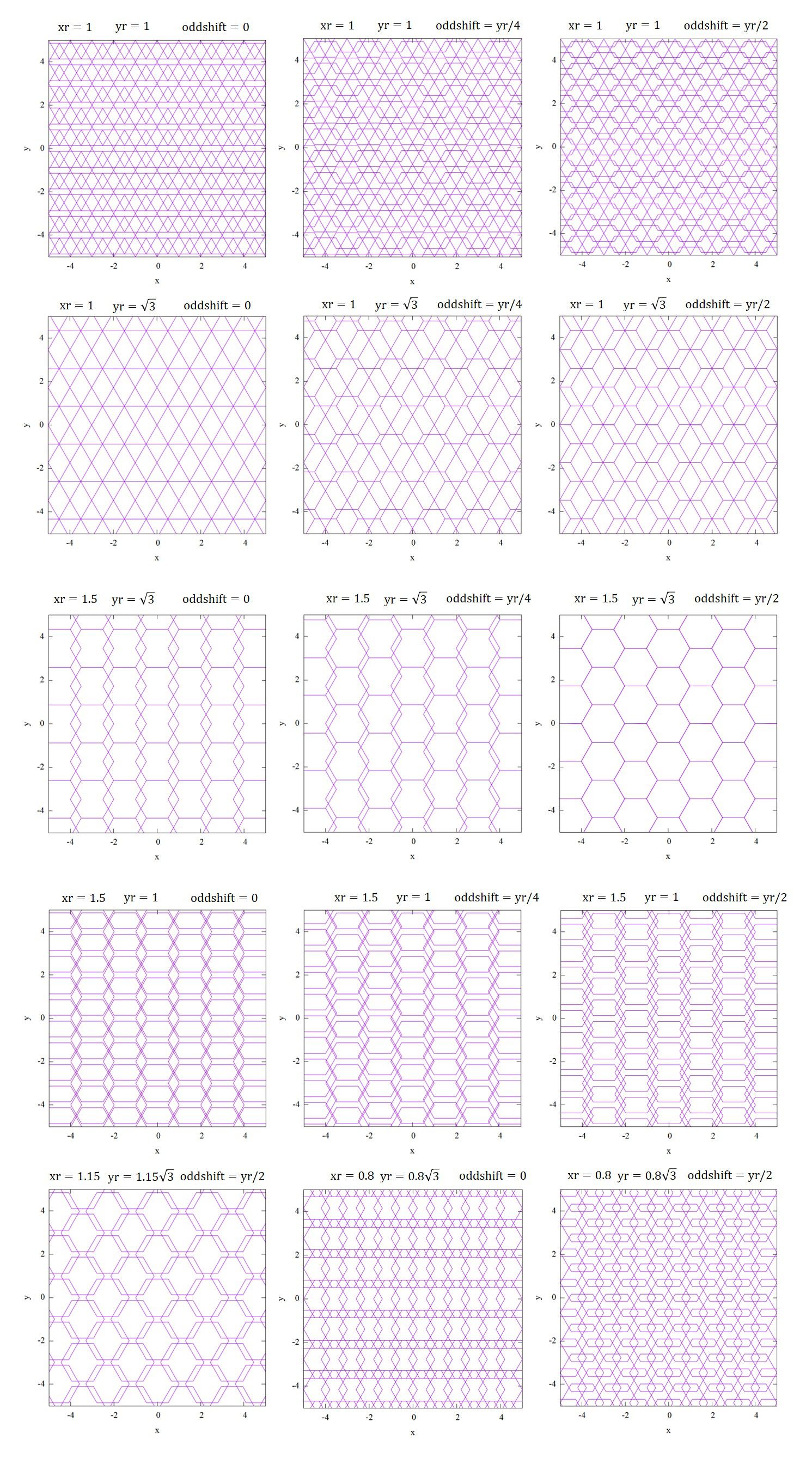
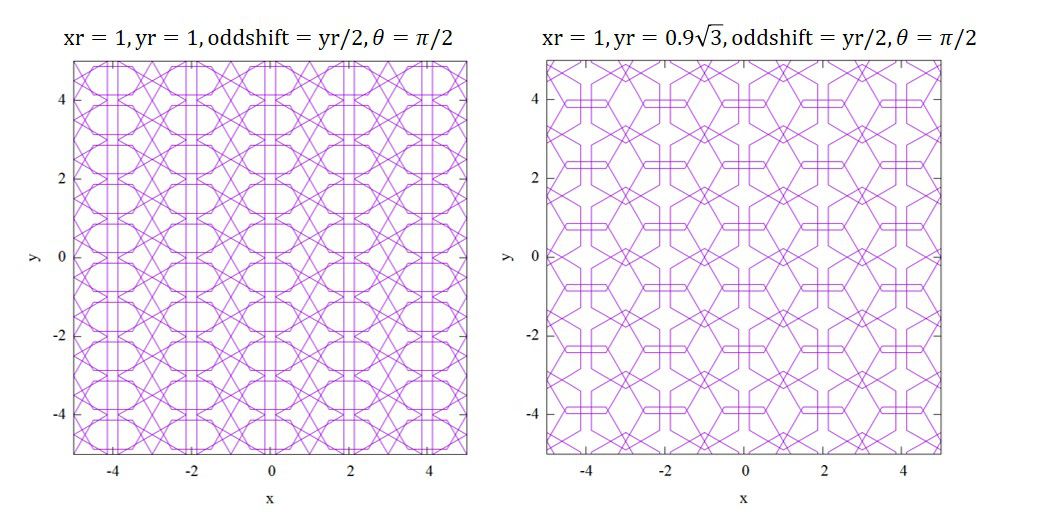
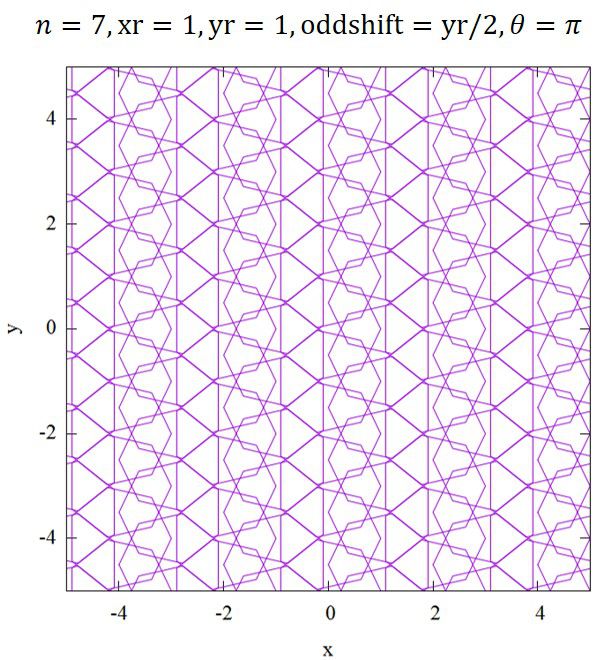
幾何学模様を作りたい方は幾何学模様(gnuplot)へどうぞ。
[adsense1]
正多角形の式(2次元)
正n角形の数式は[1]を参考に修正しました。
正n角形の数式は、
\(
\begin{equation}
\left\{
\begin{aligned}
x&\displaystyle =\cos t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}\\
y&\displaystyle =\sin t \cdot \frac{\cos \frac{a_n}{2}}{\cos\left[a_n\left\{\frac{t}{a_n}-{\rm floor}\left(\frac{t}{a_n}\right)\right\}-\frac{a_n}{2}\right]}
\end{aligned}
\right.
\end{equation}
\)
です。ここで、\(a_n=\frac{2\pi}{n}\)と置きました。また、\({\rm floor}(x)\)は床関数(床関数と天井関数)を表します。
媒介変数\(t\)の範囲は(\(0\le t \lt 2\pi\))です。
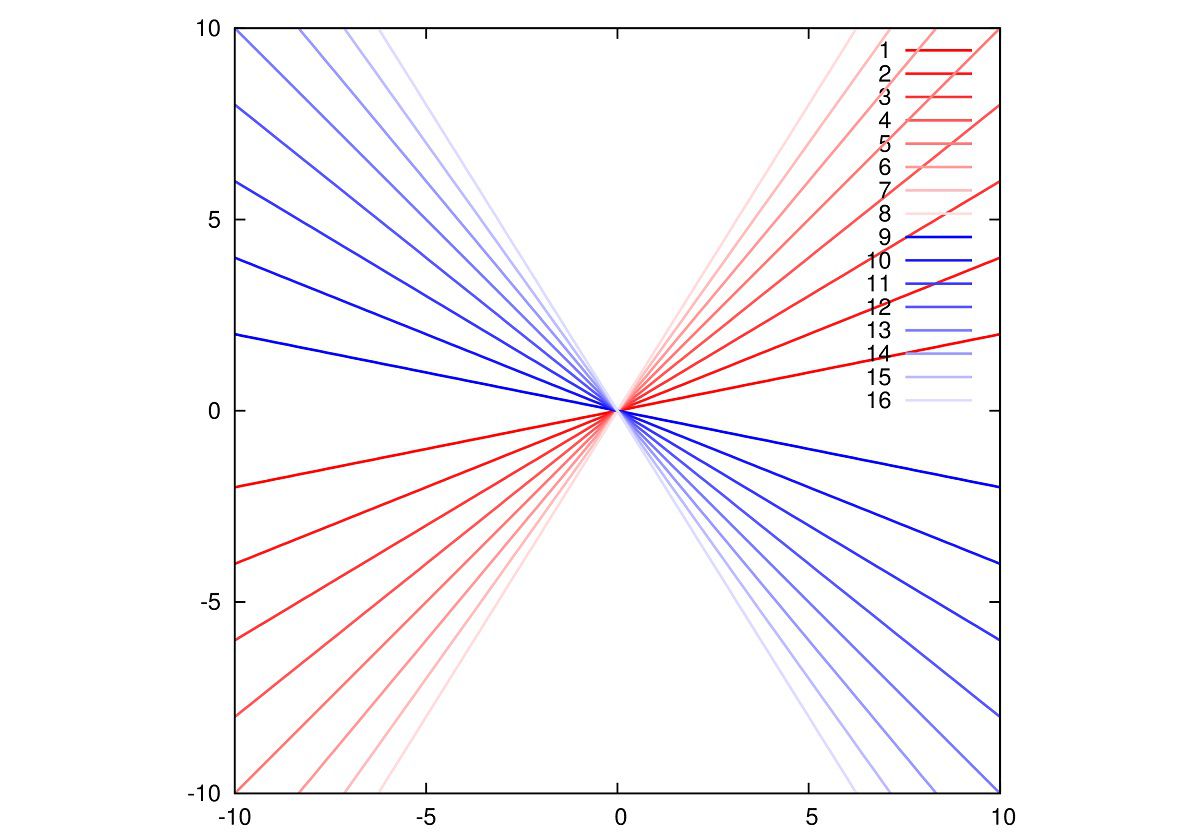
グラフを書かせてみますとこうなります。
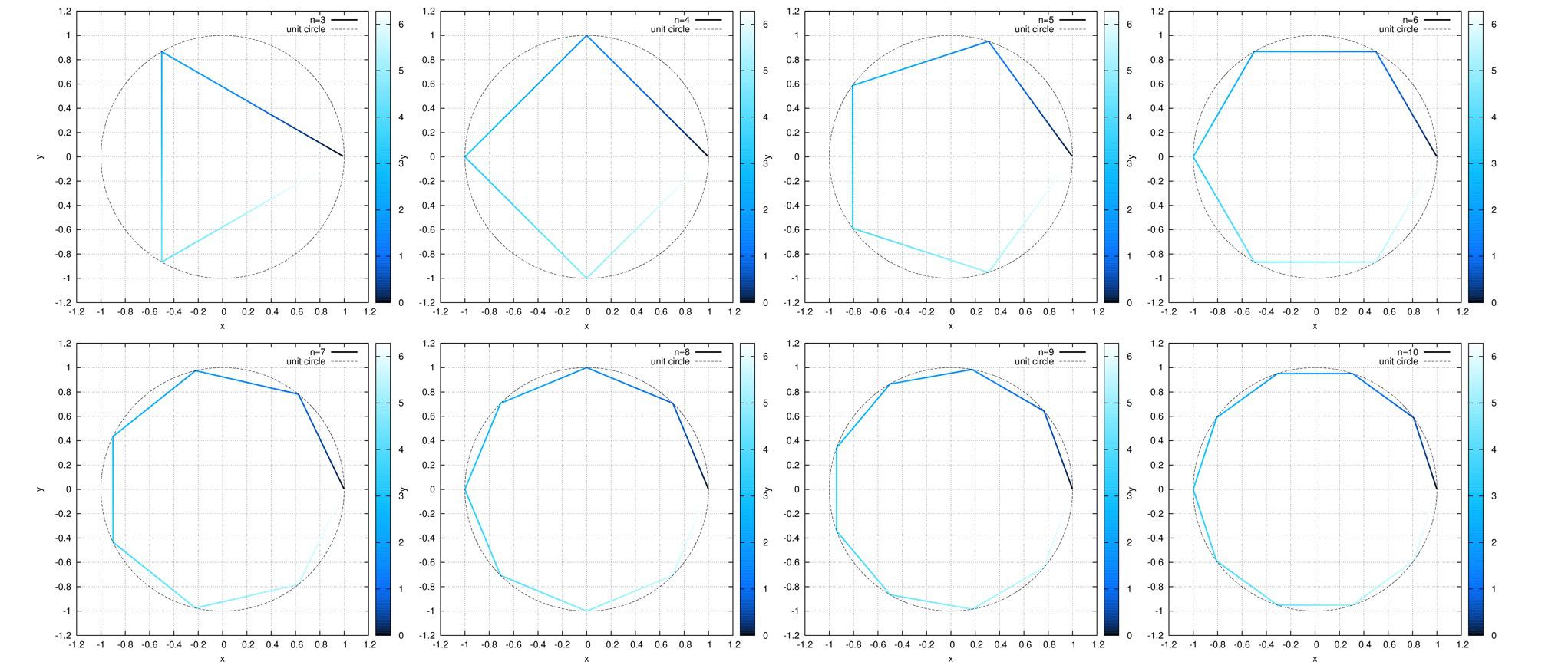
n=3,4,5,6
n=7,8,9,10の順で、単位円を一緒に記述しています。
線の色の濃さは媒介変数の値に応じて変化させています。
gnuplotのスクリプトはこちら
set param
set size squ
set grid
set xr[-1.2:1.2]
set yr[-1.2:1.2]
set tr[0:2*pi]
set cbr[0:2*pi]
set xtics 0.2
set ytics 0.2
set xl "x"
set yl "y"
set palette cubehelix start 2.7 cycles 0 saturation 4
# +---polygon---+
s1(x)=x-floor(x)
a(n)=2e0*pi/real(n)
cnp(n,t)=cos(a(n)*s1(t/a(n))-0.5e0*a(n))
pc(n,t)=cos(t)*cos(0.5e0*a(n))/cnp(n,t)
ps(n,t)=sin(t)*cos(0.5e0*a(n))/cnp(n,t)
set samples n*50+1
plot pc(n,t),ps(n,t) lw 3 ti sprintf("n=%d",n)
#l set table "d1.d"
#l plot t,cos(0.5e0*a(n))/cnp(n,t)
#l unset table
#l
#l set table "d2.d"
#l splot "d1.d" u (cos($1)*$2):(sin($1)*$2):($1)
#l unset table
#l
#l plot "d2.d" u 1:2:3 w l lw 4 lc palette ti sprintf("n=%d",n), cos(t),sin(t) lc 8 ti "unit circle"
最後のコメントアウトを外すと、線の色を媒介変数に応じた色付けにできます。
多面体の式(3次元)
半径1の多面体は、平面のx,yの媒介変数による正n角形の関数をそれぞれpc(t),ps(t)と置くと、
\(
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm ps}(u)\cdot {\rm pc}(v) \\
y& = {\rm ps}(u)\cdot {\rm ps}(v) \\
z& = {\rm pc}(u)
\end{aligned}
\right.
\end{equation}
\)
と書けます。
媒介変数\(u,v\)の範囲は(\(0\le u \lt \pi, \;\; 0\le v \lt 2\pi\))です。
プロットすると以下のようになります。
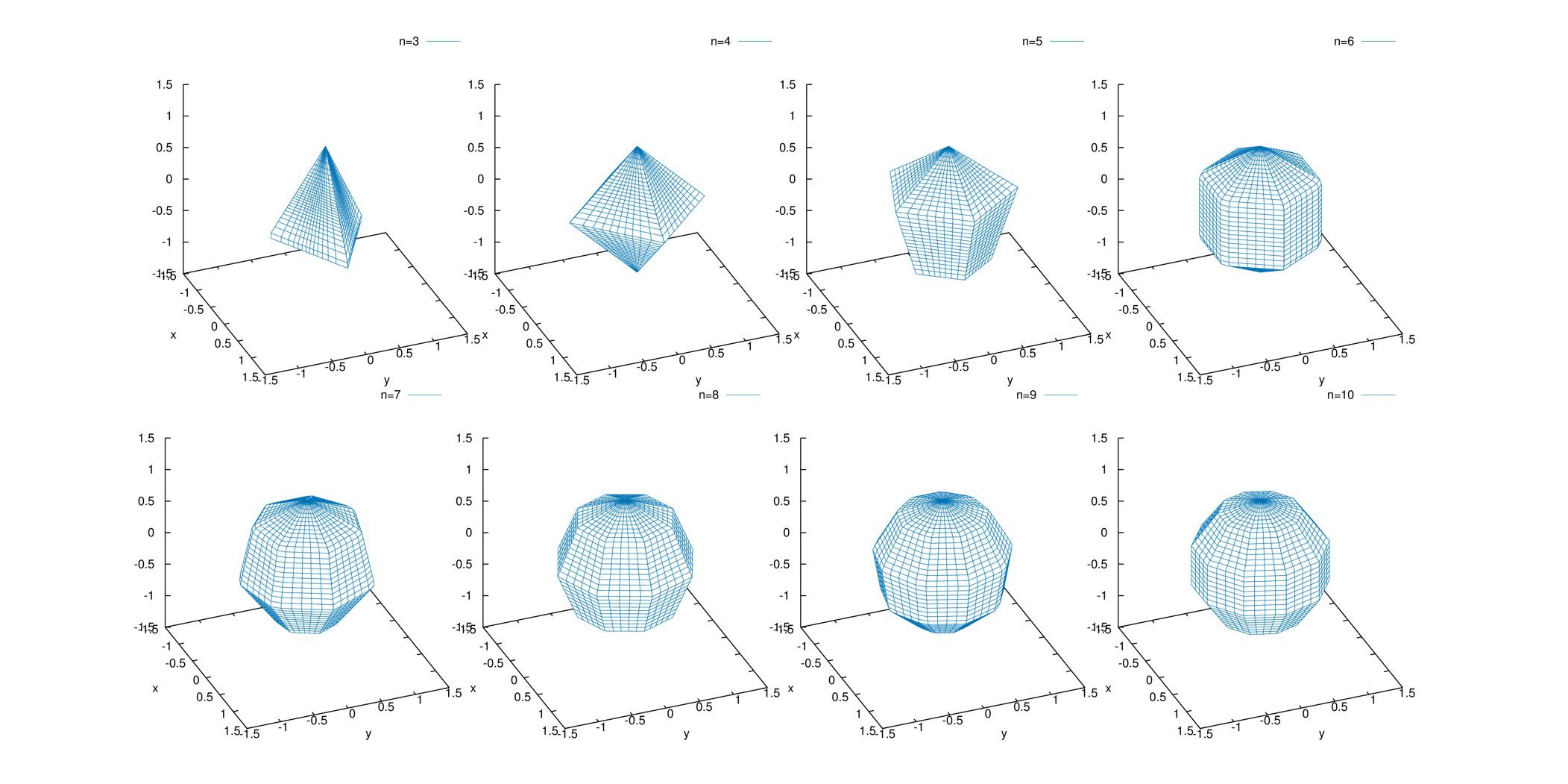
n=3,4,5,6
n=7,8,9,10の順です。
gnuplotスクリプトはこちら
set param
set hidden3d
set ticslevel 0
set xr[-1.5:1.5]
set yr[-1.5:1.5]
set zr[-1.5:1.5]
set view equal xyz
set view 60,68,1,1
set ur[0:pi] # theta
set vr[0:2*pi] # phi
set xl "x"
set yl "y"
# +---polygon3d---+
s1(x)=x-floor(x)
a(n)=2e0*pi/real(n)
cnp(n,t)=cos(a(n)*s1(t/a(n))-0.5e0*a(n))
pc(n,t)=cos(t)*cos(0.5e0*a(n))/cnp(n,t)
ps(n,t)=sin(t)*cos(0.5e0*a(n))/cnp(n,t)
p3x(n,u,v)=ps(n,u)*pc(n,v)
p3y(n,u,v)=ps(n,u)*ps(n,v)
p3z(n,u)=pc(n,u)
set isosamples 41
n=3
splot p3x(n,u,v),p3y(n,u,v),p3z(n,u) lc 6 ti sprintf("n=%d",n)
# # output file
# fn=sprintf("polygon3d_n%d",n)
# print fn
#
# set terminal postscript eps dashed enhanced color
# set output fn.".eps"
# replot
# set out
# set terminal wxt enhanced
# cv=sprintf("convert -density 400x400 %s.eps %s.png",fn,fn)
#
# system cv
星型多角形(2次元)
\(
\begin{equation}
\left\{
\begin{aligned}
x&\displaystyle =\cos t \cdot \frac{\cos a_n}{\cos\left[a_n -\frac{1}{n}\cos^{-1}\{\cos(nt)\}\right]}\\
y&\displaystyle =\sin t \cdot \frac{\cos a_n}{\cos\left[a_n -\frac{1}{n}\cos^{-1}\{\cos(nt)\}\right]}
\end{aligned}
\right.
\end{equation}
\)
です(\(n\ge 5\))。ここで、\(a_n=\frac{2\pi}{n}\)と置きました。
グラフを書かせてみるとこのようになります。
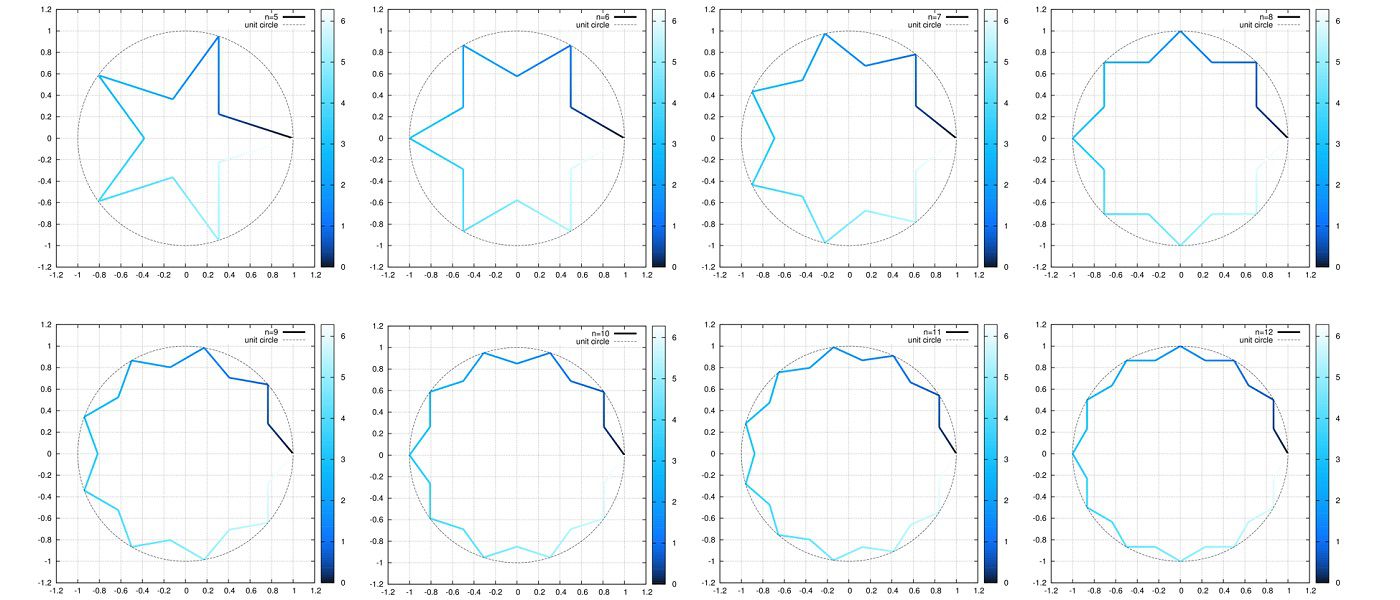
gnuplotスクリプトはこちら。
※\(\cos^{-1}(\cos(x))\)は不安定です。
場合により書けなくなることがあります。ここでは上記関数の代わりに、正弦波ではない周期関数の数式
で記述した関数\(s(a,x)\)を用いています。
set terminal wxt solid noraise enhanced
set param
set tr[0:2*pi]
set cbr[0:2*pi]
set key
set palette cubehelix start 2.7 cycles 0 saturation 4
fl(x)=0.5e0*(floor(x)-floor(-x)-1e0)
s2(x)=x+floor(-x)+1e0
k(a,b,x)=fl((x+a)/(a+b))-fl(x/(a+b))
kk(a,b,x)=2e0*(k(a,b,x)-0.5e0)
s(a,x)=2e0*abs(s2(x/(a*2))-0.5e0)*kk(a*2e0,a*2e0,x+a)
acc(x)=0.5e0*pi*(s(0.5e0*pi,x)+1e0) # equal to acos(cos(x))
a(n)=2e0*pi/real(n)
cns(n,t)=cos(a(n))/cos(a(n)-acc(real(n)*(t))/real(n))
stpc(n,t)=cos(t)*cns(n,t) # star polygon x
stps(n,t)=sin(t)*cns(n,t) # star polygon y
n=5
plot stpc(n,t),stps(n,t) lw 3
#set table "d1.d"
#plot t,cns(n,t)
#unset table
#set table "d2.d"
#splot "d1.d" u (cos($1)*$2):(sin($1)*$2):($1)
#unset table
#plot "d2.d" u 1:2:3 w l lw 6 lc palette ti sprintf("n=%d",n), cos(t),sin(t) lc 8 ti "unit circle"
星型多角形(3次元)
3次元の場合は多面体の時と同じように、平面のx,yの媒介変数による星型多角形の関数をそれぞれstpc(t),stps(t)と置くと、
\(
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm stps}(u)\cdot {\rm stpc}(v) \\
y& = {\rm stps}(u)\cdot {\rm stps}(v) \\
z& = {\rm stpc}(u)
\end{aligned}
\right.
\end{equation}
\)
と書けます。
媒介変数\(u,v\)の範囲は(\(0\le u \lt \pi, \;\; 0\le v \lt 2\pi\))です。
グラフはこのようになります。
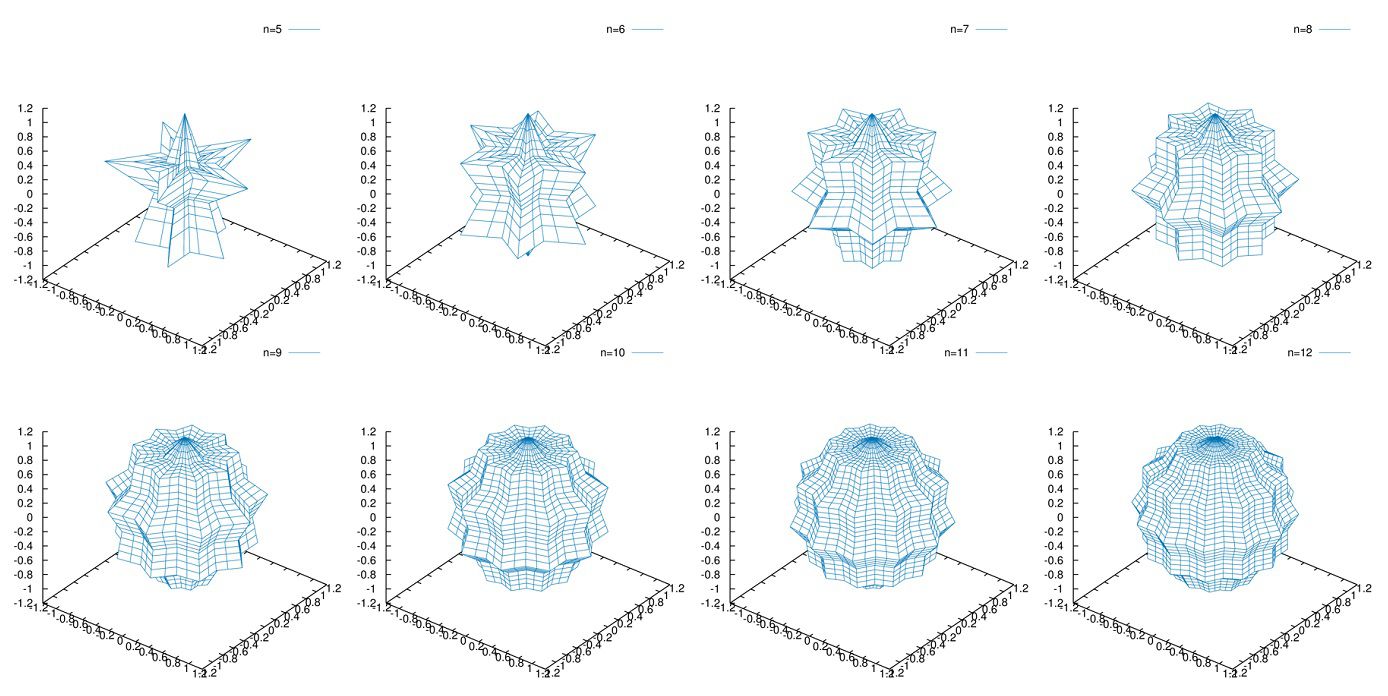
gnuplotスクリプトはこちら。
set terminal wxt solid noraise enhanced
set param
set ticslevel 0
set hidden3d
set view equal xyz
set xr[-1.2:1.2]
set yr[-1.2:1.2]
set zr[-1.2:1.2]
set tr[0:2*pi]
set ur[0:pi]
set vr[0:2*pi]
set cbr[0:2*pi]
set xtics 0.2
set ytics 0.2
set ztics 0.2
set key
set palette cubehelix start 2.7 cycles 0 saturation 4
fl(x)=0.5e0*(floor(x)-floor(-x)-1e0)
s2(x)=x+floor(-x)+1e0
k(a,b,x)=fl((x+a)/(a+b))-fl(x/(a+b))
kk(a,b,x)=2e0*(k(a,b,x)-0.5e0)
s(a,x)=2e0*abs(s2(x/(a*2))-0.5e0)*kk(a*2e0,a*2e0,x+a)
acc(x)=0.5e0*pi*(s(0.5e0*pi,x)+1e0) # equal to acos(cos(x))
a(n)=2e0*pi/real(n)
cns(n,t)=cos(a(n))/cos(a(n)-acc(real(n)*(t))/real(n))
stpc(n,t)=cos(t)*cns(n,t) # star polygon x
stps(n,t)=sin(t)*cns(n,t) # star polygon y
st3x(n,u,v)=stps(n,u)*stpc(n,v)
st3y(n,u,v)=stps(n,u)*stps(n,v)
st3z(n,u)=stpc(n,u)
n=5
set isosamples 21+(4*(n-5))
splot st3x(n,u,v),st3y(n,u,v),st3z(n,u) lw 3
# output file
# fn=sprintf("starpoly3d_n%d",n)
# print fn
#
# set terminal postscript eps dashed enhanced color
# set output fn.".eps"
# replot
# set out
# set terminal wxt enhanced
# cv=sprintf("convert -density 400x400 %s.eps %s.png",fn,fn)
#
# system cv
トロコイド(2次元)
トロコイドと呼ばれる曲線があります[2]。
これをgnuplotで書いてみましょう。数式は[2]を参考にして以下の通りです。
\(
\begin{equation}
\left\{
\begin{aligned}
x& = \left[(n-1)\cos t +h\cos((n-1)t)\right]/n \\
y& = \left[(n-1)\sin t +h\sin((n-1)t)\right]/n
\end{aligned}
\right.
\end{equation}
\)
\(h=1\)の時、半径が1の円に内接するように決めています。
また、\(n\)が整数の時、内接する円が外側の円をちょうど一周回った時に元の位置に戻る条件です。
別に整数でなくても構いません。その時はもっと複雑なものになることでしょう。
書いてみますと曲線はこうなります。
自由度\(h\)を1にしてグラフを書いてみましょう。
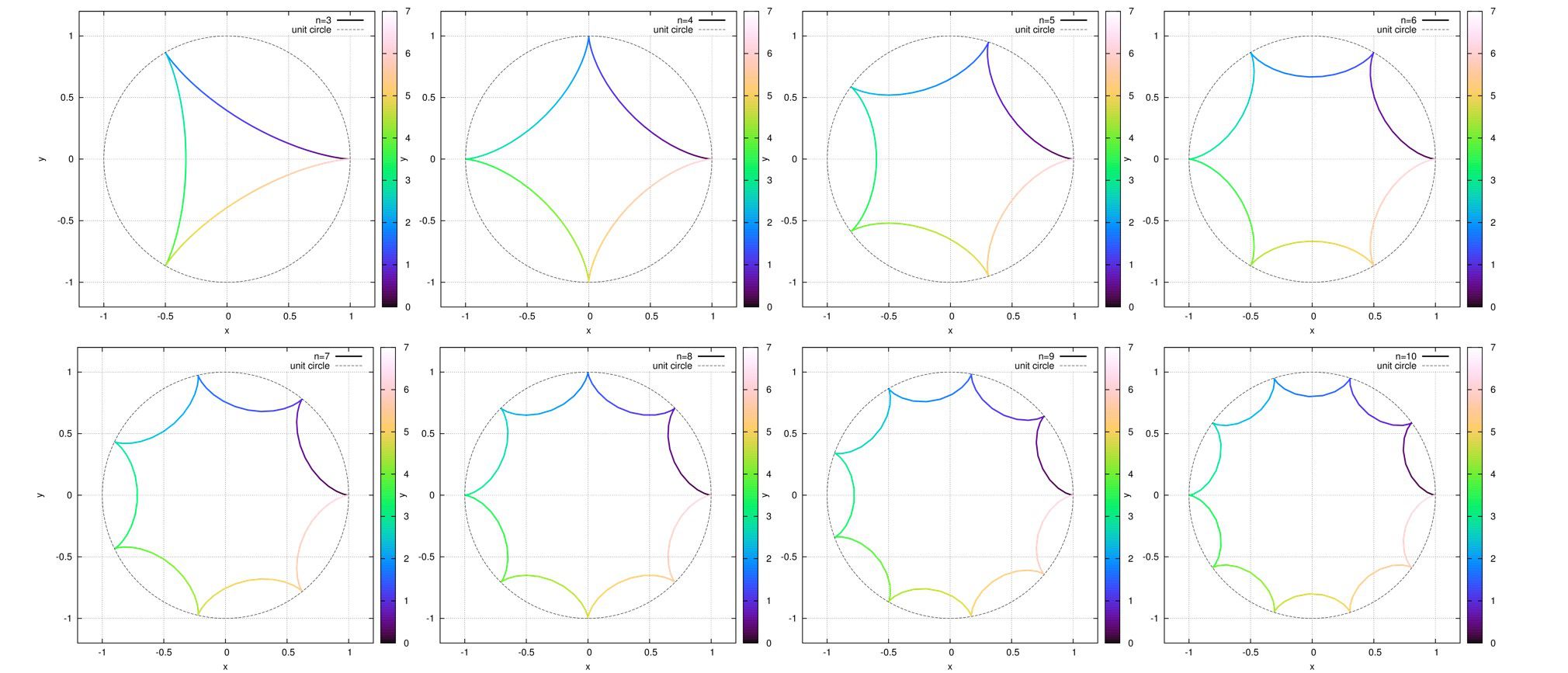
自由度hを少し変えてみましょう。
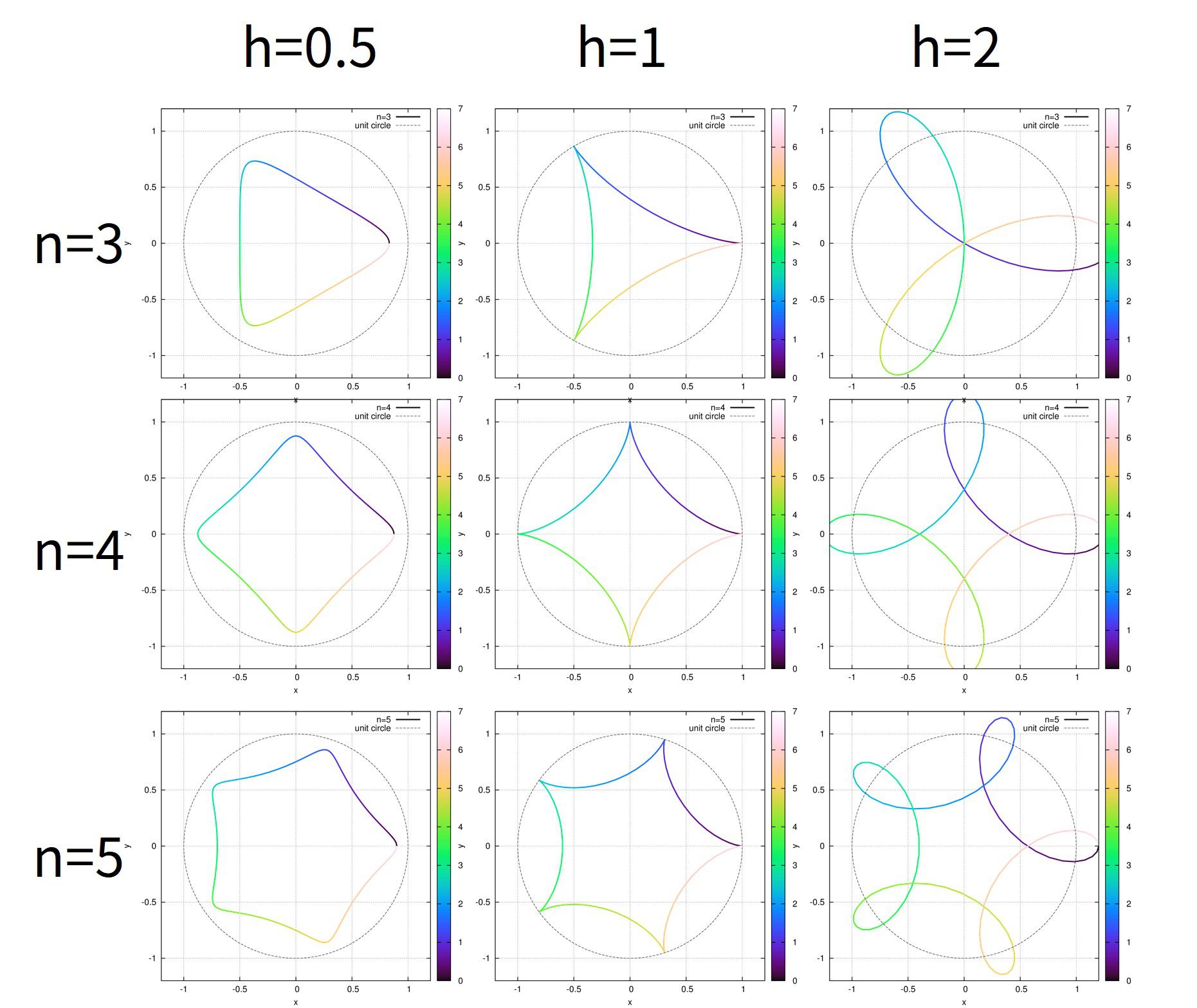
set param
set hidden3d
set size squ
set xr[-1.2:1.2]
set yr[-1.2:1.2]
set tr[0:2*pi]
set ticslevel 0
set grid
set xl "x"
set yl "y"
# +--- hypotrochoid ----+
# if h=1 --> hypocycloid
hcyc(n,h,t)=(real(n-1)*cos(t)+h*cos(t*real(n-1)))/real(n)
hcys(n,h,t)=(real(n-1)*sin(t)-h*sin(t*real(n-1)))/real(n)
h=1e0
plot hcyc(n,h,t),hcys(n,h,t)
# set table "d1.d"
# plot t,t*real(n-1)
# unset table
#
# set table "d2.d"
# splot "d1.d" u ((real(n-1)*cos($1)+h*cos($2))/real(n)):((real(n-1)*sin($1)-h*sin($2))/real(n)):($1)
# unset table
#
# plot "d2.d" u 1:2:3 w l lw 4 lc palette ti sprintf("n=%d",n), cos(t),sin(t) lc 8 ti "unit circle"
最後のコメントアウトを外すと、線の色を媒介変数に応じた色付けにできます。
トロコイド(3次元)
3次元の場合は多面体の時と同じように、平面のx,yの媒介変数によるトロコイドの関数をそれぞれhcyc(t),hcys(t)と置くと、
\(
\begin{equation}
\left\{
\begin{aligned}
x& = {\rm hcys}(u)\cdot {\rm hcyc}(v) \\
y& = {\rm hcys}(u)\cdot {\rm hcys}(v) \\
z& = {\rm hcyc}(u)
\end{aligned}
\right.
\end{equation}
\)
と書けます。
媒介変数\(u,v\)の範囲は(\(0\le u \lt \pi, \;\; 0\le v \lt 2\pi\))です。
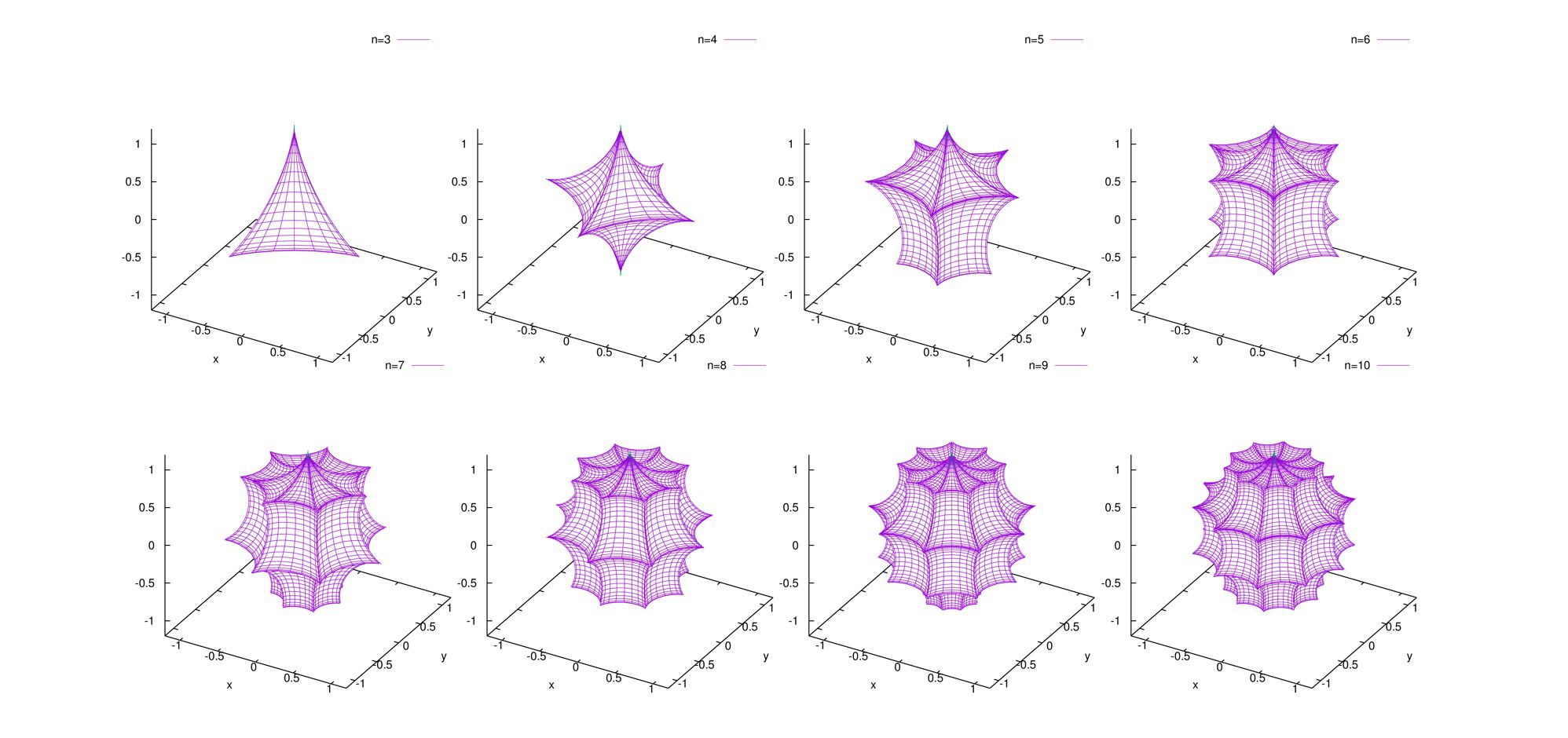
n=3,4,5,6
n=7,8,9,10の順です。
gnuplotスクリプトはこちら
set param
set hidden3d
set size squ
set xr[-1.2:1.2]
set yr[-1.2:1.2]
set zr[-1.2:1.2]
set tr[0:2*pi]
set ur[0:pi]
set vr[0:2*pi]
set ticslevel 0
set view equal xyz
set key
set xl "x"
set yl "y"
# +--- hypotrochoid ----+
# if h=1 --> hypocycloid
hcyc(n,h,t)=(real(n-1)*cos(t)+h*cos(t*real(n-1)))/real(n)
hcys(n,h,t)=(real(n-1)*sin(t)-h*sin(t*real(n-1)))/real(n)
hc3x(n,h,u,v)=hcys(n,h,u)*hcyc(n,h,v)
hc3y(n,h,u,v)=hcys(n,h,u)*hcys(n,h,v)
hc3z(n,h,u)=hcyc(n,h,u)
h=1e0
do for[n=3:10]{
set isosamples n*10+1
splot hc3x(n,h,u,v),hc3y(n,h,u,v),hc3z(n,h,u) ti sprintf("n=%d",n)
fn=sprintf("trocoid3d_n%dh%f",n,h)
print fn
# output file
set terminal postscript eps dashed enhanced color
set output fn.".eps"
replot
set out
set terminal wxt enhanced
#cv=sprintf("convert -density 400x400 -background white -flatten -alpha off %s.eps %s.png",fn,fn)
cv=sprintf("convert -density 400x400 %s.eps %s.png",fn,fn)
system cv
}
[adsense2]
スピログラフ(2次元)
スピログラフは遊んだ方も多いと思います。これです。

©Alexei Kouprianov/2007/CC-BY 2.5
スピログラフはトロコイドの特別な時です。スピログラフをもっと一般化したのがトロコイドです[2]。
図示すれば、スピログラフと言うのは
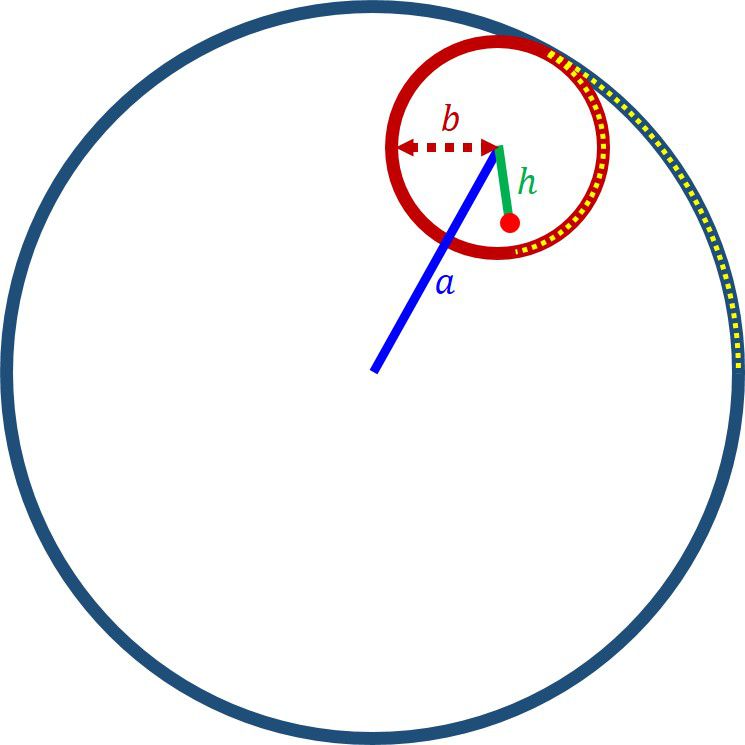
という二つの円からなる軌道です。黄色の点線の長さが等しい、という束縛条件が課せられます。
数式は上のトロコイドと同じで
\(
\begin{equation}
\left\{
\begin{aligned}
x& = \left[(n-1)\cos t +h\cos((n-1)t)\right]/n \\
y& = \left[(n-1)\sin t +h\sin((n-1)t)\right]/n
\end{aligned}
\right.
\end{equation}
\)
と書けます。
もう少し考えを一般化して、周りを取り囲んでいる形状が円ではない時を考えましょう。その時の数式を考えます。
考え方はトロコイドと一緒ですが、もう少し拡張しましょう。
今、2つの媒介変数による軌道を持っていたとします。1つの媒介変数の軌道上を動かせばスピログラフの考えと同じになります。図で示すと以下のようになります。
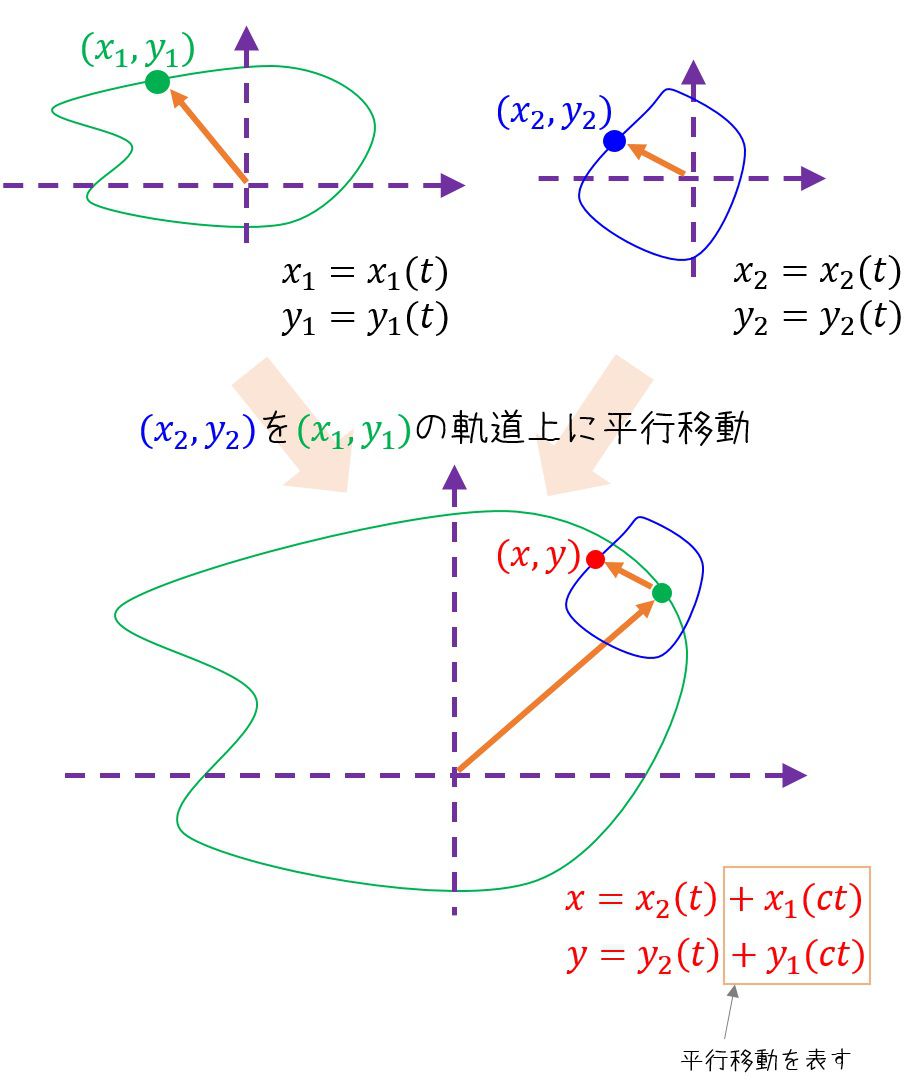
スピログラフは両方円であり、滑りが無い(cを決定する条件)場合に対応するわけです。ただ、円である必要性はないので、多角形であろうが、何だろうが数式上では書けるわけです。
興味深い事に、大きな軌道に沿って小さな軌道を動かした、と見ようが小さな軌道に沿って大きな軌道を動かしたとみても数式上では一緒なのです。面白いですね。
いくつか例を挙げます。
五角形上を動かす場合はこうです。
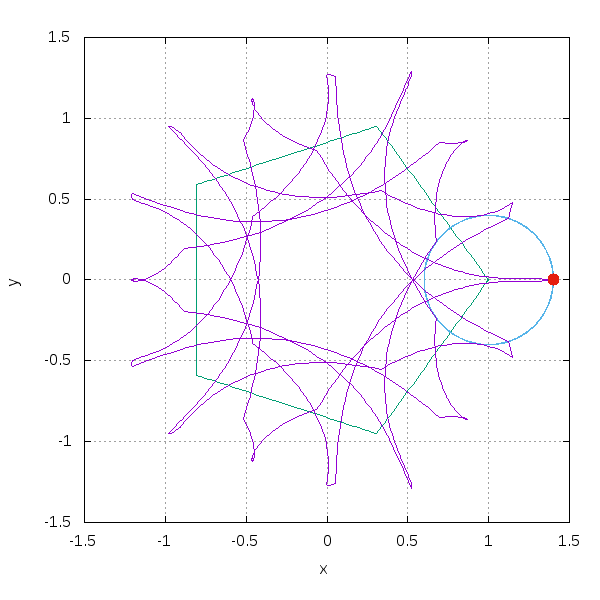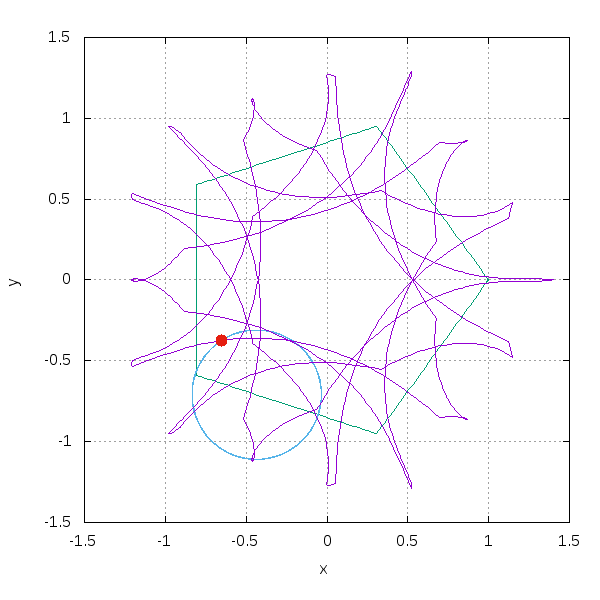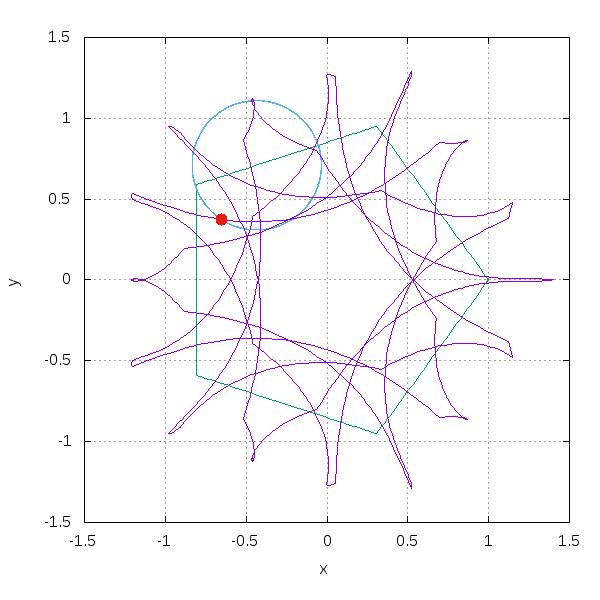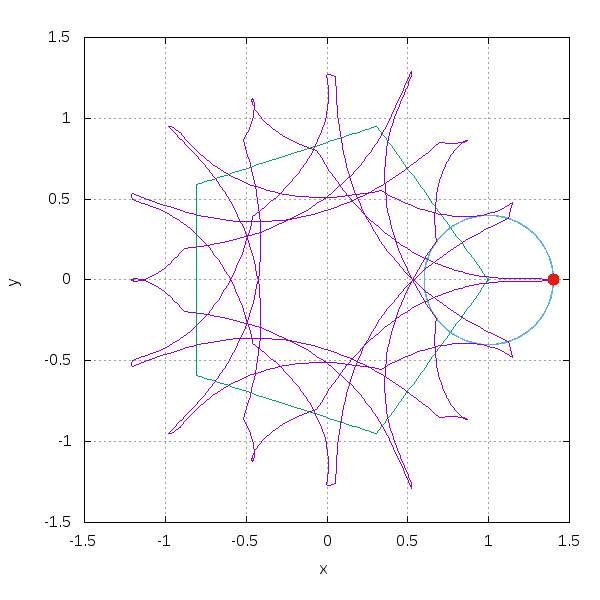
数式として,
\(
\begin{equation}
\left\{
\begin{aligned}
x& = f_{1x}(t)+r\cdot f_{2x}(s\cdot t) \\
y& = f_{1y}(t)+r\cdot f_{2y}(s\cdot t)
\end{aligned}
\right.
\end{equation}
\)
と書き表すことにします。これを元にgnuplotのスクリプトを書けば以下のようになります。
set param
set size ratio -1
set xl "x"
set yl "y"
set xr[-2:2]
set yr[-2:2]
unset key
# +---polygon---+
s1(x)=x-floor(x)
a(n)=2e0*pi/real(n)
cnp(n,t)=cos(a(n)*s1(t/a(n))-0.5e0*a(n))
pc(n,t)=cos(t)*cos(0.5e0*a(n))/cnp(n,t)
ps(n,t)=sin(t)*cos(0.5e0*a(n))/cnp(n,t)
p3x(n,u,v)=ps(n,u)*pc(n,v)
p3y(n,u,v)=ps(n,u)*ps(n,v)
p3z(n,u)=pc(n,u)
# ================
t1x(n,t)=pc(n,-t) # parametric function for polygon
t1y(n,t)=ps(n,-t) # parametric function for polygon
t2x(t)=cos(-r*t) # parametric function for circle
t2y(t)=sin(-r*t) # parametric function for circle
n=5 # shape of polygon
tm=5 # range of t
fs=50 # fineness about parameter
imax=300 # fineness about time
dt=tm*2e0*pi/real(imax)
set tr[0:tm*2*pi]
set samples (n*fs)*tm+1
np=2 # number of parametric functions
tx(i,t)=\
i == 1 ? pc(n,t) : ( \
i == 2 ? cos(t) : ( \
0 ))
ty(i,t)=\
i == 1 ? ps(n,t) : ( \
i == 2 ? -sin(t) : ( \
0 ))
stx(i,t)=word(ri,i)*tx(i,word(rt,i)*t)
sty(i,t)=word(ri,i)*ty(i,word(rt,i)*t)
#set term gif animate optimize delay 8 size 600,600
#set output 'parameter1.gif'
r=0.45e0
s=1.40e0
ri = ''
rt = ''
ri = ri . sprintf('%f %f', 1e0, r) # size of each parametric
rt = rt . sprintf('%f %f', 1e0, s) # rate of speed of t
do for [j=0:imax]{
tp=j*dt
plot sum[i=1:np] stx(i,t), \
sum[i=1:np] sty(i,t) lc 1, \
stx(1,t), \
sty(1,t) lc 2, \
stx(1,tp)+stx(2,t), \
sty(1,tp)+sty(2,t) lc 2, \
sprintf("< echo ''%f %f''", stx(1,tp)+stx(2,tp), sty(1,tp)+sty(2,tp)) ps 2 pt 7 lc 7
}
#set out
#set terminal wxt enhanced
色々に変化させた時の色々なときのグラフです。
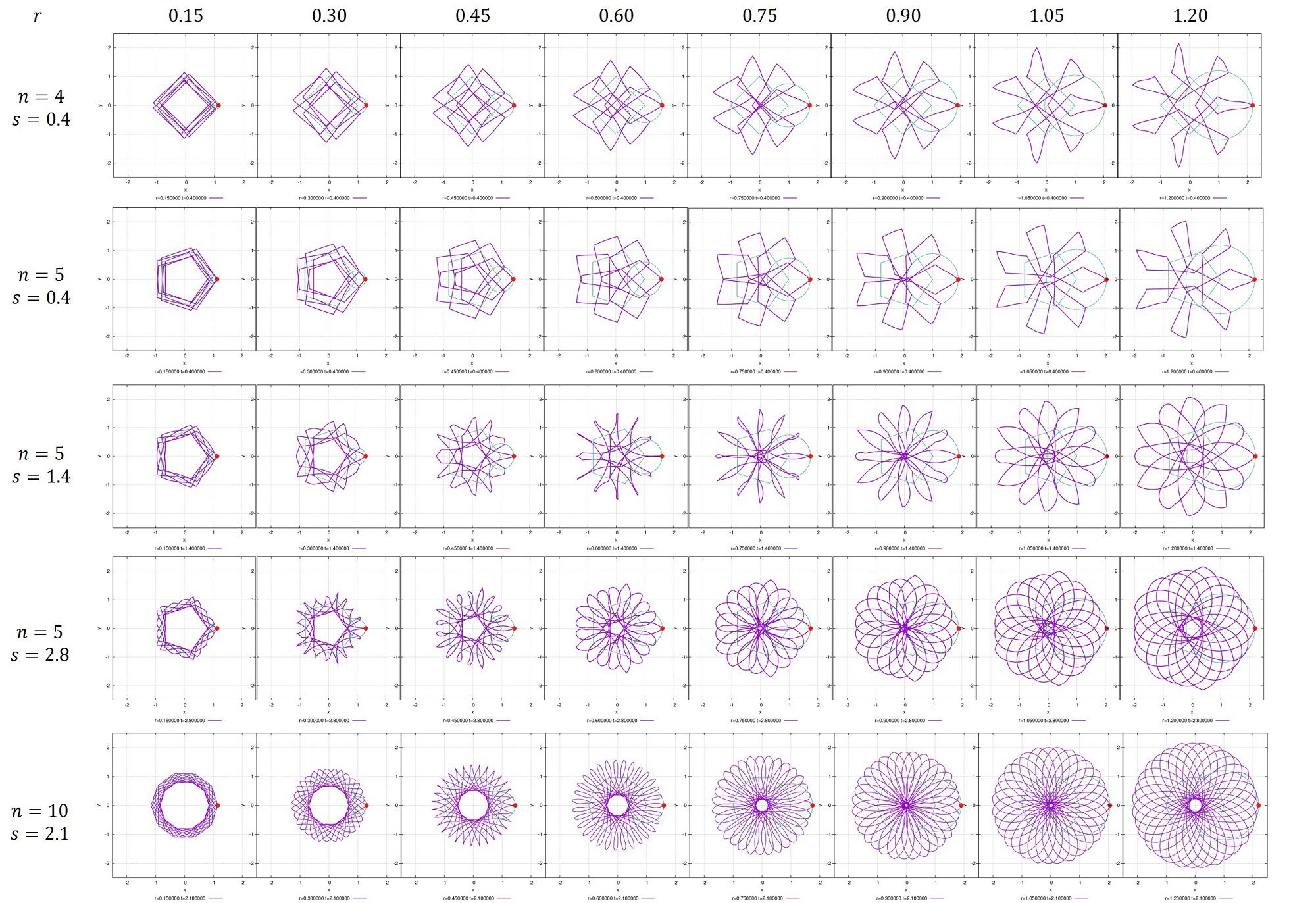
rを綺麗な数字にしなければもっと複雑な図が得られます。
また、この考え方は3つの媒介変数の軌道、4つの媒介変数の軌道…として容易に拡張できます。
もっと複雑な模様が欲しければ、もう少し増やしてみましょう。
例えば3つの場合はこうなります。
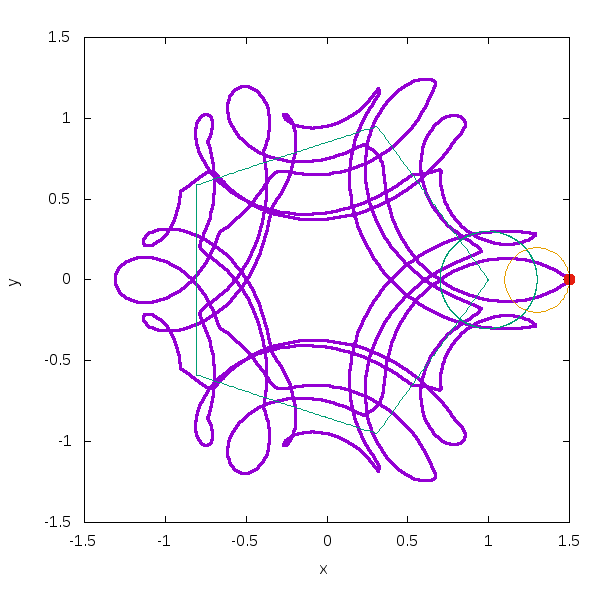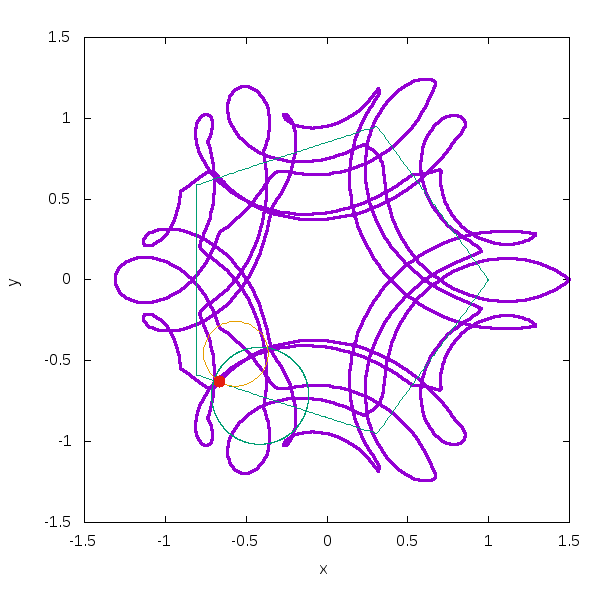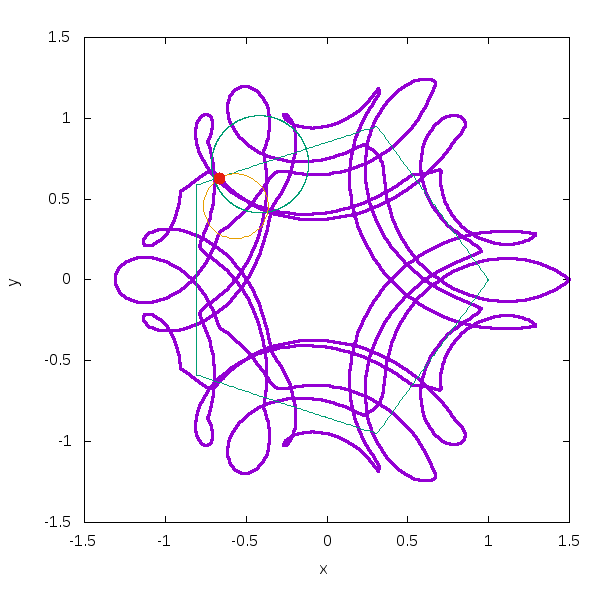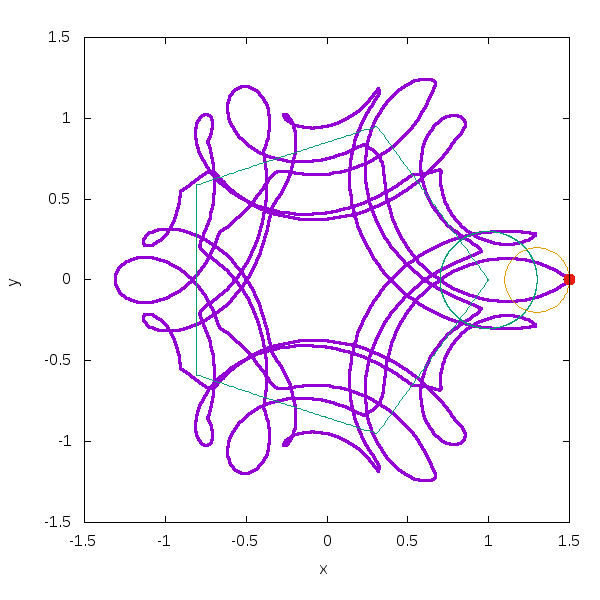
このスクリプトを置いておきます。
set param
set size ratio -1
set xl "x"
set yl "y"
set xr[-1.5:1.5]
set yr[-1.5:1.5]
unset key
# +---polygon---+
s1(x)=x-floor(x)
a(n)=2e0*pi/real(n)
cnp(n,t)=cos(a(n)*s1(t/a(n))-0.5e0*a(n))
pc(n,t)=cos(t)*cos(0.5e0*a(n))/cnp(n,t)
ps(n,t)=sin(t)*cos(0.5e0*a(n))/cnp(n,t)
p3x(n,u,v)=ps(n,u)*pc(n,v)
p3y(n,u,v)=ps(n,u)*ps(n,v)
p3z(n,u)=pc(n,u)
# ================
t1x(n,t)=pc(n,-t) # parametric function for polygon
t1y(n,t)=ps(n,-t) # parametric function for polygon
t2x(t)=cos(-r*t) # parametric function for circle
t2y(t)=sin(-r*t) # parametric function for circle
n=5 # shape of polygon
tm=5 # range of t
fs=50 # fineness about parameter
imax=300 # fineness about time
dt=tm*2e0*pi/real(imax)
set tr[0:tm*2*pi]
set samples (n*fs)*tm+1
np=3
ri='1e0 0.3e0 0.2e0' # size of each parametric
rt='1e0 2.2e0 5e0' # rate of speed of t
tx(i,t)=\
i == 1 ? pc(n,t) : ( \
i == 2 ? cos(t) : ( \
i == 3 ? cos(t) : ( \
0 )))
ty(i,t)=\
i == 1 ? ps(n,t) : ( \
i == 2 ? -sin(t) : ( \
i == 3 ? -sin(t) : ( \
0 )))
stx(i,t)=word(ri,i)*tx(i,word(rt,i)*t)
sty(i,t)=word(ri,i)*ty(i,word(rt,i)*t)
#set term gif animate optimize delay 8 size 600,600
#set output 'parameter1.gif'
do for [j=0:imax]{
tp=j*dt
plot sum[i=1:np] stx(i,t), \
sum[i=1:np] sty(i,t) lc 1, \
stx(1,t), \
sty(1,t) lc 2, \
stx(1,tp)+stx(2,t), \
sty(1,tp)+sty(2,t) lc 2, \
stx(1,tp)+stx(2,tp)+stx(3,t), \
sty(1,tp)+sty(2,tp)+sty(3,t) lc 4, \
sprintf("< echo ''%f %f''", stx(1,tp)+stx(2,tp)+stx(3,tp), sty(1,tp)+sty(2,tp)+sty(3,tp)) ps 2 pt 7 lc 7
}
#set out
#set terminal wxt enhanced
この考えを拡張していくと”フーリエ級数の図示化”と言うのができるわけです。
実際にやっている方がいるので紹介しておきますね。
参考文献
[1]Is there an equation to describe regular polygons? -MATHEMATICS
[2]Hypotrochoid -Wolfram Mathworld
[3]Is there an equation to describe regular polygons? -Mathematics
2021/11/29追記)滑らかに星と円を遷移する場合、このページが丁寧です。