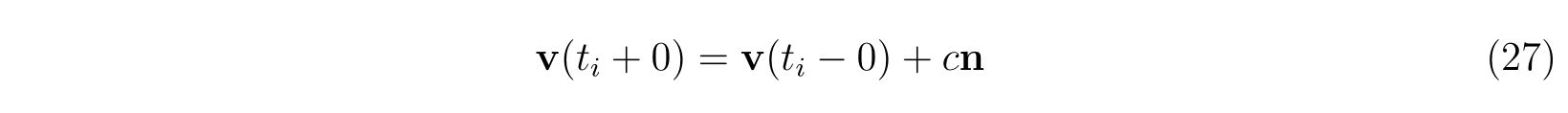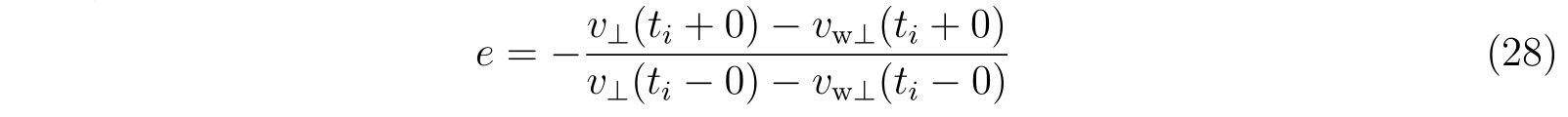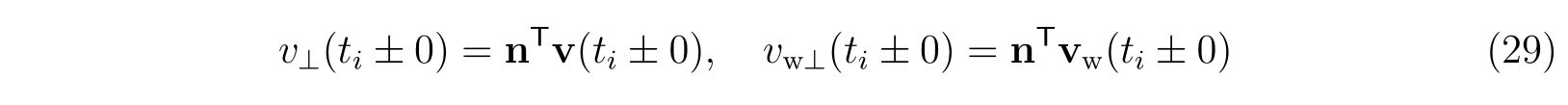program main
implicit none
integer::i,j,N,info,Nt
double precision::x,h,rktol,xbound,xstart
double precision::xa,xb,fwa,fwb
double precision,allocatable::y(:),ya(:),xarr(:)
double precision,external::fw
external::grk
double precision::pfx,pfy,pft,pfabs,nx,ny,els,cv
els=1d0
rktol=1d-8
N=4 ! Number of differential equations
allocate(y(1:N),ya(1:N))
xstart=0d0; xbound=20d0
y(1)=4d0 ! x (0)
y(2)=0d0 ! x'(0)
y(3)=4d0 ! y (0)
y(4)=5d0 ! y'(0)
Nt=201
allocate(xarr(1:Nt))
do j=1,Nt
xarr(j) = (j-1)*(xbound-xstart)/(Nt-1) + xstart
enddo
x = xarr(1)
xa = x
ya(1:N) = y(1:N)
fwa=fw(ya(1),ya(3),xa)
write(11,'(6e25.10e3)')xarr(1),y(1),y(2)&
,y(3),y(4),0.5d0*(y(2)**2+y(4)**2)+9.8*y(3)
i=1
do j=2,Nt
h=1d-6
info=0
xbound=xarr(j)
do while(info.le.0)
call drkf45(grk,x,h,N,y,xbound,info,rktol)
xb = x
fwb = fw(y(1),y(3),x)
if(i.ge.2.and.fwa*fwb.le.0d0)then
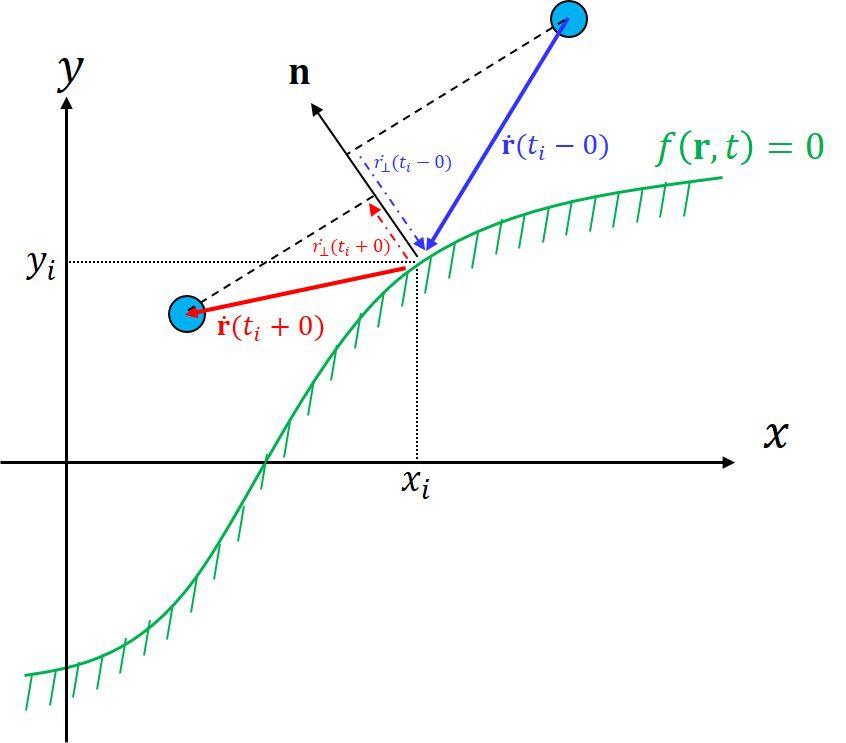
! Time when the mass point reflected by the wall
x = xa; y(1:N) = ya(1:N)
call ABstep(fw,N,grk,x,y,fwa,xb,fwb,rktol)
i=0; h=1d-6
if(abs(xbound-x).gt.1d-14)info=0
! Change the velocity
call pfw(y(1),y(3),x,pfx,pfy,pft)
pfabs = sqrt(pfx**2+pfy**2)
nx = pfx/pfabs
ny = pfy/pfabs
cv = -(1d0+els)*(nx*y(2)+ny*y(4)+pft/pfabs)
y(2) = y(2) + cv*nx
y(4) = y(4) + cv*ny
endif
write(10,'(6e25.10e3)')x,y(1),y(2)&
,y(3),y(4),0.5d0*(y(2)**2+y(4)**2)+9.8*y(3)
xa = x
ya(1:N) = y(1:N)
fwa = fwb
i = i+1
enddo
write(11,'(6e25.10e3)')xarr(j),y(1),y(2)&
,y(3),y(4),0.5d0*(y(2)**2+y(4)**2) +9.8*y(3)
enddo
stop
end program main
subroutine grk(N,x,y,f)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,y(1:N)
double precision,intent(out)::f(1:N)
double precision::g
g=9.8d0
f(1)=y(2)
f(2)=0d0
f(3)=y(4)
f(4)=-g
return
end subroutine grk
module GBLwall
implicit none
double precision,parameter::k=1d0
double precision,parameter::w=1d0
double precision,parameter::lx=5d0
double precision,parameter::ly=3d0
double precision,parameter::tphi=0d0 !dacos(-1d0)/2d0
double precision,parameter::xphi=-dacos(-1d0)/2d0
end module GBLwall
function fw(x,y,t)
use GBLwall
implicit none
double precision,intent(in)::x,y,t
double precision::fw
! example 1)
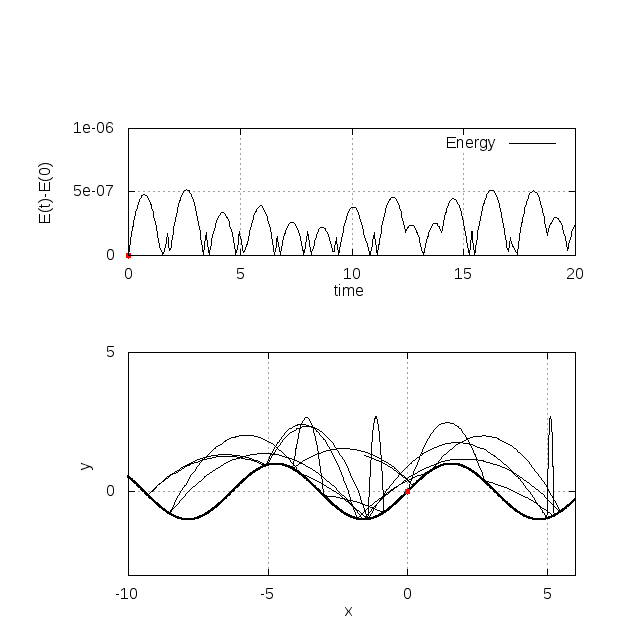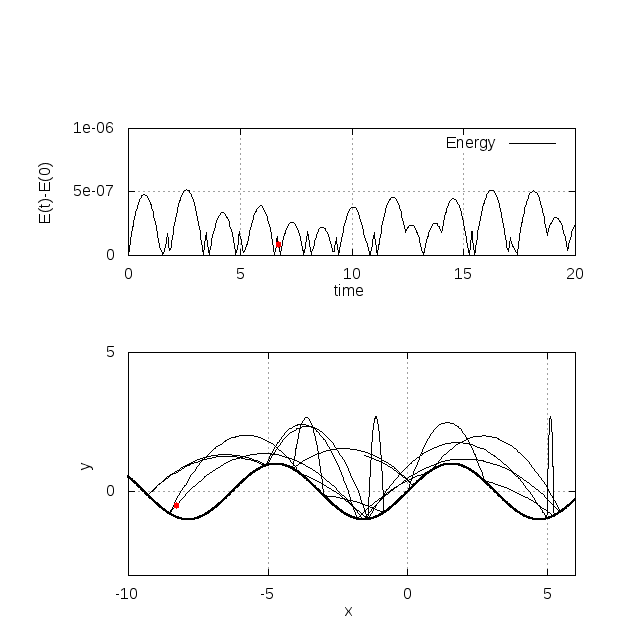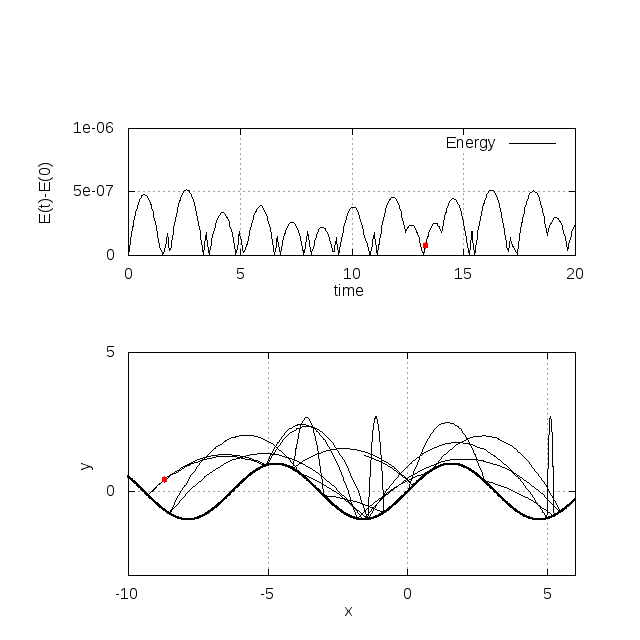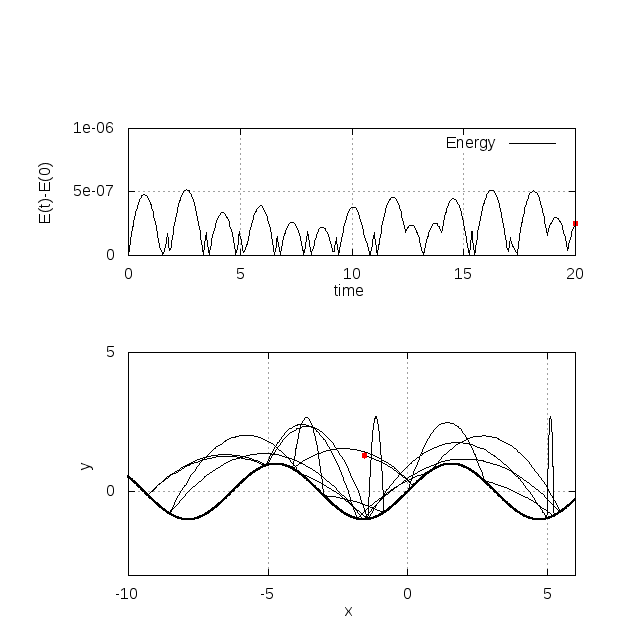
fw = y - sin(k*x+xphi)*sin(w*t+tphi)
! example 2)
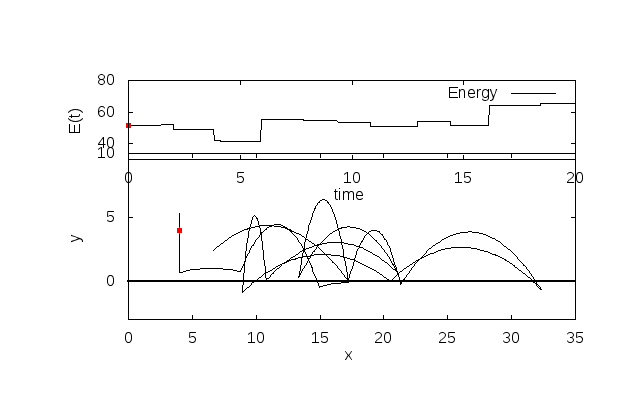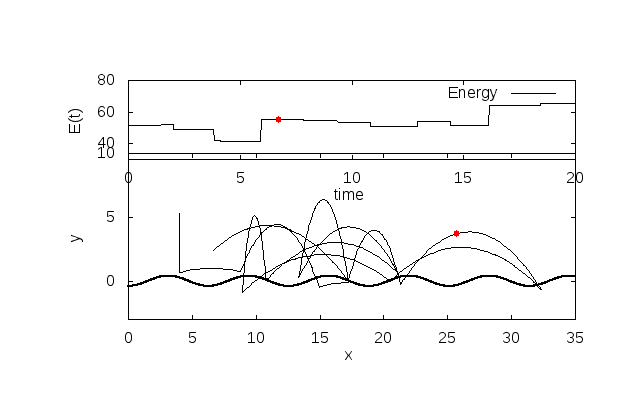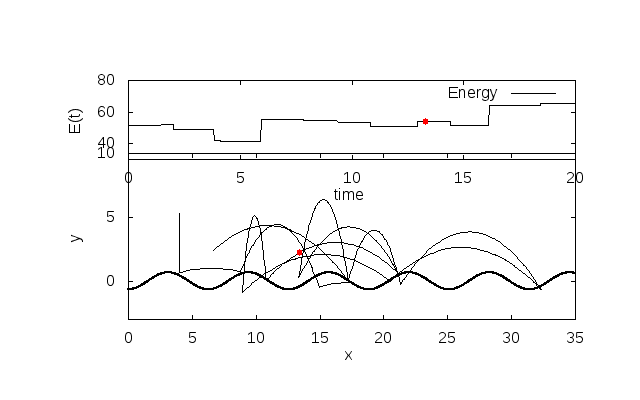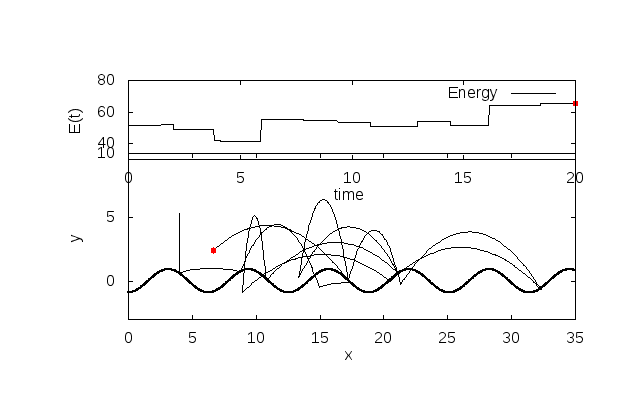
!fw = y - 2d0*t
! example 3)
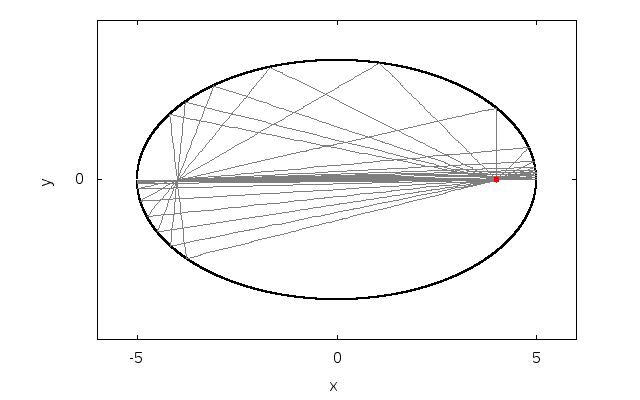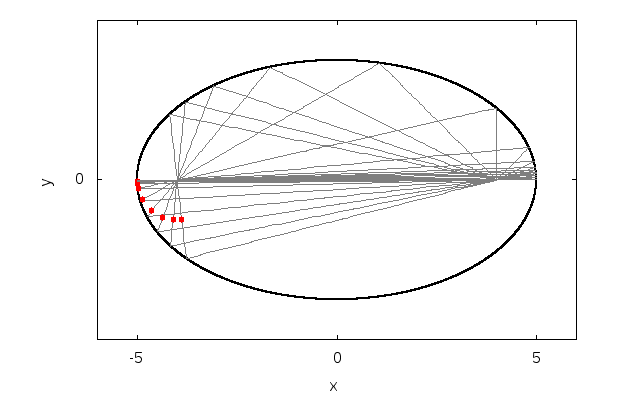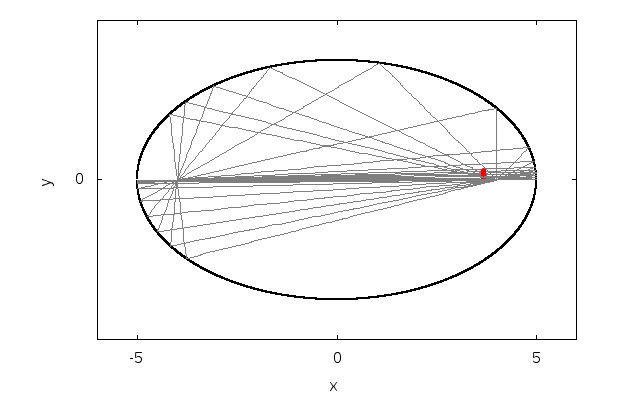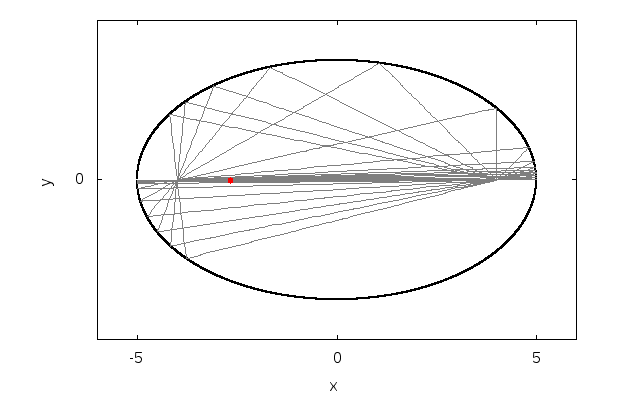
!fw = (x/lx)**2 + (y/ly)**2 - 1d0
! example 4)
!fw = (y-x)**2-1d0
return
end function fw
subroutine pfw(x,y,t,pfx,pfy,pft)
use GBLwall
implicit none
double precision,intent(in)::x,y,t
double precision,intent(out)::pfx,pfy,pft
! example 1)
pfx = -k*cos(k*x+xphi)*sin(w*t+tphi)
pfy = 1d0
pft = -w*sin(k*x+xphi)*cos(w*t+tphi)
! example 2)
!pfx=0d0
!pfy=1d0
!pft=-2d0
! example 3)
!pfx=2d0*x/(lx**2)
!pfy=2d0*y/(ly**2)
!pft=0d0
! example 4)
!pfx=-2*(y-x)
!pfy= 2*(y-x)
!pft=0d0
return
end subroutine pfw
!===============================
subroutine drkf45(grk,x,h,N,y,xbound,info,tol)
! if h < hmin, propagate forcibly with warning.
!
!-----------------
!info = -9 (maybe path the discontinue points)
! = 0 (Running now)
! = 1 (x reach xbound)
!-----------------
!
implicit none
integer,intent(in)::N
double precision,intent(in)::xbound,tol
double precision,intent(inout)::x,h,y(1:N)
integer,intent(inout)::info
integer::i,j,FLAG,key
double precision::R,delta,tx,Sy,err
double precision,allocatable::ty(:),K(:,:),tf(:)
double precision,parameter::hmin=1d-14,hmax=0.2d0
integer,parameter::s=6
double precision::a(1:s,1:s),b1(1:s),b2(1:s),c(1:s),Rc(1:s)
external::grk
c(1:6)=(/0d0, 0.25d0, 0.375d0,&
0.9230769230769230769230769230769230769231d0, 1d0, 0.5d0/)
a(1:6,1:6)=0d0
a(1,1:6)=(/0d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(2,1:6)=(/0.25d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(3,1:6)=(/0.09375d0, 0.28125d0, 0d0, 0d0, 0d0, 0d0/)
a(4,1:6)=(/0.8793809740555302685480200273099681383705d0, &
-3.277196176604460628129267182521620391443d0, &
3.320892125625853436504324078288575329995d0, 0d0, 0d0, 0d0/)
a(5,1:6)=(/2.032407407407407407407407407407407407407d0,-8d0, &
7.173489278752436647173489278752436647173d0, &
-0.2058966861598440545808966861598440545809d0, 0d0, 0d0/)
a(6,1:6)=(/-0.2962962962962962962962962962962962962963d0,2d0, &
-1.381676413255360623781676413255360623782d0, &
0.4529727095516569200779727095516569200780d0,-0.275d0,0d0/)
b2(1:6)=(/0.1185185185185185185185185185185185185185d0, 0.d0,&
0.5189863547758284600389863547758284600390d0, &
0.5061314903420166578061314903420166578061d0, &
-0.18d0, 0.03636363636363636363636363636363636363636d0/)
b1(1:6)=(/0.1157407407407407407407407407407407407407d0, 0d0,&
0.5489278752436647173489278752436647173489d0, &
0.5353313840155945419103313840155945419103d0, -0.2d0, 0d0/)
Rc(1:6)=(/0.002777777777777777777777777777777777777778d0,0d0, &
-0.02994152046783625730994152046783625730994d0, &
-0.02919989367357788410419989367357788410420d0, 0.02d0, &
0.03636363636363636363636363636363636363636d0/)
key=0
allocate(ty(1:N),tf(1:N),K(1:s,1:N))
ty=0d0; tf=0d0; K=0d0
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
endif
if(h.ge.abs(xbound-x))h=xbound-x
FLAG=1
if(abs(x-xbound).le.hmin)then
info=1
FLAG=0
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
ty(1:N)=y(1:N)
do i=1,j-1
ty(1:N)=ty(1:N)+K(i,1:N)*a(j,i)
enddo
call grk(N,tx,ty,tf)
K(j,1:N)=h*tf(1:N)
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i) &
+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R/dble(N))/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err.or.key.eq.1)then
x=x+h
y(1:N)=y(1:N)+b1(1)*K(1,1:N)+b1(3)*K(3,1:N) &
+b1(4)*K(4,1:N)+b1(5)*K(5,1:N)
FLAG=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
if(h.le.0d0.and.xbound-x.ge.0d0)then
info=1
FLAG=0
elseif(h.ge.0d0.and.xbound-x.le.0d0)then
info=1
FLAG=0
endif
enddo
deallocate(ty,tf,K)
return
end subroutine drkf45
subroutine ABstep(fw,N,grk,x,y,fwa,xb,fwb,rktol)
implicit none
integer,intent(in)::N
double precision,intent(inout)::x,y(1:N)
double precision,intent(inout)::fwa,xb,fwb
double precision,intent(in)::rktol
double precision,external::fw
external::grk
integer::k,info
integer,parameter::ktmax=50
double precision::xa,fwc,m,xc,h,tol1,xm
double precision,allocatable::ya(:)
double precision,parameter::eps=epsilon(1d0)
double precision,parameter::tol=1d-6
! Must satisfy fwa*fwb < 0
allocate(ya(1:N))
ya(1:N) = y(1:N)
xa = x
! Rootfind by (Anderson & Bj"ork's method)
do k=1,ktmax
x = xa
y(1:N) = ya(1:N)
xc = xa-fwa*(xa-xb)/(fwa-fwb)
h = xc-x
info = 0
do while(info.le.0)
call drkf45(grk,x,h,N,y,xc,info,rktol)
enddo
fwc = fw(y(1),y(3),xc)
if(fwa*fwc.gt.0d0)then
! Substitute a by c
if(fwc/fwa.lt.1d0)then
m=1d0-fwc/fwa
else
m=0.5d0
endif
fwb=m*fwb
xa = xc
ya(1:N) = y(1:N)
fwa = fwc
else
! Substitute b by c
if(fwc/fwb.lt.1d0)then
m=1d0-fwc/fwb
else
m=0.5d0
endif
fwa=m*fwa
xb = xc
fwb = fwc
endif
tol1 = 2.0d0*eps*dabs(xc)+0.5d0*tol
xm = 0.5d0*(xa-xb)
if ((dabs(xm).le.tol1).or.(fwc.eq.0d0))exit
enddo
return
end subroutine ABstep