\begin{align}
\int_{-\infty}^{\infty} \theta(x)e^{-ikx}dx
=\lim_{\varepsilon\to +0}\frac{1}{i}\frac{1}{k- i\varepsilon}
=\frac{1}{i}\frac{1}{k- i0}
\end{align}
を導出します。
ここでは、アーベル総和の考えを用いません。使うのはフーリエ変換のユニタリー性です。
※いろいろ数学的に自信が持てない点があります。これは僕が納得した解釈であるので、完全に正しい導出方法ではないかもしれません。
また、ここではフーリエ変換を
\(
\begin{align}
& g(k)=\int_{-\infty}^{\infty}f(x)e^{-ikx} dx \\
& f(x)=\int_{-\infty}^{\infty}g(k)e^{ikx} \frac{dk}{2\pi}
\end{align}
\)
で定義しています。
その他フーリエ変換
ヘヴィサイド関数のフーリエ変換 ← 今ここ
1のフーリエ変換
\(x\)のフーリエ変換
\(1/x\)のフーリエ変換
\(1/(x^n)\)のフーリエ変換
ヘヴィサイド関数のフーリエ変換
ヘヴィサイド関数\(\theta(x)\)は
\(
\begin{eqnarray}
\theta(x) =
\left\{
\begin{aligned}
0~~~(x\gt 0)\\
1~~~(x\lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
と定義されます。この関数のフーリエ変換、すなわち積分
\(
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx
\)
を考えます。上の積分は\(x\lt 0\)ではヘヴィサイド関数はゼロなので、
\(
\begin{align}
\int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx=\int_{0}^{\infty}e^{-ikx}dx
\end{align}
\)
となります。後はこの積分が計算出来れば良いです。
\(k\ne0\)の場合
もしも\(k\ne 0\)であれば、この積分は計算可能です。
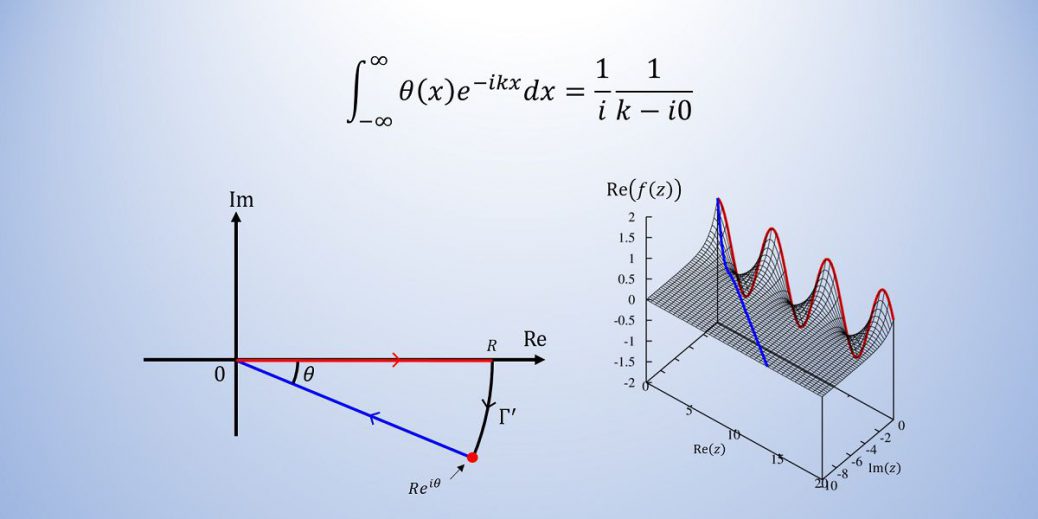
被積分関数を複素x平面に解析接続して、以下の図のような閉経路を考えます。
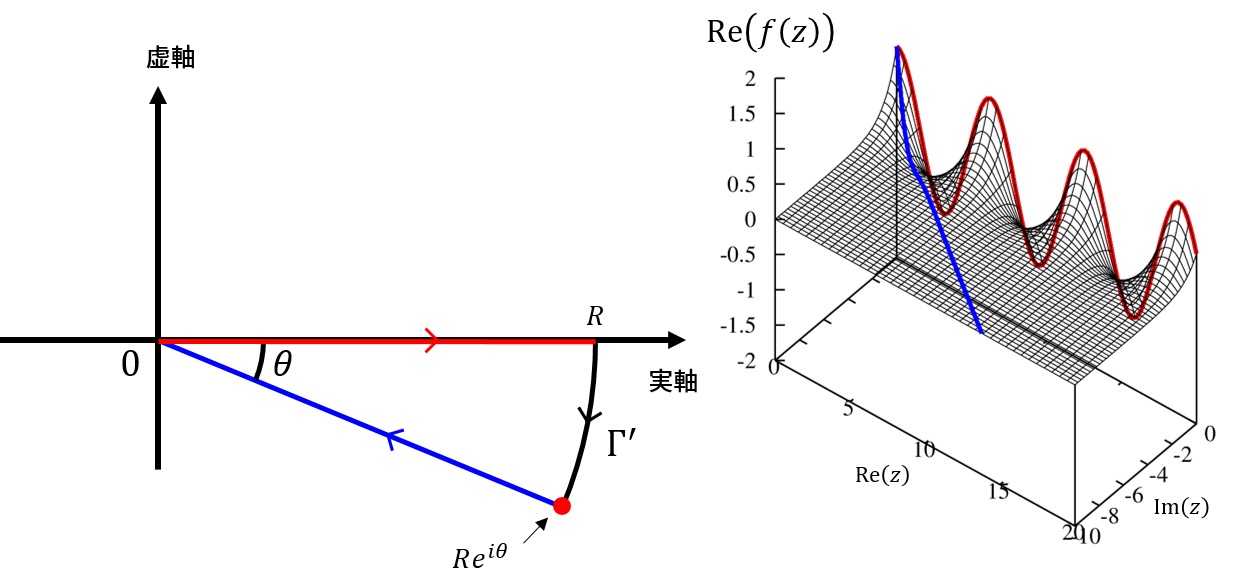
今、閉経路内に特異点は無いので、一周回った時の周回積分の値はゼロです。また、大きく外側を回る経路\(\Gamma’\)は、被積分関数が漸近で収束する領域なので、無限遠方での線積分の値はゼロです。このことから、
\(
\begin{align}
\oint f(x) dx &= \lim_{R\to\infty} \left[\int_0^R f(x)dx + \int_{\Gamma’}f(x)dx+\int_{R}^0 f(re^{i\theta})re^{i\theta}dr\right]\nonumber \\
0&= \lim_{R\to\infty}\left[ \int_0^R f(x)dx +\int_{R}^0 f(re^{i\theta})re^{i\theta}dr\right] \nonumber\\
\lim_{R\to\infty} \int_0^R f(x)dx &=\lim_{R\to\infty}\int_{0}^R f(re^{i\theta})re^{i\theta}dr \nonumber
\end{align}
\)
が成立します。
\(e^{-ikx}\)で\(k\ne 0\)の場合、
\(\pi \lt \theta\lt 0 (k\gt 0),~~0 \lt \theta\lt \pi (k\lt 0) \)では
\(
\begin{align}
\int_0^{\infty}e^{-ikx}dx &= \lim_{R\to\infty}\int_0^{R e^{i\theta}}e^{-ikz}dz \nonumber \\
&= \lim_{R\to\infty}\left[\frac{e^{-ikz}}{-ik}\right]^{R e^{i\theta}}_{0} \nonumber \\
&=\frac{1}{i}\frac{1}{k}
\end{align}
\)
となります。
しかし、\(k=0\)は漸近で収束しないので同様の方法で計算することができません。
\(k=0\)の場合
\(k=0\)で、被積分関数は無限大に発散します。
なぜなら、
\(
\begin{align}
\int_{0}^{\infty}e^{-i0x}dx= \int_{0}^{\infty}dx =\infty
\end{align}
\)
だからです。ここで問題なのは、無限大への発散の仕方です。
これが示すことは、フーリエ変換後の空間で\(k=0\)は特異点ということです。
以上から
\(
\begin{eqnarray}
\int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx =
\left\{
\begin{aligned}
\frac{1}{i}\frac{1}{k}~~~(k\ne 0)\\
\infty~~~(k= 0)
\end{aligned}
\right.
\end{eqnarray}
\)
というフーリエ変換結果を得ました。
特異点の周り方の指定
さて、前回の計算結果から、\(k=0\)に特異点がある事が分かりました。
この特異点の性質を知るために、逆フーリエ変換を考えます。
なぜなら、フーリエ変換はユニタリー変換であることを考えれば、フーリエ変換した関数を逆フーリエ変換した時には元に戻っていて欲しい、という条件が課されているからです。
そして、逆フーリエ変換時にはこれを避けて回らねばならりません。
特異点を回る方法として考えられるのは以下の3つです。
- 複素k平面上で特異点周りを上方向を回る
- 複素k平面上で特異点周りを下方向を回る
- 複素k平面上で特異点周りを上方向と下方向を回った結果の平均をとる
結果的に正しいのは下方向を回った時の2です。そしてこの特異点を回る方法をフーリエ変換後の結果に含めると、
\(
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \lim_{\varepsilon \to +0 }\frac{1}{i}\frac{1}{k-i\varepsilon}
\)
という結論を得ることが出来ます。
ここで、\(-i\varepsilon\)が意味するのは、複素k平面を積分する時には下方向を回りなさい、ということを数学的に表しています。
実際にそれぞれ計算して確かめてみましょう。
被積分関数が漸近で収束する領域は\(e^{ikx}\)なので
\(x\gt 0\)の時、複素k平面の上半面、
\(x\lt 0\)の時、複素k平面の下半面になります。
一位の特異点を閉経路内に含み、正の方向に回る場合、コーシーの積分定理より値は\(2\pi i\)です。
1. 複素k平面上で特異点周りを上方向を回る場合
フーリエ変換後の関数\(f(x)\)は
\(
\begin{eqnarray}
f(x)=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{-i}{k+i\varepsilon}e^{ikx}\frac{dk}{2\pi} =
\left\{
\begin{aligned}
1~~~(x\lt 0) \\
0~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
なので、これは元のヘヴィサイド関数ではないので特異点を回る方法として欲しいものではありません。
2. 複素k平面上で特異点周りを下方向を回る
フーリエ変換後の関数\(f(x)\)は
\(
\begin{eqnarray}
f(x)=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{-i}{k-i\varepsilon}e^{ikx}\frac{dk}{2\pi} =
\left\{
\begin{aligned}
0~~~(x\lt 0) \\
1~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
なので、これはフーリエ変換前のヘヴィサイド関数に一致します。よってこれが適切です。
3. 複素k平面上で特異点周りを上方向と下方向を回った結果の平均をとる
フーリエ変換後の関数\(f(x)\)は1. 2. の結果から、
\(
\begin{eqnarray}
f(x)=\left\{
\begin{aligned}
1/2~~~(x\lt 0) \\
1/2~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
なので、これは元のヘヴィサイド関数ではないので特異点を回る方法として欲しいものではありません。
以上から、複素k平面上の\(k=0\)にある特異点の回り方を指定して、ヘヴィサイド関数
\(
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \lim_{\varepsilon \to +0 }\frac{1}{i}\frac{1}{k-i\varepsilon}
\)
と導くことが出来ます。良く、\(\varepsilon\to 0\)の表記を省略して
\(
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \frac{1}{i}\frac{1}{k-i0}
\)
と記述されます。
演算子としての表現
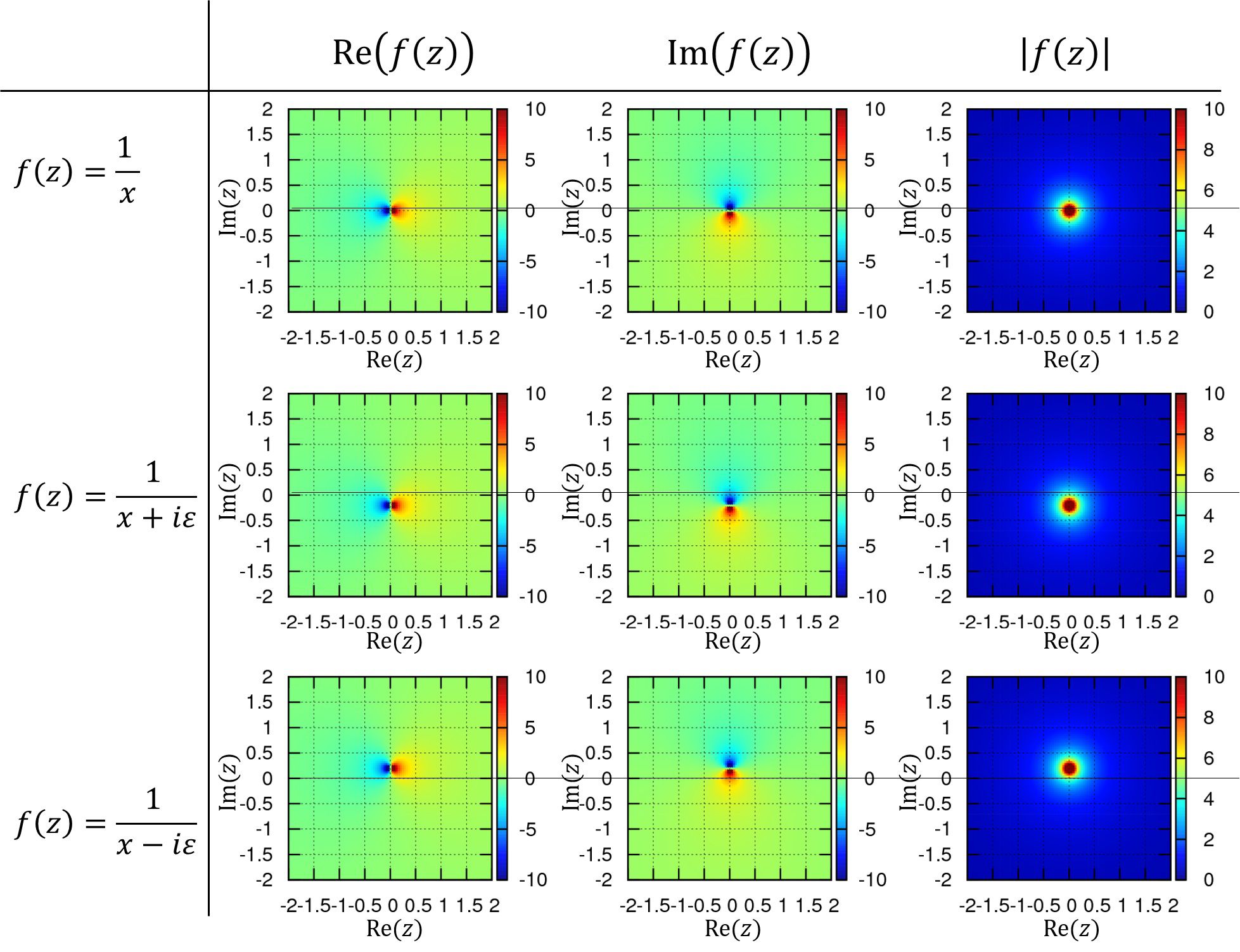
ヘヴィサイド関数のフーリエ変換後の結果
\(
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \frac{1}{i}\frac{1}{k-i0}
\)
の右辺に現れる特徴的な量
\(
\displaystyle \frac{1}{k-i0}
\)
を演算子として捉えた場合を考えます。この時、\(k\)を\(x\)に入れ替えて、ある関数\(f(x)\)に作用させると
\(
\begin{align}
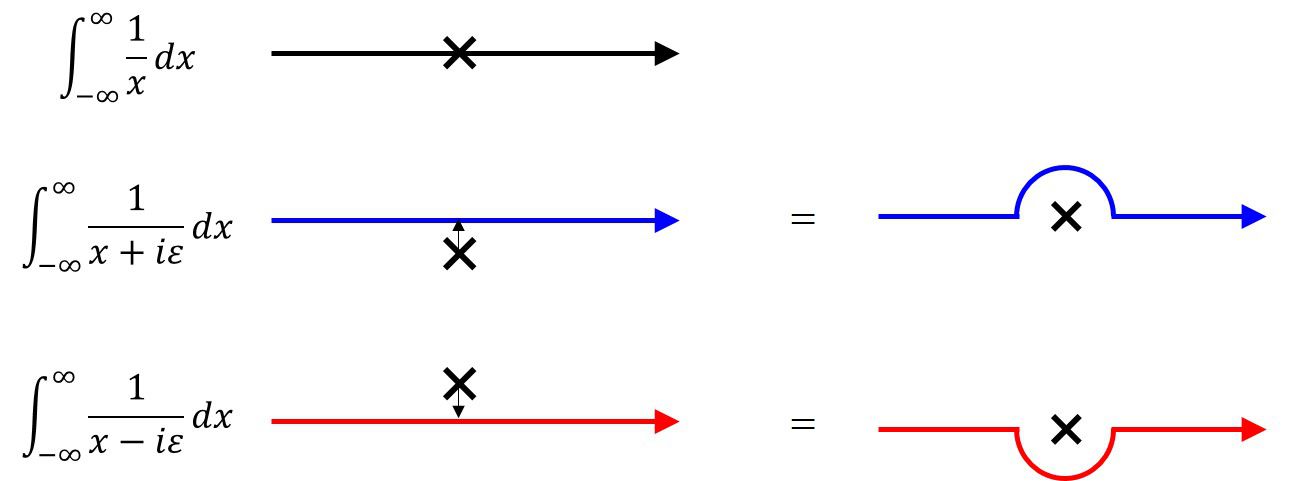
\int_{-\infty}^{\infty} \left(\frac{1}{x-i0}\right) f(x)dx&=
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{f(x)}{x-i\varepsilon} dx\nonumber \\
&=\lim_{R\to \infty}
\left[\int_{-R}^{-\varepsilon’} \frac{f(x)}{x} dx+\int_{\Gamma_-} \frac{f(x)}{x}dx+\int_{\varepsilon’}^{R} \frac{f(x)}{x}dx\right]
\end{align}
\)
となります。
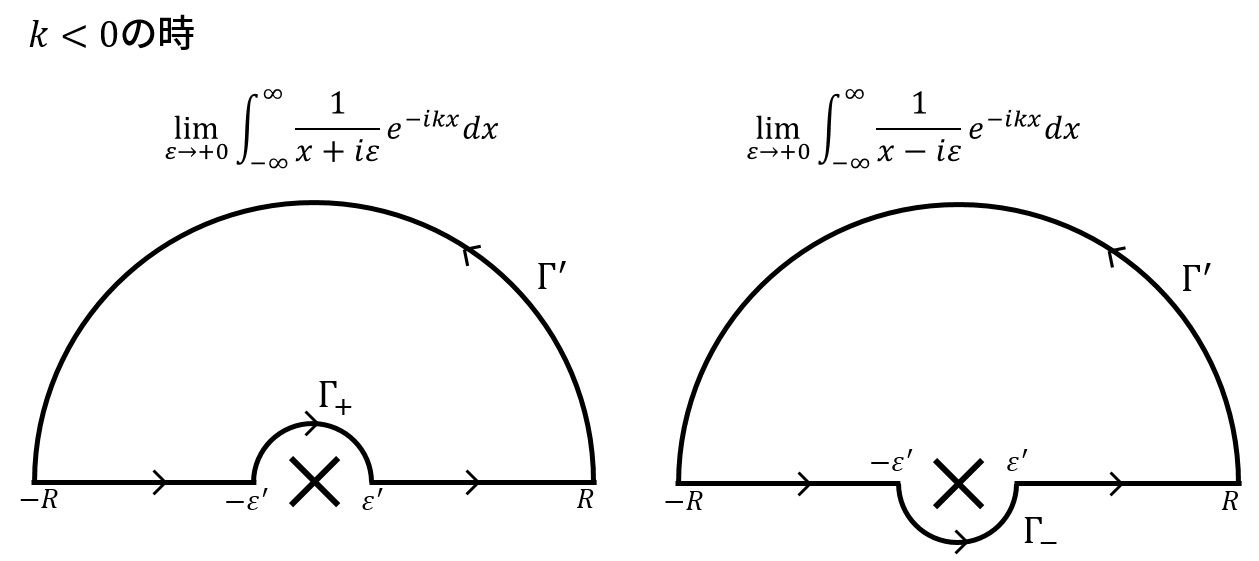
ここで、\(\Gamma_-\)は特異点を下に回る経路です。
注記しますが、コーシーの積分定理があるため、この段階で\(\varepsilon’\)をゼロに近づける必要は全くありません。
特に\(\lim_{\varepsilon’\to +0}\)を考えますと、コーシーの主値を用いて
\(
\begin{align}
&=\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x} dx +\pi i f(0)\nonumber \\
&=\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x} dx +\pi i \int_{-\infty}^{\infty}f(x)\delta(x)dx \nonumber \\
&=\int_{-\infty}^{\infty}\left(\mathcal{P} \frac{1}{x}+\pi i \delta(x)\right) f(x)dx \nonumber
\end{align}
\)
と書き表せます。以上から、右辺に現れる特徴的な量は
\(
\begin{align}
\frac{1}{x-i0}=\mathcal{P} \frac{1}{x}+\pi i \delta(x)
\end{align}
\)
と書き換えて解釈しても良い、となります。