set palette defined ( 0 '#000090',1 '#000fff',2 '#0090ff',3 '#0fffee',4 '#000000',5 '#ffee00',6 '#ff7000',7 '#ee0\
000',8 '#7f0000')
unset label
set xr[-1e5:1e5]
set yr[-1e5:1e5]
fname = sprintf("n%d_l%d_m%d",$0,$1,$2)
stats "dat/".fname.".d" u 1:3 name "hatom" nooutput
#set title sprintf("(%d,%d,%d)",$0,$1,$2)
set xl "x[a.u.]" offset 0,0.5
set yl "z[a.u.]" offset 0.2,0
rr=hatom_max_x
if(rr < 100e0){
rr=floor(hatom_max_x*0.1e0)*10e0
rr=rr+10e0
if(rr > hatom_max_x){rr=hatom_max_x}
}else{
rr=floor(hatom_max_x*0.01e0)*100e0
}
if(rr < 10e0){rr=10e0}
set xr[-rr:rr]
set yr[-rr:rr]
print hatom_max_y
t=hatom_max_y
count=1e0
while(t <= 1e0){
t=t*10
count=count*0.1e0
}
t=floor(t)+1e0
t=t*count
n=$0
l=$1
m=$2
if(n == 3){if(t > 0.05){
t=0.05
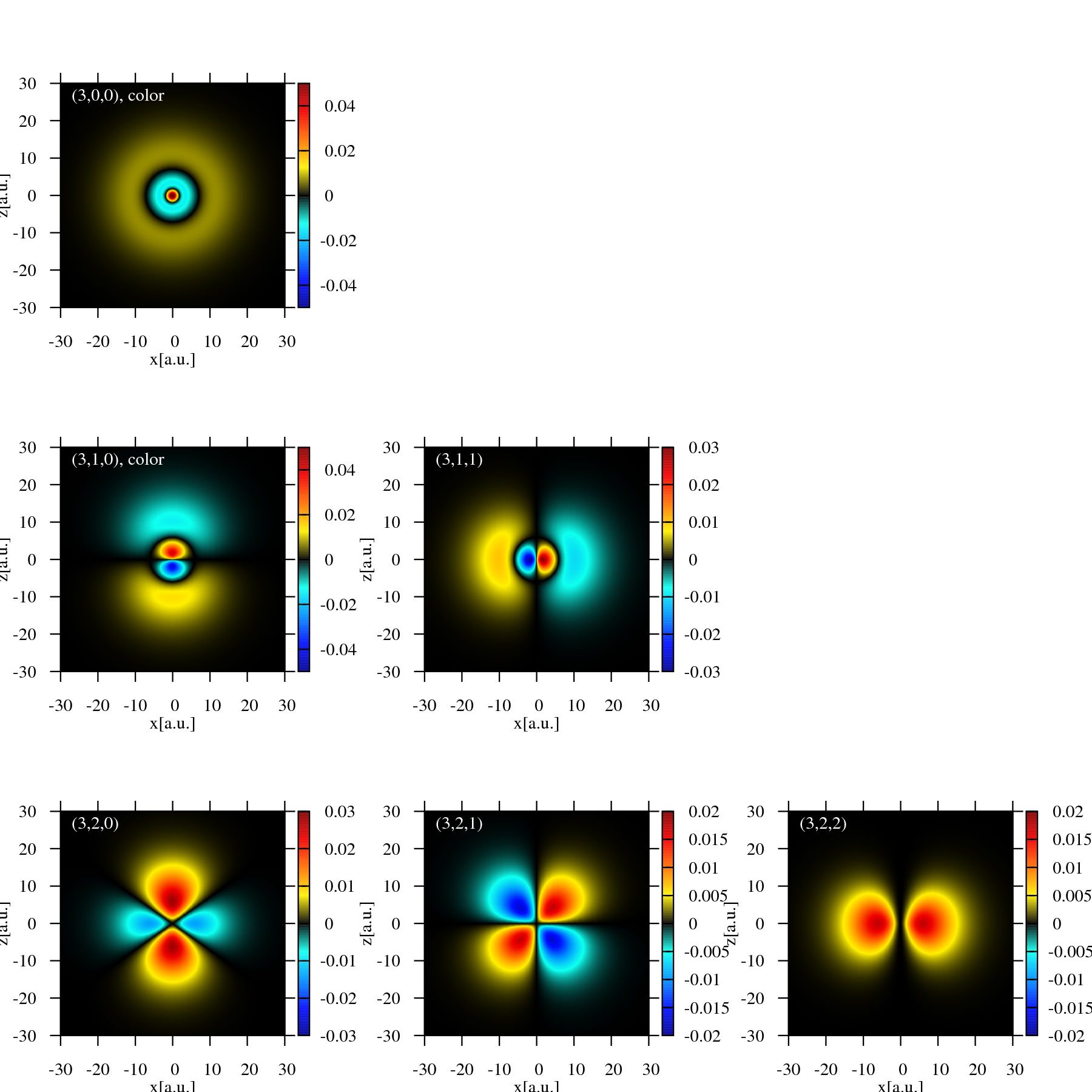
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 4){if(t > 0.02){
t=0.02
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 5){if(t > 0.01){
t=0.01
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 6){if(t > 0.008){
t=0.008
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 7){if(t > 0.006){
t=0.006
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 8){if(t > 0.005){
t=0.005
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 9){if(t > 0.003){
t=0.003
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 10){if(t > 0.002){
t=0.002
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 11){if(t > 0.002){
t=0.002
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 12){if(t > 0.002){
t=0.002
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 13){if(t > 0.001){
t=0.001
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 14){if(t > 0.001){
t=0.001
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 15){if(t > 0.001){
t=0.001
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 16){if(t > 0.0008){
t=0.0008
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 17){if(t > 0.0006){
t=0.0006
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 18){if(t > 0.0006){
t=0.0006
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 19){if(t > 0.0005){
t=0.0005
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
if(n == 20){if(t > 0.0004){
t=0.0004
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d), color",$0,$1,$2)
}else{
set label tc rgb "white" at graph 0.05,graph 0.95 front sprintf("(%d,%d,%d)",$0,$1,$2)
}}
set cbr[-t:t]
set tics out
set cbtics in
unset key
set size ratio -1
set pm3d map
splot sprintf("dat/n%d_l%d_m%d.d",$0,$1,$2) u 1:2:3
unset label