ここではゼータ関数を数値計算で得るためのアルゴリズムとfortran90によるプログラムを載せています。

目次

1. ゼータ関数の級数表示
2. プログラム(fortran90)
3. 計算データ
4. グラフ
5. 非自明、自明なゼロ点
6. ゼータ関数の導関数とプログラム

ゼータ関数の計算方法

ゼータ関数は通常
・\(\rm{Re}(s)\gt 1\)に対しては直接計算を行い、\(\rm{Re}(s)\le 1\)の領域に対しては相反公式
\(
\displaystyle \zeta(s)=2^{s}\pi^{s-1}\sin\left(\frac{\pi s}{2}\right)\Gamma(1-s)\zeta(1-s)
\)
を使って求める事が推奨されます。
ガンマ関数を使うことを避けたい場合、全複素平面(\(s\ne 1\))で有効なゼータ関数の表示
\(
\displaystyle
\zeta(s)=\frac{1}{1-2^{1-s}}
\sum_{n=0}^{\infty} \frac{1}{2^{n+1}}
\sum_{k=0}^{n} {n \choose k} \frac{(-1)^k}{(k+1)^s}
\)
を使うのが良いでしょう。

ゼータ関数の級数表示

ゼータ関数は
\(
\displaystyle
\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s} ,~~~(1\lt s)
\)
と定義されます。が、これはlogの収束であるため非常に収束が遅いです。
Euler-Knopp変換
\(\displaystyle
\sum_{n=0}^\infty a_n = \sum_{n=0}^{\infty} \frac{1}{(1+q)^{n+1}}
\sum_{j=0}^{n}{n \choose j} q^{n-j}a_j
\)
(q=1のときEuler変換)によって早く収束する級数に変換されます[4]。
より詳しい証明は[5]。

Riemann Zeta Function — from Wolfram MathWorld, Eq.(21)
によると、全領域(s=1以外)で収束するリーマンのゼータ関数の級数表示は、
\(
\displaystyle
\zeta(s)=\frac{1}{1-2^{1-s}}
\sum_{n=0}^{\infty} \frac{1}{2^{n+1}}
\sum_{k=0}^{n} {n \choose k} \frac{(-1)^k}{(k+1)^s}
\)
と書けます。もう一つ形式があるのですが、そちらは収束が遅そうな形式だったので用いていません。

数値計算的には2の乗数とかはあまり計算したくありません。そこで、漸化式を考えます。
\(
\begin{align}
\zeta(s) &=\sum_{n=0}^{\infty} b_n \\
b_n &= \sum_{k=0}^{n}a_k^n \\
a_k^n &= \frac{1}{1-2^{1-s}}\frac{1}{2^{n+1}}{n \choose k}\frac{(-1)^k}{(k+1)^s}
\end{align}
\)
と\(b_n, a_k^n\)を定義します。\(a_k^n\;\; (n\ge k)\)を計算するために漸化式を考えると

と導く事が出来ます。
計算手順としては、

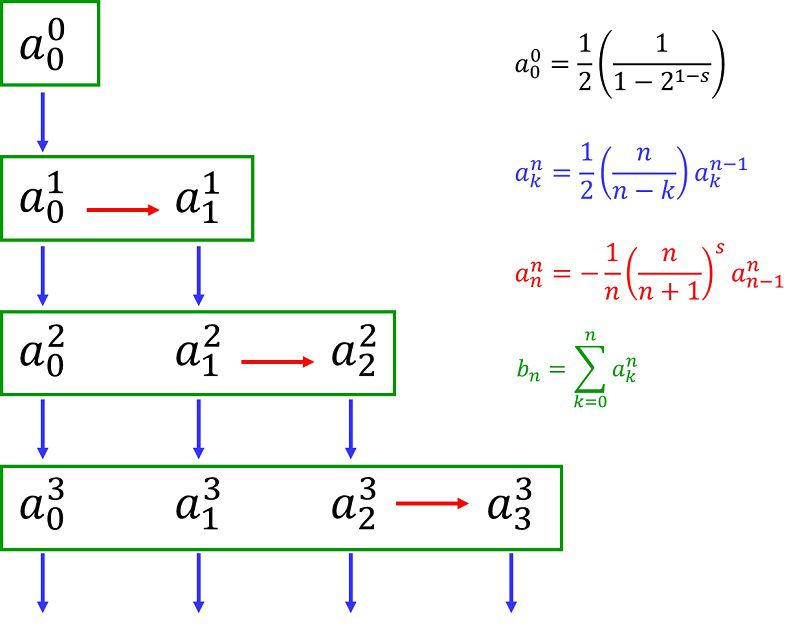
としていけばよいでしょう。
計算量を考えて赤の手順を少なくするようにしています。

fortran90によるプログラム

本当のゼータ関数の値との相対誤差\(\delta\)は約
\(\delta\lt 3\times 10^{-14} (Re(s)\lt 1)\),
\(\delta\lt 3\times 10^{-15} (1 \lt Re(s)) \)
負の領域の方が精度が悪いのは、相反公式から来ています。
相反公式のみを4倍精度演算で行えば
\(\delta\lt 7\times 10^{-15} (Re(s) \lt 1) \)
にまで精度が上がります。目立って精度はあがりません。

2017/01/12に大幅な更新をしました。
以前のものと比べ変更点は、
・4倍精度を使用していない
・計算速度は以前の54倍
になっているので、以前のものを使っている方は更新することを推奨します。
ガンマ関数に関しては複素ガンマ関数の数値計算をご参照ください。

ifort version 16.0.2 20160204, 12.1.0 20110811
gfortran version 4.8.4
で動くことを確かめています。

こちらに4倍精度用のゼータ関数のコードを置いておきます。
精度は何点かで試しましたが、30~32桁一致するくらいです。

ゼータ関数のデータ

計算結果のデータも置いておきます。
(11MB)riemanndata.tar.gz
(9MB)riemanndata.zip
それぞれ、中に
“riemannzeta_high_resolution.txt”
“riemannzeta_low_resolution.txt”
が入っています。
highの方は1列目から4列目にかけて
\({\rm Re}(s):[-20\sim 20],{\rm Im}(s):[-50\sim 50],{\rm Re}(\zeta(s)),{\rm Im}(\zeta(s))\)、0.1ずつ、小数点以下13桁で出力したもので、
lowの方は1列目から4列目にかけて
\({\rm Re}(s):[-20\sim 20],{\rm Im}(s):[-50\sim 50],{\rm Re}(\zeta(s)),{\rm Im}(\zeta(s))\)、0.2ずつ、小数点以下5桁で出力したものです。

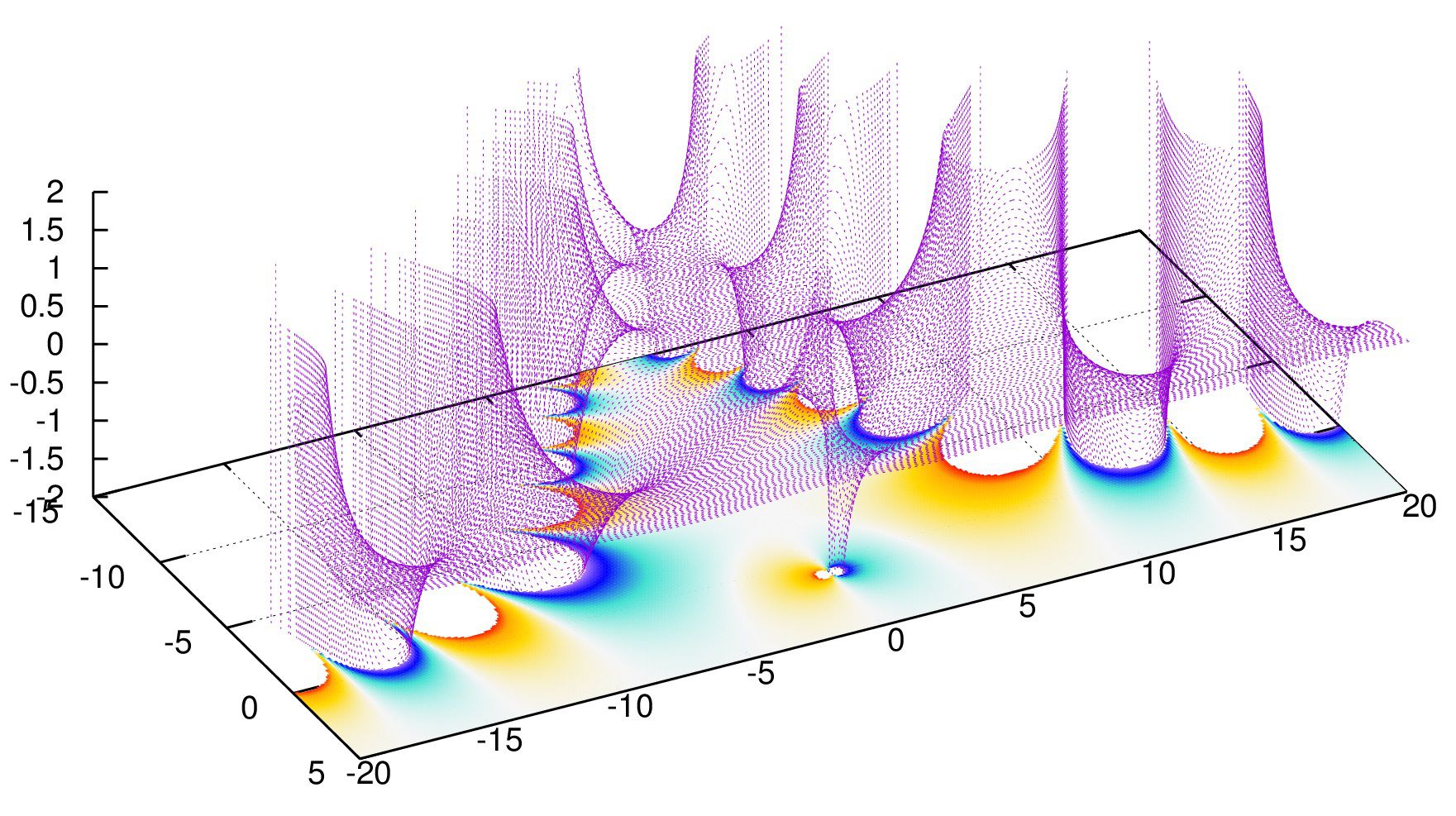
x,y,z軸を\({\rm Re}(s),{\rm Im}(s),{\rm Re}(\zeta(s))\)にとりグラフにすると、

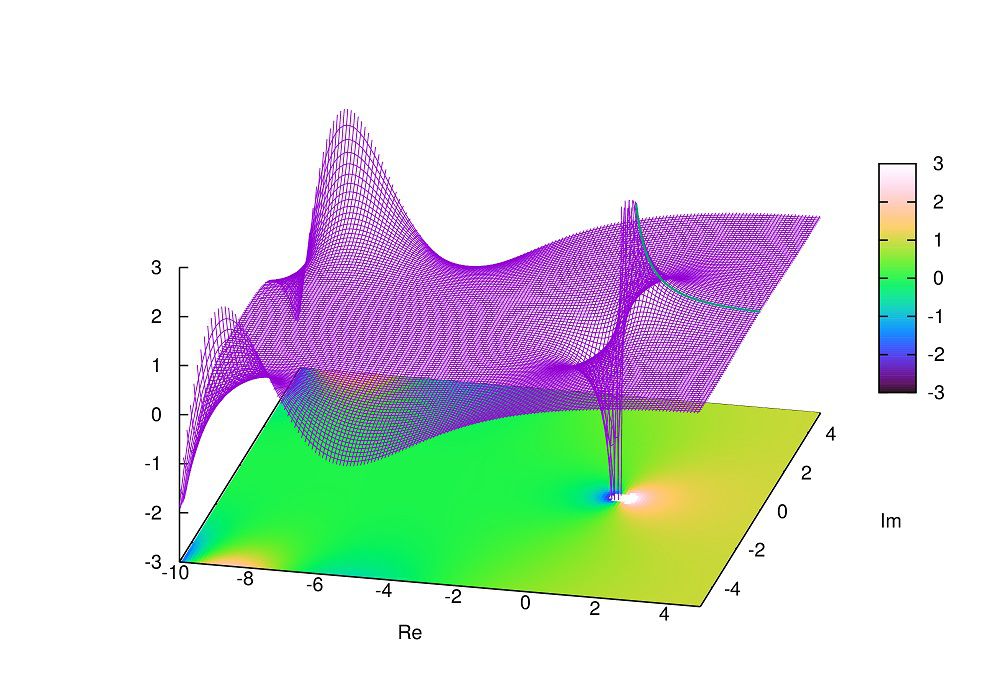
というグラフが得られます。

\({\rm Re}(s)\)が負で\({\rm Im}(s)\)が小さいところで発散が起こるようですので、注意をして使ってください。
何故倍精度でおかしい問題が起こっていたのか？今回の場合はオーバーフローでもなく、アンダーフローでもありません。
原因は桁落ちです。和と差によって激しく桁落ちしてしまうのです。

また、倍精度よりも計算が早いです。なぜならば目標精度までスムーズに収束してくれるからです。

相反公式を用いたので上記問題は発生しません。

[adsense1]

ゼータ関数の実部、虚部、絶対値のグラフ

ゼータ関数の実部、虚部、絶対値のグラフは以下の通りになります。

実部\({\rm Re}(\zeta(s))\)

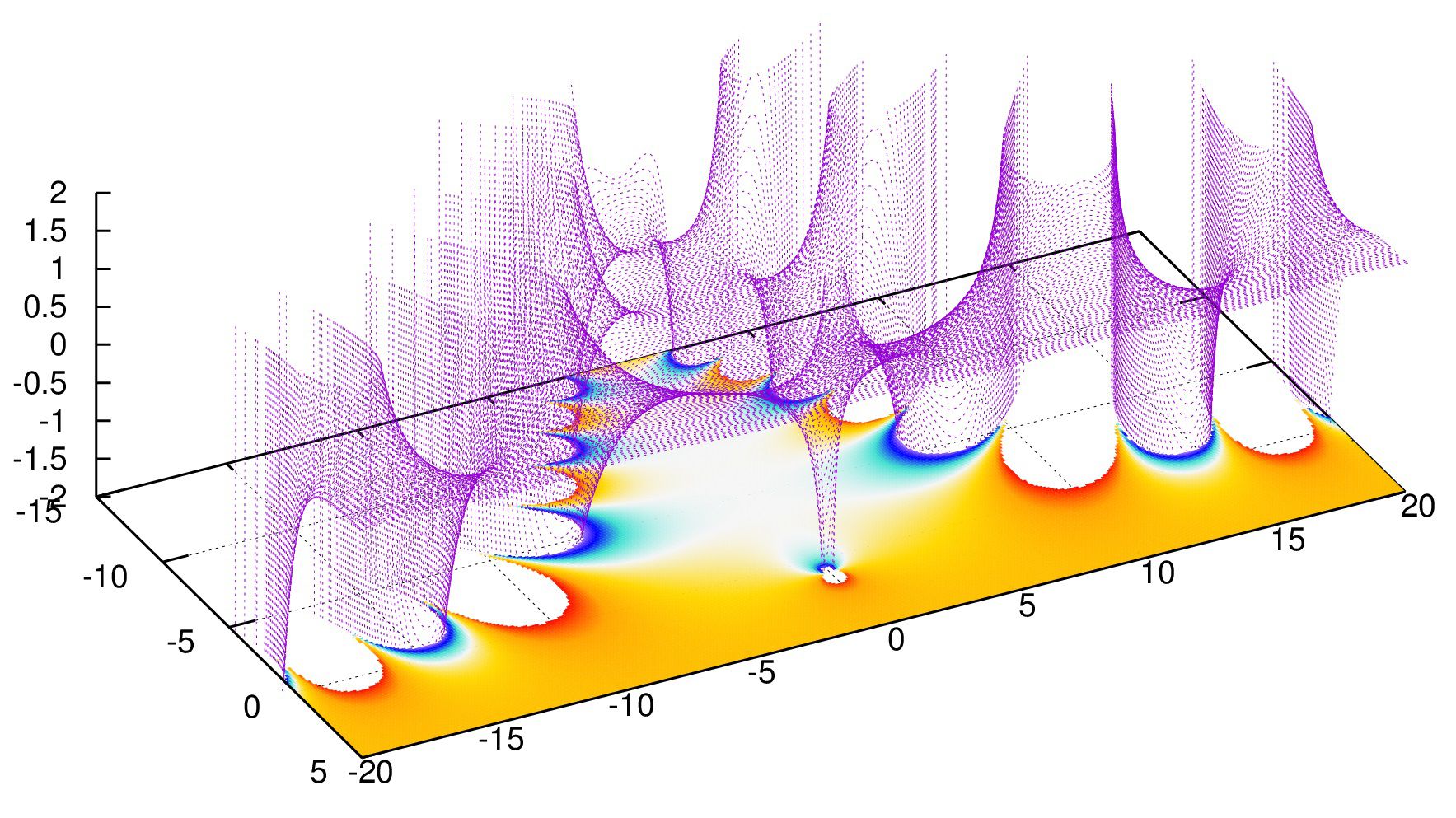
カラーマップ(横軸:\({\rm Re}(s)\),縦軸\(:{\rm Im}(s)\),カラー:\({\rm Re}(\zeta(s))\))

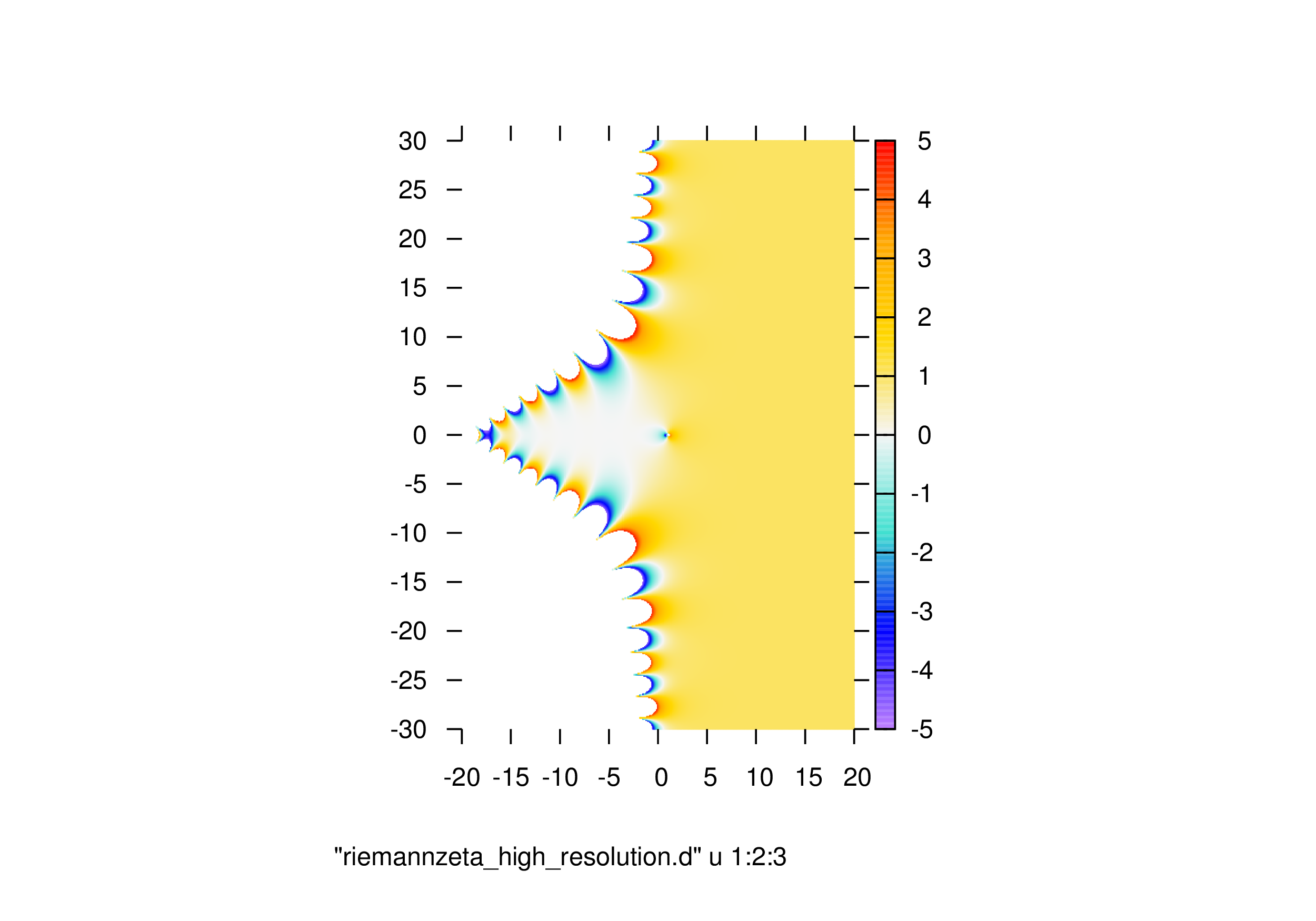
虚数\({\rm Im}(\zeta(s))\)

カラーマップ(横軸:\({\rm Re}(s)\),縦軸\(:{\rm Im}(s)\),カラー:\({\rm Im}(\zeta(s))\))

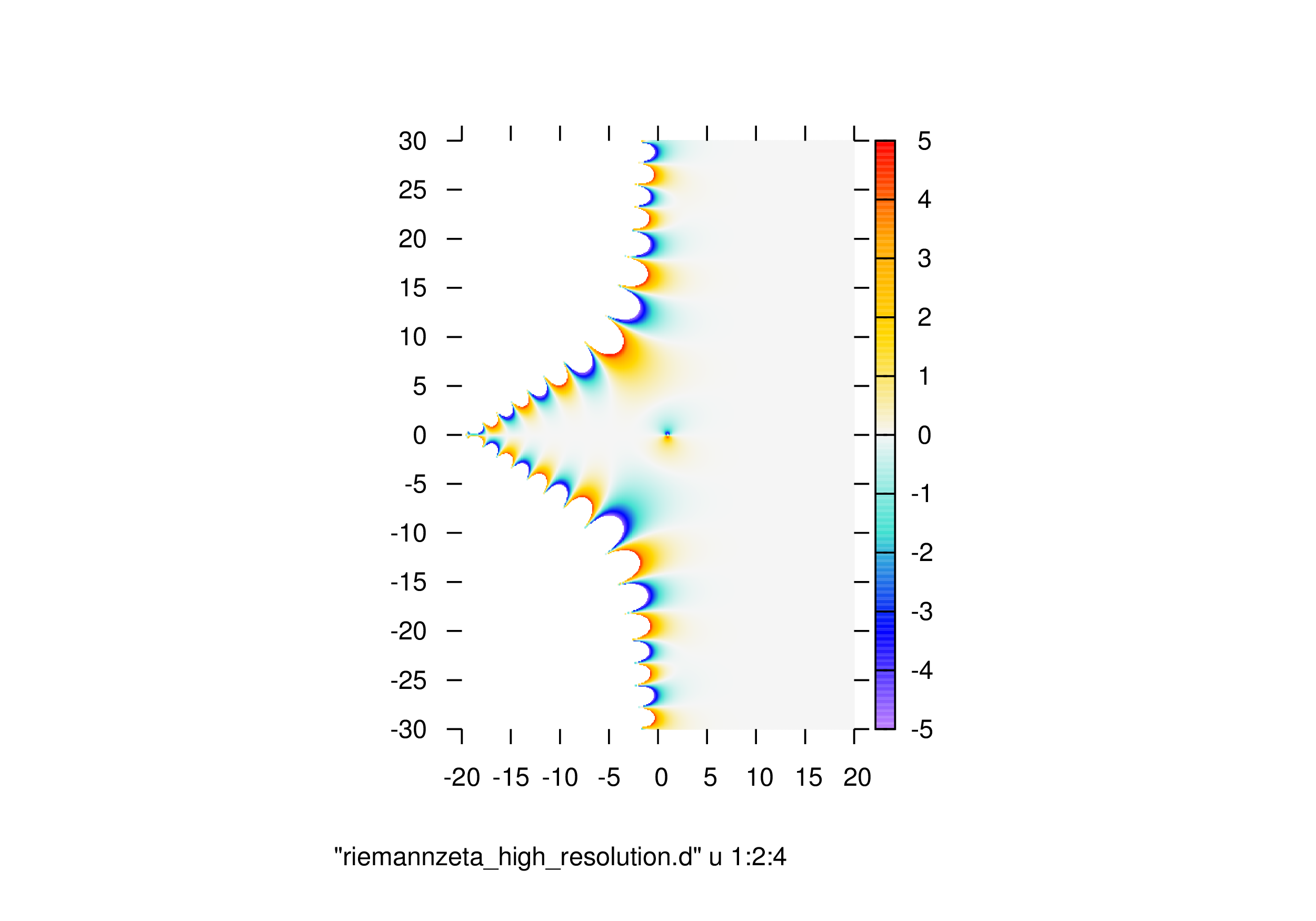
絶対値\(|\zeta(s)|\)

カラーマップ(横軸:\({\rm Im}(s)\),縦軸\(:{\rm Re}(s)\),カラー:\(|\zeta(s)|\))

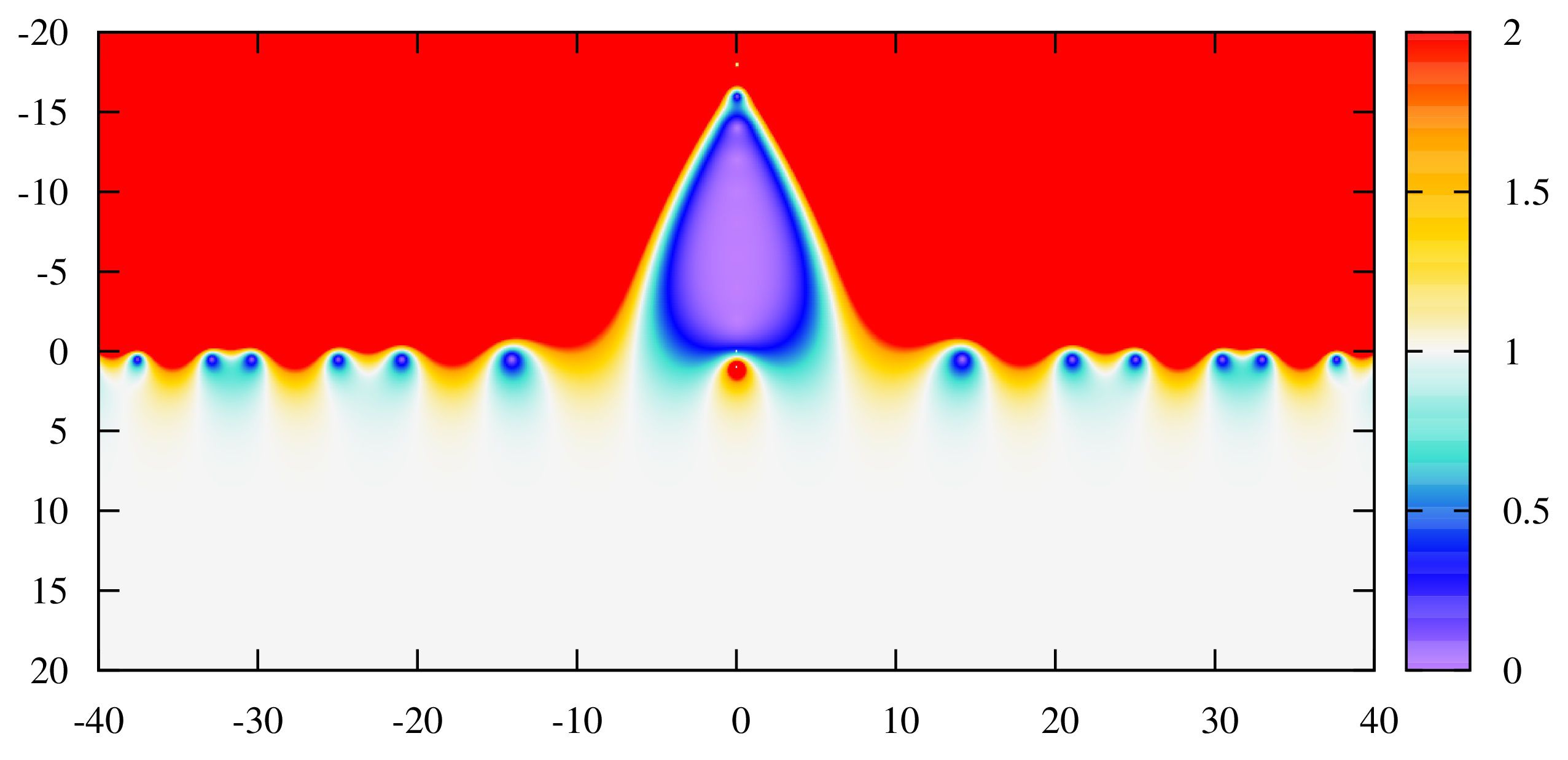
対数プロット(横軸:\({\rm Re}(s)\),縦軸\(:{\rm Im}(s)\),カラー:\((\log{10}(|\zeta(s)|\))

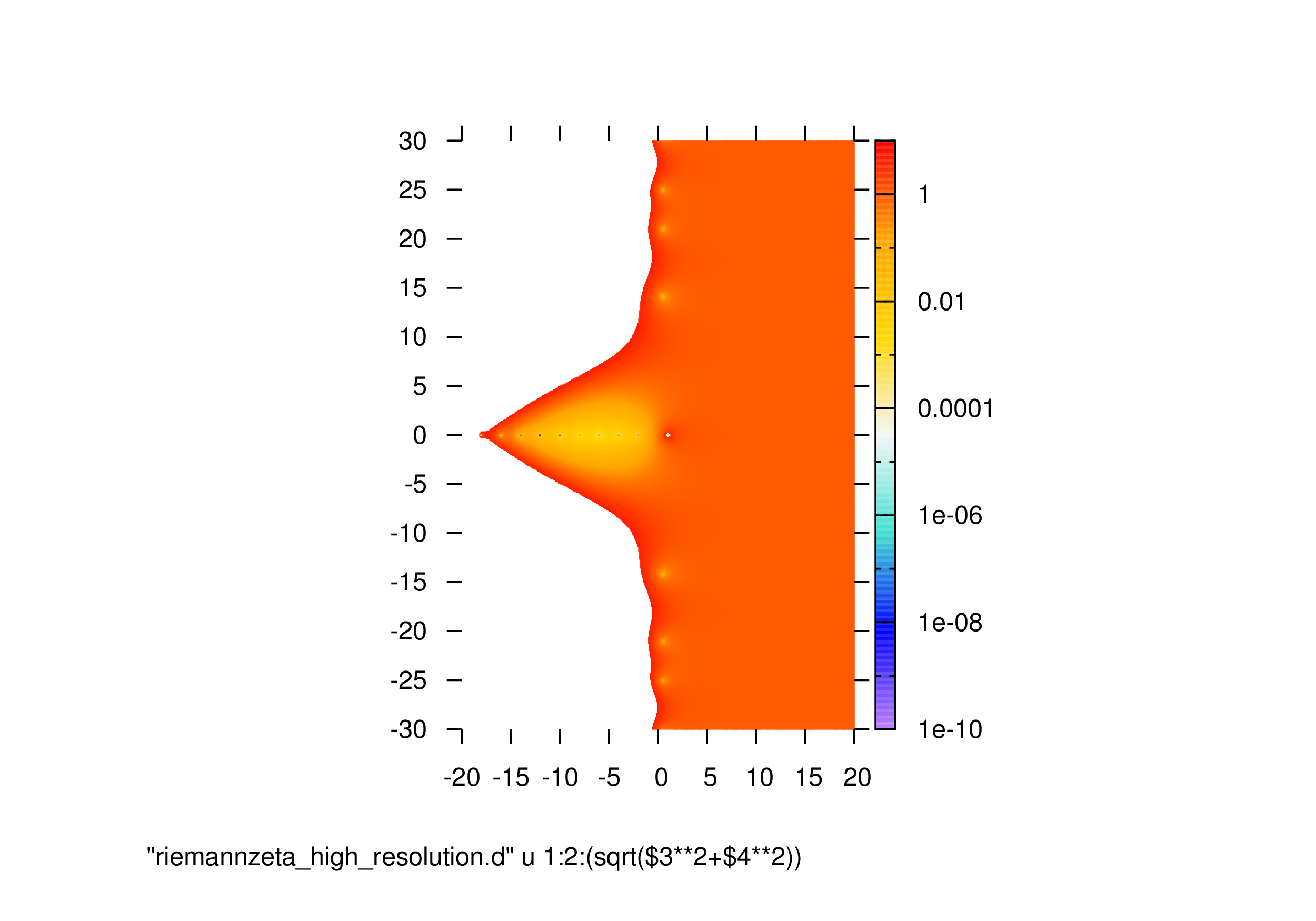
（おまけ）ゼータ関数のニュートン写像(詳しくはリーマンのゼータ関数の複素力学系へ)

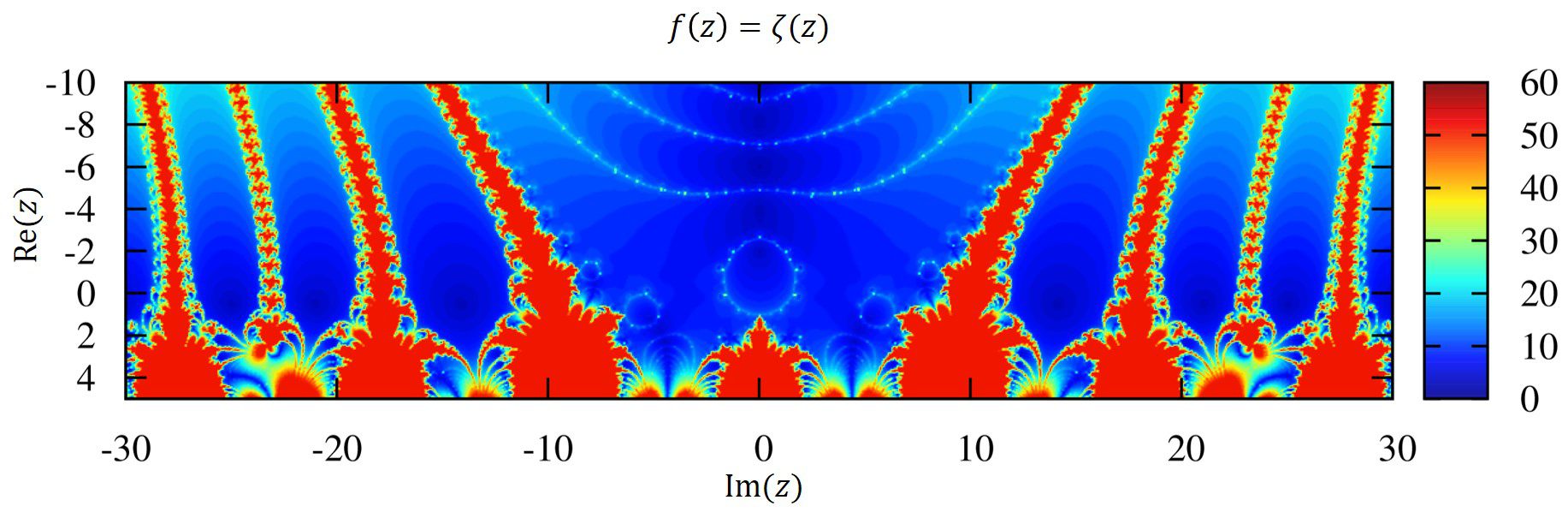
非自明なゼロ点

上記の計算方法(4倍精度のプログラム)で、リーマンの非自明なゼロ点を考えます。
「非自明なゼロ点」はゼータ関数の実数軸上には無いゼロ点のことです。
リーマン予想とは
ゼータ関数\(\zeta(s)\)の「非自明なゼロ点」が\(s=\frac{1}{2}+ix\)(\(x\)は実数)上に全てある
というものです。\(\zeta(s)=0\)が満たされるときはゼータ関数の実部も虚部もゼロになるので、簡単に言えばゼータ関数の絶対値がゼロになる\(|\zeta(s)|=0\)と言うことです。
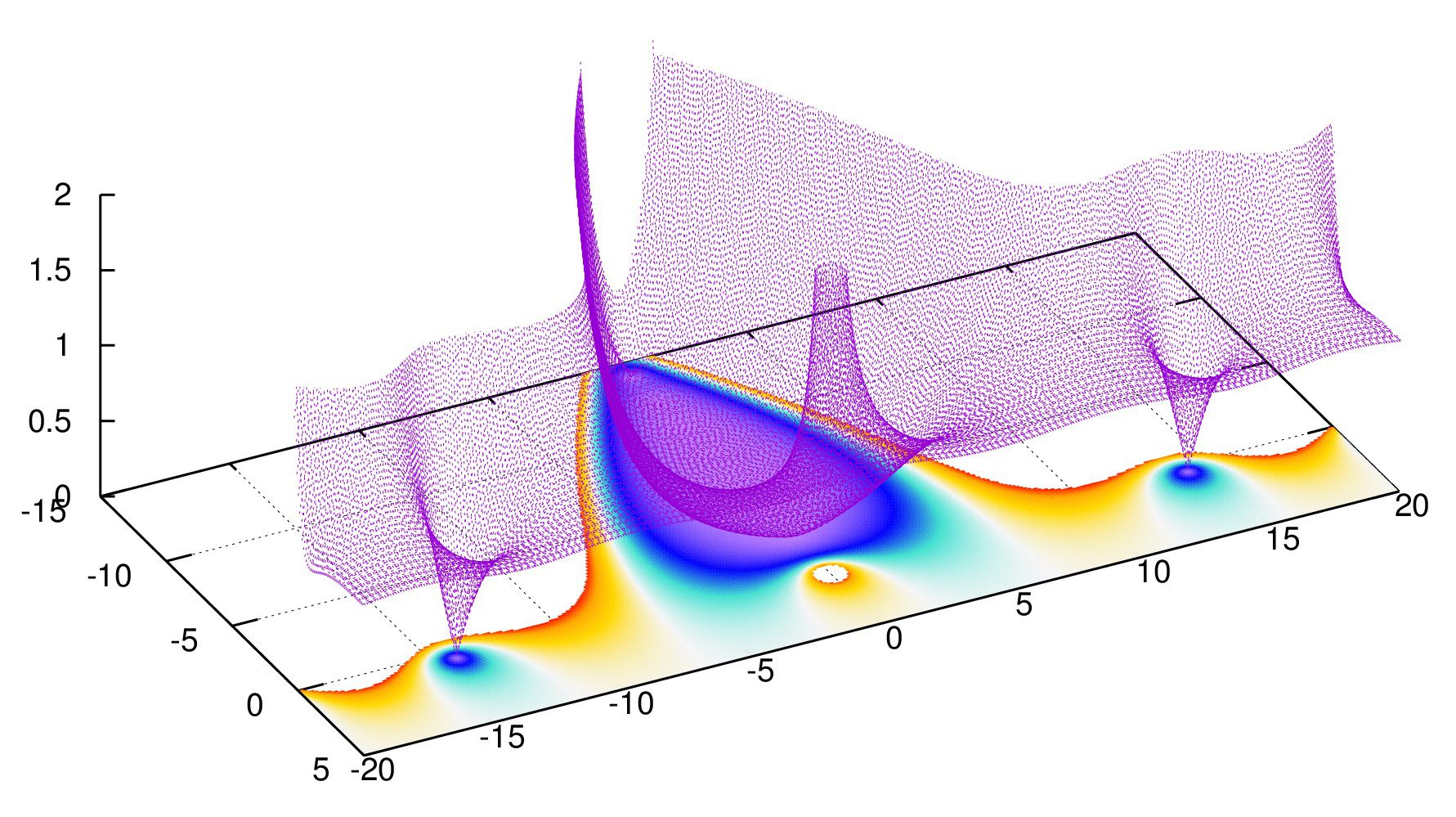
実際に\(|\zeta(s)|\)を可視化してみますとこうなります。

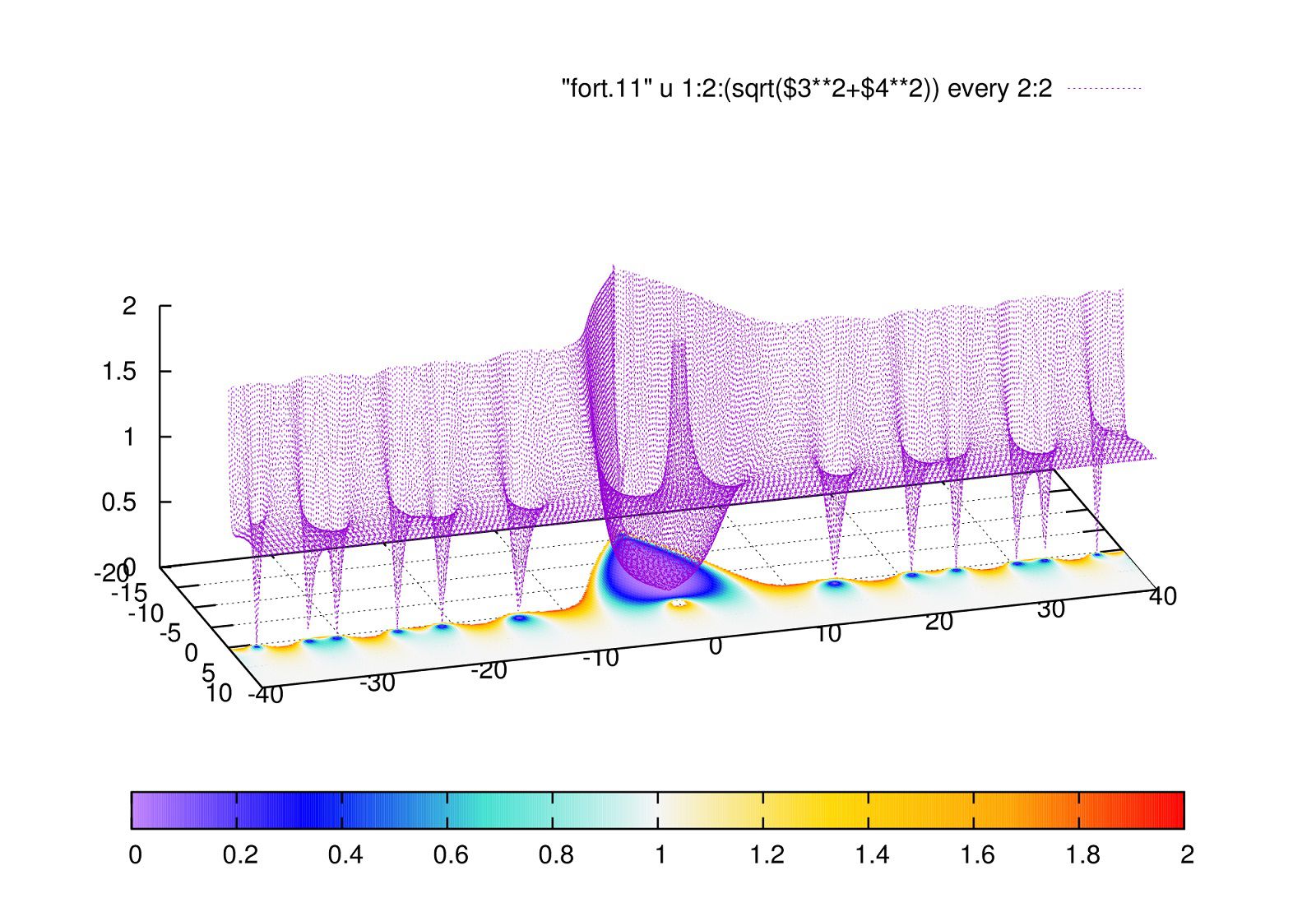
自明なゼロ点

僕は他のページでは自明な点に関する図を見たことがありません。非常に小さいからでしょう。
小さいものを見るには対数スケールで見るのが良いです。実際に書かせてみます。

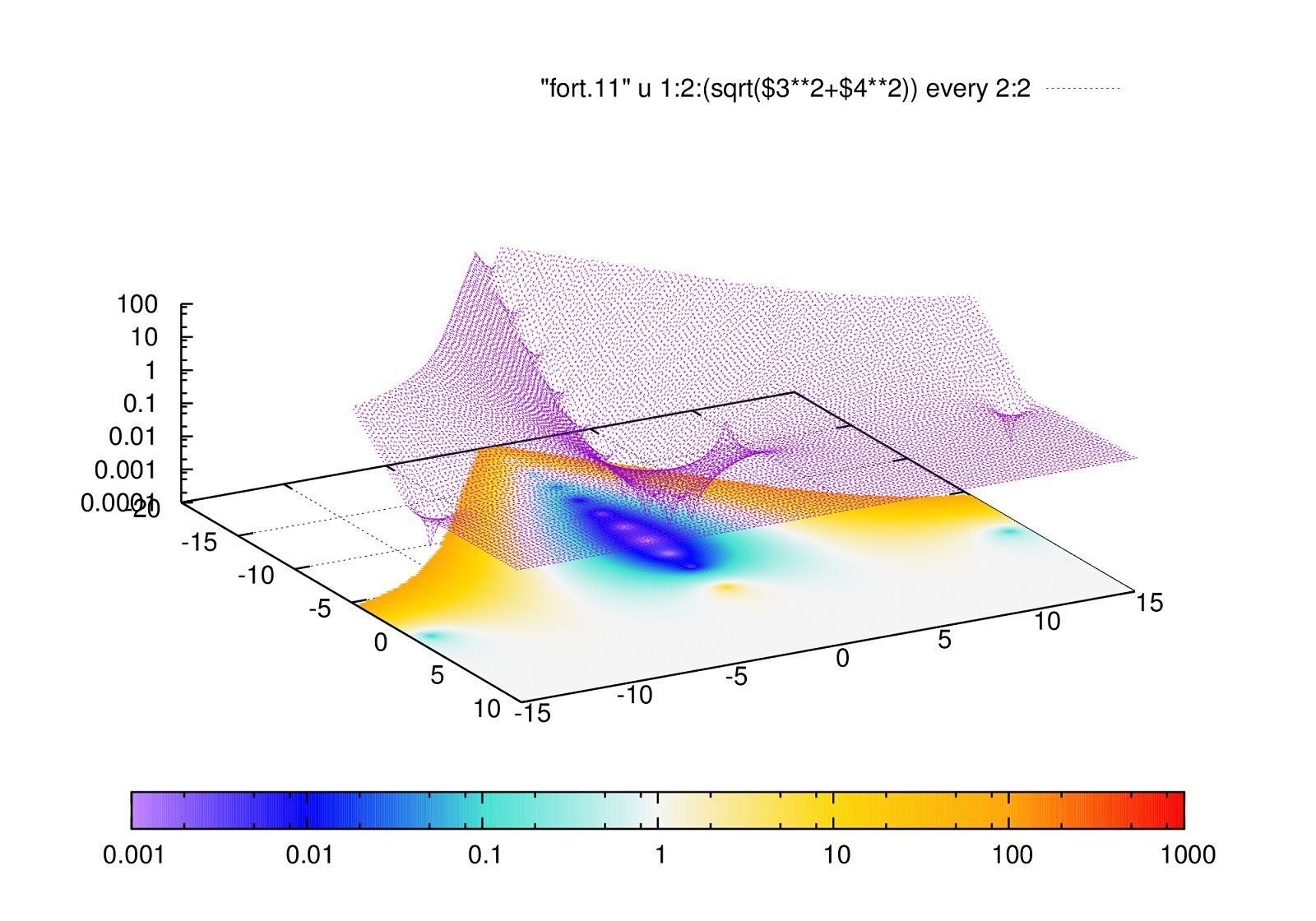
確かに小さいですね。対数にしないと明らかに見えません。

絶対値\(|\zeta(s)|\)を上の図のように表示させるgnuplotスクリプトはこちら。

[adsense2]

クリティカルライン上での計算

クリティカルラインとは
\(
\displaystyle s=\frac{1}{2}+ix
\)
の線です。リーマン予想は、非自明なゼロ点が全てこの上にあるか？という問いかけであり、この計算と繋がっています。

倍精度型のアルゴリズム(zeta)では、\(x\sim 400\)程度まで計算することが出来ます。
これは、

相反公式の
\(
\displaystyle \sin(\frac{\pi}{2}s)
\)
の値がオーバーフローを起こすためです。

倍精度演算では約\(10^{306}\)まで扱えるので、
\(
s=\sin^{-1}(10^{306})\frac{2}{\pi}\sim 1+i449
\)
4倍精度では約\(10^{4932}\)まで扱えるので、
\(
s=\sin^{-1}(10^{4932})\frac{2}{\pi}\sim 1+i7230
\)
となります。
しかし、実際に計算してみると倍精度では確かに\(x=450\)程度まで計算可能ですが、4倍精度では\(x=1600\)程度までしか正しい値を返してくれません。どこかで何かが起こっているはずですが、解析はしてません。

実際に試してみますと、
倍精度では

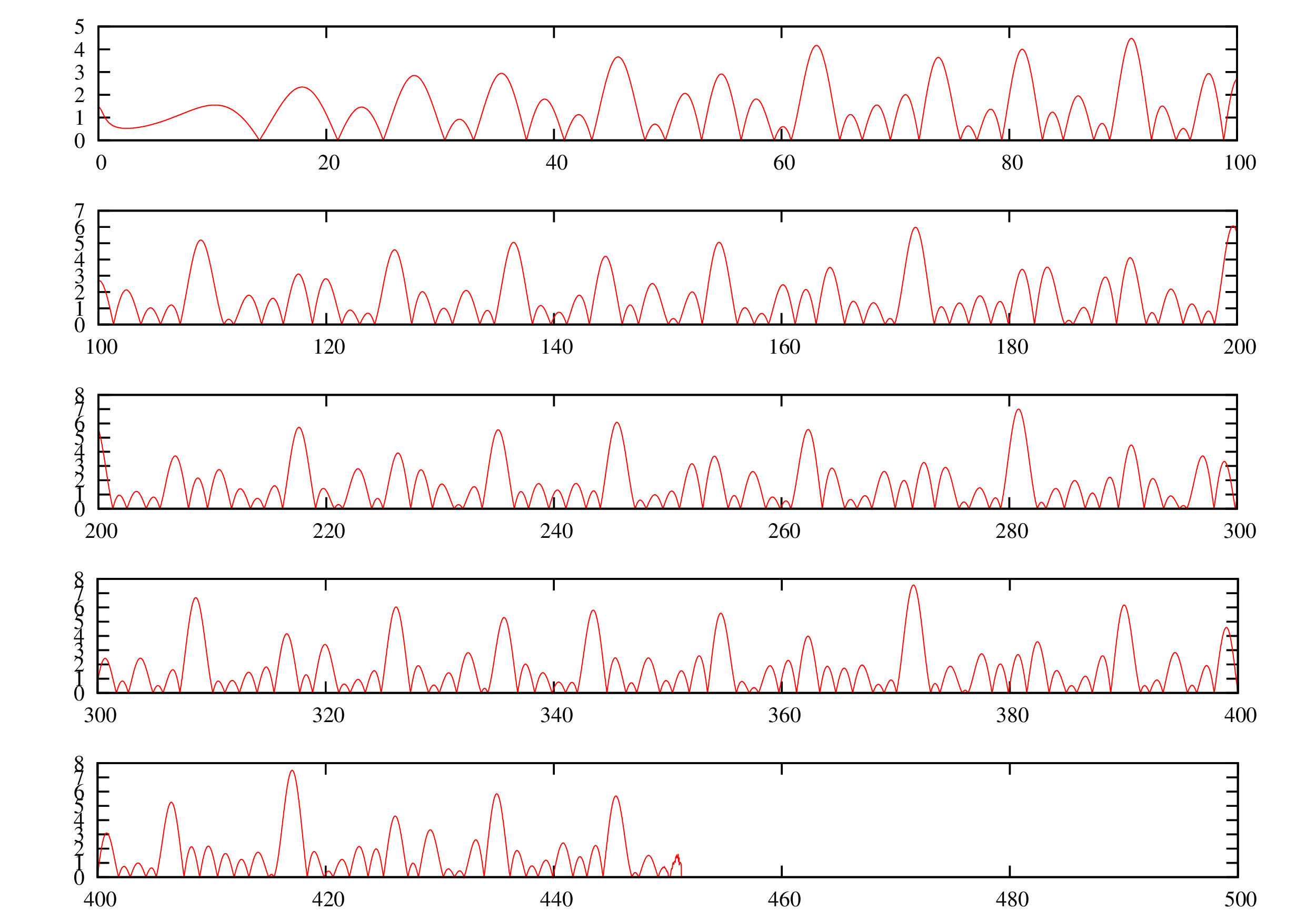
となります。

ゼータ関数の導関数とプログラム

ゼータ関数の導関数も求めましょう。
導関数はゼータ関数の式をそのまま微分すればいいです。なぜなら、正則関数として解析接続されているからです。
実際に微分しますと、
\(
\displaystyle
\zeta'(s)=\frac{1}{(2^s-2)^2}\sum_{n=0}^{\infty} \frac{1}{2^{n+1}} \sum_{k=0}^{n} {n \choose k} \frac{(-1)^k}{(k+1)^s}
\left[ -2^s \{(2^s-2)\ln(k+1)+\ln4\} \right]
\)
変形して以下のように
\(
\begin{align}
\zeta'(s) &=\sum_{n=0}^{\infty} b_n \\
b_n &= \sum_{k=0}^{n}a_k^n \\
a_k^n &= (-1)^k {n \choose k} \left[ \frac{-2^s (k+1)^{-s}\{(2^s-2)\ln(k+1)+\ln4\}}{(2^s-2)^2} \right]
\end{align}
\)
となります。同じように漸化式を求めてやれば、
\(
\begin{align}
a_k^n&=\frac{1}{2}\left(\frac{n}{n-k}\right)a_{k}^{n-1} \\
a_k^n&=-\frac{k-n-1}{k}\left(\frac{k}{k+1}\right)^s\frac{(2^s-2)\ln(k+1)+\ln 4}{(2^s-2)\ln(k)+\ln 4} a_{k-1}^n \\
a_0^0&=\frac{1}{2}\frac{-2^s \ln 4}{(2^s-2)^2}
\end{align}
\)

として求められます。
実際の数値計算では、2番目の漸化式は余り有能ではないかもしれません。
ゼータ関数を求めるときと同じようにやるならば、必要なのは\(a_n^n\)を\(a_{n-1}^n\)から求める作業です。漸化式を用いても直接求めても計算量はさほど変わらない気がします。

導関数の相反公式

相反公式ももちろん存在します[3]。
解析接続されているので、元の相反公式の左辺、右辺をそのまま微分することで求められます。
\(
\begin{align}
-\zeta'(1-s)&=2(2\pi)^{-s}\left\{x\cos\left(\frac{\pi s}{2}\right)+y\sin\left(\frac{\pi s}{2}\right)\right\}\Gamma(s)\zeta(s) \\
&\hspace{3em} +2(2\pi)^{-s}\cos\left(\frac{\pi s}{2}\right)\left\{\Gamma(s)\zeta(s)\right\}’ \\
& x = -\ln(2\pi), \;\; y=-\frac{\pi}{2}
\end{align}
\)

\(
\Gamma'(s)=\Gamma(s)\psi(s)
\)
ここで\(\psi(z)\)はディガンマ関数

確かめはwolfram alphaを用いて以下のコマンドで行いました。
ReplaceAll[D[Zeta[x], x], {x -> -6+2i}]

fortran90によるプログラム

fortran90によるプログラムはこんな感じになるかと思います。
相反公式で、ゼータ関数、倍精度ガンマ関数とディガンマ関数を用います。
ゼータ関数は上の、倍精度ガンマ関数とディガンマ関数はつけておきました。詳しくはディガンマ関数の数値計算をご覧ください。
ここに記述しているのは倍精度のみです。

注釈

他のページでの例えば
リーマンのゼータ関数で遊び倒そう (Ruby編)
等では、漸化式を使わないで直接計算しています。このため、余り項の数\(n\)の数を増やす事が出来ないこと、倍精度と思われるため、桁落ちの問題が回避できない問題が起こります。
実際、私も直接計算するコードをfortran90で書きましたが、項の数を増やせず収束しない事、また計算時間が2~3倍余計にかかります。

参考文献
Riemann Zeta Function — from Wolfram MathWorld, Eq.(21)
draw a horizontal gradient somewhere at the bottom of the graph. -ColorBox

[3]Tom M. Apóstol “Formulas for Higher Derivatives of the Riemann Zeta Function”, Math. of. Comp vol 44, 169, 1985, pp. 223-232.

[4]Madhava-Gregory-Leibniz級数の収束の加速(収束の加速1)

[5]リーマンゼータ関数の級数表示による解析接続 インテジャーズ