LinuxOSの場合です。
ffmpegを使ってaviからgifアニメーションを作る場合のコマンドです。
ffmpegのインストール手順はCompile FFmpeg on Ubuntu, Debian, or Mintここ。
オリジナルのまま、aviからgifに変換したい場合
サイズを800×400にしてgifで出力させたい場合
LinuxOSの場合です。
ffmpegを使ってaviからgifアニメーションを作る場合のコマンドです。
ffmpegのインストール手順はCompile FFmpeg on Ubuntu, Debian, or Mintここ。
オリジナルのまま、aviからgifに変換したい場合
サイズを800×400にしてgifで出力させたい場合
弾道計算(BB弾)の数値計算結果を中心にまとめます。
目次
弾道計算に関するその他ページ
弾道計算(BB弾)の理論
BB弾の回転量について(実験との比較)
弾道計算(BB弾)の結果←今ここ
弾道計算の結果2, 比較と詳細データ
弾道計算(BB弾)のコード(fortran90)
弾道計算のコード(Excel)
バレル内部でのBB弾の方程式
水中下でのBB弾の弾道計算
屋外で行われるサバイバルゲームで優位に立つために、BB弾は重い球が良いのか、軽い球が良いのかを数値計算によって,良い軌道を描く弾道の軌道のパラメータを探索して、現実で調節するための方法を模索します。
サバゲーを行うにあたり、風があったり、遠くを狙う必要のある屋外では
BB弾は重い方が良い
という結論が得られました。
BB弾は重ければ重いほどまっすぐ、遠くまで飛ぶ。また、当たった時に判定がされやすい事になります。
屋内などの風が無く、接近戦(30m以内)が主になる場合ではほぼ差は見られないため、お値段的に軽い球を使うのがいいと思います。
「0.20gのほうが着弾が早い」
→ほとんど嘘
初速は確かに0.20gのほうが早いですが、最大でも15mの地点で0.01秒程度の違いしかありません。30m以上では0.25gのほうが早く着弾します。
「0.25gはまっすぐ飛ぶ」
→本当
→風の影響を受けにくいため、横にぶれにくいだけでなく、縦にもぶれが少くなります。
「0.20gのほうが遠くに飛ぶ」
→嘘
→0.25gのほうが遠くまで飛びます。
「0.25gのほうがヒットを取りやすい」
→本当
→弾の持つエネルギーは0.25gの方がどの地点でも大きくなるため、当たった時に判定されやすいことになります。
まとめると、
0.20gが優れているのは値段だけ
ということになります。
[adsense1]
以下、詳細なデータを載せます。
ニュートン力学の範囲内で計算します。
考慮した力と条件は、
です。コリオリ力は重力に比べ3桁程度小さい力なので考慮に入れていません。
空気の粘性率は、空気の密度は気温20度、乾燥した空気中のものを使用しています。
僕が調べた範囲で他のページではBB弾の回転の減衰が考慮されていませんでした。本稿ではそれを考慮したことが一つの特徴です。
運動方程式の導出や、理論に関してはこちらの弾道計算(BB弾)の理論をご覧ください。
計算が実測のデータと合っているのかをまず初めに検証します。
東京マルイ G36CにおけるノーマルホップとG-HOPの弾道特性の実測データと、本稿の数値計算結果との比較を行います。
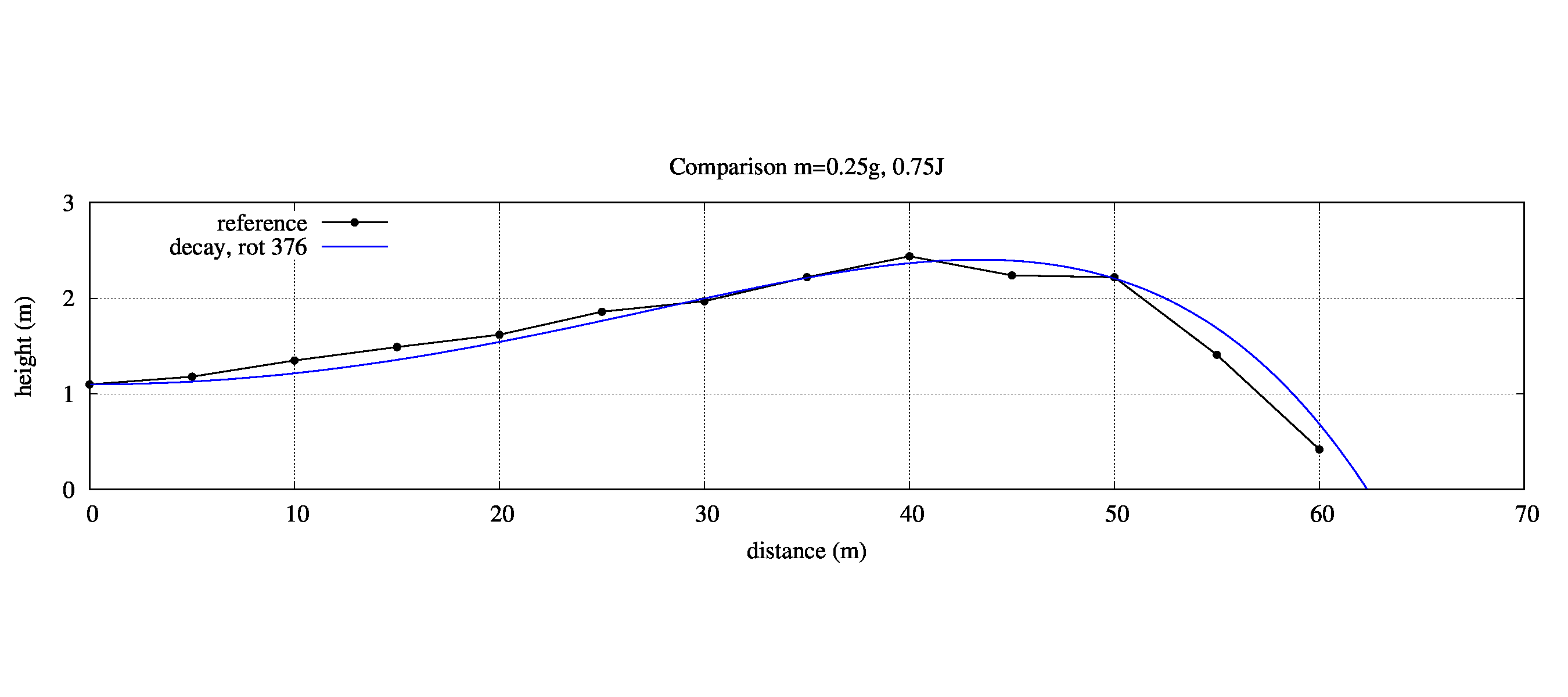
青線、実測結果は黒の点と線です。
※実測データにおいて、BB弾の回転数は測定されていなかったため(難しいため)、最高到達高さが2.4mになるように数値計算の回転数を決めました。
全体的に非常に良い一致を見せていることが分かるかと思います。50m,60m地点においては10~20cm程度の差しかないのではないでしょうか。この実測データの再現、という点においては十分に信頼できる数値計算結果になっていると思います。
ただし、打ち出し直後の浮き上がり具合に若干の差があります。
このずれの原因として、実測データの高低さの加味が十分ではないか、射出角度が若干違う、ということが考えられます。
実測時ではなく、改めて高低差を加味した、と実測データのページにあるので、場所が完全に同じではないかもしれないと考えられます。
風で揺らいでいる、ということは無いでしょう。もしも風で揺らいでいるとしたら、遠くで差が出るはずです。射出直後でこれだけ揺らいで遠くで揺らがないというのは納得ができません。
本稿の数値計算は実測データと十分に一致している、と確認したうえで、いろいろとパラメータを変えて計算してみました。
まず、一番気になるBB弾の軌道を見ます。
エネルギーを0.90Jで固定して、パラメータを様々に変え0.20gと0.25gのBB弾で比較してみます。
その結果がこちらです。赤文字が0.20g, 青文字が0.25gであることを意味しています。
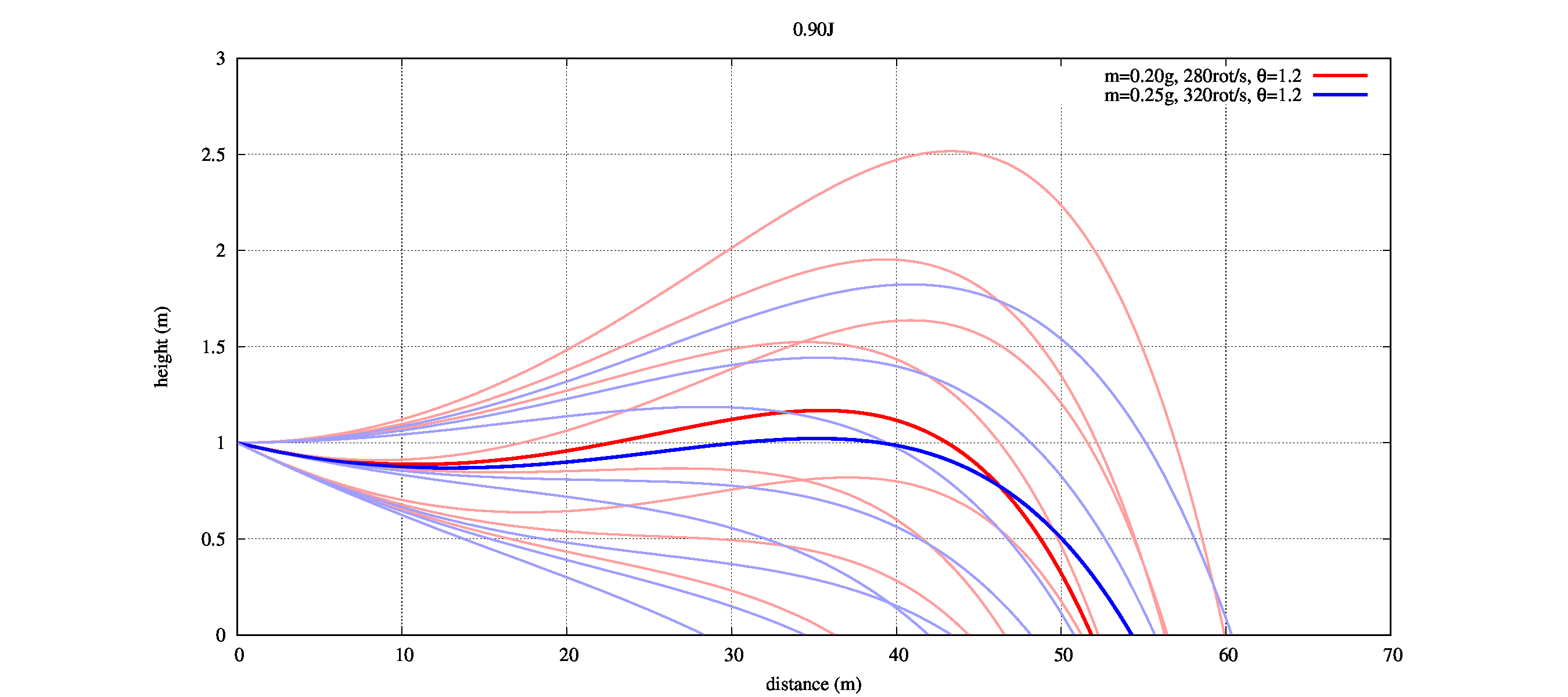
上記グラフは、角度0, 1.2, 2.4°、回転数240, 280, 320回転/秒の組み合わせによる軌道を計算したものです。
BB弾が描く良い軌道とは
軌道であることだ、と考えます。つまり、1つの「最適な軌道」として「上下振れ幅が最小になる軌道」だと言えるでしょう。
上の画像の例でいうならば太線で示した
0.20g → BB弾が280回転/秒で回転し、下向きに1.2°方向に射出されたとき
0.25g → BB弾が320回転/sで回転し、下向きに1.2°方向に射出されたとき
がそれに近い軌道でしょう。
0.25gでこの「良い軌道」に合わせることができたなら、50m先の敵までは、喉~胸あたりに照準を合わせることで確実にヒットが得られるでしょう。
もう少し、この「良い軌道」について調べてみます。
ここでは、重さの違う0.20gと0.25gとを比較するために、ゼロインを50[m]に合わせ、上下方向の振れ幅が最小になる時で比較します。
 ゼロインを50mに合わせた時、0.20gでは60cmの振れ幅、0.25gでは40cm程度の振れ幅になります。
ゼロインを50mに合わせた時、0.20gでは60cmの振れ幅、0.25gでは40cm程度の振れ幅になります。
0.20gよりも0.25gの方が小さい振れ幅です。予想通りといえば予想通りの結果ですね。
次に着弾時刻を見てみましょう。30m地点までは0.20gの方が若干早く着弾し、それ以降は0.25gのほうが早く着弾します。50mの遠距離で比較しますと、0.20gと0.25gとの着弾時刻の差は約0.13秒。まばたき程度の差があります。
ちなみに15mでの着弾の時間差は0.01秒です。とても微々たるもので、この差は認識できないと思われます。よって着弾時刻も上下の振れ幅も少ない、遠距離にも対応できる0.25gを使うのがいいでしょう。
また、エネルギーは発射した瞬間から着弾するまで、どこでも0.25gの方が高いため、遠くでも判定がされやすいことになります。
遠距離を狙いたい場合は着弾速度、上下振れ幅に影響するだけでなく、判定もされやすい重い球を使いましょう。
2016/03/13
計算コードを変更し、動画化しました。点の間隔は0.04秒で、gifアニメの速度の時間間隔と実際の時間間隔は同じにしてあります(すなわち、gifアニメの1秒と現実の1秒が同じ)。
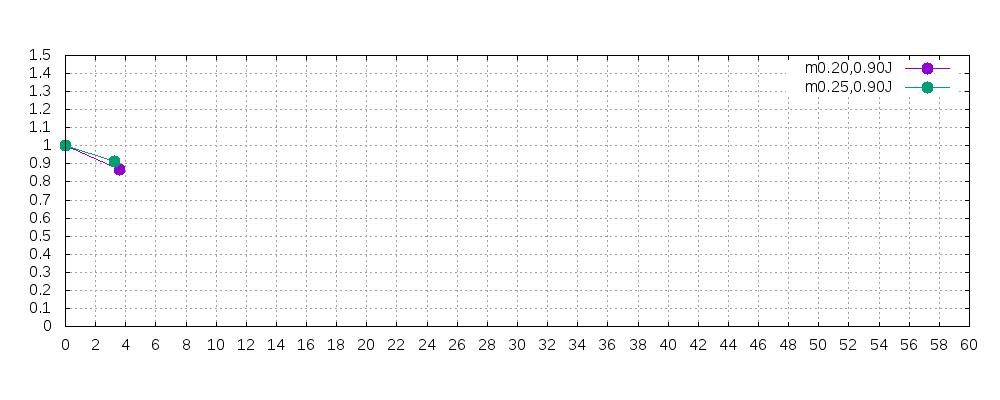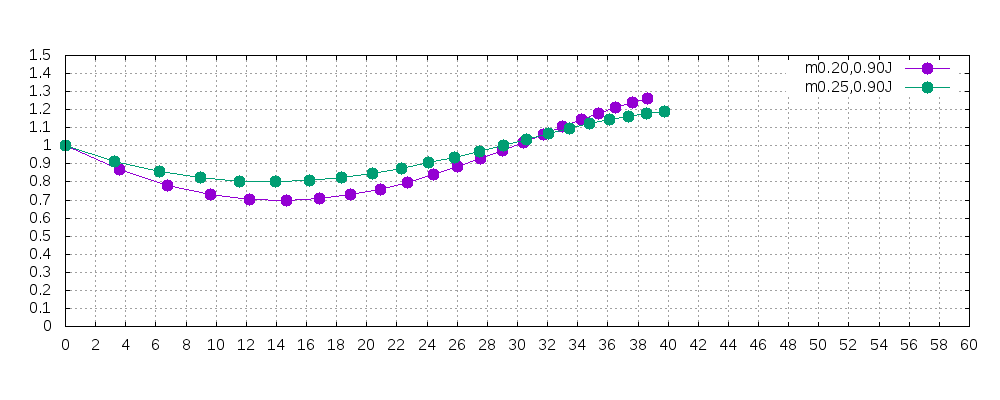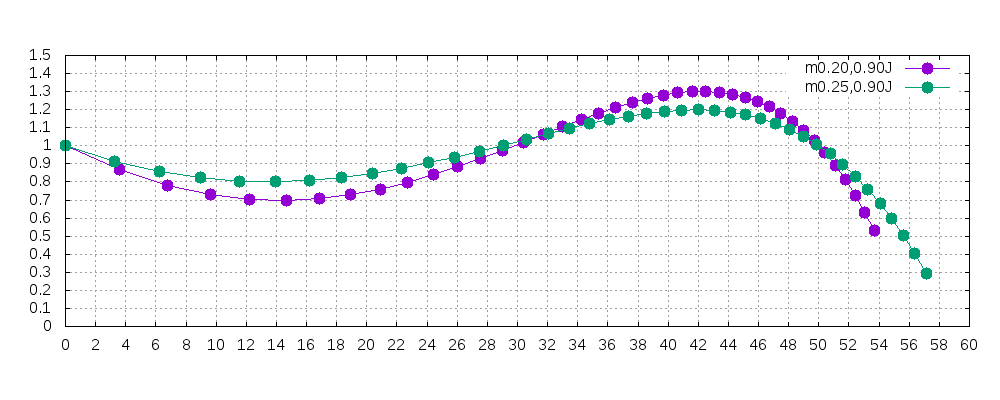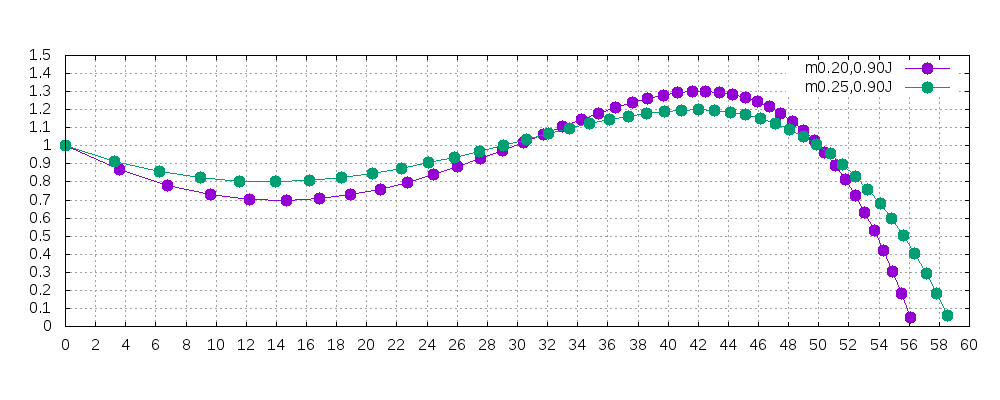
こちらは静止画。
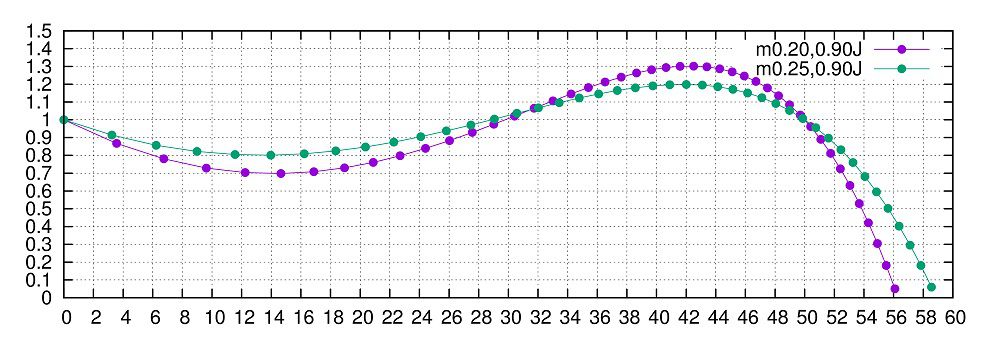
さて、上下方向の振れ幅を最小限に抑えながらゼロインを適当な位置に合わせたい場合について考えます。
遠くにゼロインを合わせたい時、飛ばせばと飛ばすほどホップを強くかけなければなりません。その結果、上にも下にもブレることになります。
この関係性がどうなっているかを調べますと、以下のようになります。
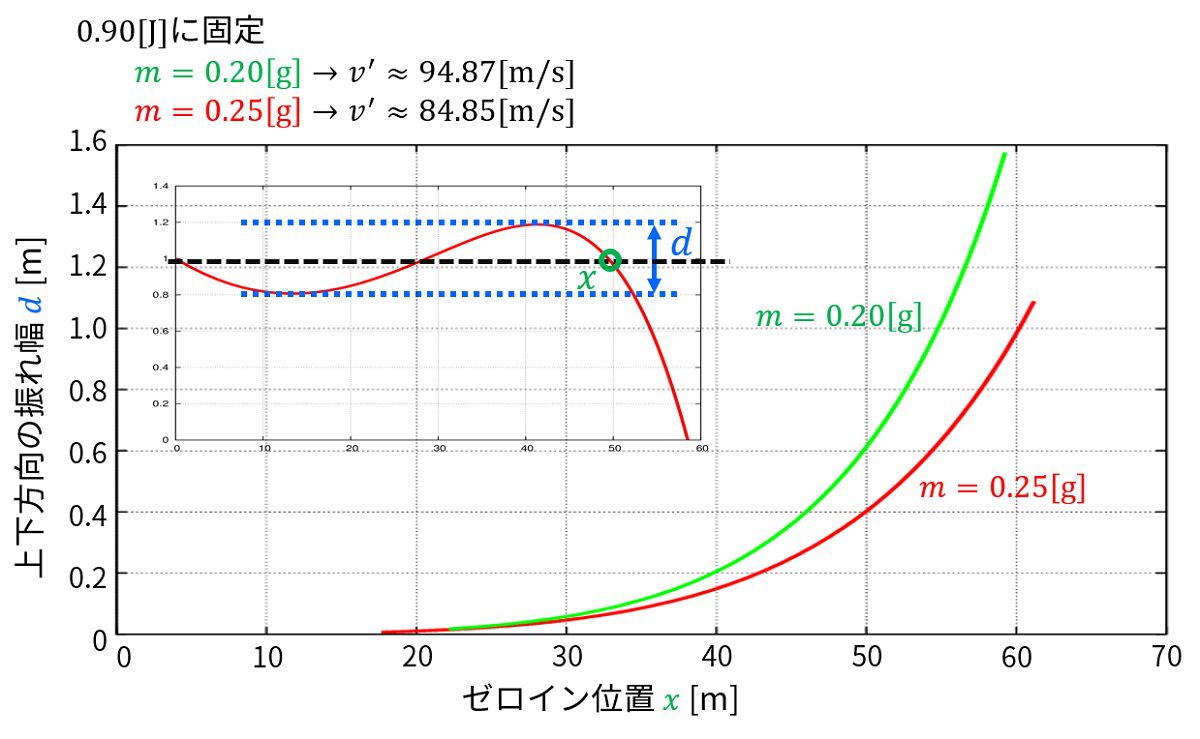
エネルギー0.9Jの場合で、上下の振れ幅を最小に抑えるパラメータで考えますと、段々と上下方向の振れ幅が大きくなっていることがわかります。
これは空気抵抗によって弾速が減少するためにその分、ホップによって時間を稼がなければならないことに由来します。
例えば、
0.20gのBB弾で50mにゼロインを合わせた時は上下振れ幅が60cm(射出位置から30cm下がり、ホップによって射出位置から30cm上昇し、ゼロインを迎える)ですし、
0.25gのBB弾で50mにゼロインを合わせた時は上下振れ幅が40cm(射出位置から20cm下がり、ホップによって射出位置から20cm上昇し、ゼロインを迎える)です。
この重さの違いによる上下方向の振れ幅は顕著に表れます。
60mなんかにゼロインを合わせようとすると、0.20gでは上下方向に1.6mずれることになり、0.25gでは上下方向に1mずれることになります。
もしかしたら、0.20gで60mに合わせた場合、フィールドで立って撃たない限り、先に地面についてしまってダメになるでしょう。
これらから、遠距離ではますます重いBB弾を使ったほうが良いという結果が得られるわけです。
※ただし、中距離に当てるつもりがない場合はホップをある程度かけて上向きに射出したほうがいいでしょう。
さて、サバゲーに行き、シューティングレンジで調節をすることを考えます。
BB弾の回転数など知っているわけがありません。また、角度1.2°などそんなこと分かるわけがありません。
さらに、BB弾がどこまで飛んだかは大抵の場合は10m単位でしか分かるはずがないのです。
せめてジュール数(弾速)は知っているとします。この状況で良い軌道へ調節することを考えましょう。
ここでは、0.25g, 0.9J(初速84.85[m/s])の場合を考えます。
この場合の手順は、
手順1, 射出する銃口の高さと50m地点にある同じ高さにある的に照準を合わせる。
手順2, ホップ無しで、50m先の的に照準に合わせたままBB弾が地面に落ちた時の位置が、おおよそ
\(10\times(\mbox{射出高さ[m]}) +10[\mathrm{m}]\)
になるように調節する。
手順3, その照準に合わせたまま、徐々にホップを掛けていき、50[m]の的に当たるまでホップを掛けて調節する。
です。
詳しく説明すると、
手順1では角度を決めるための基準点を探しています。
手順2では角度をホップ無しの場合で、到達距離を見ることによって決定します。何点か計算したら、射出する高さと良い角度の時の落下地点は、\(10\times(\mbox{射出高さ[m]}) +10[\mathrm{m}]\)という関係でした。
なので、地面からの銃口の位置が分かれば、良い角度での射出は、到達距離を見れば分かるのです。
※空気抵抗のない場合、\((\mbox{落下距離})\propto \sqrt{射出高さ}\)になります。ただし、短い区間であれば線形補間で良いでしょう。ちゃんと線形補間すると、\(10.40\times(\mbox{射出高さ}[\mathrm{m}])+9.87[\mathrm{m}]\)となるのですが、実用上は簡単な\(10\times(\mbox{射出高さ[m]}) +10[\mathrm{m}]\)で十分でしょう。
手順3では、その照準のまま、だんだんホップを掛けていき、50mに合わせればいいのです。
もう一つ具体例、0.20g, 73m/sの場合を考えます。
これは、僕が持っている電動のmp7a1のなにもカスタムしていない時の値です。
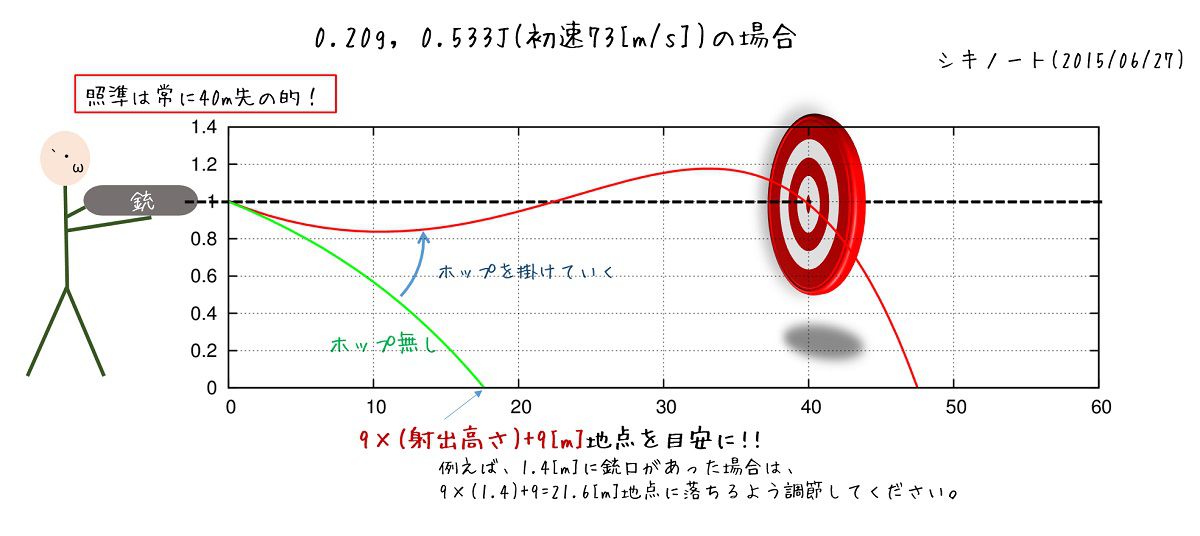
50mに合わせると上に40cm、下に40cmも上下するので、無理に狙わず、40mで合わせています。
(※上のグラフとはエネルギーが異なるため、”ゼロイン距離と上下方向振れ幅との関係”で紹介したグラフとは上下振れ幅が異なっています。)
この時のパラメータは、エネルギー0.533J, 下向きに角度1.81度、回転数42回転/sです。
mp7a1はこちら。
2丁銃を持っている場合、精密射撃用と遠距離用と分けることができます。
30m内では上下方向のブレが6cm程度になるので、近接用と割り切りってしまい、
遠距離では上のパラメータで調節しておけば、どんな距離でも気持ち良く狙えます。
例えば、基本的に上のパラメータで調節した銃を使っておき、相手が隠れた時など、壁の小さい隙間を狙って近距離用で精密射撃を行う、なんてことができるかと思います。
|
|
|
夏場と冬場ではどのくらい弾道が変わるのでしょうか?
0.25g, 0.9Jで、温度10℃、20℃、30℃で撃った時の軌道の違いを考えます。
青が10℃、黒が20℃、赤が30℃です。
基準は20℃です。20℃でゼロイン50mの時の最小の振れ幅に合わせた時に他の温度ではどうなるかを考えます。
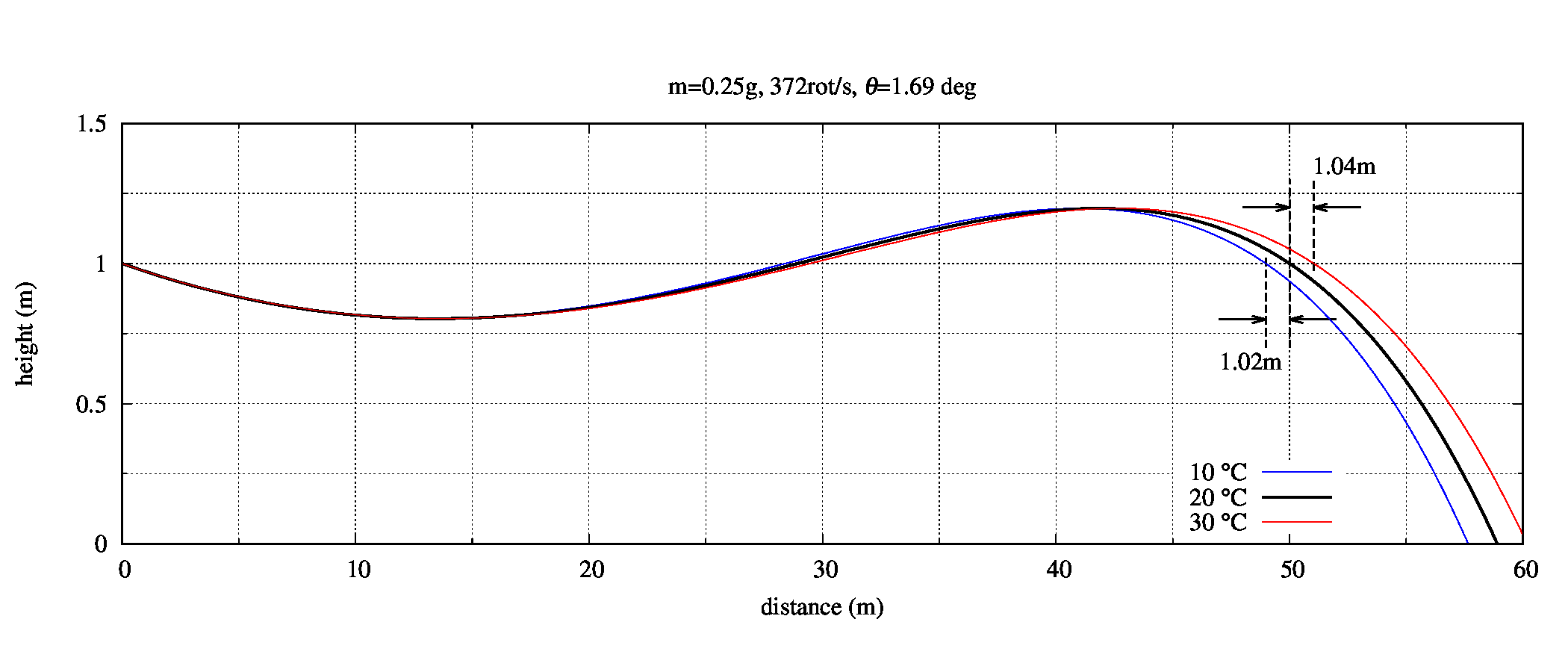
結論として、10℃変わるごとに約1m飛距離が変わります。
なので夏場の方が冬場よりも2m程度よく飛ぶことになります。
弾道計算本の公開から1年経過しました。
発射に至るまでの計算結果に引き続き、少しだけ中身を公開します。
ここで公開するのはBB弾は100m飛ぶのか?という点です。
結論は、
0.90Jで0.30gまでのBB弾では100m飛ぶことは無い
です。
どんなに回転を掛けても飛びません。
下のグラフは、0.90Jで、高さ1.0mから射出した時の着弾点のグラフで、
横軸:回転数、縦軸:射出角度
で表したものです。

枠内の数字は地面に到達するまでの飛距離を等高線で表しています。
現実にエアガンを撃った時に掛けられる回転数は、大きく見積もっても各画像左下の白い点線内です。
ちなみに、最大飛距離を出す射出角度で回転を掛けた場合の弾道は全く現実的ではなく、0.20g(上の画像左上)では、
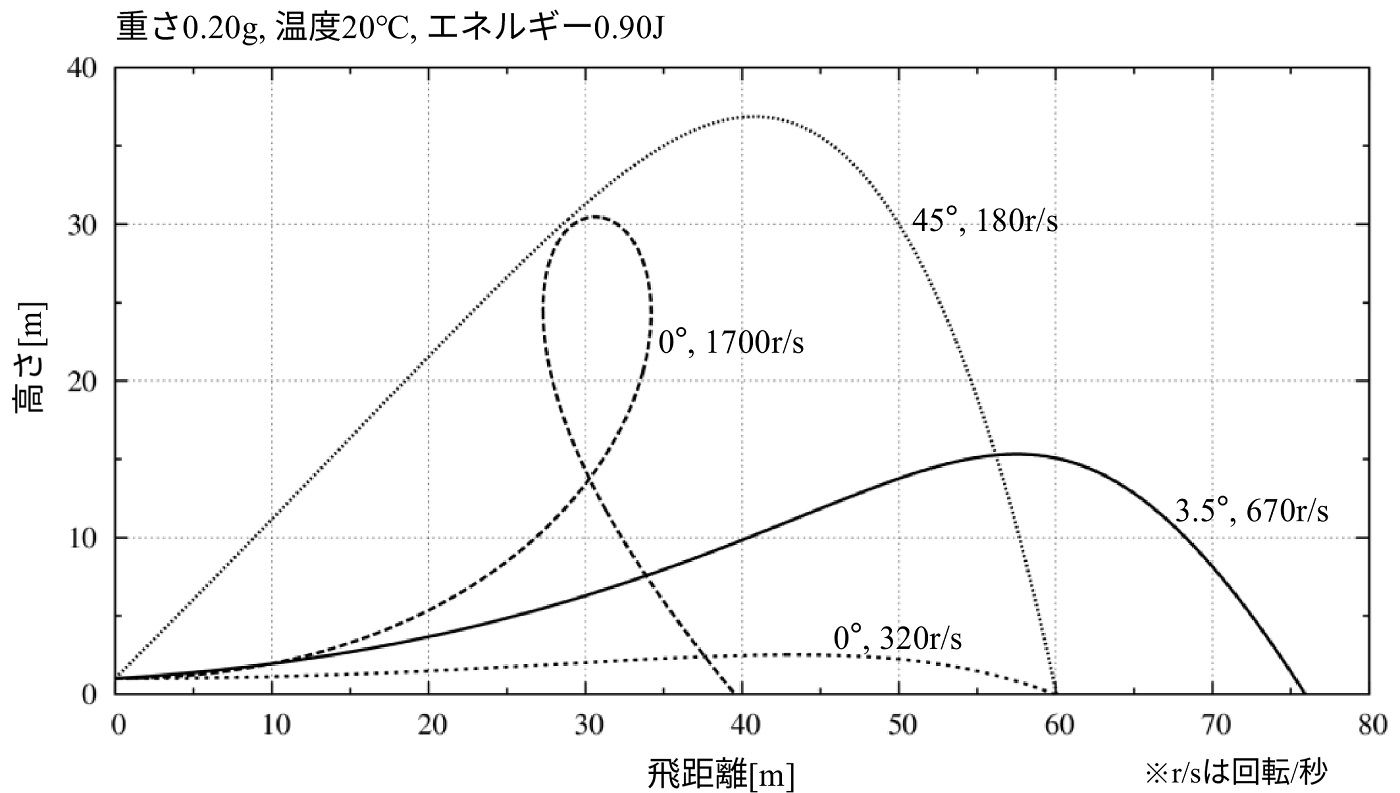
の軌道を描きます。(r/s は 回転/秒を表します。)
2015年12月、内部をカスタムしていないmp7a1でopsに行き、実際に撃ってきて理論通りの軌道になるだろうか、と試してきました。
レーザーサイト、その他もろもろは持っていないので考察ではなく、感想としてみてください。
僕個人の感想をまとめると、
でした。
0.20gと0.25gの差は明らかだと感じました。軌道に対しては体感では少しだけ分かる程度でしたが、集弾性がとにかくいいのです。着弾点でばらけることがほぼ無いのです。実際にどの程度影響していたか分かりませんが、0.20gから0.25gに変えた時、キル数が上がりました。
とても気持ちよく戦えるので、初心者の方を誘ったりする際は是非0.25gを使わせて、サバゲーマーの仲間入りをさせてください。
一度下がってから上がる、これは理論上では一番良い軌道であることは確かなのですが、起伏の激しいフィールドでは、この”一度下がる”が非常に厄介です。一度下がるため、そこに障害物(例えば斜面等越しに当てるとき)があったら当たらないのです。少し上向きに撃とうものなら強ホップのため、敵の頭上を通り越します。
結果、敵から反撃を受け、こちらからは当てられない状況が生まれました。
起伏の激しいフィールドでは、30~35m程度まで数cmの振れ幅でまっすぐに進む軌道が一番良いと思います。
それよりも遠い場合は山なりに何発か撃てばいいので、非常に適していると感じました。
今度は平坦なフィールドで試してみたいと思います。
[adsense2]
@hthsi アイディア提供。実際にサバゲーをやっている上で気になること、○○の違いが知りたい!といったアイディアを弾道計算を行う初期の頃からいっぱいいただきました。重さの違いにありがちな話はほんと?の部分があるといいよね、等の分かりやすい説明は@hthsiの提案です。ありがとうございます!
また、サバゲーるにて告知をしていただきました。
0.25g弾の優位性について
2015/07/06
現在も計算を行い、まとめている最中です。気になること、面白いアイディア、計算に関する質問等がありましたらコメントでもtwitter(@sig_colon)でも、メールでも構いませんのでお知らせください。
計算するまでもない質問の場合はコメントで返信、特に面白そうな場合は、綺麗にまとめて本稿に追加いたします。
2016/02/07
Tech Report ハイスピードカメラによるエアソフトガンの考察
より、ガスガンと電動ガンの銃口付近での空気の流れが見て取れます。
非常に素晴らしく、実際の状況なので信頼できます。15000fpsの高速度カメラだそうです。
ひとつ、気になるのは報告されているBB弾の回転数が私の導き出した値と2倍近く違うことです。
回転数が違うことによって、数値計算結果の回転数以外に影響はありません。ただのホップの強さの目安と見ているので、もしも間違いがあったとしてもホップの強さと回転数との換算が違うだけです。結果には影響しません。
管理人様にお尋ねしたところ、回転数は管理人様自身が導き出したものではなく、考察程度としてみるのがよい、と返答いただきました。残念ながら確証が取れないので回転数の議論はどなたかやっていただけるまで待つことにします。
動画があり、非常に説得力のあるサイトなので、是非ともご覧いただくことをお勧めします。
東京マルイ G36CにおけるノーマルホップとG-HOPの弾道特性
2016/03/22 追)
ガンジニア様のハイスピードカメラによる映像
ホップアップの回転数測定 TM VSR-10 G-SPEC https://t.co/2sVQTTWpM7 @YouTubeさんから
— 石岡@たんそ万歳 (@_Gungineer_) 2016年3月21日
より、本サイト内で表記している回転数にミスがある疑いが濃厚になってきました。
サイト内に「○○回転している」や「○○回転/s」と言う表記があるのはたぶん嘘です。
これから検証していきますのでお待ちください。
2016/07/09追)この問題は解決しました。詳細はBB弾の回転量について(実験との比較)をご覧ください。
2015/07/27
Schrödinger描像、Heisenberg描像、Interaction描像というものがあります。
Schrödinger描像は波動関数による表現方法で、多くの場合で分かりやすい表現なため良く取り入れられます。
ただし、時と場合によってHeisenberg描像の方が分かりやすかったり、Interaction描像の方が最適、というときがあります。
表現方法が違うだけで同じものを表現します。
\(\hat{H}\)が時間依存しない場合、時刻\(t\)での波動関数は初期状態(\(t=0\))の波動関数\(\Psi_S(0)\)を用いて、
\(
\displaystyle \Psi_S(t)=e^{-i\frac{\hat{H}}{\hbar}t}{\Psi_s(0)}\ \ \ \ (1)
\)
と書くことができます。ここで添え字”\(S\)“はS描像であることを強調しています。
\(\displaystyle \hat{U}(t)=e^{-i\frac{\hat{H}}{\hbar}t}\ \ \ (2)\)
と表記されることが多く、時間発展演算子と呼ばれています。
今、(2)の両辺を時間微分すると、\(\hat{U}(t)\)の満たす微分方程式
\(
\displaystyle i\hbar \frac{d\hat{U}(t)}{dt}=\hat{H}\hat{U}(t), \ \ \ \hat{U}(0)=1\ \ \ (3)
\)
が得られます。また、式(3)は実は\(\hat{H}\)が時間依存していても成立します。
この意味は、式(3)が時間発展演算子のより一般的な記述方法であることを意味しています。
今、Schrödinger描像で、とある演算子\(\hat{A}\)の期待値を考えます
(\(\hat{A}_S\)は時間依存してもしなくてもok)。
(例えば\(\hat{A}_S\)は位置空間で、位置演算子だったら\(\hat{x}=x\)、運動量演算子だったら\(\hat{p}=-i\hbar\frac{d}{dx}\)です。)
すると、その期待値を表す関数は時間依存し、時刻\(t\)の\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)は
\(
\begin{align}
\langle\hat{A}\rangle_t
&\displaystyle =\langle{\Psi_S}(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle e^{-i\frac{\hat{H}}{\hbar}t} \Psi_S(0)|\hat{A}_S|e^{-i\frac{\hat{H}}{\hbar}t}\Psi_s(0)\rangle
\end{align}
\)
と書けます。これがSchrödinger描像における演算子の期待値を表現しています。
時刻\(t\)でのHeisenberg描像の波動関数\(\Psi_H(t)\)の定義は
\(
\begin{align}
\Psi_H(t)&=e^{i\frac{\hat{H}}{\hbar}t}\Psi_S(t) \\
&=e^{i\frac{\hat{H}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0) \\
&=\Psi_S(0)
\end{align}
\)
です。
Heisenberg描像で、\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)を考えましょう。
\(
\begin{align}
\langle\hat{A}\rangle_t&=\langle\Psi_S(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_S(t)|e^{-i\frac{\hat{H}}{\hbar}t}e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}e^{i\frac{\hat{H}}{\hbar}t}|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_H(0)|\hat{A}_H(t)|\Psi_H(0)\rangle
\end{align}
\)
すなわち、S描像の演算子\(\hat{A}_S\)との間には、
\(
\hat{A}_H(t)=e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}
\)
という関係があるのです。
では、H描像で演算子\(\hat{A}_H(t)\)の時間依存性はどうなるのでしょう。
上の式を両辺微分して\(i\hbar\)を掛けると、
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{A}_H(t)&=
-\hat{H}e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}
+e^{i\frac{\hat{H}}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}}{\hbar}t}\hat{H} \\
&=-\hat{H}\hat{A}_H(t)+\hat{A}_H(t)\hat{H} \\
i\hbar\frac{d}{dt}\hat{A}_H(t)&=\left[\hat{A}_H(t), \hat{H}\right]
\end{align}
\)
もしも、\(\hat{A}_S\)が時間依存する形だったら
\(
\displaystyle i\hbar\frac{d}{dt}\hat{A}_H(t)=\left[\hat{A}_H(t), \hat{H}\right]+i\hbar \frac{\partial \hat{A}_H(t)}{\partial t}
\)
と書けます。
前提がありまして、系のハミルトニアン\(\hat{H}\)を\(\hat{H}=\hat{H}_0+\hat{V}\)と分けます。
そして、\(\hat{H}_0\)の時間発展は分かっているものとします。
この時、時刻\(t\)でのInteraction描像の波動関数\(\Psi_I(t)\)の定義は
\(
\begin{align}
\Psi_I(t) &= e^{i\frac{\hat{H_0}}{\hbar}t}\Psi_S(t) \\
&(= e^{i\frac{\hat{H_0}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0) )
\end{align}
\)
です。
このInteraction描像の波動関数の意味を簡単に説明すると、
\(\Psi_I(t)\)は、ある時刻で、S描像の波動関数を\(e^{-i\frac{\hat{H}}{\hbar}t}\)に従って時間を進める方向に時間発展させる部分と、\(e^{i\frac{\hat{H}_0}{\hbar}t}\)に従って時間を戻す方向に時間発展させる部分の2つがある、ということです。
詳しくは後ほど述べます。
I描像での演算子\(\hat{A}\)の期待値\(\langle\hat{A}\rangle_t\)はどうなるのでしょう。
\(
\begin{align}
\langle\hat{A}\rangle_t&=\langle\Psi_S(t)|\hat{A}_S|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_S(t)|e^{-i\frac{\hat{H}_0}{\hbar}t}e^{i\frac{\hat{H}_0}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}_0}{\hbar}t}e^{i\frac{\hat{H}_0}{\hbar}t}|\Psi_S(t)\rangle \\
&\displaystyle =\langle\Psi_I(t)|\hat{A}_I(t)|\Psi_I(t)\rangle
\end{align}
\)
と書けます。
すなわち、I描像では演算子が時間依存し、波動関数も時間依存します。
よって、
Interaction描像での演算子\(\hat{A}_I(t)\)の時間依存を記述する方程式と、
Interaction描像での波動関数\(\Psi_I(t)\)の時間依存を記述する方程式
があり、それらを求めてみましょう。
\(
\hat{A}_I(t)=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{A}_S e^{-i\frac{\hat{H}_0}{\hbar}t}
\)
演算子の期待値は上式の通りであり、もしも\(\hat{H}_0\)が時間依存しない場合、Heisenberg描像で\(\hat{H}\to \hat{H}_0\)と置き換えたものと同じ形になります。すなわち、
\(
\displaystyle i\hbar\frac{d}{dt}\hat{A}_I(t)=\left[\hat{A}_I(t), \hat{H}_0\right]
\)
となります。もしも\(\hat{H}_0\)が時間依存する場合は、
\(
\displaystyle i\hbar\frac{d}{dt}\hat{A}_I(t)=\left[\hat{A}_I(t), \hat{H}_0\right]+i\hbar \frac{\partial \hat{A}_I(t)}{\partial t}
\)
では、I描像で波動関数\(\Psi_I(t)\)が満たす運動方程式はどうなるでしょう。
I描像の波動関数の定義式に左から\(e^{-i\frac{\hat{H_0}}{\hbar}t}\)を掛けると、
\(
\Psi_S(t) = e^{-i\frac{\hat{H_0}}{\hbar}t}\Psi_I(t)
\)
であり、これをS描像のSchrödinger方程式に代入します。
\(
\begin{align}
& i\hbar \frac{\partial}{\partial t}\left(e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)\right)
=\hat{H}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
& i\hbar \left[-\frac{i}{\hbar}\hat{H}_0 e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)+e^{-i\frac{\hat{H}_0}{\hbar}t}\frac{\partial \Psi_I(t)}{\partial t}\right]
=\hat{H}_0e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)+\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
& i\hbar e^{-i\frac{\hat{H}_0}{\hbar}t}\frac{\partial \Psi_I(t)}{\partial t}=\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t) \\
\end{align}
\)
左から\(e^{i\frac{\hat{H}_0}{\hbar}t}\)を作用させると、
\(
\displaystyle i\hbar \frac{\partial \Psi_I(t)}{\partial t}=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}\Psi_I(t)
\)
ここで、Interaction描像の演算子\(\hat{H}_I(t)\)を
\(
\displaystyle \hat{H}_I(t)=e^{i\frac{\hat{H}_0}{\hbar}t}\hat{V}e^{-i\frac{\hat{H}_0}{\hbar}t}
\)
と置くと、波動関数\(\Psi_I(t)\)が満たす運動方程式
\(
\displaystyle i\hbar \frac{\partial \Psi_I(t)}{\partial t}=\hat{H}_I(t)\Psi_I(t)
\)
が得られます。
さて、定義が終わったところで、Heisenberg描像とInteraction描像の意味を見てみましょう。
簡単にそれぞれの描像を説明すると、
Heisenberg描像:量子-古典対応を成す
Interaction描像:既に分かっている部分を取り除く
という特徴があります。
まずはHeisenberg描像から。
Heisenberg描像でHeisenberg描像の演算子\(\hat{A}_H(t)\)の時間発展を記述する運動方程式は
\(
i\hbar\frac{d}{dt}\hat{A}_H(t)=\left[\hat{A}_H(t), \hat{H}\right] \cdots(A)
\)
です。
今、\(\hat{A}_H(t)\)が位置演算子\(\hat{q}\)と運動量演算子\(\hat{p}\)によって表記されていると考えます。
この時、Schrödinger描像で、それぞれの演算子はハミルトニアンと
\(
\begin{align}
\left[\hat{q}_S,\hat{H}_S\right] &= i\hbar \frac{\hat{p}_S}{m} \\
\left[\hat{p}_S,\hat{H}_S\right] &= -i\hbar \frac{\partial}{\partial \hat{q}_S}\hat{H}_S
\end{align}
\)
という関係があります。
Heisenberg描像でSchrödinger描像のハミルトニアンがどう記述されるのかを考えてみると、
\(
\begin{align}
\hat{H}_S &= \frac{\hat{p}_S^2}{2m}+\hat{V}_S \\
&= \frac{1}{2m}e^{-i\frac{\hat{H}_S}{\hbar}t}\hat{p}_H^2 e^{i\frac{\hat{H}_S}{\hbar}t}+e^{-i\frac{\hat{H}_S}{\hbar}t}\hat{V}_H^2 e^{i\frac{\hat{H}_S}{\hbar}t} \\
&= e^{-i\frac{\hat{H}_S}{\hbar}t}\left( \frac{\hat{p}_H^2}{2m}+\hat{V}_H\right) e^{i\frac{\hat{H}_S}{\hbar}t} \\
\hat{H}_H&= e^{i\frac{\hat{H}_S}{\hbar}t}\hat{H}_S e^{-i\frac{\hat{H}_S}{\hbar}t} \\
&=\hat{H}_S
\end{align}
\)
となり、結局
\(
\hat{H}_S=\hat{H}_H
\)
であることが導かれます。
Heisenberg描像での位置演算子\(\hat{q}\)と運動量演算子\(\hat{p}\)の交換関係は
\(
\begin{align}
\left[\hat{q}_H,\hat{H}_H\right] &= i\hbar \frac{\hat{p}_H}{m} \\
\left[\hat{p}_H,\hat{H}_H\right] &= -i\hbar \frac{\partial}{\partial \hat{q}_H}\hat{H}_H \\
\end{align}
\)
であることが導けるため、\(\hat{q}_H\)と\(\hat{p}_H\)に関して、運動方程式に代入して
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{p}_H(t)&=\left[\hat{p}_H(t), \hat{H}_H\right] \\
&= -i\hbar \frac{\partial}{\partial \hat{q}_H}\hat{H}_H \\
\frac{d}{dt}\hat{p}_H(t)&=-\frac{\partial}{\partial \hat{q}_H}\hat{H}_H
\end{align}
\)
であり、
\(
\begin{align}
i\hbar\frac{d}{dt}\hat{q}_H(t)&=\left[\hat{q}_H(t), \hat{H}_H\right] \\
&= i\hbar \frac{\hat{p}_H}{m} \\
\frac{d}{dt}\hat{q}_H(t)&=\frac{\partial}{\partial \hat{p}_H}\hat{H}_H
\end{align}
\)
となります。
この二つの式は、古典力学のハミルトンの運動方程式に酷似していますよね。ここからHeisenberg描像が量子-古典対応を成す、という所以になるわけです。
注意として、Heisenberg描像は、量子-古典対応を成しますが、演算子それ自身を測定することなどできないのです。あくまで期待値と対応するだけです。
また、Heisenberg描像は古典力学への回帰を見出し、エーレンファストの定理と関連します。
続いて相互作用描像です。
系のハミルトニアン\(\hat{H}\)を\(\hat{H}=\hat{H}_0+\hat{V}\)と分けます。
そして、\(\hat{H}_0\)の時間発展は分かっている時、Interaction描像の波動関数\(\Psi_I(t)\)は
\(
\begin{align}
\Psi_I(t) = e^{i\frac{\hat{H_0}}{\hbar}t}e^{-i\frac{\hat{H}}{\hbar}t}\Psi_S(0)
\end{align}
\)
でした。じっくり見ていきましょう。
例を考えます。
\(
\displaystyle \hat{H}=\hat{H}_0+V(x)=-\frac{\hbar^2}{2m}\nabla^2+V(x)
\)
で、ポテンシャル\(V(x)\)が単調減少で図のような山なりの波形をしている場合を考えます。
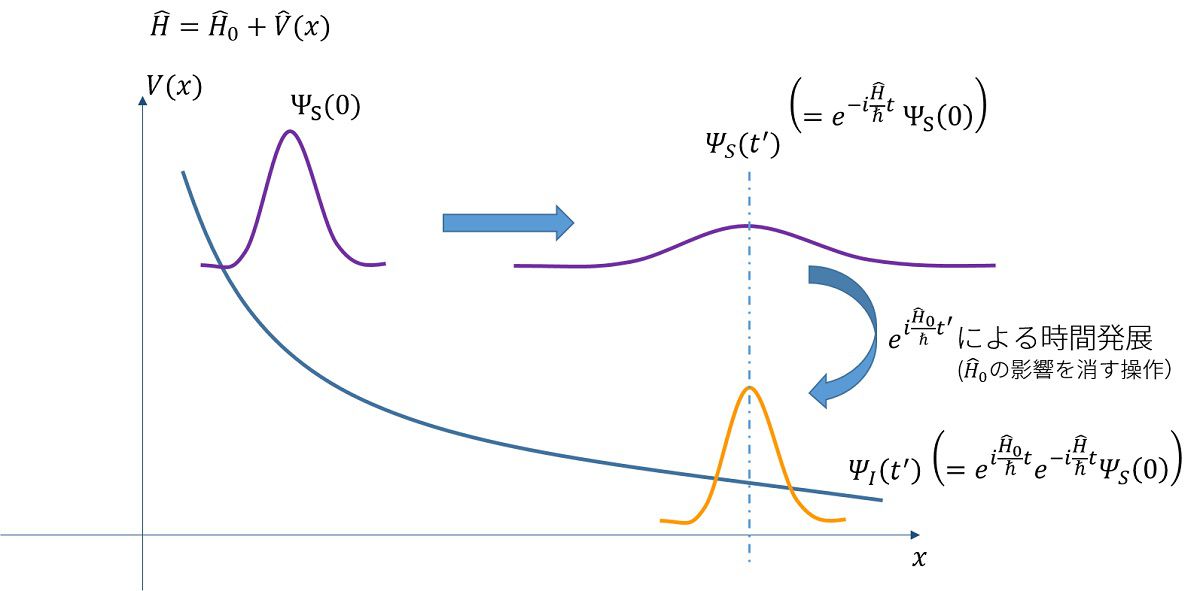
初期状態\(\Psi_S(0)\)があったとすると時間経過すると、その波動関数の形は広がりながら右へ移動します。
Interaction描像では、この、広がる、という動きと、右へ移動する、という動きが合わさったと考えます。
広がる動きは、ポテンシャルが無いときの波束の動きです。ポテンシャルがない時、右に動くことはしません。
右への動きは、ポテンシャルしか無いときの波束の動きです。質点を考えれば、ポテンシャルの山を転がり、右へ動きます。
Interaction描像の波動関数\(\Psi_I(t)\)は既に分かっている広がる動き(\(\hat{H}_0=-\frac{\hbar^2}{2m}\nabla^2\)の部分)を取り除き、波束が右に動く描像(\(V(x)\)の部分)だけを切り抜くのです。
言葉で言えば、Interaction描像は、
\(t’\)秒後の\(I\)描像における波動関数は、\(t’\)秒後の\(S\)描像における波動関数に対して、\(t’\)秒間の\(\hat{H}_0\)による逆方向の時間発展を行えばよい、ということです。
あくまでもイメージなので、細かな議論はご了承を。
David J. Tannor著、山下晃一ほか訳『入門 量子ダイナミクス(上)』(2011), p.231~236